Topological properties of Sb(111)surface: A first-principles study

Shuangxi Wang(王雙喜) and Ping Zhang(張平)

1Department of Materials Science and Engineering,China University of Petroleum,Beijing 102249,China

2Institute of Applied Physics and Computational Mathematics,Beijing 100088,China

3Center for Applied Physics and Technology,Peking University,Beijing 100871,China

Keywords: first-principles study,antimony,topological states

1. Introduction

A new state of quantum matter, topological insulator(TI), has received amount of attention in condensed matter physics.[1,2]The realization of TI HgTe both from theoretical prediction and experimental observation,[3,4]opens up opportunities for its potential application in semiconductor spintronics. It is believed that the quantum spin Hall effect as well as the time-reversal symmetry plays an important role in the new material,protecting the system from being disturbed by small perturbation caused by defects. This urges people to desire for more other promising materials,such as the Bi-based alloy Bi1-xSbx,and layered compound Bi2X3(X=Se,Te).[5-8]Recently, due to its novel topological properties, the semimetallic antimony(Sb)has become the ideal proto-type system for studying TI,thus has been investigated both theoretically and experimentally.[9-15]

Theoretically,it has been proposed that the spin-orbit interaction (SOI) gives rise to the inverted structures between the valance and conduction band, and hence nontrivial gapless edge states emerge on the surface of Tls.[3]These studies revealed that the SOI plays a dominant role in characterizing the surface states of Sb,[9]and the properties of surface states depend on the thickness of this kind of two-dimensional(2D) material.[14,15]Experimental researches identified that the spin-split surface bands of Sb within its bulk band gap are connected to the conduction band and valence band.[9,10]Moreover, the topologically nontrivial Sb thin films exhibit novel properties and provide a promising playground for spintronic applications in low dimensions, such as device design and integration.[11]

Nevertheless,there exist still many unanswered questions about the electronic structures of Sb. For Sb(111) surface, it is desirable to identify the layer-dependence of the topological states of Sb thin film,and the modulating of the surface properties by impurities with or without magnetic moment.[16,17]Moreover,the understanding of properties of Sb(111)surface can greatly facilitate the research of interaction between adsorbates and Sb(111) surface.[12]Therefore, it would be instructive to explore the electronic structures of Sb to make a thorough comprehension about the topological properties.

The density functional theory (DFT) calculations based on first-principles method have proved to be an effective approach for studying the structural and electronic properties of materials including TIs.[18-23]In the present work, we study the properties of Sb(111) surface by performing firstprinciples calculations. The bulk band structure of Sb is presented to reveal the domination of SOI for topological properties of Sb. For the stoichiometric Sb(111) surface, we investigate the layer-dependence of the surface states of Sb thin film.Moreover,we calculate the surface properties of Sb when impurities are introduced, including nonmagnetic Bi and 3d transition metal ion Mn. The reason why we choose Bi as the doped impurity is that bismuth-antimony alloy has been investigated as a topological insulator, and it has potential application in developing next-generation quantum computing devices.[24-26]If the impurity carries a magnetic moment,the time-reversal symmetry is explicitly broken, and a local energy gap will be opened up near the Dirac point.[17]Moreover, transition metal element Mn doped HgTe[27]has been theoretically predicted to show the quantum anomalous Hall(QAH)effect. Hence Mn exhibits unique magnetic properties involved in the TI materials. While up to now further relevant study about Mn doped TIs is still lacking, we choose Mn as the doped magnetic impurity to have a direct and intuitional sight into it.

This paper is outlined as follows. Firstly,the calculation method employed in our works is briefly introduced. Secondly,we present and discuss our results for the surface properties of Sb(111). Finally,we provide a summary.

2. Calculation method

The calculations were performed by using the density functional theory,as implemented in the Viennaab-initiosimulation package (VASP).[28]The Perdew-Burke-Ernzerhof(PBE)[29]parametrization of the generalized gradient approximation(GGA)was used for the exchange-correlation energy,and the projector-augmented wave potentials[30]were employed to describe the electron-ion interaction. Here the Sb 5s and 5p electrons were treated as valence electrons. The planewave cutoff energy was set to be 400 eV, with a smearing parameter[31]of 0.1 eV.The SOI was also included throughout the calculations.

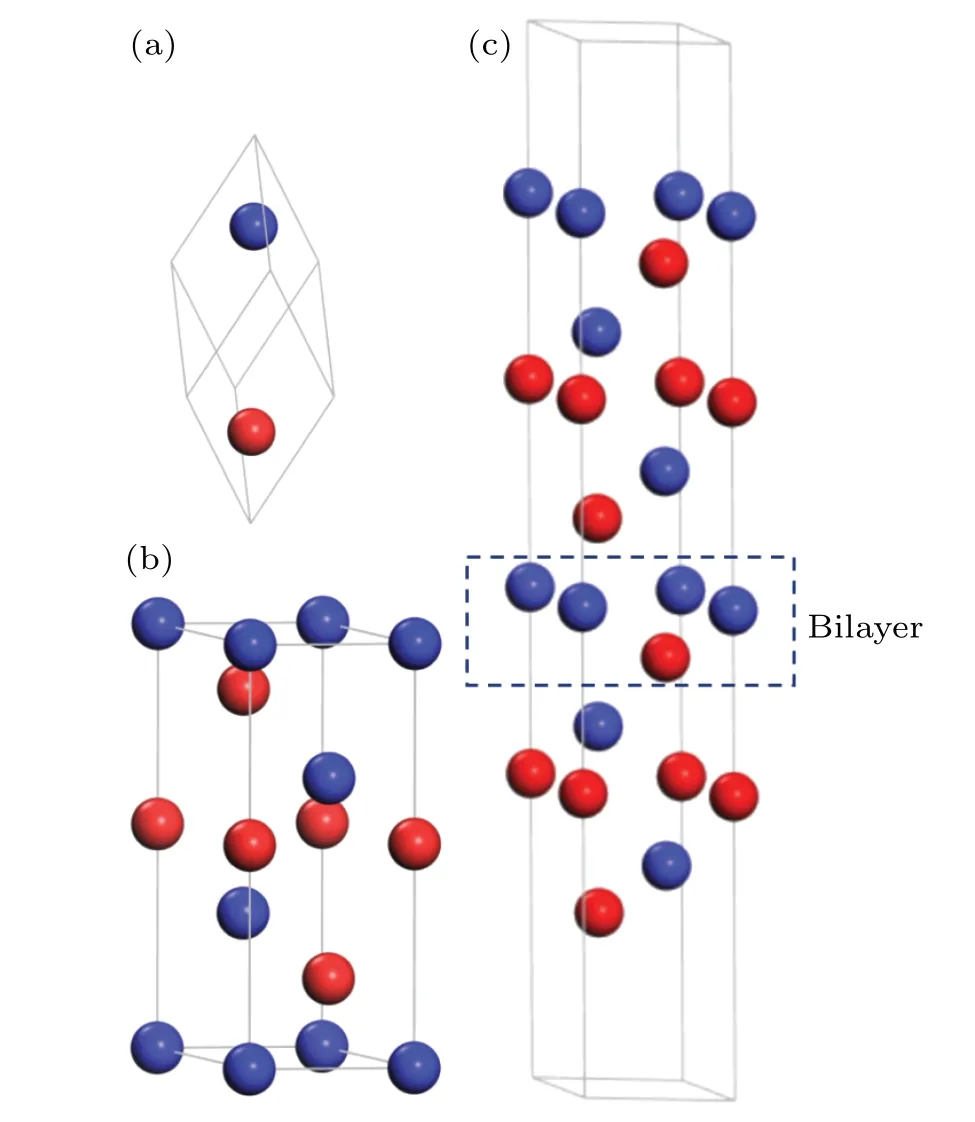
Fig. 1. Atomic structure of bulk Sb and Sb(111) surface. The nonequivalent antimony atoms are represented by blue and red balls separatively: (a)primitive cell of bulk Sb,(b)hexagonal unit cell of bulk Sb and(c)slab model of Sb(111)surface.

The crystal structure of Sb is rhombohedral with the space groupD53d(Rˉ3m),with two non-equivalent Sb atoms in the trigonal primitive cell (see Fig. 1(a)). We can also present it in terms of a hexagonally arranged layer structure, as shown in Fig. 1(b). The hexagonal unit cell can be regarded as three sets of bilayers,where each bilayer consists of two Sb atoms.Structurally,bilayers in Sb form a stable unit with strong intrabilayer bonds,while the interbilayer bonding is much weaker.To identify nonequivalent atoms in the slab structure,different layers of Sb are labeled with different colors in the hexagonal cell. The Sb(111) surface is modeled by a slab composing of several (1-6) bilayers (BLs) and a vacuum region of 20 °A as shown in Fig. 1(c). Integration over the Brillouin zone was done by using a 21×21×1 Monkhorst-Packk-point mesh[32]for thep(1×1)surface,in which each monolayer contains one Sb atom; for thep(3×3)surface, in which each monolayer contains nine Sb atoms, 7×7×1 grid points are used. The structures of slabs were fully optimized until the absolute value of the atomic force on each atom was below 0.02 eV/°A. The computed lattice constants of rhombohedral Sb area=4.39 °A andc=11.43 °A, which are in agreement with the experimental dataa=4.3007 °A andc=11.222 °A.[33]

3. Results and discussion

It has been proposed that Sb is a promising TI by calculating its Z2invariantν(=1)from the knowledge of the parity of the occupied Bloch wave function at the time-reversal invariantΓpoint in the Brillouin zone.[24]This means that the SOI dominates the electronic nature of Sb,and one can understand it from the band structure (see Fig. 2). It is clear that the band gap is very small without SOI. While as the SOI is taken into consideration,the band gap is enlarged up to about 0.24 eV. We notice that the GGA calculations generally tend to underestimate the band gap for nonmetals.[34]Nevertheless,previous study with standard DFT correctly described the band properties of TIs, such as Bi2Se3[5,35]and Bi2Te3.[6]Therefore, our calculations still yield physically reasonable results about the general properties of band energy of Sb. Moreover,because of its topological electronic nature,we can expect the existence of gapless surface states. Therefore, in the following we will focus our attention on the properties of Sb(111)surface.

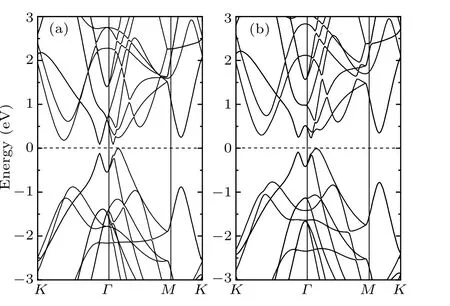
Fig. 2. Bulk band structure without SOI (a) and with SOI (b). The energy zero is set at the valence band maximum.

Generally speaking,the surface topological properties are sensitive to the thickness of the TI thin film. For thinner film,the coupling between the top and bottom surfaces is strong enough to open up a whole insulating gap. With increasing thickness,the inter-surface coupling becomes weaker and the topological features will be recovered. This is the same case for Sb(111)surface. As illustrated in Fig.3,we show the evolution of band structure of Sb films with the thickness from the single BL to six BLs. In a single BL film,the Sb electronic states (mainly from 5p orbital) split into two parts forming a gap around the Fermi level.The gap is as large as about 0.9 eV,implying the strong coupling between two surfaces. In the case of two BLs films,the splitting of 5p states decrease with the decline of the coupling, leading to a semimetallic electronic structure. Obviously, the topological features start to appear in the three BLs case,where a non-trivial helical edge state(ν0=1)below the Fermi level atΓpoint can be identified. This helical state is consist of two surface states degenerated atΓpoint but separated in energy elsewhere by SOI.[11]Nevertheless,it is noticeable that for the case of four BLs and five BLs films,the gaps are opened up again atΓpoint. This can be attributed to the inverse asymmetry of the films with four and five BLs. While the topological states should be recovered when the number of BLs of the film is multiples of three, which conserves the inverse symmetry. As expected,it can be seen that the topological states are recovered for six BLs,which are consistent with the previous computational and experimental results.[15]The double degenerate Sb(111) surface states contain a single Dirac cone at theΓpoint,which is robust and topologically protected by time-reversal symmetry.The Dirac point is about 0.16 eV below the Fermi level,within the bulk band gap. Compared with the experimental value of 0.23 eV,[2]the difference may arise from the subsurface defects observed in the experiment.

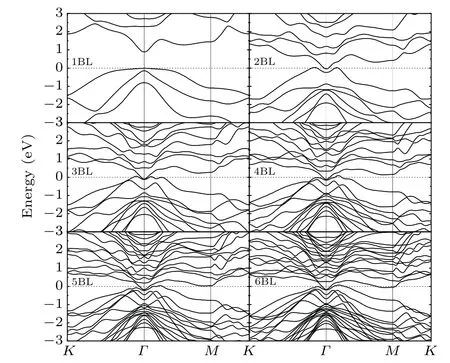
Fig. 3. Surface band structure with one to six bilayer thickness. The energy zero is set at the valence band maximum.

Various impurities may have different impact on the degeneracy and topological properties of Sb energy bands,which will be illustrated in the following discussions based on the six BLs film. It has been shown that the alloy Bi1-xSbxis a 3D TI.[24,25,36]Here it would be interesting to investigate the surface state properties of reduced Sb(111) surface with the existence of Bi as a nonmagnetic impurity. Moreover, as a comparison,a magnetic impurity(Mn atom)is also taken into consideration. During the calculations, thep(3×3) surface is adopted,and impurities are symmetrically introduced on both sides of the slab.

We found that the substitutional Bi or Mn atoms take the position of one subsurface Sb2 atoms, and the adsorbed Mn atoms are found to be energetically stable at the hcp sites above Sb(111) surfaces. As depicted in the upper panels of Fig.4,the introduced Bi is about 0.06 °A lower than the adjacent Sb2 atom,and causes only slightly distortion of surrounding atoms. The substitutional Mn atom is 0.56 °A lower than the adjecent Sb2 atom,and causes the move of the surface Sb1 atom (0.31 °A downwards). The adsorbed Mn atom is higher than the outmost surface by 0.56 °A, and causes only slightly move of the surface atoms.

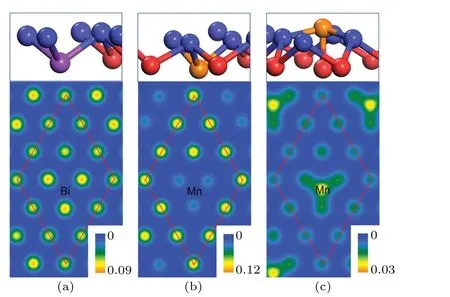
Fig. 4. Structures of Sb(111) surfaces with impurities (upper panels)and surface charge density distributions (lower panels, in e/°A3) at the height of 2.0 °A above the Sb(111) surface: (a) Bi-substitutional, (b)Mn-substitutional and(c)Mn-adsorbed. The Bi and Mn atoms are represented by purple and orange balls,respectively.

To explore the bonding information between impurities and surface, we calculated the charge density distributions of Sb(111)surfaces with impurities. As shown in Fig.4,the localized three-fold symmetric features can be identified from all of the surfaces,especially for the Mn-doped ones. For the Bisubstitutional surface, only tiny difference exists between the region above the Bi atom and others,and this can be attributed to that Bi and Sb belong to the same chemical group and possess the same number of valence electrons. As a result, the Bi-doped Sb(111) surface may maintain the topological features,which will be illustrated later by the band structure. For the Mn-doped surfaces, however, more evident different features can be observed. It is noticeable that the charge distribution is strongly depleted at the position just above the substitutional Mn atom,while the adsorbed Mn atom can be identified clearly by the charge accumulation. Keeping in mind the magnetism of Mn atom,we will see that the magnetic impurity can have significant effect on the surface states of Sb(111)surface.

The band structure of Bi-doped Sb(111) surface is presented in Fig. 5(b). For comparison, in Fig. 5 we show the Sb bulk band structure projected onto the surface Brillouin zone, and also in next series of surface band structures. The band structure of stoichiometricp(3×3) Sb(111) surface is also shown in Fig.5(a). It is clear that the topological surface state remains to be robust despite of the existence of Bi impurity, and the Dirac point of this reduced surface almost stays at the same position as that of the stoichiometric surface,i.e.,residing in the bulk valence band gap.This can be attributed to the following reasons. (1)The time-reversal symmetry stands against nonmagnetic impurities. (2) The energy bands of Bidoped system remain degenerate thus keep gapless.Moreover,from the PDOS of Bi we determined that the doped Bi atom contributes little to the band structure near the Fermi level and the Dirac point, thus the topological features of Sb keep robust,which also consists with the fact that the alloy Bi1-xSbxis a 3D TI inherited from Sb.[24]

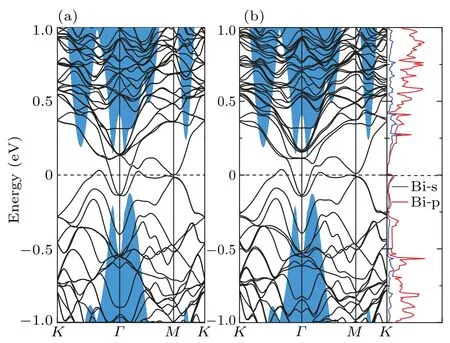
Fig.5. The band structure of clean(a)and Bi substitutional(b)Sb(111)surface. Blue shaded areas correspond to the Sb bulk band structure projected onto the surface Brillouin zone.

For magnetic Mn-doped Sb(111) surface, we found that the magnetic impurities can obviously lift the degeneracy protected by the time-reversal symmetry. For clarity,here we plot the lifted band structures of Mn-substitutional and adsorbed Sb(111) surfaces dividedly in Figs. 6 and 7, labeled by spinup and spin-down,respectively. It can be seen that both of the magnetic impurities eliminate the Dirac point by opening up a gap atΓpoint, corresponding to the position of band gap of the bulk valence band. As depicted by the PDOS (Figs. 6(c)and 7(c)), compared with the doped Bi atom, the magnetic d orbital of Mn atom contributes much to the states near the Dirac point, hence clearly breaks the time-reversal symmetry. As expected,[17]a ferromagnetic ground state is formed on the TI surface by the introduced magnetic Mn impurity. As to the aforementioned QAH effect appearing in TIs, the Mndoped HgTe[27]and Cr(Fe)-doped Bi2Se3[37]exhibit insulating magnetic state, and QAH effect emerges. However, we can see from the PDOS that the metallic states are obtained for Mn-doped Sb(111)surface,similar to that for Ti(V)-doped Bi2Se3,[37]which is topologically trivial.

Fig. 6. The band structure of Mn-substitutional Sb(111) surface: (a)spin-up, (b) spin-down and (c) the PDOS of the Mn atomic d-bands.Blue shaded areas correspond to the Sb bulk band structure projected onto the surface Brillouin zone.

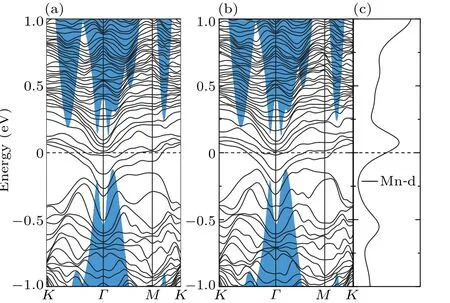
Fig. 7. The band structure of Mn-adsorbed Sb(111) surface: (a) spinup, (b) spin-down and (c) the PDOS of the Mn atomic d-bands. Blue shaded areas correspond to the Sb bulk band structure projected onto the surface Brillouin zone.

4. Conclusion

In summary,we used the first-principles method to study the topological properties of Sb(111) surface. We found that the stoichiometric Sb(111)surface possesses single Dirac point protected by the time-reversal symmetry and inverse symmetry. And the topological states are layer dependent and keep robust for six bilayers film. Moreover, we revealed that the non-trivial topological states stand for non-magnetic substitutional Bi, while the substitutional or adsorbed magnetic Mn atom can obviously destroy the topological states by eliminating the Dirac point. The present work may contribute to the further study in topological insulator.