Optimized quantum singular value thresholding algorithm based on a hybrid quantum computer

Yangyang Ge(葛陽(yáng)陽(yáng)), Zhimin Wang(王治旻), Wen Zheng(鄭文), Yu Zhang(張鈺), Xiangmin Yu(喻祥敏),Renjie Kang(康人杰), Wei Xin(辛蔚), Dong Lan(蘭棟), Jie Zhao(趙杰),Xinsheng Tan(譚新生), Shaoxiong Li(李邵雄), and Yang Yu(于揚(yáng))

National Laboratory of Solid State Microstructures,School of Physics,Nanjing University,Nanjing 210093,China

Keywords: singular value thresholding algorithm,hybrid quantum computation

1. Introduction

Quantum computation,[1]since its quantum advantage over conventional one, has been an attractive and inspiring field for decades. Many physical platforms, such as trapped ions,[2-4]nuclear magnetic resonance,[5,6]photons,[7-9]and solid state superconducting devices[10-13]have been deeply explored to find a viable way to building a quantum computer.While the major effort has been put on the quantum operations on two-state quantum variables (being known as qubits), for quantum systems, there exist both DVs and CVs. Resources like position, momentum, and quadrature amplitudes of the electromagnetic field are suitable candidates for continuous variables. The quantum version of a CV mode (qumode)[14]can be comparable to a qubit. The quantum information processing can take advantage of both DVs and CVs.[15,16]Its superiority has been shown in applications like quantum float computing[17]and quantum phase estimation.[1,14]

In this paper, by using both DVs and CVs, we propose a hybrid quantum algorithm for singular value thresholding(SVT)to efficiently save physical resources while with quantum speed-up. SVT is a core module in many important applications like computer vision and machine learning. Specifically,the SVT algorithm has been applied to solve many nuclear norm minimizing (NNM)-based problems, such as matrix completion, matrix denoising, and principle component analysis (PCA).[18-20]The processes of SVT are the main computational cost for those applications.

Since the superiority of quantum computer,many remarkable quantum machine learning[21]algorithms have been proposed. A QSVT algorithm[22,23]has been developed that can execute the SVT operator exponentially faster than its classical counterparts. The algorithm for QSVT consists of three main parts: quantum phase estimation, Newton iteration, and controlled rotation. All the three parts require indispensable ancillary qubits as registers for quantum float computing. Depend on the desired precision, the demand for the number of ancillary qubits could be large and a grand challenge for realization on near-term intermediate-scale quantum computers.This motivates us to resort to hybrid quantum computation and work out a more efficient approach to economize the quantum resources.

Vectors of classical data are better encoded in quantum states of qubit systems, as each component of a vector now becomes the corresponding amplitude directly. However, the all-qubit approach demands for lots of ancillary qubits as registers in its several main parts, which can be more efficiently performed with CVs-based operations. Given the above two considerations, it naturally calls for a hybrid quantum computing approach that exploits both the advantages of qubits and qumodes,as would be explored in this paper.

In our proposed hybrid QSVT algorithm,singular values are encoded into the CVs and singular value transformation can be implemented by hybrid controlled unitary transformations. In contrast to the all-qubit scheme that requires redundant qubits and complicated circuits, our hybrid scheme consumes only a limited amount of qubits and qumodes and significantly reduces the complexity of the circuit. Our complexity analysis shows that the hybrid scheme depresses the order of runtime comparing the all-qubit approach.

The remainder of this paper is organized as follows: We give a brief review of the all-qubit QSVT algorithm in Section 2 and propose our modified hybrid QSVT algorithm in Section 3. Section 4 analyzes the complexity, success probability,and fidelity. We present our conclusions in Section 5.

2. All-qubit QSVT algorithm

In this section, we first briefly review the procedures of the all-qubit QSVT algorithm. And then design a modified hybrid QSVT algorithm(HQSVT).

The QSVT algorithm is based on the singular value decomposition (SVD).[18]Given a low rank matrixA ∈RM×Nwith rankR ≤min(M,N),Ai,jrepresents the elements of thei-th row andj-th column of matrixA. The singular value decomposition (SVD) ofAis a factorizationA=UΣV?=∑Rk=1σkukvk,whereσkare called singular values ofAanduk,vkrepresent left and right singular vectors respectively. In the QSVT algorithm,suppose the matrixAis the input,the output takes the form of ∑rk=1(σk-τ)+ukvkwherer ≤Randτis a threshold. Here(σk-τ)+=max(σk-τ,0).

Figure 1 shows the circuit representation of the QSVT algorithm.The algorithm is based on the HHL algorithm[24]and can be decomposed into five parts. The state evolution corresponds to each part of the circuit is represented in Fig. 2.In initialization, by using quantum random access memory(qRAM),[25-27]the elements of the input matrixAare stored in registerB.In the first part,the algorithm performs the quantum phase estimation ?UPEand stores the singular value information in registerC. The second part contains an unitary operation ?Uσ,τwhich converts the eigenvalues|σ2k〉stored in registerCto the intermediate result|yk〉stored in the registerL, whereyk=(1-τ/σk)+∈[0,1). Then|yk〉stored in registerLcontaining the information of eigenvalues is assigned to the amplitude of the auxiliary qubit through rotation transformation in the third step. In the fourth part,an unitary transformation ?U?is used to eliminate the unwanted registers. Eventually,the measurement is performed on the auxiliary qubit and registerBcollapses to the target quantum state. The algorithm outputs the state|ψS〉close to the desired result.

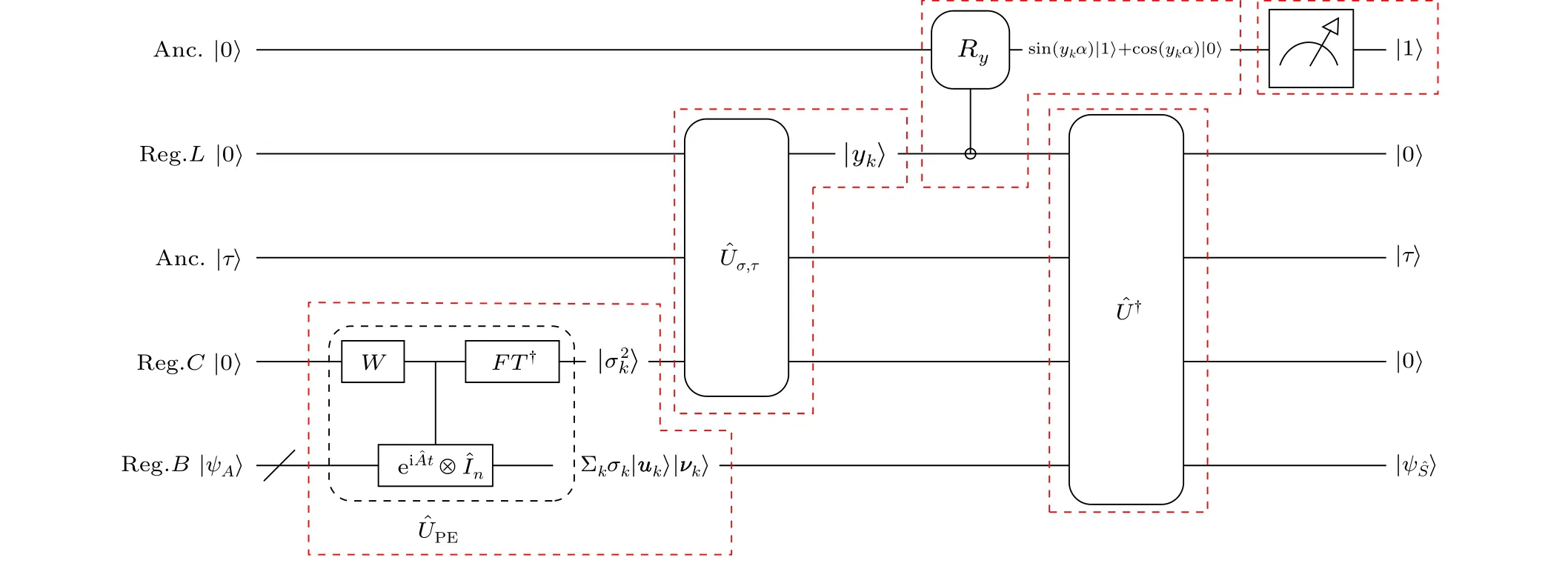
Fig.1. Quantum circuit of the all-qubit QSVT algorithm. The circuit is divided into 5 parts by the red dashed box. The bottom wire with‘/’represents a group of qubits.

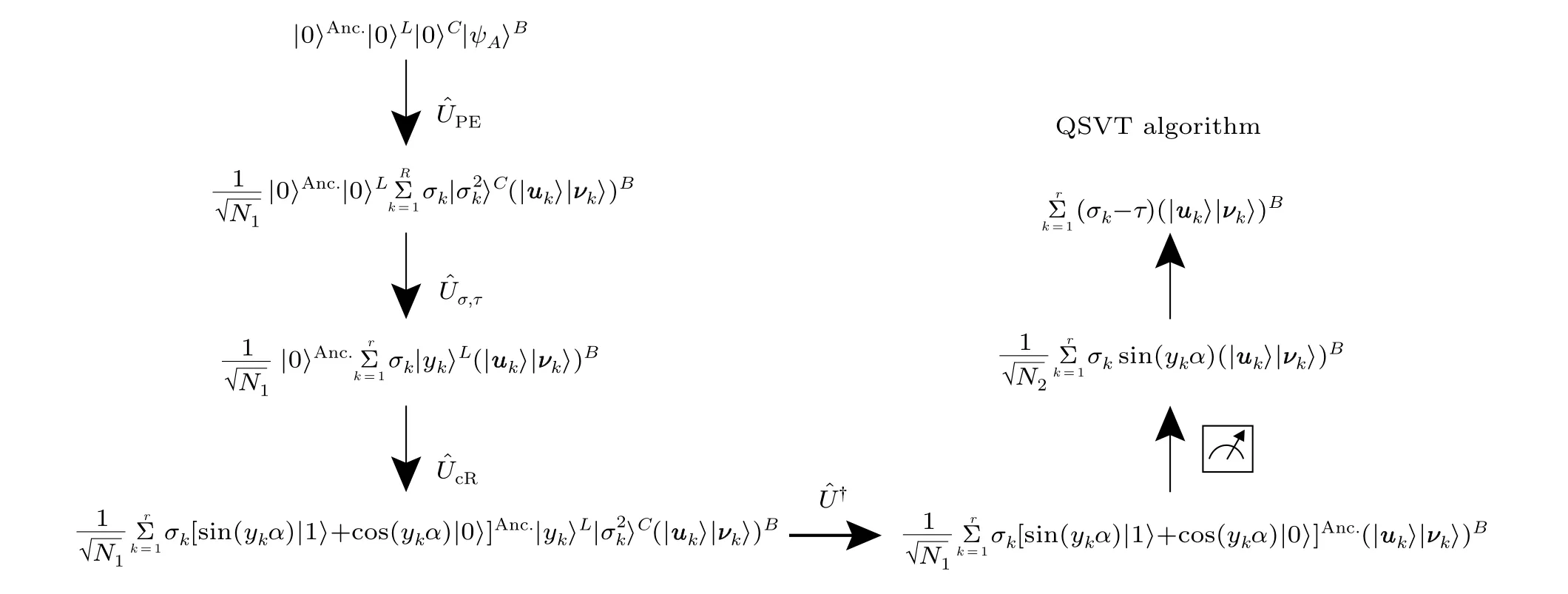
Fig.2. Entire state evolution corresponding to procedures of the all-qubit QSVT algorithm. The ancillary state|τ〉is omitted because it remains the same during the evolution of the quantum circuit.

3. Hybrid QSVT algorithm

In this section, we elaborate our modified hybrid QSVT algorithm(HQSVT).For the all-qubit QSVT algorithm,it can be decomposed into several main procedures,including quantum phase estimation, Newton iteration, and controlled rotation. We keep these procedures and reconstruct them with hybrid operations or CVs-based operations.

The first reconstructed procedure of our algorithm is quantum phase estimation, where a hybrid operator ?U=e-iATA?Pis constructed to extract the singular values and register them into the qumode. As shown in Eq.(1),

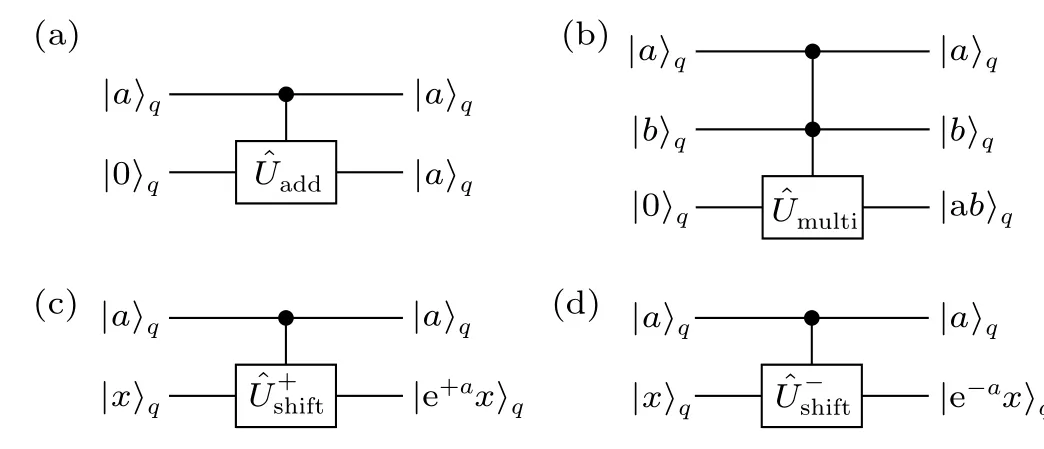
Fig. 3. Addition, multiplication, and shift operations based on CVs. Here we use subscript q to indicate that the register is a qumode. (a)The addition operation needs two qumodes with the first qumode determining the quantity of addition and the second qumode taking the form of output. (b)The multiplication operator multiplies the values stored in the first two qumodes and register the result in the third qumode. Both panels(c)and(d)are shift operations. Here panel(c)takes Xx →e+aXx:U+shift “stretches”Xx and panel(d)takes Xx →e-aXx:Ushift “squeezes”Xx.

The next part is the controlled rotation.Here we introduce a hybrid rotation operation shown in Fig.4,which extracts theykstored in registerLto the amplitude of the ancilla qubit.The operator e-i?X??σxtis essentially hybrid.It extracts theykstored in the qumode and then assignsykto the amplitude of an auxiliary qubit,instead of extractingykfrom registerLconsisting of qubits:

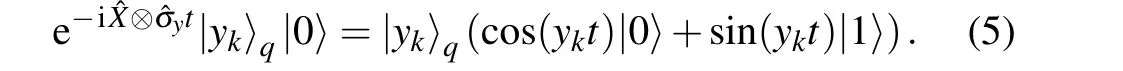
Fig.4. Circuit of the controlled rotation operation. In this hybrid operation,the value stored in the qumode is assigned to the amplitude of the auxiliary qubit.

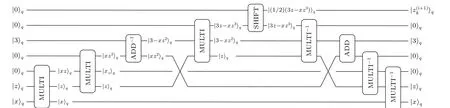
Fig. 5. Quantum circuit of one Newton iteration for computing =g=(1/2)（3z-xz3）. The iteration is composed of CVs-based quantum operations.

The other procedures are consist with the all-qubit scheme. We perform an operator ?U?and then do the measurement on the auxiliary qubit.

The overall procedures of our HQSVT algorithm is organized as the following steps.

Step 1 Initialization. The matrixAis loaded as state|ψA〉via qRAM:

4. Algorithm analysis

In this section, we first analyze the space consumption and time complexity of our algorithm and then briefly describe the success probability and fidelity.

4.1. Complexity

To begin with,we focus on the space consumption of our algorithm. In the hybrid quantum phase estimation,registerBstoring|ψA〉takes up most space in our algorithm.The number of qubits in registerBisb=O[log(MN)].In addition,we need a few(8 to be precise)qumodes with squeezing factor[14]ε-1for the desired precisionεin the computation of ?UPE, ?Uσ,τ,and ?Uc,R. In contrast,the register consisting of qubits requiresO[log(ε-1)] qubits to register a floating point value. Therefore, we need totallyO[log(MN)] qubits andO(1) qumodes in our hybrid scheme, which is significantly less than the allqubit QSVT algorithm requiringO[log(MN/ε)] qubits. We reduce the number of qubits by replacing the registers widely used in ?UPE, ?Uσ,τ,and ?Uc,Rwith qumodes.

We now turn to the runtime analysis. Our hybrid quantum phase estimation is much simplified,only a single operation ?U=eiH?Pon|ψA〉|0〉qis performed,and the singular values are registered into the qumode. However, in the all-qubit scheme, performing quantum Fourier transformation (QFT)onNqubits takes the order ofN2quantum operations.[1]The number of operations in the computation of ?Uσ,τis a low degree polynomial in the quantity of qumodes. Since the space of qumodes isO(1), ?Uσ,τtakes the runtime ofO(1). The next operation ?Uc,Ris another single gate. Therefore,the total number of operation in our hybrid approach isO(1). While in the all-qubit QSVT algorithm, the number of operation isO[poly(log(1/ε))].

To summarize,our proposed HQSVT algorithm requiresO[log(MN)] qubits andO(1) qumodes, and the runtime isO(1).It is noted that we did not take the runtime for the preparation of intial state|ψA〉and the time used to construct ?UPEinto account. It costs timeO[log(MN)]via qRAM to prepare state|ψA〉. For desired precisionε, it requiresO(ε-1)copies of density matrixATA,where each copy of density matrixATAcan be obtained from|ψA〉inO[log(MN)]by qRAM.Thus the total runtime scales asO[ε-1log(MN)]and our runtime optimization is limited.

4.2. The success probability and fidelity

We now analyze the probability of obtaining the final result and the fidelity between the ideal and actual results in the same way as the all-qubit approach.

In the first place,the probability of obtaining the final result is calculated as follows:

andF(α)≈1.

5. Conclusion

In this paper, we utilized the advantages of qubits and qumodes in a balanced way and proposed an HQSVT algorithm based on the all-qubit QSVT algorithm. It enables the hybrid quantum computer to solve many NNM-based problems. We decomposed our algorithm into several key subroutines and further investigated the construction of each subroutine through hybrid systems composed of qubits and qumodes.Then we analyzed the space-time complexity of our algorithm, which shows that our algorithm requiresO[log(MN)]qubits andO(1) qumodes, and its runtime isO(1), therefore it is an optimization of the all-qubit QSVT algorithm. In order to register the singular values with the same precision as the all-qubit approach, we take qumodes with squeezing factorε-1for the desired precisionε, so that our algorithm has the same success probability of obtaining the final result and the fidelity between the ideal and actual outputs. It is worth mentioning that our optimization method is not limited to the QSVT.The proposed method can be applied to other quantum phase estimation-based algorithms,such as quantum principal component analysis and quantum linear regression.

Acknowledgments

Project supported by the Key Research and Development Program of Guangdong Province, China (Grant No. 2018B030326001) and the National Natural Science Foundation of China (Grant Nos. 61521001, 12074179, and 11890704).