Diffusion of a chemically active colloidal particle in composite channels
Xin Lou(婁辛) Rui Liu(劉銳) Ke Chen(陳科) Xin Zhou(周昕)Rudolf Podgornik and Mingcheng Yang(楊明成)
1School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China
2Beijing National Laboratory for Condensed Matter Physics and Key Laboratory of Soft Matter Physics,Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China
3Songshan Lake Materials Laboratory,Dongguan 523808,China
4Wenzhou Institute,University of Chinese Academy of Sciences,Wenzhou 325001,China
Keywords: diffusion,composite channels,diffusio-osmotic flow,hydrodynamic effect
1. Introduction
Diffusive transport of molecules and colloidal particles in microscale channels is ubiquitous in physical, chemical,and biological processes,[1-12]and has been extensively studied. Prominent examples include transport of ions across membranes,[13-15]alkanes diffusion in zeolites,[16,17]water filtration through porous media,[18-20]and translocation of polynucleotides in living tissues.[21,22]Understanding the diffusion of small particles in microchannels is thus of fundamental importance for the development of microfluidics and nanotechnologies[23,24]as well as the design of advanced materials and smart devices.[25,26]
Previous related theoretical work mainly focused on the dynamics of small particles in corrugated microchannels with varying width but in the absence of hydrodynamic effects.[27-36]The non-flat channel wall introduces remarkable entropic effects,which critically influence the equilibrium and dynamic behavior of the diffusing particles. For the “dry”channels, a theoretical formulation, known as Fick-Jacobs(FJ) equation,[37]was proposed to describe the transport of Brownian particles in confined geometries,which can properly account for the entropic effects in particle diffusion. Nevertheless,recent experiments indicate that the hydrodynamic interactions between the particles and corrugated channel walls have a large impact also on the motion of the particles.[38,39]In more general confined environments,the hydrodynamic effects have also been shown to substantially affect the dynamics of suspending particles.[40-44]In the “wet” channels, the confinement wall is usually treated as either a no-slip or a slippassive boundary. However, in the context of active colloids,which have recently attracted considerable interest because of their non-equilibrium features and potential applications,driving boundary walls are prevalent.[45-48]The active colloidal particles often create a local gradient field(e.g.chemical,thermal or electric potential gradient) that can lead to a surface fluid flow along the nearby boundary wall due to the phoretic osmosis effect.[49-54]Such driving boundaries could be expected to be of paramount relevance to the colloidal diffusion in microchannels,although related investigation is rare.
In the present work,we perform mesoscale simulations to study the diffusive behaviors of a chemically active colloidal particle in a composite microchannel,constructed by alternating no-slip and diffusio-osmotic boundary walls. The chemical reaction catalyzed by the active colloidal particle creates a local chemical gradient along the channel wall, which drives a diffusio-osmotic flow parallel to the wall. We show that the surface flow can produce a strong hydrodynamic repulsion between the colloidal particle and diffusio-osmotic wall,and hence significantly change the configuration space accessible to the colloidal particle. By adjusting the surface properties of the channel wall, we can thus manipulate the position distribution of the colloidal particle and as a result, we are able to achieve different spatial patterns for the colloidal diffusion in a flat channel, seemingly similar to but essentially different from the case of the microchannels with corrugated geometries. Moreover, contrasting with the diffusion in geometrically corrugated channels, the diffusio-osmotic wall can largely enhance,instead of suppressing,the colloidal diffusivity.
2. Simulation method and systems
2.1. Solvent
To bridge the huge gap between the mesoscopic scales of the colloidal particle and the atomic scales of the solvent molecules, we employ a hybrid dynamics simulation scheme. The fluid is described by a particle-based mesoscopic method, known as multiparticle collision dynamics(MPC),[55-60]while the colloidial particle is modelled by standard molecular dynamics(MD).In MPC,the fluid is modelled by a collection of point-like particles with massm,continuous positionsri(t). The particle dynamics takes place by alternating streaming and collision steps. In the streaming step,the solvent particles move ballistically for a certain timeh.In the collision step, the particles are sorted into square cells of sizea, and interact only with particles in the same cell.Their velocities relative to the center-of-mass velocity of each cell are rotated by an angle around a randomly oriented axis,vi(t+δt)=vcm(t)+?(vi(t)-vcm(t)),wherevcmis the centerof mass velocity of the collision cell and ? is the rotational matrix. To guarantee the Galilean invariance,the grid of collision cells is randomly shifted before each collision step. This collision rule locally conserves mass,momentum,and energy,so that hydrodynamic interactions, mass diffusion and dissipation can be properly captured. Moreover, the thermal fluctuations are naturally involved in the MPC fluid. In order to consider a chemical gradient, the MPC solvent contains two types of particles,A and B.Both A-type and B-type particles take part in the MPC collision, irrespective of the identity of the particle species. Simulation units are reduced by settinga=1,m=1, and the system mean temperaturekBT=1(kBis the Boltzmann constant).Other MPC parameters used in the simulation areh=0.1 and the mean number of fluid particles per cellρ=10.
2.2. Colloidal particle
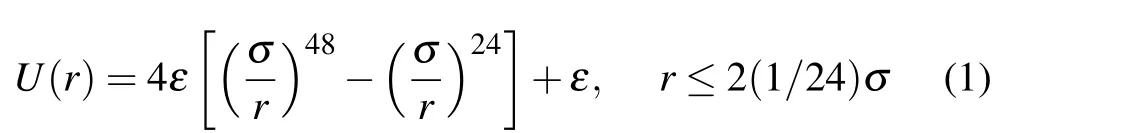
The colloidal particle is modeled by a single bead that interacts with the solvent particles via a repulsive Lennard-Jones(LJ)-type potential,with the potential intensityε=1 and the colloidal particle radiusσ=2.5. Here,ris the distance from the bead center. The chemically active colloidal particle can uniformly catalyze a chemical reaction of the solvent at its surface, so as to generate a chemical gradient around it. Specifically, the reaction A→B occurs upon a collision of A solvent particle with the colloidal particle, with an imposed probabilityPA. To conserve the concentration of the reactant A particle, an inverse reaction B→A is performed at the location far away from the colloidal particle,with a probabilityPB.In the simulations,the parametersPA=1 andPB=0.0001 are employed. Note that the catalytic colloidal particle is homogeneous and therefore lacks self-propulsion,experiencing only thermal motion in the bulk.
2.3. Composite channel
For simplicity,we consider a channel formed by two parallel walls in theydirection,with the periodic boundary conditions in thexandzdirections, as sketched in Fig. 1. The dimensions of the channel areLx×Ly×Lz=50×12×15.The planar walls have a composite surface and are constructed with alternating no-slip and diffusio-osmotic boundary conditions, which separately correspond to the black and red regions of Fig.1,having lengthsLnoslipandLosmotic,respectively.The two types of boundary conditions can be easily realized in the present mesoscale simulation. The no-slip boundary can be trivially realized by performing the bounce-back operation when the solvent particle is colliding with the wall,while the diffusio-osmotic boundary can be implemented by adding a selective driving operation to the no-slip boundary condition[61](Fig.1).
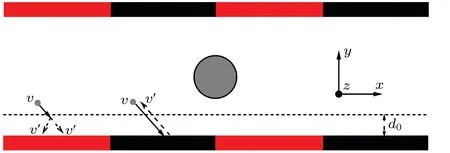
Fig. 1. Schematic diagram of the chemically active colloidal particle in a composite channel. Periodic boundary condition are performed in the x and z directions,and boundary walls are applied in the y direction. The boundary walls are composed of alternating no-slip and diffusio-osmotic boundary conditions, corresponding to the black and red regions of the wall, respectively. The grey sphere refers to the colloidal particle. Here,v and v'respectively refer to the fluid particle velocities before and after the bounce-back(black region) or driving operation (red region), and d0 to the prescribed interaction range of the driving operation.
Specifically,the driving operation reverses the tangential velocities of species B when they are located within a prescribed interaction ranged0, as sketched in Fig. 1. The driving operation can lead to a diffusio-osmotic flow along the gradient of B component parallel to the boundary wall. The magnitude of the osmotic flow increases with the interaction ranged0,and vanishes whend0=0(namely traditional no-slip wall). In the simulations, the driving operation is performed after each MPC step. In addition, the composite walls of the channel interact with the colloidal particle through the same repulsive LJ-type potential in Eq.(1).
3. Results and discussion
The system is initialized with all the solvent particles being species A. Due to the chemical reaction occurring at the surface of the chemically active colloidal particle, a stationary concentration gradient of species B is quickly established around the colloidal particle and decays with the distance from the colloidal particle. As the colloidal particle approaches the channel wall, the diffusio-osmotic surface can experience a noticeable tangential concentration gradient of B component and thus drive a diffusio-osmotic flow parallel to the wall along the tangential gradient of the reaction products (i.e., pointing toward the projection of the colloidal particle on the wall). To illustrate this, figure 2 depicts the flow field generated by a uniform diffusio-osmotic wall. Because of the mass continuity, the osmotic flow along the wall leads to a fluid flow into the bulk in the proximity of the catalytic colloidal particle,thus forming vortex structures. As a result, the colloidal sphere is pushed away from the wall, exhibiting an effective repulsion between the colloidal particle and wall. This effective interaction is of purely hydrodynamic origin and depends sensitively on the surface properties of the channel wall.
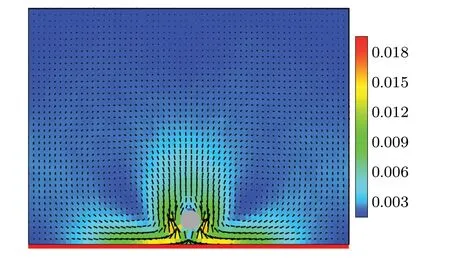
Fig.2.The xy cross-section of the flow field generated by a diffusio-osmotic wall under the local concentration gradient produced by the chemically catalytic colloidal particle,with d0=1.0.The color bars indicate the magnitude of the flow velocity.
Figure 3(b) shows the stationary probability distribution of the colloidal particle in a symmetric composite channel withd0=0.3.It is found there is a strong depletion area close to the diffusio-osmotic walls due to the repulsive particle-wall hydrodynamic interactions, limiting the configuration space accessible to the colloidal particle, while the colloidal particle is accumulated in the stick boundary region. Consequently,the particle probability distribution shows a corrugated structure,which is reminiscent of colloidal diffusion in corrugated channels with periodically varying width.[28,36,38,39,62]Nevertheless, in the present situation, the corrugated distribution exclusively arises from the hydrodynamic effects rather than the channel geometric (entropic) effects. Further, a stronger constraint is expected with the increases ofd0, as shown in Fig. 3(c), in which the colloidal particle is loosely trapped in the region of no-slip boundary. Contrarily,whend0=0(uniform no-slip wall) the colloidal probability distribution trivially becomes homogeneous,as shown in Fig.3(a).
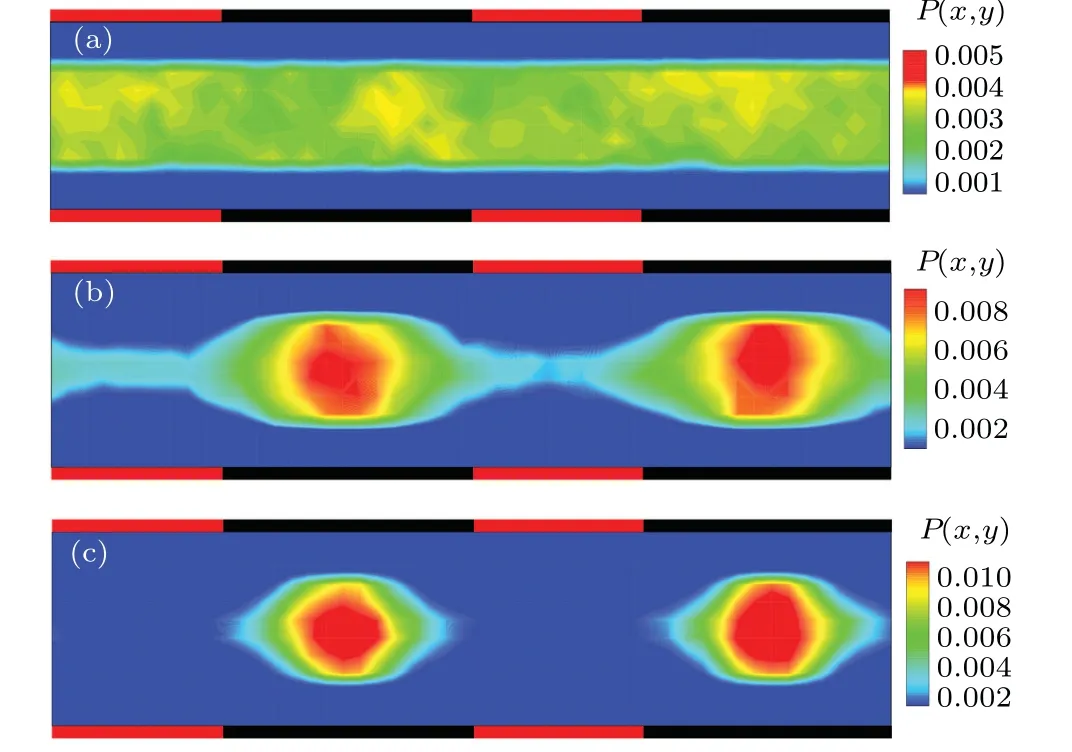
Fig.3. Probability distribution of the chemically active colloidal particle in the symmetric composite channel,with the interaction range of the driving operation (a) d0 =0, (b) d0 =0.3, and (c) d0 =1.0, respectively. The red and black walls separately correspond to the diffusio-osmotic(Losmotic=10)and no-slip(Lnoslip=15)boundaries.
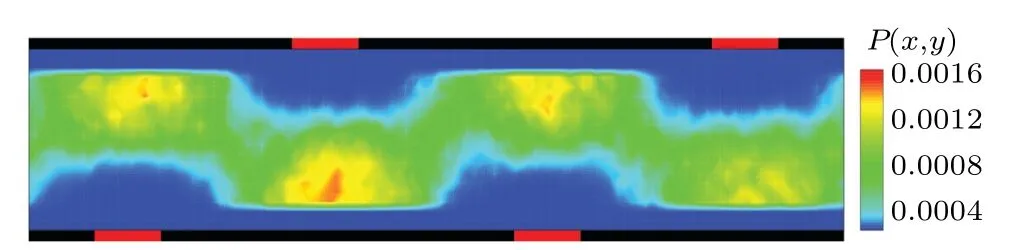
Fig. 4. Probability distribution of the colloidal particle in the nonsymmetric composite channel, in which the diffusio-osmotic and no-slip boundary units have a dimension of Losmotic=10 and Lnoslip=50,respectively. Here,d0=1.0 is used.
In the symmetric channel, the particle position distribution has a symmetric corrugated structure(Fig.3). By using a nonsymmetric composite channel, we can achieve a different pattern of the particle probability distribution. Figure 4 plots the probability distribution of the colloidal particle in an asymmetric composite channel. It is found that the space accessible for the colloidal particle forms a zigzag-like pipe. When the colloidal particle is subjected to an external force,it will drift along the virtual pipeline. More complex distribution patterns could be realized by modulating the structure of the flat channel walls and the intensity of the osmotic flow.
Next, we study the diffusion dynamics of the catalytic colloid by quantifying its local effective diffusivity,Dx,in thexdirection (along the channel). The diffusion coefficient is determined by the mean-squared displacement of the colloidal particle in thexdirection,〈Δ2x〉,for a time interval Δt=100.The value for Δtis chosen by making a compromise between the good statistics for the measurements and the localization ofDx. Figure 5 plots the quasi-local effective diffusion coefficientDxas a function of thexcoordinate of the colloidal particle in the symmetric channel. The diffusion coefficient changes non-monotonically with the position of the colloidal particle, showing a maximum near the diffusio-osmotic surface and a minimum in the no-slip region. Furthermore, the difference between the maximum and minimumDxincreases with the driving range of the diffusio-osmotic walld0, which trivially vanishes ford0=0. In other words,the colloidal diffusivity is highly enhanced in the confined region of the composite channel [see Figs. 3(b) and 3(c)], in stark contrast to the case of the corrugated channel with periodically varying channel width,[38]which has an opposite trend due to geometric confinement. So,the present colloidal diffusion dynamics in the composite channel cannot be treated by the FJ theory,which describes well the entropic effects in geometrically confined channels.
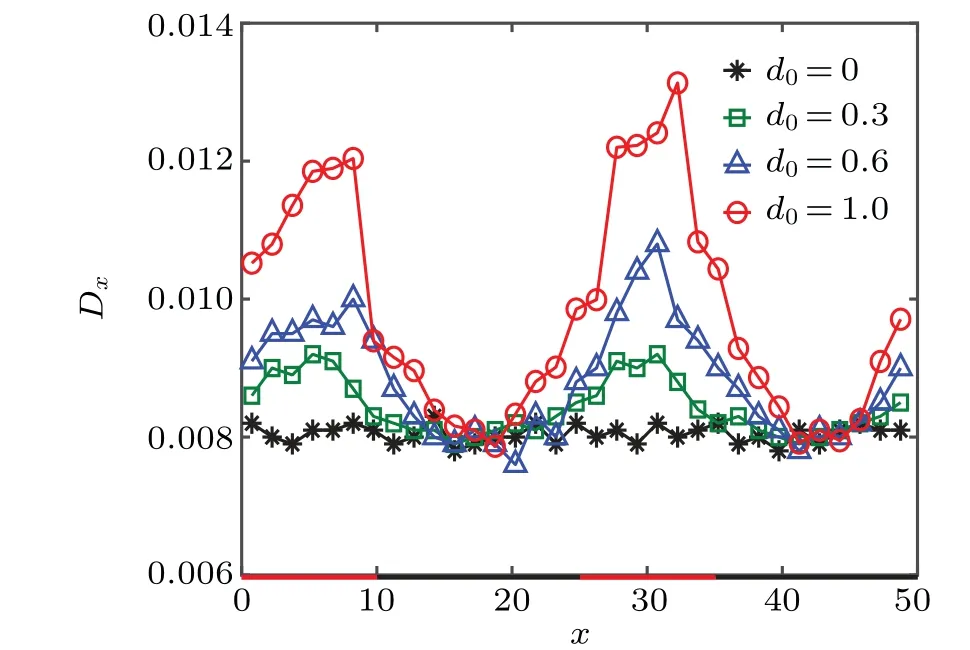
Fig.5. Local diffusion coefficient Dx of the catalytic colloidal particle in the symmetric composite channel for different d0.
The above counterintuitive results can be easily understood by analyzing the flow field generated by the diffusioosmotic wall. When the colloidal particle is located in the middle of the diffusio-osmotic region, the flow field is symmetric with respect to the particle,as shown in Fig.6(a).However,the“repulsive”diffusio-osmotic flow renders this region unstable for the catalytic colloidal particle and hence, once the colloidal particle enters the diffusio-osmotic region,it will leave quickly, resulting in an enhanced diffusivity. On the other hand, when the particle is located in the no-slip region far away from the diffusio-osmotic boundary, the flow field near the particle is very weak,as displayed in Fig.6(b),meaning that the colloidal particle is hardly affected by diffusioosmotic flow in this region and thus diffuses normally with a diffusion coefficient in the absence of the osmotic flow,as indicated by the result in Fig.5. In contrast,in the nonsymmetric composite channel (Fig. 4) the catalytic colloidal particle is not subjected to an effective hydrodynamic constraint and basically experiences a uniform environment along the channel. Thus,the colloidal diffusion coefficient in thexdirection is almost independent of thex-coordinate of the particle in this case(not shown).
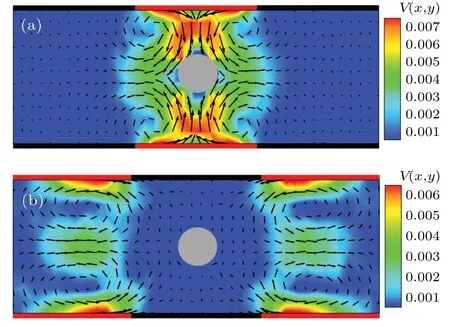
Fig. 6. Flow field in the symmetric composite channel generated by the diffusio-osmotic wall with d0 =1.0. In panels (a) and (b), the chemically active colloidal particle is located in the middle of the diffusio-osmotic and no-slip regions,respectively.
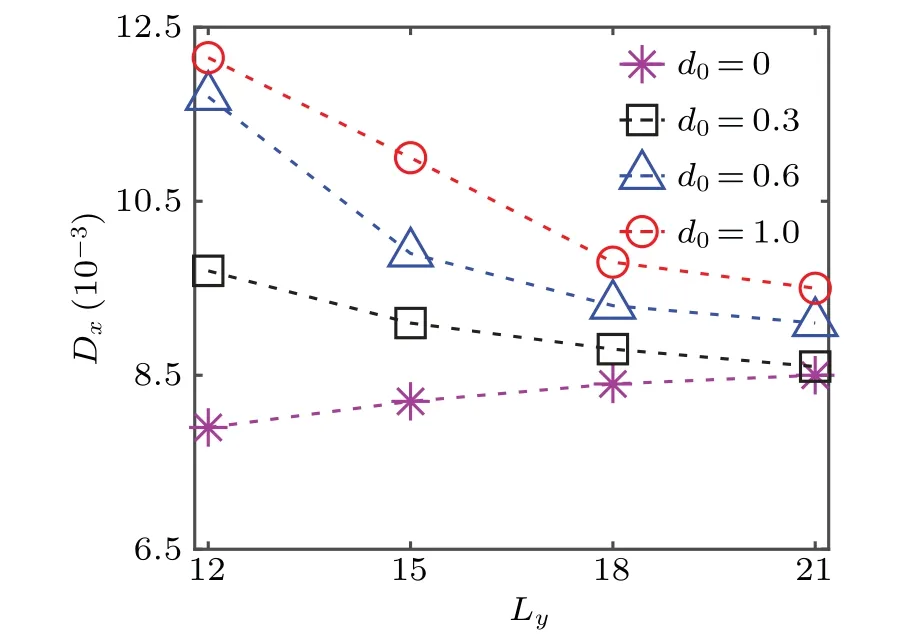
Fig.7. Local diffusion coefficient as a function of the width of the symmetric composite channel for different ranges of the driving operation d0.
Besides the surface properties, the channel widthLyhas also an important influence on the colloidal diffusivity. In Fig. 7, the diffusion coefficient of the catalytic particle located in the middle of the diffusio-osmotic region is plotted as a function ofLyfor different values ofd0. As the channel widens, the fluid flow driven by the diffusio-osmotic surface is reduced on the average. Consequently, the colloidalDxin the diffusio-osmotic region decreases with increasingLy, as shown in Fig. 7. While, ford0=0 (homogeneous noslip boundary),Dxis found to increase monotonically withLy,since the hydrodynamic interactions between the no-slip walls and particle, which suppress the particle diffusion,[38,39,63-65]weaken with the increase of the channel width. The diffusion coefficient of the catalytic colloidal particle locating in the noslip area has a similarLydependence as the case of the uniform no-slip channel,i.e.,d0=0(not shown).
4. Conclusion
We have performed hybrid dynamic simulations to study the diffusion behavior of a chemically active colloidal particle in a composite channel comprised of alternate no-slip and diffusio-osmotic walls.We show that the diffusio-osmotic surface can drive a marked flow field within the channel,as a response to the local chemical gradient induced by the catalytic colloid. The diffusio-osmotic flow can give rise to a hydrodynamic repulsion on the colloidal particle,and thus significantly changes its position distribution and diffusion dynamics. By varying the diffusio-osmotic flow intensity and the channel symmetry, we can achieve different patterns of the particle position distribution,including corrugated channel,loose trap and zigzag-like pipe patterns. Moreover,the diffusivity of the catalytic colloid is largely enhanced in the diffusio-osmotic area relative to the no-slip region. Our work thus proposes a promising strategy to manipulate colloidal particles in microchannels,and could be useful in microfluidic systems.
Acknowledgements
Project supported by the National Natural Science Foundation of China (Grant Nos. 11874397, 11674365, and 11774393)and the Strategic Priority Research Program of the Chinese Academy of Sciences(Grant No.XDB33000000).
- Chinese Physics B的其它文章
- Helium bubble formation and evolution in NiMo-Y2O3 alloy under He ion irradiation
- Dynamics and intermittent stochastic stabilization of a rumor spreading model with guidance mechanism in heterogeneous network
- Spectroscopy and scattering matrices with nitrogen atom:Rydberg states and optical oscillator strengths
- Low-overhead fault-tolerant error correction scheme based on quantum stabilizer codes
- Transmembrane transport of multicomponent liposome-nanoparticles into giant vesicles
- Molecular dynamics simulations of A-DNA in bivalent metal ions salt solution

