Effect of nonlinear translations on the pulsation of cavitation bubbles

Lingling Zhang(張玲玲), Weizhong Chen(陳偉中), Yang Shen(沈陽(yáng)), Yaorong Wu(武耀蓉),Guoying Zhao(趙幗英), and Shaoyang Kou(寇少楊)

Key Laboratory of Modern Acoustics(Ministry of Education),Institute of Acoustics,Nanjing University,Nanjing 210093,China

Keywords: bubble pulsation,bubble translation,nonlinear characteristics

1. Introduction

The tiny cavitation nuclei in liquid are activated by ultrasonic waves and grow into bubbles that are visible to the naked eye. This phenomenon is called acoustic cavitation and the bubbles are named cavitation bubbles.[1]The radial pulsation of the bubbles is based on the classical Rayleigh-Plesset equation[2]or the commonly used Keller-Miksis equation.[3]A cavitation bubble can be regard as a periodic pulsation in a periodic weak acoustic field. In fact, although the driving ultrasound can usually be periodic with time, the bubble pulsation is not always periodic[4,5]and can possess bifurcation.[6,7]Varga gave a classification of the bifurcation structure of a periodically driven gas bubble.[8]The pulsations of bubbles will possess stronger nonlinearity for a multiple-bubble system than for a single bubble.[9-16]Takahira found that the bifurcation structure of multiple bubbles with the same radii which were arrayed symmetrically in a sound field was similar to that of an isolated bubble driven by a sound of higher frequency.[14]Sugita investigated the bifurcation structures of coupled nonlinear oscillations of two spherical gas bubbles subject to a stationary sound field by means of nonlinear modal analysis.[15]Parlitz showed a sequence of bifurcation diagrams,exemplifying the recurrent pattern in the bifurcation set and its relation to the resonances of the system.[16]However,the translations of bubbles were not considered in these studies.

As is well known,the locations of bubbles do not remain unchanged in a liquid just because of the radiation force.[17]The translational motions of bubbles not only directly affect the distance between the centers of the two bubbles, but can also indirectly affect the pulsations of the bubbles. Therefore,it is reasonable to consider bubble translation.Equations of radial pulsations and translational motions of two coupled spherical cavitation bubbles were derived in Doinikov’s outstanding work.[18,19]On this theoretical basis the pulsations can be recalculated precisely. In this paper, the nonlinear characteristics of the pulsations are discussed when considering bubble translations.

2. The pulsations and translations of bubbles

Consider two spherical bubbles with radiiR1andR2located atx1andx2, respectively, on thex-axis in an incompressible fluid with liquid densityρ. The radiiR1andR2and locationsx1andx2, of course, obey their dynamic equations including two pulsation equations and two translation equations. The four dynamic equations are written as[18]

with

whereRi0is the ambient radius of thei-th bubble,ηis the viscosity of the liquid,ωis the angular frequency,p0is the hydrostatic pressure,γis the polytropic exponent of the gas within the bubbles,Dis the distance between the centers of the two bubbles,σis the surface tension andFηiis the drag force.[20]It is seen from Eqs. (1) and (2) that the pulsations and translations of bubbles influence each other, so it is reasonable to consider bubble translation. Equation (1) can be converted to the Keller-Miksis model for large forcing amplitudes,that is,the pulsation equations can be rewritten as[18]

withcbeing the speed of sound in the liquid.

3. The influence of nonlinear translations

Using Eqs. (2) and (5), the nonlinear characteristics of pulsations of bubbles are examined using the bifurcation diagram, one of the most important spectral analysis techniques in nonlinear dynamics. The MATLAB program package was used to calculate the dynamics characteristics of one of two bubbles,such as bubble 1. The driving frequency is set to the natural resonance frequencyf0using[21]

withpvbeing saturated vapor pressure of liquid. We set the physical parameters in our proposed model asp0=1.0 bar,ρ= 998 kg/m3,c= 1500 m/s,γ= 1.4,σ= 0.0725 N/m,R10=R20=6μm,andη=0.001 Pa·s.

3.1. The bifurcation behavior with pressure

The bifurcation diagram of the pulsation versus driving pressure for a movable bubble is plotted in Fig. 1(a). It is seen that the bubble pulsation appears as single period,multiperiod and even chaotic with the change of driving pressure.The bifurcation structure is divided into four regions. The bubble pulsation is period-one, period-doubling and periodmultiplying in regions I and III in Fig.1(a),but disordered in stages II and IV(see the shaded regions in Fig.1(a)).

For comparison,the bifurcation diagram of the pulsation versus driving pressure for an immovable bubble is plotted in Fig.1(b). It is seen that the bubble pulsation is disordered in region IV of Fig.1(a),but period-multiplying in region IV of Fig.1(b),which suggests that the nonlinear translation causes disorder of the pulsation. The nonlinear translation means that when the bubble moves in one dimension, the displacement per unit time is different. In addition, there is a slight difference in region III. The pulsation is period-multiplying in Fig. 1(a) but period-doubling in Fig. 1(b). Therefore, the phenomenon is caused by the translation. Finally, comparing Figs. 1(a) and 1(b) in region II, the bubble pulsation is also disordered,that is,even a single bubble pulsation still appears disordered. Thus,nonlinear pulsation itself can also cause the disorder of the bubble pulsation.

Fig.1. The bifurcation diagrams of pulsation versus driving pressure. Parts(a) and (b) show bubble pulsation for a movable bubble and an immovable bubble, respectively. The ambient radii are 6 μm, the driving frequency is 591 kHz and the initial distance is 800μm. The red points are the research objects in the following study.

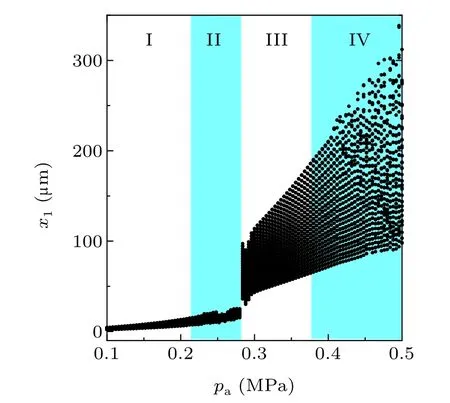
Fig. 2. The bifurcation diagram of translation versus driving pressure. The parameters are the same as those in Fig.1.

Figure 2 shows the bifurcation diagram of translation versus driving pressure. Of course, the bifurcation structure is also divided into four regions. The translation is period-one in region I and period-multiplying in regions II and III, but the location translation is mainly disordered in region IV. Thus,the disordered pulsation can be caused by the nonlinear translation in region IV, and the degree of disorder will increase with reduction of the distance between the centers of the two bubbles. To sum up,the nonlinear translation can disorder the pulsation in the case of certain parameters, and the degree of disorder of the pulsation can increase when two bubbles are close to each other.

3.2. Analysis of the phase diagram

In order to further understand the influence of the nonlinear translations on the pulsations,we select a driving pressure parameter in each region(see the red points in Fig.1(a)).Then,the bubble pulsations at different driving pressures are shown in Fig.3. It is seen that the bubble pulsation changes regularly in Figs.3(a)and 3(c)but irregularly in Figs.3(b)and 3(d)in the time domain.

Fig.3. The bubble pulsation. Parts(a), (b), (c)and(d)correspond to points o, p,q,and r of Fig.1(a),respectively.

Combined with other methods of judging disordered motion, the phase diagrams for a movable bubble are plotted in Fig. 4. The phase orbit is a closed curve inR-˙Rspace in Fig. 4(a), that is, the phase orbit passes through the Poincar′e section[22]from the same place every time, which means the pulsation is single period. In Fig. 4(c), the phase space orbit is closed by multiple cycles(see the inset),which means that the pulsation is period-multiplying. However,the phase point wanders randomly and never repeats its path in Figs.4(b)and 4(d), which confirms that the pulsation is disordered. Comparison with the phase diagrams for an immovable bubble(see Fig.5)shows that the pulsation is disordered in Fig.4(d)but period-quadrupling in Fig. 5(d). Thus, nonlinear translation can cause disordered pulsation. In addition, the pulsation is period-multiplying in Fig. 4(c) but period-doubling in Fig.5(c),which means that the nonlinear translation makes a large contribution to the pulsation.

Fig.4. The phase diagrams for a movable bubble. Parts(a), (b), (c)and(d)correspond to points o, p,q,and r of Fig.1(a),respectively. The inset to(c)corresponds to the red wireframe.

Fig.5. The phase diagrams for an immovable bubble. Parts(a),(b),(c)and(d)correspond to points s,t,u,and v of Fig.1(b),respectively. The insets in(c)and(d)correspond to the respective red wireframes.

3.3. Different ambient radii

The above discussion is about the effect of nonlinear translations on the pulsations when the ambient radii of two bubbles are the same. In this section, we mainly discuss the effect of nonlinear translations on the pulsations in the case of two bubbles with different ambient radii. Two sets of bubbles are selected for study.

It is seen from Figs.6 and 7 that the pulsation of the bubble with change in driving pressure still has similar characteristics to Fig. 1. Comparing the shaded regions in Fig. 6, the pulsation is disordered in Fig.6(a)but period-two in Fig.6(b).Similarly,the pulsation of the bubble in the shaded regions is very different in Fig. 7. The pulsation changes from periodtwo to disordered when considering bubble translation. This indicates that nonlinear translation can cause disorder of the pulsation for this set of parameters.In addition,when comparing the two groups of bubbles it can be seen that the ambient radius of bubble 2 also affects the pulsation of bubble 1.degree of disorder of the translation increases with reduction in the distance between the centers of the two bubbles.In addition,the phase diagrams also show that nonlinear translations make a large contribution to the pulsations,and can cause disordered pulsations.The same result can also be obtained when the two bubbles have different ambient radii,that is,nonlinear translations can cause disorder of the pulsations for certain parameters. To sum up, the pulsations of bubbles are greatly affected by translations of the bubbles.

Fig.6. The bifurcation diagrams of pulsation versus driving pressure. Parts(a)and(b)show bubble pulsations for a movable bubble and an immovable bubble, respectively. The ambient radii are 10 μm and 5 μm, respectively,the driving frequency is 343 kHz and the initial distance is 970μm.

Fig.7. The bifurcation diagrams of pulsation versus driving pressure. Parts(a) and (b) show bubble pulsation for a movable bubble and an immovable bubble,respectively. The ambient radii are 10μm and 5.5μm,respectively,the driving frequency is 343 kHz and the initial distance is 970μm.

4. Discussion and conclusion

The pulsations and translations of cavitati on bubbles obey combined ordinary differential equations,and their nonlinearities are studied in this paper using the bifurcation diagram and the phase diagram in a strong ultrasonic field. The bubble pulsation changes regularly or irregularly with changing driving pressure in the time domain. The bifurcation diagrams of the pulsation versus driving pressure show that there are nonlinear characteristics in the pulsations and translations of bubbles,and the disorder of the pulsations can be caused by the nonlinear translations of bubbles.In addition,the nonlinear pulsation itself can cause disorder of the pulsation. The bifurcation diagram of the translation is also examined, and shows that the

Acknowledgment

Project supported by the National Natural Science Foundation of China(Grant No.12074185).