Generation of elliptical isolated attosecond pulse from oriented H in a linearly polarized laser field

Yun-He Xing(邢云鶴), Jun Zhang(張軍), Xiao-Xin Huo(霍曉鑫), Qing-Yun Xu(徐清蕓), and Xue-Shen Liu(劉學深)

Institute of Atomic and Molecular Physics,Jilin University,Changchun 130012,China

Keywords: high harmonic generation,linearly polarized laser fields,elliptical isolated attosecond pulse,alignment angle,two-center interference effect

1. Introduction

High-order harmonic generation (HHG) with its equal frequency spacing and broad spectral coverage(from infrared to soft x-rays)has become a major tool for generating attosecond pulse[1-4]which can probe and track the ultrafast dynamical processes of the intra-molecular electrons,thus giving rise to extensive research.[5-8]The process of the HHG can be well explained by the semi-classical three-step model.[9]First, the electrons are ionized from the ground state under the action of a strong laser, then the electrons are accelerated in the laser field to gain energy, and finally the electrons are pulled back near the nucleus to emit energy when the laser field is reversed,which can generate the high-order harmonics.

Previous research works have been devoted to expanding the plateau of the harmonic spectrum[10]and improving the emission efficiency of the harmonic plateau,[11]which have made significant progress. In recent years, the elliptically polarized HHG has become a hot topic of research in theory[12-14]and experiment[15-17]because it has one more degree of freedom compared to the linearly polarized HHG and has more advantages in investigating the chiral,magnetic,and structural characteristics of materials. For example, the circular dichroism of photoelectrons is used to identify chiral molecules,[18]and the circular electron currents can be generated by circularly polarized attosecond pulses,which induce a strong magnetic field inside the molecule.[19]In addition, the measurements of harmonic spectra and ellipticity can also decode the multichannel dynamic processes in strong-field ionization of molecule.[20]

To obtain elliptically polarized harmonics,we can use an elliptically polarized laser field to act on atoms or molecules,but the efficiency of such elliptical harmonics decreases as the ellipticity of the driving laser increases.[21,22]In general,the atoms or molecules exposed to a linear polarization laser field can produce linearly polarized harmonics. The aligned molecules are used to generate elliptically polarized attosecond XUV radiation. For unaligned molecules, the emitted harmonics are polarized parallel to the polarization of the incident linearly polarized laser due to the symmetry. For aligned molecules, the laser-induced molecular alignment allows breaking the symmetry. A harmonic component perpendicular to the laser polarization is expected to be presented, leading to elliptical polarization of harmonic.[23,24]Zhouet al.[25]investigated the high harmonic from aligned N2molecule driven by a linearly polarized laser field. The degree of alignment〈cos2θ〉is estimated to be 0.65. The results show that the elliptically polarized harmonics from aligned molecules can be produced with ellipticity up to 0.35, which provides a method to obtain elliptically polarized HHG using the linear polarization laser field and attracts the exploration of the origin of such elliptically polarized harmonics. There are many reasons for this elliptical polarization, which can usually be attributed to the symmetry of the atomic molecular orbitals,[26-28]the interference between different excited-state emission channels[29]and the electron ionized at one atomic center within the molecule and recombined at another.[30]

In this work,we focus on the ellipticity of the harmonics from oriented H+2molecule exposed to a linear polarization laser field. The results show that the harmonic ellipticity depends strongly on the orientation angle. We can obtain a high ellipticity by adjusting the orientation angle and it can be generated atθ=30°,which is insensitive to the laser parameters.The position of the harmonic intensity minima indicates the high ellipticity, which can be explained by the two-center interference effect. The high ellipticity of the harmonics can be attributed to the phase difference of the harmonics in two directions(x,y). Finally,the elliptical isolated attosecond pulse with the ellipticity (ε=0.62) is synthesized by superposing the harmonic spectra of certain orders.

2. Theoretical method

whereRrepresents the intranuclear distance and its value is 2 a.u. andais the soft-core parameter set to 0.735, corresponding to the ionization energyIp=-29.6 eV,[31]which is close to the real ionization energy of the H+2molecule.θis the angle of the molecular axis with respect to thex-axis.VI(r)=r·E(t)=xEx(t)+yEy(t) represents the interaction potential energy between the molecule and the laser field.

We obtain the initial wave function by the method of imaginary evolution, and the electric field interacting with it is a linearly polarized laser field. Here, we assume that the polarization direction of the linearly polarized laser pulse is alone thex-axis. The molecular axis lies in thex-yplane and the angle with respect to thex-axis isθ. The laser pulse can be expressed as

andEy(t)=0,wheref(t)=exp[-2ln2(t/τ)2]is the Gaussian envelope,E0,ω0,τare the amplitude, frequency, pulse duration (full width at half maximum) of the driving laser pulse,respectively.

We solve the 2D TDSE by the method of the split operator.[32]The time and space steps are set to Δx=Δy=0.4 a.u and Δt=0.05 a.u., respectively. The spatial integration grid size is 409.6 a.u. In order to prevent the reflection of the wave function at the spatial boundary during calculation,we use an absorption function to eliminate the effect.[33]The HHG spectrum in thexandydirections can be obtained by the modulus squared of the Fourier transform of the timedependent dipole acceleration[34]〈¨r(t)〉,

whereη=|dy(ω)|/|dx(ω)|andδ=φy-φx.ηandδrepresent the amplitude ratio and phase difference in the two directions,respectively. To obtain the high ellipticity, the value ofηis close to 1, andδshould be near±π/2. If the intensities in the two directions are very different,or the phase difference is near 0 orπ,the ellipticity is small.[26,27,29,31]

3. Results and discussion

Figures 1(a1)-1(a4)show the ellipticity of the harmonics as a function of the harmonic orders and alignment angles with different wavelengths. The harmonic spectra are presented for those of high ellipticity. The intensity of the laser pulse isI=1.5×1014W/cm2and the FWHMτ=5 fs with 6 optical cycle. From Figs. 1(a1)-1(a4) we can find that the harmonic ellipticity is very small(near zero)around 0°and 90°, which is attributed to the symmetry of the molecule. Due to the polarization direction of the linearly polarized laser field along thexaxis and the cylindrical symmetry of the H+2molecule,the initial wave function at orientation angle 0°or 90°satisfiesφ0(x,y)=φ0(x,-y). The laser does not affect the symmetry of the wave function in theydirection and the wave function in theydirection hasψ(x,y,t)=ψ(x,-y,t). Therefore,

and there are no harmonics along theydirection at 0°or 90°.[24]The intensity ratio of harmonics in theyandxdirections is approximately zero. In addition, according to the SFA,[35]the harmonics of the two components are emitted at the same moment and the phase difference between them is zero. The conditions to obtain high ellipticity are not satisfied at 0°or 90°. So,we cannot observe the ellipticity of the HHG and the full harmonics emitted are linearly polarized.[36]

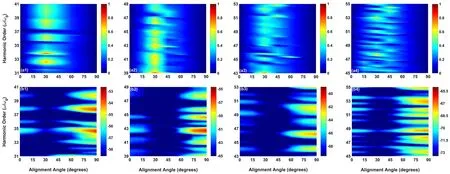
Fig.1. Harmonic ellipticity(a1)-(a4)and intensity(b1)-(b4)as a function of the orientation angle with wavelengths(a1),(b1)λ =800 nm;(a2),(b2)λ =900 nm;(a3),(b3)λ =1000 nm;(a4),(b4)λ =1100 nm. The intensity of the linearly polarized laser pulse is I=1.5×1014 W/cm2 with 6 optical cycles and the pulse duration τ =5 fs.

Figure 1(a1) shows the ellipticity of the harmonics as a function of the orientation angle withλ=800 nm.We can find that the ellipticity of the harmonics increases as the orientation angle increases from 0°to 30°, while it decreases from 30°to 90°. The ellipticity is relatively high between 15°and 45°compared to other orientation angles and the highest ellipticity(ε=0.83) is generated aroundθ=30°. Figure 1(a2) shows the ellipticity of the harmonics as a function of the orientation angle withλ=900 nm. We can see that the ellipticity of the harmonics increases as the orientation angle increases from 0°to 30°, while it decreases from 30°to 90°. The ellipticity is relatively high between 20°and 40°compared to other orientation angles and the highest ellipticity(ε=0.86)is generated aroundθ=30°.Figures 1(a3)and 1(a4)show the ellipticity of the harmonics withλ=1000 nm and 1100 nm, respectively.The high ellipticity is mainly distributed between 15°and 45°and the highest ellipticities are generated around 30°with a weaker ellipticity compared with the cases ofλ=800 nm and 900 nm. We can find that the orientation angle corresponding to the highest ellipticity is not sensitive to the wavelength and the highest ellipticity is always distributed aroundθ=30°.

To explain that the ellipticity has maxima atθ=30°,we present the harmonic intensity as a function of the molecule orientation angle,as shown in Figs.1(b1)-1(b4). We find that the harmonic intensity has minima aroundθ=30°as shown in Figs. 1(a1)-1(a4). The position of the harmonic intensity minima indicates the high ellipticity.[37,38]In general,the harmonic of parallel(x)laser polarization is dominant. However,at 30°, due to the two-center interference effect, the destructive interference inxdirection makes the harmonic intensities ofxandydirections comparable, meeting the first condition for large ellipticity. Second, for the harmonic minima, the phase of thexdirection changes by～πacross the minimum.Therefore,the phase difference of the two directions inevitably passes throughπ/2,meeting the second condition for large ellipticity.Therefore,the minimum of the harmonic corresponds to the maximum of the ellipticity.

The ellipticity of high-order harmonics generated by aligned molecules has been proposed in an orthogonal twocolor laser field. By adjusting the relative phase between the laser pulses, the elliptically polarized high-energy harmonics with high emission efficiency can be obtained.[39]Therefore,we might improve the intensity of the elliptical harmonic by changing the phase or appropriately increasing the laser intensity.

Figures 2(a)-2(d) show the ellipticity of the harmonics at alignment anglesθ=0°,30°,45°,60°with different wavelengths (a)λ=800 nm, (b)λ=900 nm, (c)λ=1000 nm,(d)λ=1100 nm.Overall view,the ellipticity of the harmonics is highest at 30°and lowest at 0°, while the ellipticity of 45°and 60°ranges between those of 0°and 30°,and the ellipticity of 45°is bigger than that of 60°. From Figs. 2(a)-2(d), one can see that the ellipticity of the harmonics withλ=900 nm is high and stable compared with the other cases. Therefore,we will take the case of wavelengthλ=900 nm as an example to explain the emission mechanism of the high ellipticity of the harmonics.

To further explain the potential physical mechanism of harmonic intensity that has a minimum atθ= 30°with a high ellipticity, we investigate the two-center interference of the molecule and analyze the phase difference of the harmonics between the two directions (x,y). For the two-center interference effect,we separately investigate the contribution of Coulomb potential from the two nuclei for the harmonics. The contribution of the Coulomb potential to the harmonic spectrum generated by each nucleus can be written as

From Fig.2(e),we can see that the difference of the harmonic intensities at alignment angleθ=0°including and ignoring interference effect is small. The constructive interference occurs around 41st, 43rd and 48th orders, while the destructive interference occurs around 40th,42nd,44th and 47th orders. From Fig. 2(f), it can be found that the harmonic intensities atθ=30°including interference effect are about 2 orders of magnitude weaker than that ignoring interference effect. From 39th to 49th orders, the destructive interference is very strong and dominant. From Fig. 2(g), the harmonic intensities atθ=45°including interference effect are about 1 orders of magnitude weaker than that ignoring interference effect. The destructive interference is also dominating from 39th to 49th orders. From Fig. 2(h), the harmonic intensities atθ= 60°including and ignoring the effect of interference are comparable. The destructive interference occurs mainly around 40th, 41st, 42nd, 44th and 47th orders, while the constructive interference occurs around 43rd and 46th orders. From Figs. 2(e)-2(h), the results show that the degree of the destructive interference is extremely strong atθ=30°,which results in the minimum of the harmonic intensity atθ=30°as shown in Fig.1(b2).

In Figs. 2(e)-2(h), we also show the phase difference(blue dotted line) of the two directions (x,y) of the harmonics at the orientation anglesθ=0°,30°,45°,60°. Figure 2(e)shows that there is a decreased trend(0.75πto 0)of the phase difference from 39th to 41st orders atθ=0°. From 41st to 49th harmonic orders the phase difference increases and then decreases between 0 and 0.25π. We can see that the phase difference is far away from 0.5πfrom the 39th to the 49th order. Figure 2(f)shows that the phase differences are all in the vicinity of 0.5πatθ=30°,which is consistent with the high ellipticity atθ=30°in Fig. 2(b). From Figs. 2(g)-2(h) the results show that the phase difference is also far away from 0.5π, so the ellipticity is smaller atθ=45°,60°than that atθ=30°as shown in Fig.2(b).

To investigate the influence of other laser parameters on the ellipticity of the harmonics,we present the ellipticity of the harmonics with different pulse durations and laser intensities as a function of the orientation angle. From Figs.3(a1)-3(a4)and 3(b1)-3(b4),we can see that the ellipticity of the harmonics is very small(near 0)atθ=0°and 90°,which means that the harmonics is linearly polarized and the results have been illustrated in Fig. 1. Figures 3(a1)-3(a4) show the ellipticity of the harmonics as a function of the different pulse durations 6 fs, 9 fs, 12 fs and 15 fs, respectively. The laser intensityI=1.5×1014W/cm2and wavelengthλ=900 nm are used.We can find that the ellipticity of the harmonics increases as the orientation angle increases from 0°to 90°, while it decreases from 30°to 90°. The ellipticity of the harmonics has maximum value(aroundε=0.6)at alignment angleθ=30°.

Figures 3(b1)-3(b4)show the ellipticity of the harmonics as a function of the orientation angle with different laser intensitiesI=2×1014W/cm2, 3×1014W/cm2, 4×1014W/cm2and 5×1014W/cm2, respectively. The wavelengthλ=900 nm and the pulse durationτ= 5 fs are used. From Figs.3(b1)-3(b4)we can see that the ellipticity of the harmonics increases as the alignment angle increases from 0°to 30°,while it decreases from 30°to 90°and the ellipticity of the harmonics also has maximum value(aroundε=0.5)at alignment angleθ=30°. Figures 3(a1)-3(a4)and 3(b1)-3(b4)show the common feature that the ellipticity of the harmonics has maximum value at alignment angleθ=30°, which is consistent with the results in Fig.1. Therefore,the high ellipticity is insensitive to the laser parameters but sensitive to the orientation angles.

Fig.2. Ellipticity of the HHG at the alignment angles θ =0°,30°,45°,60° with different wavelengths(a)λ =800 nm,(b)λ =900 nm,(c)λ =1000 nm,(d)λ =1100 nm. Harmonic spectrum obtained by including interference effects(red dashed line)and ignoring interference effects(black solid line) and the phase difference (blue dotted line) of the x and y directions of the harmonics with λ =900 nm generated at alignment angles(e)θ =0°,(f)θ =30°,(g)θ =45°,(h)θ =60°. The other laser parameters are the same as those in Fig.1.

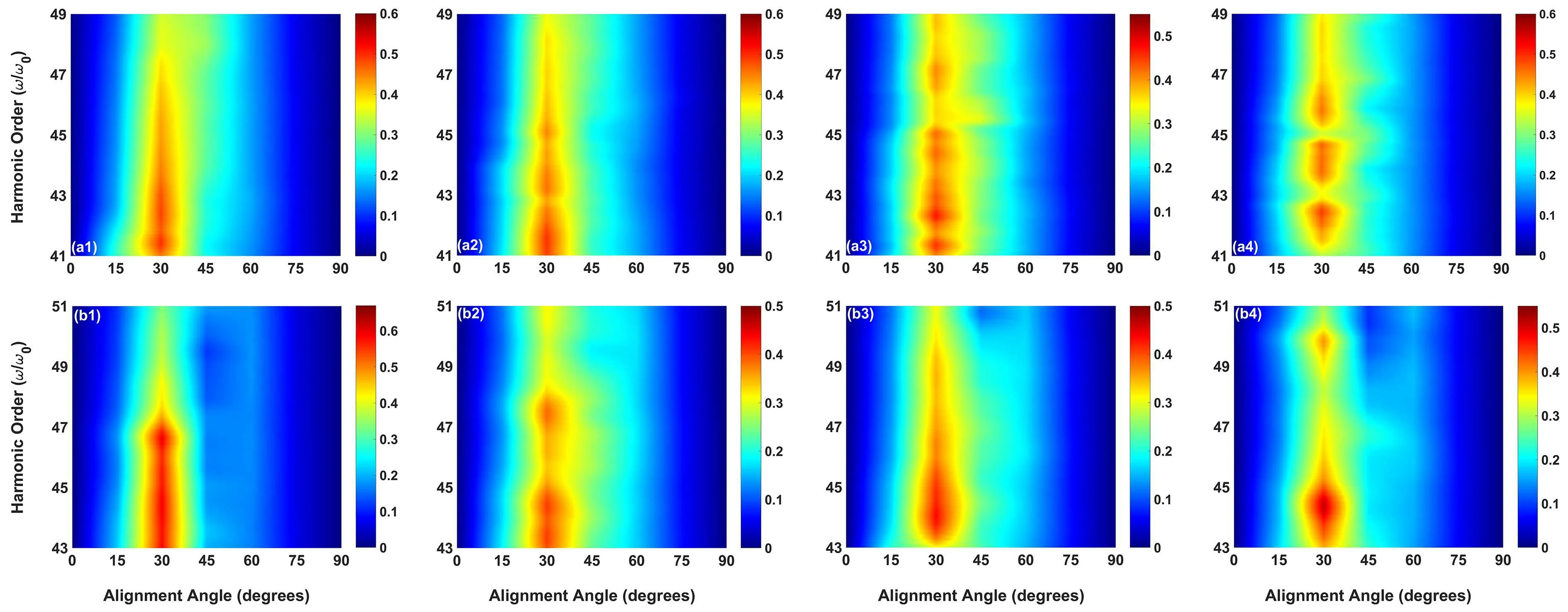
Fig.3. Ellipticity of the harmonics as a function of the orientation angle with different pulse durations(a1)6 fs,(a2)9 fs,(a3)12 fs,(a4)15 fs and laser intensities(b1)I=2×1014 W/cm2,(b2)I=3×1014 W/cm2,(b3)I=4×1014 W/cm2,(b4)I=5×1014 W/cm2.

Fig.4.(a)Temporal profile of the isolated attosecond pulse obtained by synthesizing harmonic orders from 17th to 47th. (b)Three-dimensional map of the isolated attosecond pulse generated by the electric field. The laser parameters are the same as those in Fig.1.

Figure 4(a) presents the synthesized attosecond pulse in the temporal domain. The attosecond pulse is synthesized from 17th to 47th harmonic orders for alignment angleθ=30°with the laser wavelengthλ=900 nm.We can see that the pulse duration of the isolated pulse is 65 as. Figure 4(b)shows the polarization characteristics of the attosecond pulse(yellow line). The red and green lines represent the projections of the attosecond electric field in thexandydirections,respectively.The blue line represents the projection of the electric field of the attosecond pulse on thex-yplane. In Fig. 4(b) it can be seen that the attosecond electric field is elliptically polarized with the ellipticity of 0.62.

4. Conclusion

In summary, we investigate the ellipticity of the HHG from the oriented H+2exposed to a linearly polarized laser field. The simulation results are obtained by numerically solving the 2D TDSE.Our results show that the high ellipticity can be generated at a particular angleθ=30°, which is strongly sensitive to the orientation angle of the molecule and not varied with the laser parameters such as wavelength,laser intensity,and pulse duration. The position with the high ellipticity corresponds to the harmonic intensity minima, which can be explained by the two-center interference effect. We demonstrate the origin of the high ellipticity generation by calculating the phase difference of the harmonics between thexandydirections. In addition,the ellipticity of the harmonics is very small at orientation angleθ=0°and 90°due to the symmetry of the molecule with respect to the laser. Finally, the elliptical isolated attosecond pulse withε=0.62 is synthesized by superposing the harmonic spectra of certain orders.

Acknowledgment

This work was supported by the National Natural Science Foundation of China(Grants Nos.12074142 and 11904122).