基于改進蜂群算法的醫療人力資源應急優化配置方法研究

姜鑫磊

（河北北方學院附屬第二醫院，河北張家口 075100）

在全球化的疫情背景下，無疫情地區的正常醫療服務保障對于維持我國社會穩定、保障突發性疫情擴散具有重要意義。我國醫療行業的競爭力從單一的醫療團隊素質、診斷水平與外部環境拓展為全方位的綜合能力，人力資源管理水平就是決定突發緊急情況下醫療行業平穩運營的重要因素。加強醫療人力資源的配置，對應對突發醫療負擔的考驗，具有重要意義。

為解決緊急突發情況下的醫療人力資源配置問題，文中引入了約束編程，一方面明確了問題所涉及的約束描述方法；另一方面，通過實驗分析，提出了解決問題的啟發式算法。

文中首先建立基于多目標約束的人力資源配置模型[1-2]，在分析了模型的局部與全局約束后，通過引入改進蜂群算法對該問題完成求解，并根據實驗情況調整部分算法的結構參數。

1 人力資源問題建模

為將先前描述的問題建模為約束滿足問題，將所有問題組件轉換為<變量，域，約束>形式。建模可以通過多種方式完成，文中提出一種基于變量的模型[3]，定義問題變量為個體i的時隙p，例如=sj表示將個體i分配給周期為p的服務是sj。定義該變量的主要原因是人力資源配置的解決方案必須是對所有個體在整個時期內的完整分配[4-5]。

1.1 完整性約束

對于人力資源集合中的任意個體，需滿足[6]：

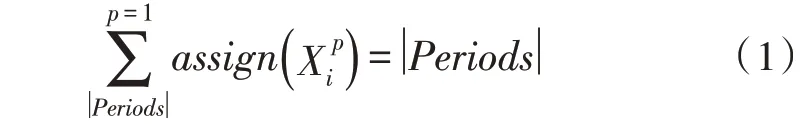
設域D={s1,s2,…,sn}，人力資源分配單元（UH）中，n個分配單元集合是所有約束滿足問題變量的域。=sj表示個體i在服務周期sj內受時間階段p的影響[7]。

1.2 約束條件

如上節所述，該問題有兩種類型的約束：第一種類型表示與個體相關的約束，用于確定個體與自身周期的關系；第二種描述個體與其所處服務之間的關系。

為合理表達上述約束，文中考慮人力資源合集的強制性服務列表中為所有個體提供的固定義務服務數量m(m∈[1,|OS|])，對于任意的人力資源個體，應滿足下述公式[8]：

此外，該模型仍需滿足基本約束：每個個體在給定的時間段p中均擁有基本服務si，以及在下一個時期分配個體p+1 到服務si。對于任意一個基礎的服務FS=，任意的時間間隙p∈[1,∣Periods∣]與任意的人力資源個體需滿足下述公式：

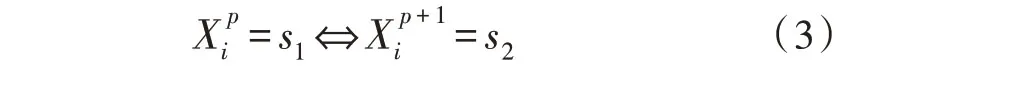
對于任意個體在資源分配的最后階段，限制條件應滿足下述公式：

在全局約束中，由于規劃容量限制，所以每個服務容量均不能超過約束條件。即對于任意s∈services以及任意p∈[1,∣Periods∣]，應滿足下述約束：

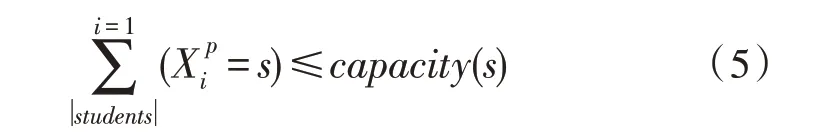
1.3 優化目標建模

服務占用率對于解決方案的質量具有重要的意義。因此對于每項服務i，定義Oi為占用率，Ci為其容量，Ei為超出值：

上式需滿足Ei≤0，即要維持i的容量；否則，服務將過載。后續的操作旨在確保盡可能維持或最小程度地破壞服務容量。因此對于任意服務i，任意周期內p，全局約束將由目標函數Minimize()代替。

2 基于改進蜂群算法的優化方法

為解決提出的人力資源優化問題，引入了蜂群算法。在標準蜂群算法中，所用蜜蜂的數量等于旁觀者蜜蜂數量，即其數量等于蜜蜂總數的一半[9]。為了模擬自然界中的蜜蜂運動方式，改進蜂群算法中定義了不同的參數，包括蜜蜂編號（BN）、食物來源編號（SN）、重復次數（MCN）、為產生新答案而變化的變量數量（Ndim）以及失敗數量上限[10]。

在人工蜂群算法中，若新的目標函數值改變，則需要重新設計解決方案，并用新的解決方案替換舊的解決方案[11]。但若新的目標函數值未顯示任何改善，則主要解決方案仍存在。為改善這樣的問題，提出了基于標準蜂群算法的改進方法。通過將旁觀者蜜蜂的數量設置為蜜蜂總數的不同百分比，并選取最佳百分比[12]，因此蜂群方程輔助解變為：

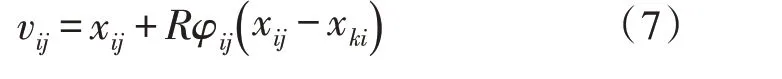
其中，R為鄰域半徑，其他參數已預先定義。提出了以下方程式以確定鄰域半徑[13]：

其中，cycle為迭代次數，MCN為迭代總數，A和G為預先設定的常數。

與標準蜂群算法相比，改進蜂群算法（IABC）的特殊優勢如下[14]：其可以更優地進行蜂群偵察蜜源與獲取蜜源之間的交互。應該注意的是，蜂群偵察是算法廣泛探索問題的空間搜索能力，獲取蜜源是算法探索局部解決方案鄰域附近的能力。為了在蜂群偵察蜜源與獲取蜜源間尋找平衡，通過對兩種改進蜂群算法進行對比，選取符合實際應用標準的改進算法[15]。

在此，提出了兩種后綴為1和2的部分約束改良人工蜂群（PCIABC）算法，將其分別稱為PCIABC1、PCIABC2。通過分析論證，設計實驗考察兩種改進方法[16]。

在PCIABC1 改進算法中，人力資源庫的每個尺寸參數表示在每個操作時間段分配的人力資源。在運行時間段，人力資源總數保持不變，使用連續性方程和人力資源總數約束條件來計算人力資源的高維新邊界，代表每個運行時間段的人力資源儲備，因此可以獲得以下方程式：

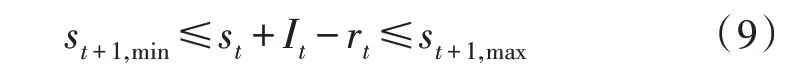
根據上式可推導出用于選取在每個運行時間段t內人力資源的分配方法：

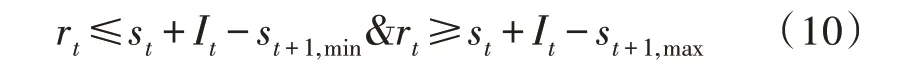
將此新界限與原始人力資源分配約束相結合，產生新的人力資源分配約束如下所示：

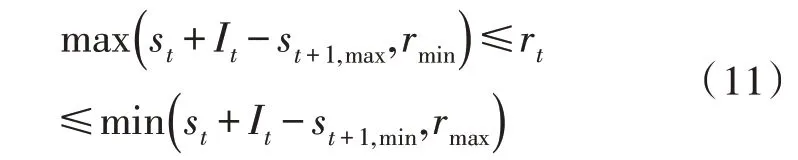
由實驗可知，使用上式得到的解是可行的。在改進算法的第二種形式PCIABC2 中，解決方案的每個維度代表每個操作時間段結束時剩余的人力資源。假設在操作時間段開始時已知人力資源數目，則使用連續性方程計算人力資源的高維邊界，以表示每個操作時間段結束時人力資源的剩余情況和限制分配約束。使用連續性方程來計算在時間段t內的人力資源分配量，并將該值替換為分配約束條件，可獲得以下不等式：

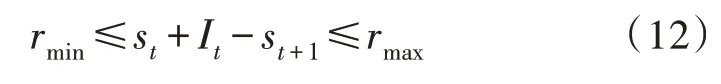
對于每個分配時間段t結束時人力資源的剩余量，綜合考慮新界限與原始人力資源約束條件，將產生新的人力資源釋放約束條件，如下所示：

經數值實驗測試可知，上式得出的解是可行的。

3 實驗驗證

下面結合實驗針對實際情況以調整算法的實際運行邏輯，從而得出最佳解決方案。

在突發緊急情況下，數據可視化在人力資源分配過程中扮演著重要的角色，對于掌控實時人力資源配置結果，輔助調度決策具有重要意義。目前常用的通用可視化工具是GIS，它可以在各類地圖中以多種可視方式顯示數據。但僅依靠GIS 可視化軟件難以獲得更多的免費數據計算和分析，因此在編寫人力資源可視化與調配軟件時，使用C＃編程中嵌入的ArcGIS Engine 構建一個特殊的GIS 應用程序，以實現數據的空間可視化。該界面實現了多種自由控制模式，支持調整顯示時間范圍、區域范圍和人力類型范圍并執行區域統計。

可視化軟件后端基于Fc-means 聚類算法和簡單線性迭代聚類（SLIC）算法優化了數據的計算與聚類，以便該聚類算法可以平衡數據的空間位置和人力資源流動。優化聚類的網絡結構如圖1 所示。

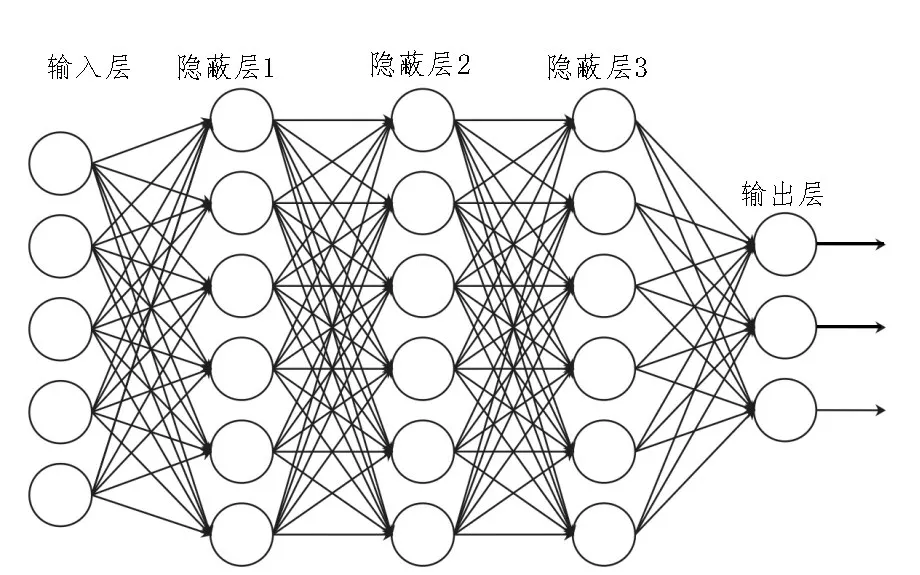
圖1 優化結構圖

為了改進先前專注于服務端的優化模型，通過提出一種針對人力資源的改進模型來處理涉及人力端的另一個優化模型。提出了基于Pareto front citepareto 方法的多目標優化模型，該模型可以通過改進之前的模型處理人力資源分配策略。

為改進多目標優化算法，添加了另一個客觀約束，代表人力資源分配的偏好。因此，目標函數改為：

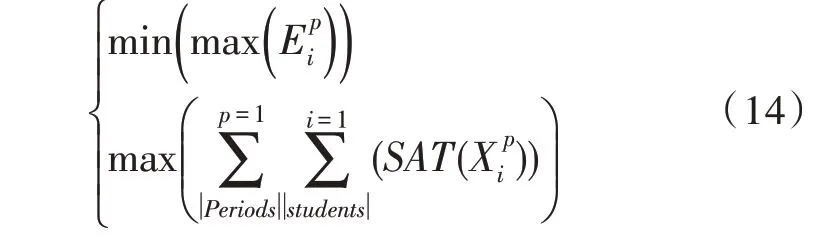
在統計實驗中，人力資源管理者在6 個調度周期中選擇兩個不同的周期，并使用優化場景對先前的配置進行實驗。圖2 與圖3 分別為單目標優化模型和多目標優化模型實驗的結果。

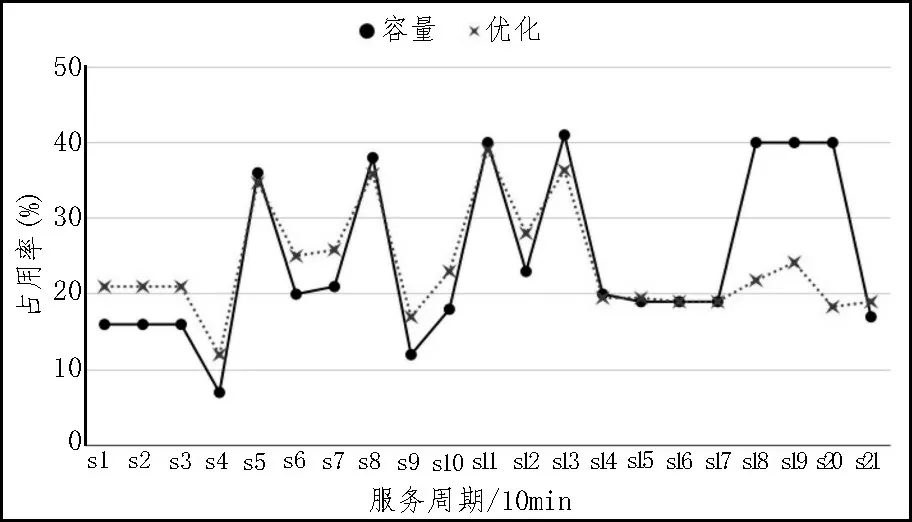
圖2 單目標優化實驗結果

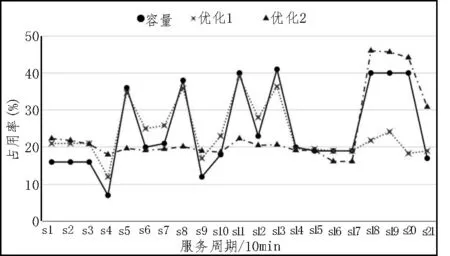
圖3 多目標優化實驗結果

通過分析可知，所選擇的偏好模型滿足了59%的人力資源管理者（10%的人力資源管理者完全滿意，49%的人力資源管理者部分滿意）。由于所設計方法中對目標設置進行了優化處理，所以多目標滿意度實驗結果也體現出了該算法可以同時優化服務和管理者的滿意度。

表1 為對設計的多目標模型進行2 000 萬次調度執行，通過硬約束或設置上限閾值等方法，將最大超過容量限制在27%以下的迭代計算實驗結果。

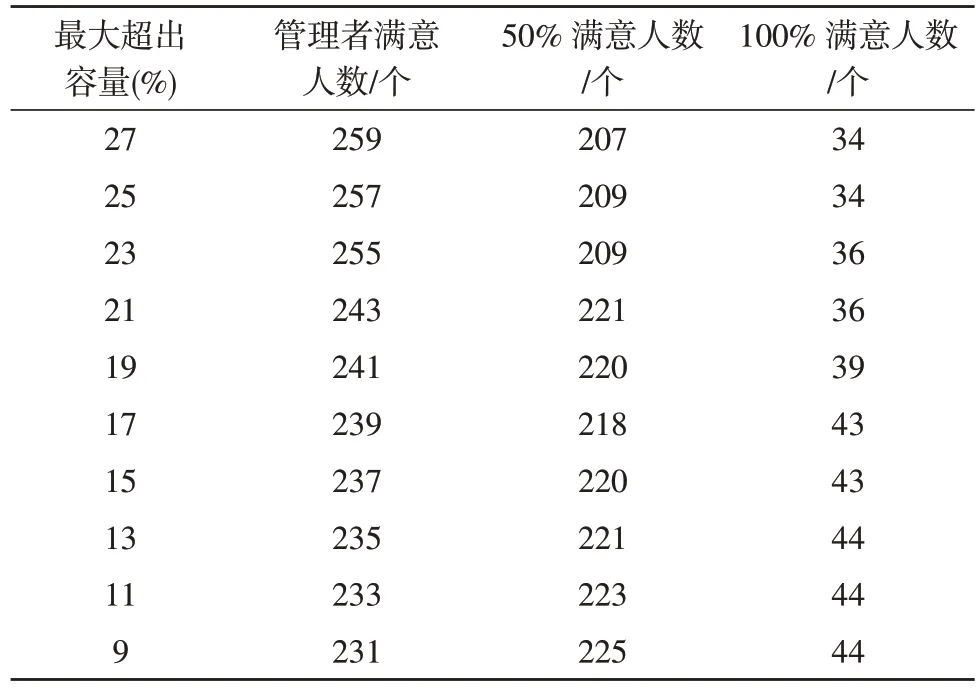
表1 管理者滿意度與容量溢出對比實驗

圖4 為將極限時間固定為20 min 時，所有可能解決方案中最大服務溢出能力與管理者滿意人數的關系，體現出了該模型的Pareto 邊界。從圖中可以看出兩個目標函數是相關的，因此需要對多目標同步優化，這對所提方法的具體應用具有重要的指導意義。

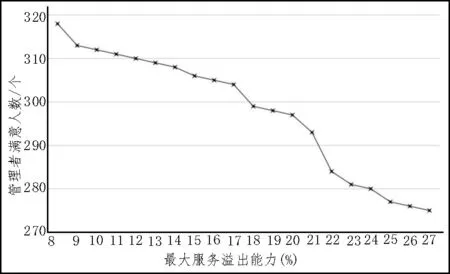
圖4 最大服務溢出能力

4 結束語

文中研究了在突發緊急公共衛生危機的情況下，醫療系統分配人力資源的實際方法。通過將此問題建模為多目標優化問題，并使用蜂群算法進行建模，完成智能化的人力資源優化配置。實驗結果證明，通過將突發緊急情況的服務需求轉換為多目標優化問題的軟約束，能夠達到良好的服務溢出效果，以實現無疫情區域的醫療人力資源的合理調度。