一種低時延低資源消耗的高精度鑒相方法

電子信息控制重點實驗室 孫洪波

干涉儀測向具有測向精度高、算法簡單、設備量適中的優點，高精度的相位測量直接決定了干涉儀的測向精度，文章介紹了一種優化的頻域鑒相方法，能有效的減小資源消耗與時間消耗，實現了實時大帶寬數據吞吐，取得了很好的效果。

干涉儀測向是一種高精度的測向體制， 廣泛應用在單站無源測向定位系統中，是電子偵察的一項重要技術。隨著工藝水平的提高，系統的集成度越來越高，適中的規模、高精度的性能使得干涉儀應用越來越廣泛。

通過通道間相位差的測量計算目標來波的到達方向，相位差測量的精度決定著測向的精度，高精度的相位測量方法消耗較多的處理資源，同時也需要較大的處理延遲，本文針對這兩點進行了相關研究，介紹了一種低時延低資源消耗的高精度鑒相方法。

1 高精度相位測量分析

如圖1所示為目前數字干涉儀測向處理的模型框圖，從圖中可以看出，某一遠距離對象輻射的電磁信號通過空間傳輸，進入接收設備的天線，通過射頻通道的低噪放大，變頻等處理，射頻信號轉換成可AD采集的中頻信號，在中頻上完成AD采集與后續數字處理，最終在數字上完成通道間相位差測量。

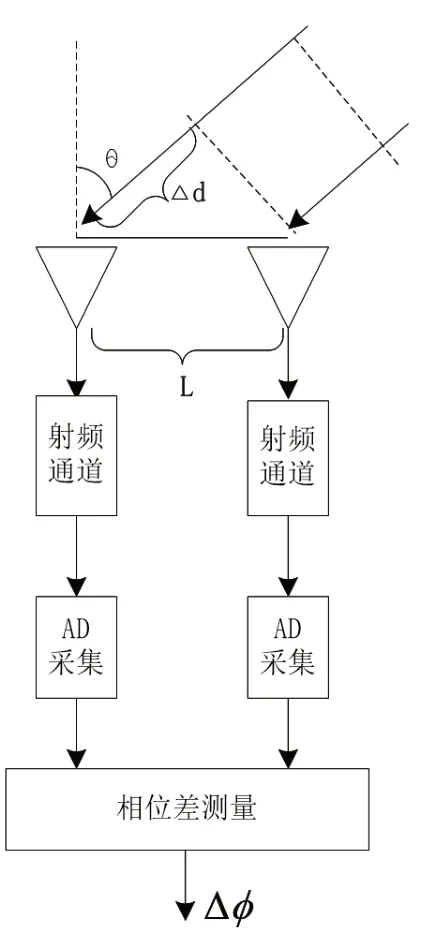
圖1 干涉儀原理模型Fig.1 Interferometer model

圖中可以看出，輻射電磁波信號到達接收設備的不同天線時，會存在一個路程差△d，該路程差使得同一個信號到達兩個天線的初相不同，最終體現為兩個通道的測量相位差，依據這個測量得到理想相差△φ，按照天線間距、波長的相互關系折算，可實現對該信號相對于接收設備到達方向角θ的測量（即完成測向）。

干涉儀測向的數學公式為：

其中Δφ入為由波程差造成的在兩個天線輸入的來波相位差，即測量的理想相位差，c為光速，f為信號頻率，L為兩個天線之間的間距。

對于雷達脈沖而言，信號形式主要表現為常規單載頻脈沖、線性調頻脈沖、相位編碼脈沖，對于常規單載頻信號，兩個通道的信號可描述為

瞬時相位差Δφ12(t)=ω0*t0，因此在脈沖觀察期間，可進行統計平均，取得較好的測量精度

對于線性調頻信號，兩個通道的信號可描述為

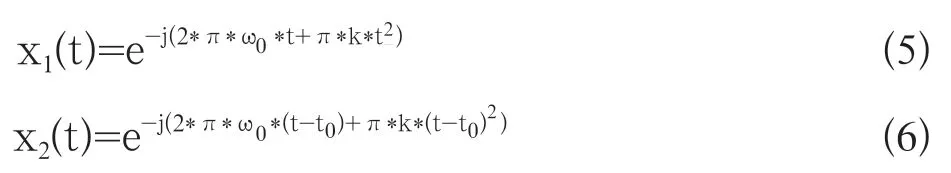
兩個通道的瞬時相位差有

以3m的基線為例，在[-60，+60]空域范圍內兩個通道間的延遲t0小于10ns，因此π*k*t02可忽略。

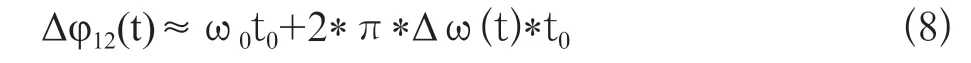
取ω0為脈沖的中心頻率時，t∈[-pw/2，pw/2]。

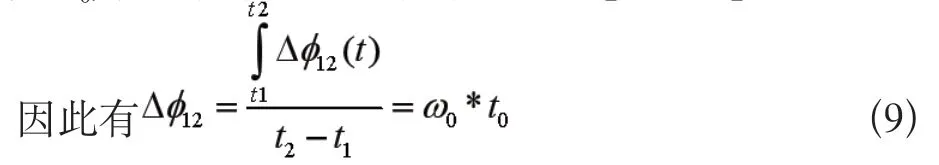
從上式可以看出統計后信號中心頻點處的相位差描述了通道間的相位差。

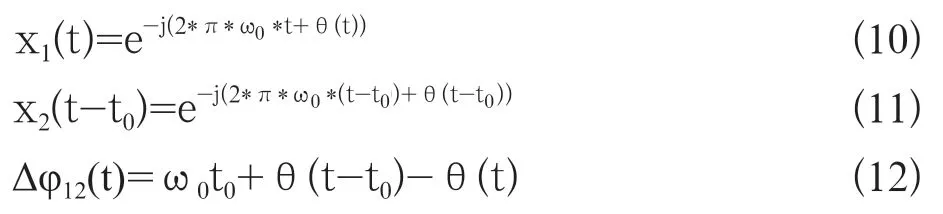
通常情況下延遲t0遠小于碼元寬度，因此在碼元內處理延遲t0部分外，θ(t-t0)-θ(t)=0，因此扣除相位跳變點后的統計平均有

因此有載頻的相位差描述了通道間的相位差。

綜上所述，對于常見的雷達脈內調制樣式，信號中心頻率點的相位差體現了波程導致的通道相位差，因此可通過提取中心頻點的相位差分求解信號的相位差，從而完成高精度干涉儀測向[1-2]。

2 高效測量方法設計

2.1 低資源DFT測相方法

從前面的分析可知，信號中心頻點的相位差反應了目標方向角信息，測量出中心頻點的相位差便可解算出目標角度，相位差的測量精度直接決定了目標角度的測量精度。

為了測量出信號中心頻點的相位，傳統的處理框圖如圖2所示。

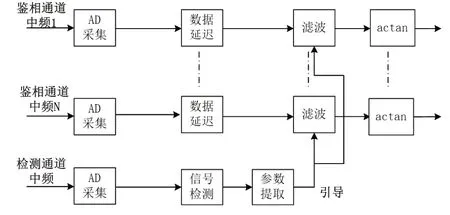
圖2 傳統測相框圖Fig.2 Traditional phase measuring block diagram

為了實現高增益處理接收，需要對噪聲進行抑制，提高處理信噪比，框圖中濾波框的目的就是提高信號信噪比，從而提高干涉儀鑒相精度。

對濾波后目標信號采用actan函數進行相位測量時，相位測量精度有[3]

對于大帶寬高采樣率而言，傳統做法中窄帶濾波需要濾波器階數很高，數字處理的資源消耗大。

FFT是一種等效的濾波器，較時域濾波器方法能較大的節省處理資源[4-5]。

按照FFT的公式有

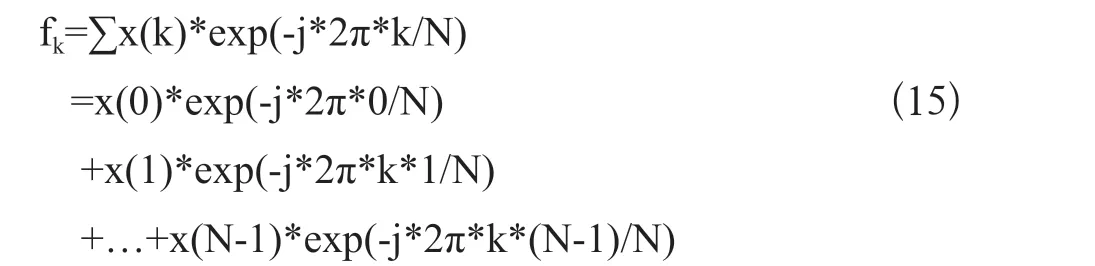
考慮到

上式可等效為

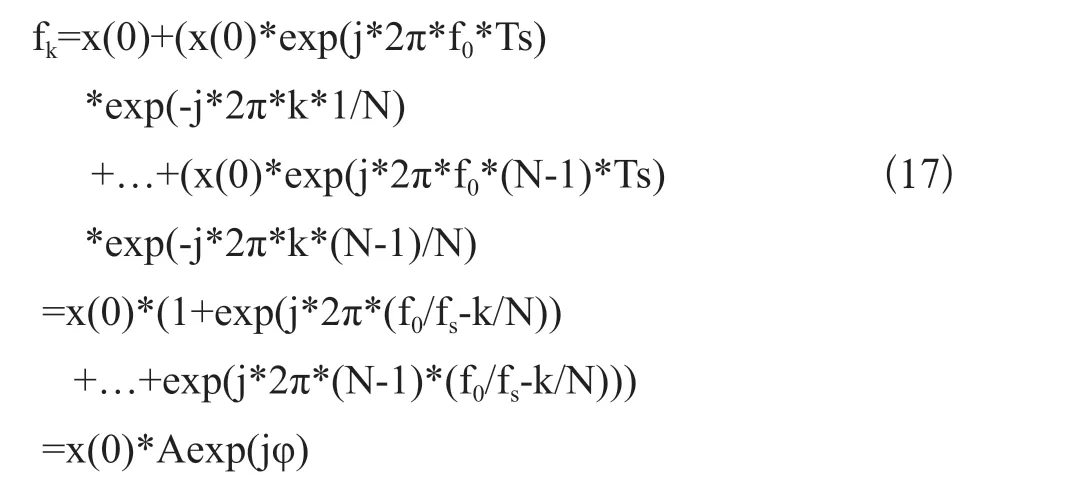
從上式可以看出fk體現了當前幀輸入數據的初相關系，為了提取各通道的相位差信息，可通過fk得到數據的相對初相值，最終得到干涉儀各基線的相位差。

FFT運算過程除了得到信號所在頻點的fk值外，還得到了其他無用頻點值，為了節省資源，可基于檢測結果，不再計算其他無效頻點值，僅計算信號頻點，資源因此將會得到較大的節省。

DFT測相方法正是基于這個思路進行設計的，僅計算fk頻點值，從FFT的原理可知，第K個頻譜點的

旋轉因子有如下關系。

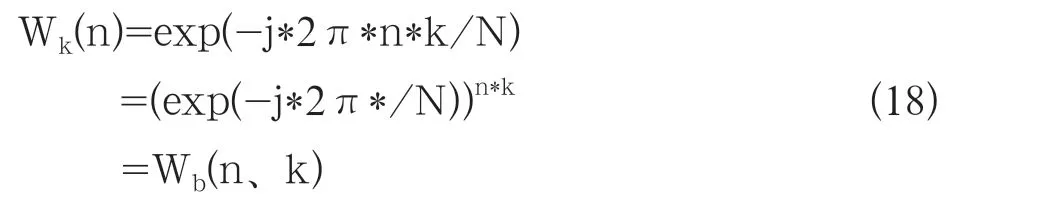
旋轉因子Wk(n)可通過基礎因子Wb(n)得到，工程中可將基礎因子Wb(n)做成查找表，頻率點K折算成相應的地址步進，可快速獲取第K點的旋轉因子。

依據上述的分析，DFT測相方法實現框圖如圖3所示。

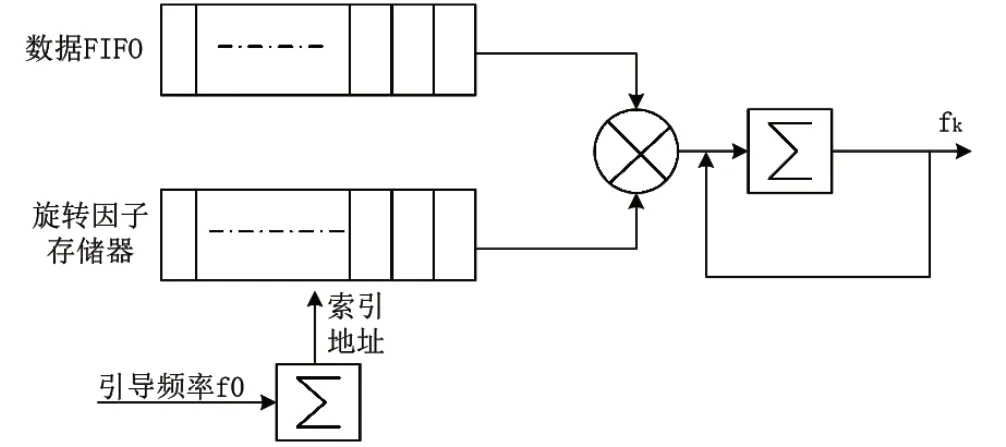
圖3 DFT測相框圖Fig.3 DFT phase measuring diagram

從圖中可以看出，DFT測相方法的實現采用了簡單的復數乘加運算實現，非常方便FPGA類硬件邏輯實現。數據采用FIFO緩存，實現采樣數據率與不同處理時鐘的銜接，而旋轉因子預先存儲在存儲器中，依據檢測引導頻率實現地址計算，引導頻率決定了累加的步進，依據索引地址讀取fk對應的旋轉因子，每個周期產生一次乘累加，N個時鐘周期后便可獲得fk的值。

2.2 DFT優化測相方法

進一步對測相方法進行優化。

旋轉因子有如下特性

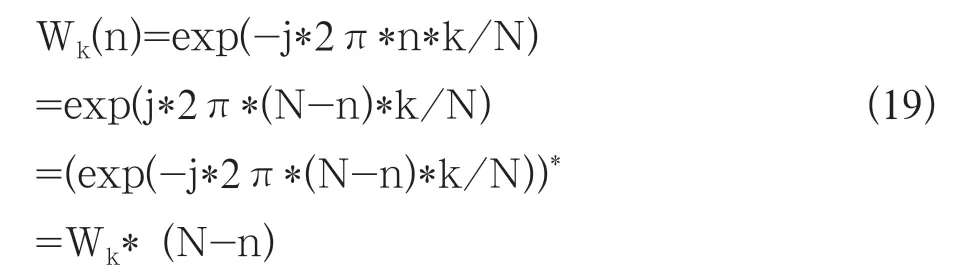
從上式可以看出，第一個采樣點與最后一個采樣點對應的旋轉因子互為共軛關系。

對于實采樣系統，系統可進一步優化，利用第n點與N-n的共軛特性，第n采樣點與N-n采樣點同時

運算，整個處理時間將會降為N/2。

優化后的實現框圖如圖4所示。

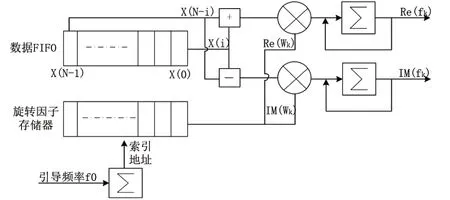
圖4 高效測相框圖Fig.4 Efficient method diagram

上述DFT或FFT方法實現鑒相處理，利用了FFT的等效濾波原理，但這種濾波器的旁瓣抑制卻僅為13dB。在同時多信號的情況下，弱信號會遭受強信號的干擾影響，影響的程度與兩個信號的頻率間隔、功率差以及初相相關，旁瓣影響的表現形式為信號測量相位差均值出現漂移，如表1所示。

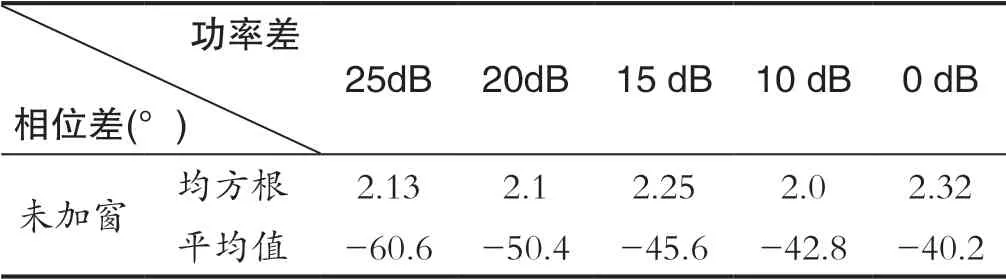
表1 多信號相位影響表Tab.1 Effect of multi signal

下表中兩個通道的理論相位差為40°，兩個信號的頻率差40MHz，隨著功率差的變化，原始DFT方法的相位差發生偏移，而25dB的功率差下，相位差漂移了近20°。

為了抑制高旁瓣的影響，采用特殊窗函數，降低同時多信號間旁瓣干擾，常用的窗函數有hamming、hanning等，經過加窗處理后相位測量的雙音性能將得到較大的提升。

加窗優化后的處理框圖如圖5所示。

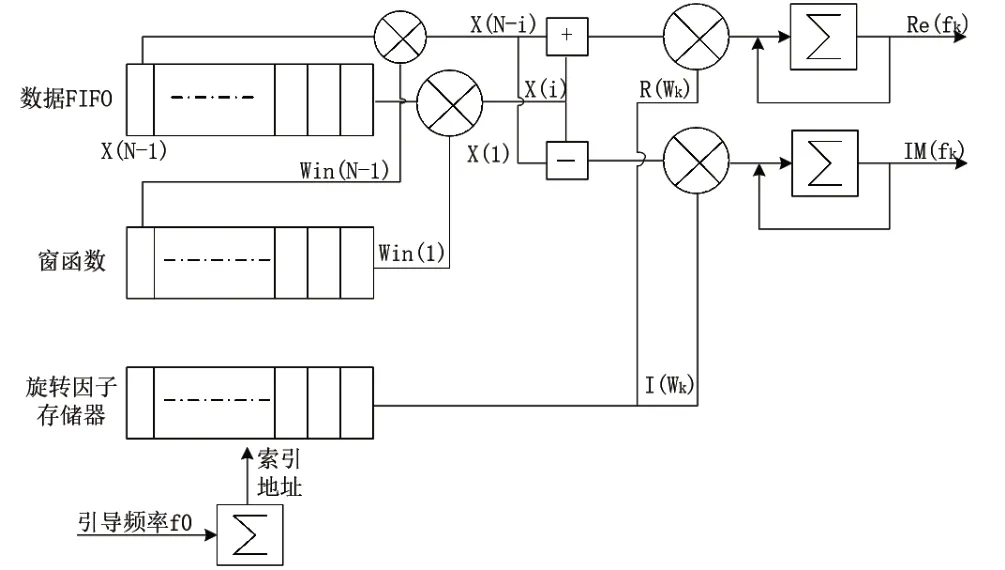
圖5 優化的DFT測相框圖Fig.5 Optimum diagram based on DFT method

加窗后的DFT相位測量方法相位測量結果如表2所示，從表中數據可以看出，加窗后隨著兩個信號的功率差增大，相位中心與相位誤差均沒有發生改變，體現了真實的輸入相位差。

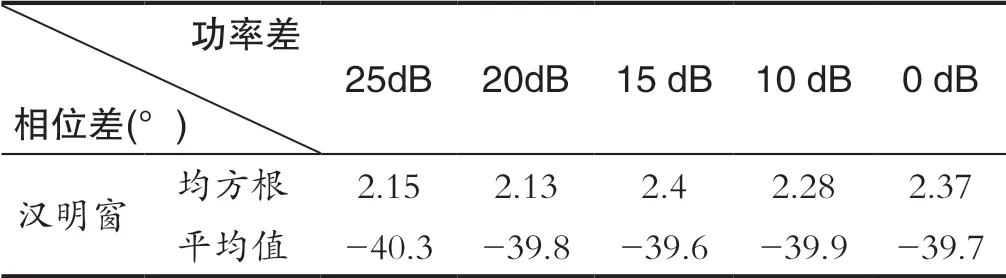
表2 加窗后效果Tab.2 Effect of optimization

2.3 小結

綜上所述，高效相位測量方法僅需要4個乘法器，且與積累時間長度無關，而傳統實現方法中，單個256點的FFT則需要硬件乘法器8個，對于更多點數的FFT處理，資源消耗更大，因此高效測向方法在資源上節省了一倍以上，對于多通道同時多信號的大帶寬無源偵察干涉儀應用而言，這個資源節省效益非常可觀。

從上面的設計還可以看出，利用優化的快速相位測量方法，處理時間消耗為積累點數的一半，而傳統方法則需要消耗積累點數的2.5倍。以256點相位積累時長為例，實際時間消耗僅128個時鐘周期，以62.5MHz為處理主頻時鐘，則單個信號的測相時間為2us，脈沖處理流量可滿足50萬脈沖/秒的高密環境要求。對于更高脈沖流要求，可采用2個或多個并行處理便可實現100萬/秒以上的脈沖流，同樣的性能在傳統方法下需要125MHz或250MHz主頻下進行處理，處理時鐘速率的提高將提高處理難度，同時將指數倍增大器件功耗，系統可靠性將大大下降。

3 結語

本文針對高精度的相位測量進行理論分析，結合工程實現，提出了高效的優化DFT測相方法，資源消耗節約4倍以上，同時處理延遲減小為常規處理方法的1/4，降低了處理時鐘要求，同時提高了脈沖數據的吞吐效率，可在低主頻下完成高密度脈沖信號實時流水處理，極大的降低了系統功耗，提高了系統的可靠性。