Ti3(ZnxAl1-x)C2固溶體熱學、電學和力學性質的理論研究

鄧斐然,徐 敏,苗 峰,黃 毅,馮世全,宋明澤,肖晨達,林園園,李慧敏

(1.西南民族大學電子信息工程國家民委重點實驗室，成都 610041；2.鄭州輕工業大學磁電信息功能材料重點實驗室，鄭州 450002)

0 引 言

MAX相是三元層狀化合物[1-3]，其晶格結構屬于六方晶系，空間群為P63/mmc，分子通式為Mn+1AXn[4-6]，其中M代表過渡族金屬元素，A代表主族元素(通常為ⅢA和ⅣA族元素)，X代表碳或氮，n=1, 2, 3…，當n=2時，分子通式M3AX2稱之為312相材料。過渡金屬M與C或者N組成的Mn+1Xn單元與主族元素A原子面交互迭排，從而構成了獨特的結構，使得MAX相材料具備陶瓷材料和金屬材料的雙重性質[7-8]。MAX相材料不僅具有良好的導電和導熱性，以及高屈服強度抗熱震能力和機械可加工性等性能，而且具有較高的斷裂韌性、熔點和熱穩定性，以及優異的抗氧化和耐腐蝕性等性能[9-11]，同時具有較好的自潤滑性以及相對較低的摩擦系數，這使得該相材料適合應用在高鐵列車、新能源汽車、手機等電子設備以及航天航空等領域。MAX相材料以其獨特良好的性能引起了無數材料工作者的關注和研究[12]。

1994年，Pietzka和Schuster等[13]發現Ti3AlC2材料綜合了金屬和陶瓷的雙重優良性能，具有良好的導電和導熱性、高屈服強度、低硬度、優異的抗氧化和熱穩定性以及高彈性模量導致較好的機械可加工性等。Ti3AlC2材料具有六方層狀結構，由緊密堆積、交替排列的Ti6C八面體層和純Al原子層交互迭排而成，由兩個Ti3AlC2分子構成一個單胞。

2016年，Wang等[11]首先系統地研究了Ti3(SnxAl1-x)C2(x=0, 0.25, 0.5, 0.75, 1)固溶體體系，并分析其結構、能量、穩定性、電學、力學和熱學性質。研究表明:當摻雜了0.75濃度(原子數分數)的Sn原子時，該固溶體體系擁有最大的體積模量；當摻雜了0.5濃度的Sn原子時，該固溶體體系擁有最大的剪切模量。

2019年，李勉等[14]探索合成出Ti3ZnC2，以Ti3AlC2為前驅體，用ZnCl2作為Zn源，通過擁有強路易斯酸性的ZnCl2去腐蝕Ti3AlC2的A層，在一定程度上促使Zn原子進入到A層，導致與Al原子發生完全置換反應，從而得到Ti3ZnC2化合物。測定其晶格常數為a=0.307 4 nm，c=1.860 2 nm。通過彈性常數滿足Born穩定判據得知其力學穩定并結合聲子譜無虛頻可知該研究的Ti3ZnC2結構穩定。這說明在室溫下可以通過材料合成得到Ti3ZnC2相。

目前已發現70多種MAX相材料，這一領域也吸引了越來越多的研究人員，但關于Ti3(ZnxAl1-x)C2的電子結構理論、熱力學理論以及彈性性能相關的研究目前還鮮有報道。國內外關于新型MAX相陶瓷金屬材料的研究主要基于三個方面：(1)MAX相材料合成純度的提高；(2)MAX相材料性能的優化加強；(3)新型MAX相材料的穩定合成[15]。而MAX相的眾多性質都是電子結構性能在起決定性因素,因此探究材料特性最重要的是先研究其電子結構、成鍵特性以及彈性性能[16-19]。本文采用第一性原理的密度泛函理論平面波贗勢法, 通過投影綴加波(PAW)和廣義梯度近似(GGA)對Ti3(ZnxAl1-x)C2固溶體體系進行系統研究，對比并分析其電子結構、成鍵特性和彈性性能的變化趨勢，以及摻雜Zn的濃度對Ti3(ZnxAl1-x)C2固溶體體系性質的影響。

1 計算方法

本文采用基于密度泛函理論(DFT)的PAW對Ti3(ZnxAl1-x)C2(x=0, 0.25, 0.5, 0.75, 1)固溶體體系使用VASP(Vienna Ab-initio Simulation Package)進行模擬理論計算[20]。在本體系的計算中，體系波函數由平面波基組展開，選取PAW描述體系芯電子與離子實間的相互作用，電子與電子間的交換關聯勢選用GGA[21]下的PBE泛函描述[21-22]。動能截斷值在測試后設為520.0 eV，Ti3AlC2和Ti3ZnC2的布里淵區(Brillouin zone)積分k網格采用Gamma為中心的13×13×2取樣方法[23]，Ti3(ZnxAl1-x)C2固溶體體系建立了2×2×1的超胞，其布里淵區積分k點網格采用Gamma為中心的6×6×2取樣方法。同時，為確保在平面波基水平上體系的能量和結構實現收斂，設其自洽精度為10-5eV/atom，原子間相互作用力收斂標準為10-1eV/nm。

2 結果與討論

2.1 電子結構性質

三元層狀化合物Ti3AlC2和Ti3ZnC2晶體結構與其他312型MAX相結構相似，其晶體結構屬于六方晶系，空間群為P63/mmc(No.194)。其中晶體中對應原子的空間占位分別是：Ti1(0,0,0)、Ti2(1/3, 2/3, 0.127)、Al/Zn(0, 0, 1/4)、C(2/3, 1/3, 0.431)。Ti3AlC2和Ti3ZnC2的晶格模型以及Ti3(ZnxAl1-x)C2(x=0.25, 0.5, 0.75)固溶體體系2×2×1超胞的晶格模型如圖1所示，圖1可以看到緊密堆積、交替排列的Ti6C八面體層和Al/Zn原子層交互迭排而構成的六方層狀結構[24]，該層狀結構在層間易于滑移，使其擁有較好的自潤滑性，這對于Ti3(ZnxAl1-x)C2固溶體體系的性質而言有很重要的意義。

通過VASP軟件對Ti3(ZnxAl1-x)C2固溶體體系進行結構優化計算，得到該體系穩定的晶格結構。計算得到優化后的晶格常數和該體系相關的理論值與實驗值列在表1。通過表1可以看出，理論計算值與實驗值均符合得很好，計算結果是可靠的。

本文在進行晶胞結構優化后，得到最穩定狀態下的能量，從而計算出Ti3(ZnxAl1-x)C2固溶體體系的結構模型的形成焓(ΔH)，該公式如下：

ΔH=[Etot(Ti3(ZnxAl1-x)C2, cell)-8xE(Zn)-8(1-x)E(Al)-24E(Ti)-16E(C)]/48

(1)

式中：Etot(Etot(Ti3(ZnxAl1-x)C2, cell)是Ti3(ZnxAl1-x)C2(x=0, 0.25, 0.5, 0.75, 1)固溶體每個體系最穩定狀態下的總能量，則E(Ti)、E(Zn)、E(Al)和E(C)分別是Ti、Zn、Al和C結構晶胞中單個原子最穩定狀態下的能量。得到的結構模型的形成焓(ΔH)對于判斷材料是否擁有良好的熱力學穩定是必不可少的條件。從表1中可以看到，其值均為負數，這表明Ti3(ZnxAl1-x)C2固溶體體系的結構模型均是符合熱力學穩定的。

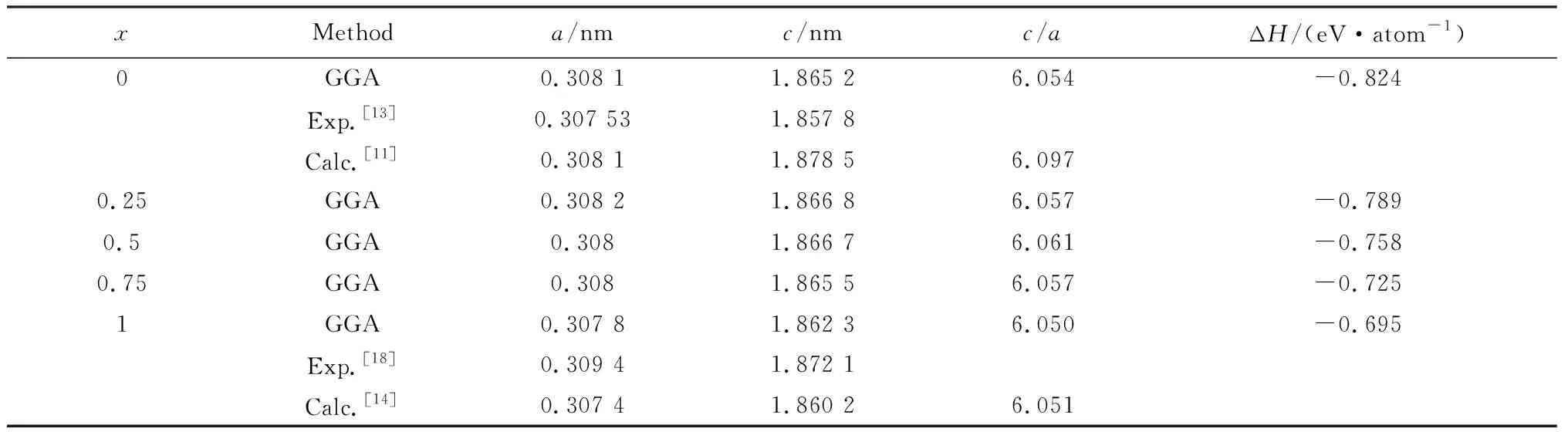
表1 Ti3(ZnxAl1-x)C2(x=0, 0.25, 0.5, 0.75, 1)固溶體的晶格常數和晶格形成焓Table 1 Lattice parameters and enthalpy formation energy for Ti3(ZnxAl1-x)C2 (x=0, 0.25, 0.5, 0.75, 1) solid solutions

為了解釋Ti3(ZnxAl1-x)C2固溶體結構的本征穩定性，在優化后的晶胞結構的基礎上，通過VASP的DFPT方法計算該材料的聲子色散關系[25]。聲子色散關系圖解釋聲子頻率在布里淵區內沿著高對稱點方向的晶格振動譜，其橫坐標是布里淵區的高對稱點，縱坐標是經過每個高對稱點的聲子振動頻率。從圖2可以看出，聲子色散的頻率在整個布里淵區內都是在零點(0 THz)以上的，即沒有虛頻(負頻)出現，預示著該晶體結構具有本征值穩定性，這也代表著Ti3(ZnxAl1-x)C2固溶體體系的結構模型是符合動力學穩定的。除此之外，在聲子色散關系圖中G點附近的光學分支的聲子頻率均有不同，導致離子鍵存在于在該晶體中；并且可以看到在M-K和H-L區間有兩個對應著聲子色散關系圖中平緩的帶，說明在這個位置產生了局域化特征，使其產生強烈的晶格振動。

圖2 Ti3(ZnxAl1-x)C2(x=0, 0.25, 0.5, 0.75, 1)固溶體的聲子色散關系Fig.2 Phonon dispersion spectra of Ti3(ZnxAl1-x)C2 (x=0, 0.25, 0.5, 0.75, 1) solid solutions

在晶胞結構優化的基礎上，對Ti3(ZnxAl1-x)C2固溶體進行了電子結構方面的計算，得到總態密度(TDOS)和分波態密度(PDOS)。圖3可以看出Ti3(ZnxAl1-x)C2固溶體體系的態密度分布情況。Ti3(ZnxAl1-x)C2(x=0)的TDOS圖可分為4個主峰，隨著Zn原子摻雜濃度的增加，TDOS圖逐漸出現第五個峰。其中在導帶中只有一個峰PⅠ，而在價帶中有PⅡ、PⅢ和PⅣ三個峰。當有Zn原子摻雜時出現第五個峰PⅤ，其中在-12.4～-8.2 eV能量區間出現的PⅡ主要來自C原子2s軌道電子的貢獻，少部分來自Ti原子3d軌道電子；在-5.9～-1.7 eV能量區間出現的PⅢ峰主要來自Ti原子3d軌道電子、Al原子3p軌道電子和C原子2p軌道電子的雜化作用。但隨著Zn原子摻雜比例的增加，Al原子3p軌道電子的貢獻在逐漸降低，這表明Ti原子和C原子之間結合成鍵具有很強的共價鍵，從而導致了該固溶體的結構模型是穩定的；在價帶頂-1.7～0 eV能量區間出現的PⅣ主要是來自Ti原子3d軌道電子和Al軌道電子3p的雜化作用；在位于導帶0～4.2 eV能量區間出現的PⅣ峰主要來自Ti原子3d軌道電子的貢獻，而Al原子3p軌道電子和C原子2p軌道電子的貢獻相對非常少；在Zn原子的摻雜下，-7.4～-6 eV能量區間出現的PⅤ峰幾乎都是來自Zn原子3d軌道電子的貢獻，其能量值與Zn原子摻雜濃度成正比。該固溶體費米面的位置是在0 eV能量值處，其電子態密度計算值N(EF)都大于0，主要來自Ti原子3d軌道電子的貢獻，表明電子較容易得到能量躍遷到導帶，從而有像金屬一樣的導電特性，呈金屬性。同時隨著摻雜Zn原子濃度的增加，費米面偏移向了更高能級區域，使得在費米能級處的電子態密度值逐漸增大，Ti3(ZnxAl1-x)C2(x=0, 0.25, 0.5, 0.75, 1)固溶體其值依次為16.65 eV、19.09 eV、20.86 eV、22.65 eV、23.06 eV，其導電性能也在依次增強，其中Ti3ZnC2的導電性能是最強的。

圖3 Ti3(ZnxAl1-x)C2(x=0, 0.25, 0.5, 0.75, 1)固溶體的總態密度(TDOS)和分波態密度(PDOS)圖Fig.3 Calculated total DOS and PDOS of Ti3(ZnxAl1-x)C2 (x=0, 0.25, 0.5, 0.75, 1) solid solutions

為了得到Ti3(ZnxAl1-x)C2固溶體更加詳盡的化學鍵情況，計算了該固溶體的電子局域函數(ELF)，并選取各個晶胞(110)面進行分析。圖4可以看出，在Ti和C原子之間的電子局域函數更傾向于C原子，這也說明了C原子易得到電子而Ti原子易失去電子，從而表明Ti—C鍵之間是強共價鍵和離子鍵的結合，使其具有陶瓷材料的高強度、高模量和高熔點。在Ti和Zn原子以及Ti和Al原子的中間，它的電子局域函數接近于0.5，這說明Ti—Zn和Ti—Al鍵是具有金屬鍵特性的。同時可以看出其具備共價鍵和金屬鍵成分，這使得該固溶體具有金屬材料的延展性和導電性。

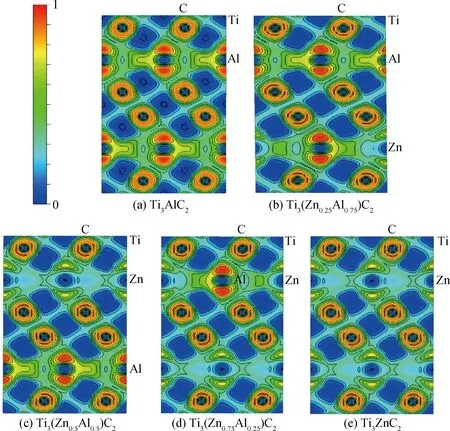
圖4 Ti3(ZnxAl1-x)C2(x=0, 0.25, 0.5, 0.75, 1)固溶體的電子局域函數Fig.4 Electronic local area functions of Ti3(ZnxAl1-x)C2 (x=0, 0.25, 0.5, 0.75, 1) solid solutions

通過VASP計算和VTST的腳本處理得到的Bader電荷，能夠更加詳細地分析電子的轉移情況，表2可以看出各個原子得失電子的情況。Ti原子失去電子使其帶正電荷，并且由于Ti1和Ti2原子在結構中的位置不同，這導致失去電子的數量也會有差別；Al和Zn原子以及C原子得到電子使其帶負電荷，因此，Ti3(ZnxAl1-x)C(x=0, 0.25, 0.5, 0.75, 1)固溶體均具有共價鍵和離子鍵以及金屬鍵的綜合特性。還看到Ti和C的總Bader電荷幾乎是恒定的。Al和Zn的總Bader電荷從28.904增加到101.416，這說明隨著Zn原子摻雜濃度的增加，Zn原子得到的電子隨之增加，導致了總電子數也隨之增加，這對Ti3(ZnxAl1-x)C2固溶體體系的晶格參數有本質的影響。

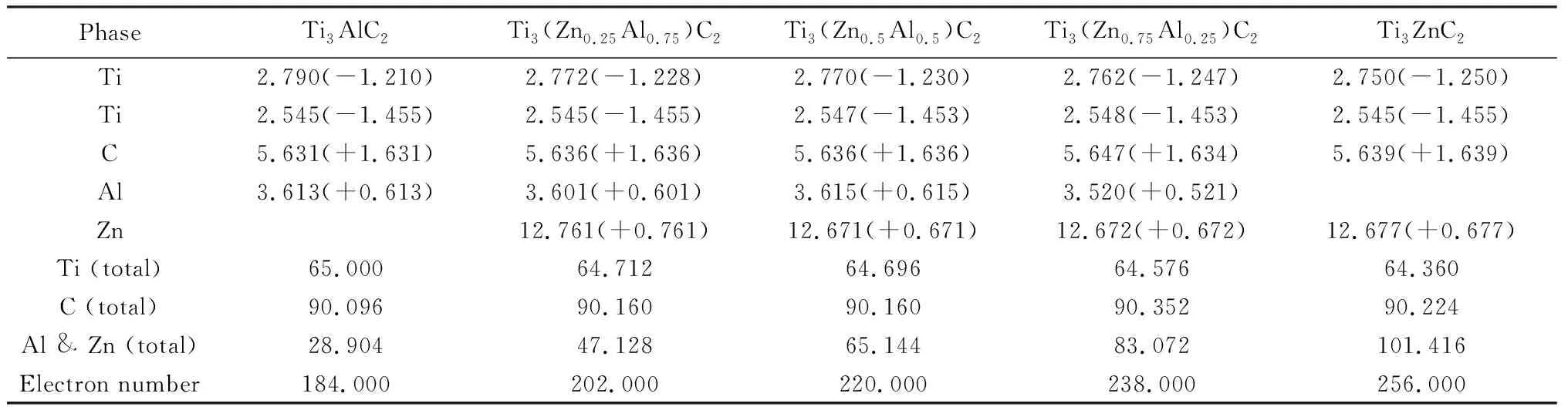
表2 Ti3(ZnxAl1-x)C2(x=0, 0.25, 0.5, 0.75, 1)固溶體的Bader電荷分析Table 2 Bader charge analysis of Ti3(ZnxAl1-x)C2 (x=0, 0.25, 0.5, 0.75, 1) solid solutions

2.2 彈性性質

在優化后的晶胞結構的基礎上，進一步研究了Ti3(ZnxAl1-x)C2固溶體體系的力學特性，通過VASP計算得到該材料的彈性常數和彈性模量分別列在表3中，根據Born和Huang力學穩定性判據[26]對該六方晶系的五個獨立的彈性常數(C11、C33、C44、C12、C13)列出以下穩定性條件：

(2)

由表3可知，Ti3(ZnxAl1-x)C2固溶體體系均滿足穩定性條件，可以證明Ti3(ZnxAl1-x)C2固溶體均是力學穩定性材料。

利用彈性常數可以研究具有六方晶體結構的Ti3(ZnxAl1-x)C2固溶體體系的彈性各向異性[27]，普遍使用以下三個參數來進行判定：

(3)

式中：ΔP表示材料壓縮波的各向異性情況，而ΔS1和ΔS2表示材料剪切波的各向異性情況。當它們得出的參數值都不為1時，該材料的彈性是各向異性的。從表3可知該材料均表現為各向異性的情況。其中彈性常數C11和C33遠高于C44，這說明該固溶體的單向變形阻力遠高于剪切變形阻力。采用Vogit-Reuss-Hill近似計算得到體模量(B)、剪切模量(G)和楊氏模量(E)等。其中體模量是衡量材料抵抗體積變化的能力，是抵抗斷裂的能力；剪切模量是衡量材料抵抗形狀變化的能力，是抵抗塑性變形的能力。這兩個模量的比值(G/B)是Pugh提出的一個經驗判據，可以用來預測材料的脆韌性[28]。從表3中可以看出其值都大于0.57，預示著Ti3(ZnxAl1-x)C固溶體體系都為脆性。除此之外，泊松比σ作為衡量脆韌性的另一個判據，其值均小于1/3，說明了其都為脆性，這與G/B經驗判據的結論一致。但隨著摻雜Zn原子濃度的增加，G/B逐漸接近于經驗判據中韌塑性的臨界值,這表明了該固溶體的韌性有逐步增強的趨勢。

表3 Ti3(ZnxAl1-x)C2(x=0, 0.25, 0.5, 0.75, 1)固溶體的各向異性參數(ΔP、ΔS1、ΔS2)，彈性常數Cij和彈性模量Table 3 Anisotropy parameters (ΔP, ΔS1, ΔS2)， calculated elastic constants Cij and elastic moduli for Ti3(ZnxAl1-x)C2 (x=0, 0.25, 0.5, 0.75, 1) solid solutions

3 結 論

本文采用基于密度泛函理論的投影綴加平面波方法，系統地對Ti3(ZnxAl1-x)C2(x=0, 0.25, 0.5, 0.75, 1)固溶體體系進行VASP模擬理論計算和性質分析。通過研究表明：計算得到的形成焓均小于零，符合熱力學穩定；結合聲子色散關系圖，可知其均具有本征值穩定性，符合動力學穩定；根據彈性常數滿足Born穩定判據，符合力學穩定。對于電子結構性質，費米能級處電子態密度值N(EF)均大于0，主要來自Ti原子3d軌道電子的貢獻，表明該材料均具有導電能力，呈金屬性。同時隨著摻雜Zn原子濃度的增加，費米面偏移向了更高能級區域，使得在費米能級處的電子態密度值逐漸增大，這使得導電性能也在依次增強，其中Ti3ZnC2的導電性能是最強的。在電子局域函數圖和Bader電荷的結合下，可以得到該材料均具有共價鍵和離子鍵以及金屬鍵的綜合特性。對于彈性性質，分析得出其彈性均是各向異性的，并且該固溶體各濃度下均為脆性。但隨著摻雜Zn原子濃度的增加，G/B逐漸接近于經驗判據中韌塑性的臨界值,表明該固溶體的韌性有逐步增強趨勢。本文研究了Ti3(ZnxAl1-x)C2(x=0, 0.25, 0.5, 0.75, 1)固溶體體系主要的物理性質，這一系列的研究結果希望能為今后的實驗和理論研究提供參考。