基于勒讓德多項(xiàng)式逼近的鉆孔巖性分布特征預(yù)測(cè)模型

王權(quán)銘 楊宇江，2 路增祥，2 馬 馳 曹 朋

(1.遼寧科技大學(xué)礦業(yè)工程學(xué)院，遼寧 鞍山 114051;2.遼寧省金屬礦產(chǎn)資源綠色開采工程研究中心，遼寧 鞍山 114051;3.北京科技大學(xué)土木與資源工程學(xué)院，北京 100083)

穿孔作業(yè)是露天礦山開采中高耗能、高耗時(shí)的生產(chǎn)工序[1-6]，縮短穿孔作業(yè)時(shí)間是提高礦山生產(chǎn)效率、降低生產(chǎn)成本的有效措施之一。礦巖的物理力學(xué)特性及其分布特征對(duì)于確定穿孔位置、間排距等炮孔設(shè)計(jì)參數(shù)，選擇鉆機(jī)鉆頭，調(diào)整鉆速和鉆壓等影響重大[7-9]，且直接影響著鉆機(jī)的穿孔速度，進(jìn)而影響了礦山的開采效率[10-12]。準(zhǔn)確預(yù)測(cè)采場(chǎng)巖性及其分布特征能夠?yàn)榈V山穿孔爆破設(shè)計(jì)工作提供基礎(chǔ)資料，也能幫助鉆機(jī)操作人員預(yù)判穿孔位置礦巖的可鉆性，更好地操控鉆機(jī)作業(yè)[13-15]，以縮減穿孔時(shí)間，提高礦山開采效率。

為研究精確可靠的巖性預(yù)測(cè)方法，劉向君等[16]提出了以神經(jīng)網(wǎng)絡(luò)技術(shù)為基礎(chǔ)的巖石強(qiáng)度預(yù)測(cè)方法;王棣等[17]采用神經(jīng)網(wǎng)絡(luò)BP算法建立了能夠估計(jì)二維地震剖面的地層巖性預(yù)測(cè)方法;曹正林等[18]認(rèn)為鉆井參數(shù)與巖性有直接或間接的關(guān)系，據(jù)此可在鉆進(jìn)過程中隨時(shí)了解地下巖層情況。張建林等[19]根據(jù)波阻抗與巖性之間具有一定的概率相關(guān)關(guān)系，綜合應(yīng)用多學(xué)科信息，建立了預(yù)測(cè)巖性圈閉隨機(jī)模擬方法。劉向君等[20]針對(duì)在室內(nèi)常溫常壓下進(jìn)行巖石微可鉆性試驗(yàn)存在的可鉆性數(shù)據(jù)離散、隨機(jī)、有限、成本高等問題，采用物理模型方法推導(dǎo)出利用了聲波測(cè)井資料預(yù)測(cè)巖石可鉆性的計(jì)算模型，并結(jié)合S油田實(shí)際資料開展了鉆速預(yù)測(cè)方法研究。此外，支持向量機(jī)[21]、灰色理論[22]也被應(yīng)用于巖性預(yù)測(cè)工作中。上述研究大多采用機(jī)器學(xué)習(xí)方法對(duì)巖性進(jìn)行預(yù)測(cè)，雖然該類方法可以從變動(dòng)的樣本數(shù)據(jù)中進(jìn)行動(dòng)態(tài)學(xué)習(xí)，但所需鉆孔數(shù)據(jù)量較大，有時(shí)需要人為建立某種模型對(duì)其進(jìn)行指數(shù)倍的篩選，使得該類方法應(yīng)用存在一定的局限性。

上述研究在促進(jìn)巖性預(yù)測(cè)發(fā)展方面具有重要價(jià)值，但大多是圍繞石油勘探鉆井問題展開，針對(duì)金屬礦山露天采場(chǎng)巖性預(yù)測(cè)的研究涉及較少。本研究以最佳函數(shù)逼近法為基礎(chǔ)，采用勒讓德多項(xiàng)式建立金屬礦山露天采場(chǎng)的巖性預(yù)測(cè)模型，利用有限的鉆孔巖性分布特征信息，預(yù)測(cè)待穿孔位置的礦巖分布特征，為礦山穿爆設(shè)計(jì)和穿孔施工提供依據(jù)。

1 基本原理

1.1 函數(shù)逼近法

函數(shù)逼近法是一種應(yīng)用較廣泛的函數(shù)擬合方法[23]。使用該方法建立預(yù)測(cè)模型時(shí)既不需要大量的數(shù)據(jù)進(jìn)行推導(dǎo)，也不需要根據(jù)特定模型進(jìn)行處理，具有簡單、靈活等特點(diǎn)。

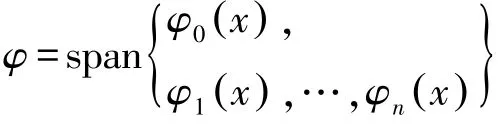
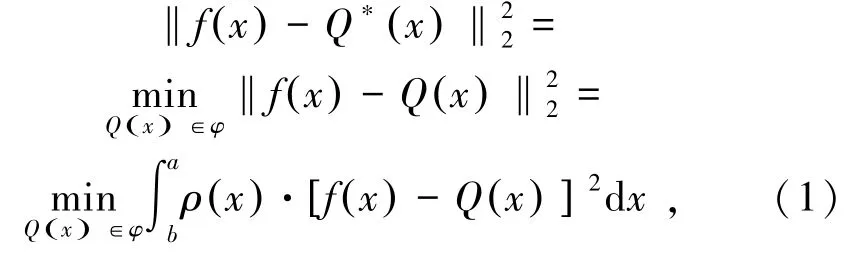
式中，C[a，b]表示在[a，b]上連續(xù)的全體函數(shù)組成的集合;span{·}為向量張成的線性空間;Q*(x)為f(x)在子集φ∈C[a，b]中的最佳平方逼近多項(xiàng)式;ρ(x)為權(quán)函數(shù)。

式(1)等價(jià)于求多元函數(shù)I(a0，a1，…，am)的最小值，其最小值為

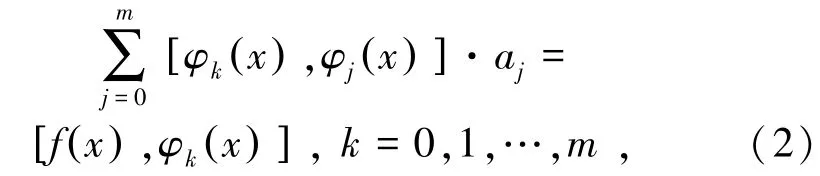
式中，aj為回歸系數(shù);I(a0，a1，…，am)為關(guān)于a0，a1，…，am的二次函數(shù);m表示m元函數(shù)。

式(2)是關(guān)于aj(j=0，1，…，m)的線性方程組。設(shè)φ0(x)，φ1(x)，…，φm(x)是權(quán)函數(shù)ρ(x)的正交函數(shù)族，得到

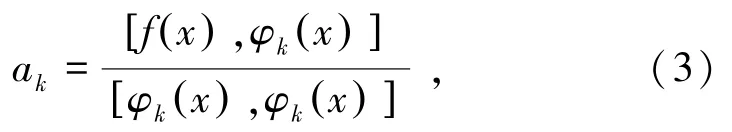
式中，ak代表第k個(gè)線性方程組的回歸系數(shù);[f(x)，φk(x)]表示首項(xiàng)系數(shù)為1的最大公約式。

1.2 勒讓德多項(xiàng)式

勒讓德多項(xiàng)式是權(quán)函數(shù)ρ(x)≡1在區(qū)間[-1，1]上由{1，x，…，xn}正交化得到的多項(xiàng)式[24]:

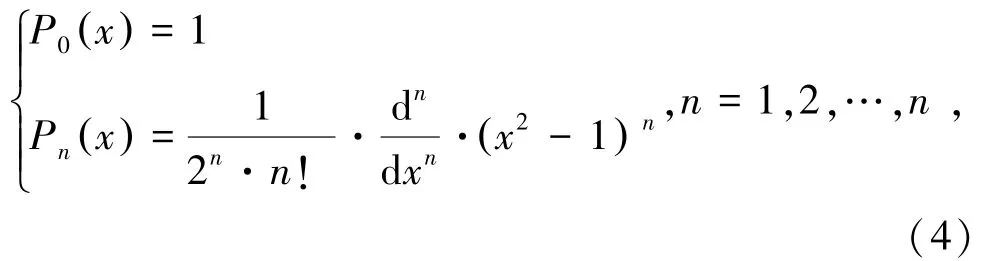
式中，n為階數(shù)。

作為一種正交多項(xiàng)式，勒讓德多項(xiàng)式具有系數(shù)之間相互獨(dú)立的特點(diǎn)，其正交對(duì)數(shù)矩陣具有較小的偶然性且只會(huì)影響其中的某一項(xiàng)，使用勒讓德多項(xiàng)式預(yù)測(cè)可以極大地減少誤差。因此該方法被廣泛用于預(yù)測(cè)模型構(gòu)建、誤差分析、參數(shù)選擇等方面[25]。

2 巖性分布特征預(yù)測(cè)模型

露天礦穿孔作業(yè)過程中，會(huì)遇到具有不同力學(xué)特征的礦巖體。根據(jù)礦巖特性的不同，適時(shí)調(diào)整鉆機(jī)的鉆速及鉆壓，有利于提高穿孔速度。根據(jù)先期地質(zhì)鉆孔所揭露的地層特征信息，建立待穿孔位置的礦巖層巖性預(yù)測(cè)模型，對(duì)于預(yù)判礦巖分布特征具有重要的工程意義。

將已知的鉆孔地層特征作為樣本信息，以最佳函數(shù)逼近法為基礎(chǔ)，采用勒讓德多項(xiàng)式建立穿孔位置的巖性預(yù)測(cè)模型，流程如圖1所示。

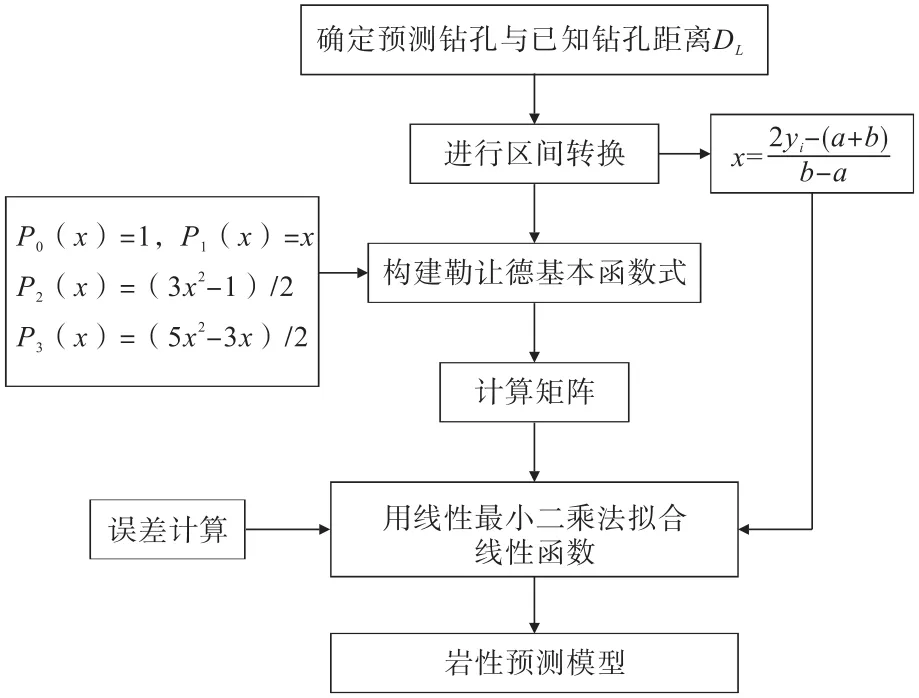
圖1 基于勒讓德多項(xiàng)式的巖性預(yù)測(cè)建模流程Fig.1 Thology prediction modeling process based on Legendre polynomial

對(duì)已知鉆孔穿過的各巖層依次記為yi，則區(qū)間變換表達(dá)式為

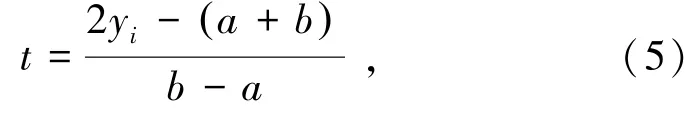
式中，t為勒讓德變量;yi為鉆孔的層段編號(hào)，i=1，2，…，n;a為巖層最頂端標(biāo)高;b為某巖層的底面標(biāo)高。

此時(shí)，t取值處于[-1，1]區(qū)間，相應(yīng)的概率密度為f(yi)，其均值M0和原點(diǎn)矩MK可進(jìn)行如下計(jì)算:

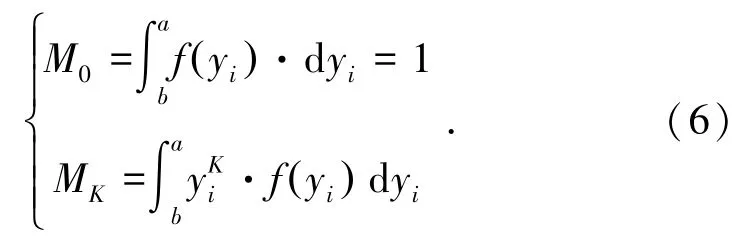
根據(jù)辛欽大數(shù)定律[24]，原點(diǎn)矩和K階原點(diǎn)矩相等，即

式中，AK表示K階原點(diǎn)矩。

由于勒讓德多項(xiàng)式具有正交性和奇偶性，由其遞推公式可得到:

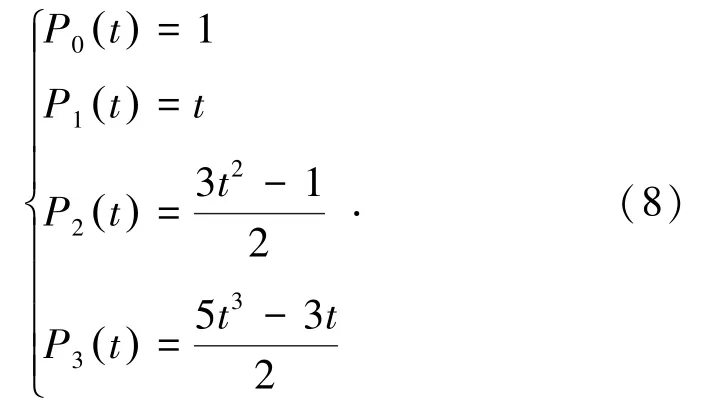
以勒讓德多項(xiàng)式進(jìn)行幾何參數(shù)化建模，用λ表示第i個(gè)鉆孔基于勒讓德多項(xiàng)式的誤差值進(jìn)行建模。對(duì)勒讓德多項(xiàng)式以λ為基函數(shù)進(jìn)行展開，得到:

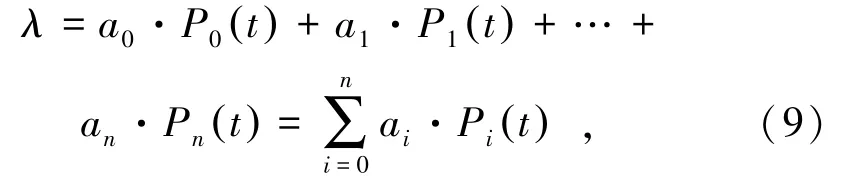
式中，a0、a1、…、an為回歸系數(shù)。

用最小二乘法展開式(9)得到:

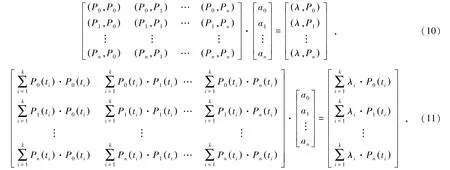
式中，k為鉆孔穿越巖層的總層位數(shù);i表示第i個(gè)鉆孔;λi為第i個(gè)鉆孔基于勒讓德多項(xiàng)式的誤差值;ti表示第i個(gè)鉆孔勒讓德變量值;Pn(ti)表示n階勒讓德多項(xiàng)式值。

由式(4)與式(9)可得到如下預(yù)測(cè)模型:

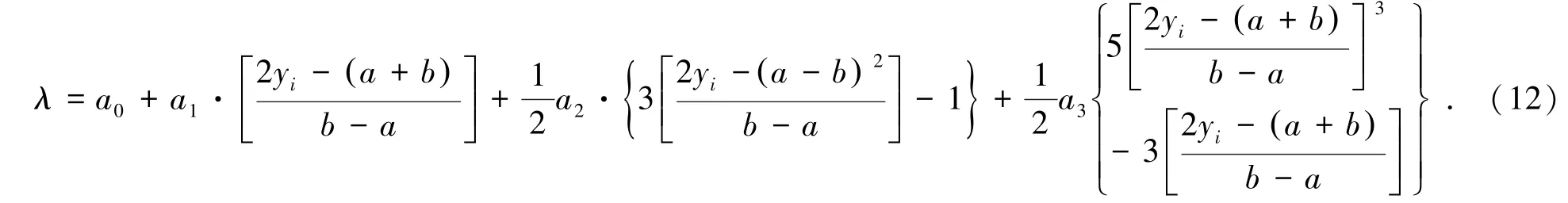
簡化式(12)，可得到:

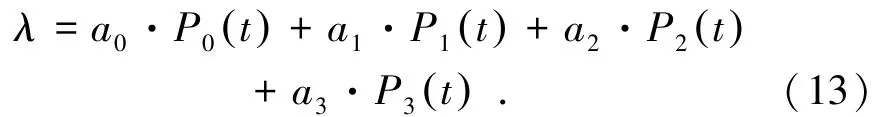
則預(yù)測(cè)誤差值δ可進(jìn)行如下計(jì)算:

式中，DL為預(yù)測(cè)鉆孔與某一個(gè)已知鉆孔間的直線距離。

3 預(yù)測(cè)模型可靠性驗(yàn)證

3.1 基礎(chǔ)鉆孔資料

根據(jù)某鉛鋅礦床的ZK2201和ZK4201鉆孔數(shù)據(jù)，驗(yàn)證預(yù)測(cè)模型的可靠性。兩鉆孔所揭露的巖層分布特征見表 1。ZK2201、ZK4201鉆孔和預(yù)測(cè)鉆孔ZK3201的位置關(guān)系如圖2所示。

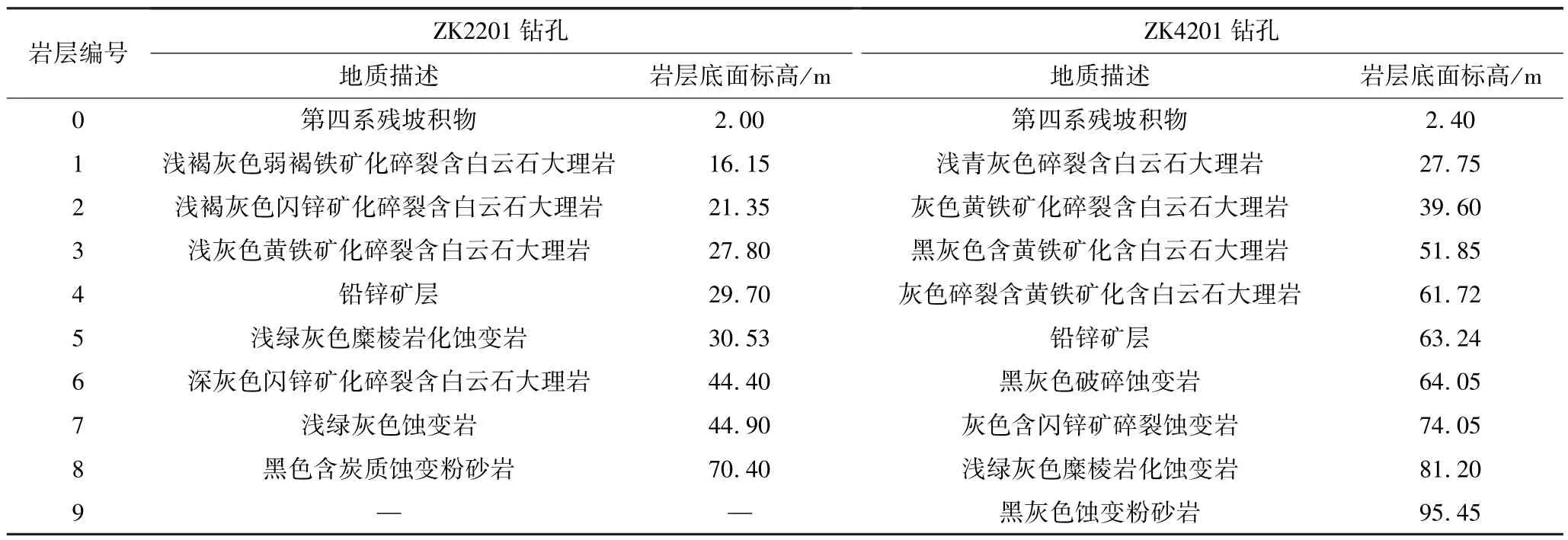
表1 ZK 2201、ZK 4201鉆孔位置的巖層信息Table 1 Rock stratum information of ZK 2201 and ZK 4201 drilling hole

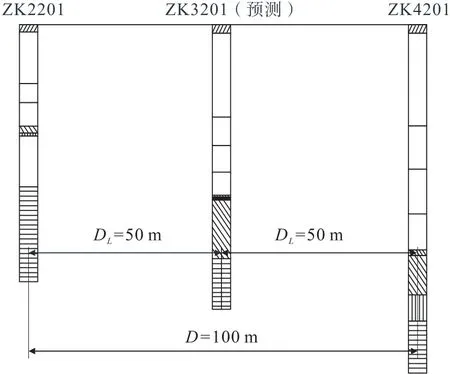
圖2 預(yù)測(cè)鉆孔與基礎(chǔ)鉆孔巖性及厚度對(duì)比Fig.2 Comparison of lithology and thickness between predicted borehole and base boreholes

3.2 待穿孔位置巖層特征信息預(yù)測(cè)

以待穿孔鉆孔位于ZK2201和ZK4201鉆孔正中間為例(該處實(shí)際存在ZK3201鉆孔，為驗(yàn)證預(yù)測(cè)結(jié)果的可靠性，假定其巖層信息未知)，根據(jù)表1給出的已知鉆孔巖層特征信息，采用建立的模型預(yù)測(cè)待鉆鉆孔的巖層信息。

根據(jù)表1中各巖層的厚度，采用式(11)、式(12)、式(14)計(jì)算，可得到待穿孔處對(duì)應(yīng)的巖層厚度誤差及對(duì)應(yīng)的勒讓德多項(xiàng)式函數(shù)值見表2。

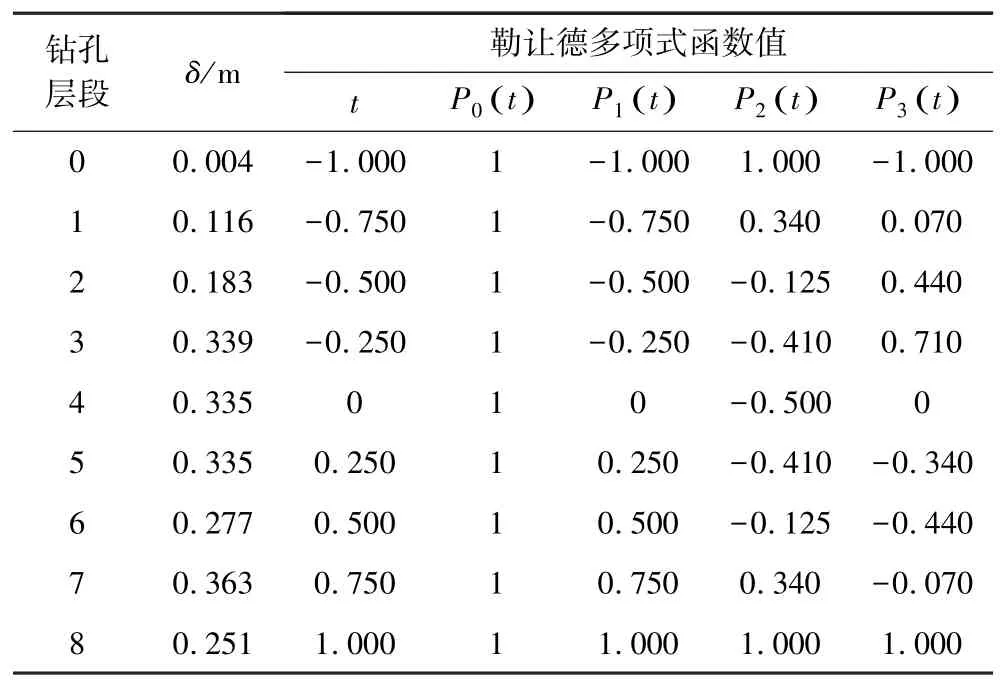
表2 待穿孔處對(duì)應(yīng)誤差及勒讓德多項(xiàng)式函數(shù)值Table 2 Corresponding errors and Legendre polynomials function values at the hole to be drilled

對(duì)表2，根據(jù)式(11)取k=9，n=3(勒讓德階數(shù))，建立矩陣關(guān)系式:

對(duì)式(15)求解，得到對(duì)應(yīng)的回歸系數(shù)為a0=0.259 7，a1=0.118 4，a2=-0.131 4，a3=0.028 4。

根據(jù)計(jì)算式(13)得到的回歸系數(shù)，由預(yù)測(cè)模型建立待穿孔處的勒讓德基函數(shù)的誤差擬合多項(xiàng)式模型:

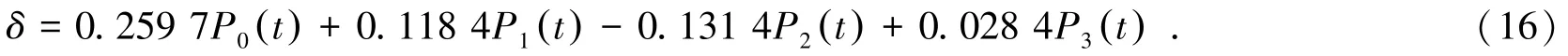
根據(jù)式(8)和表2，由式(16)可得到:

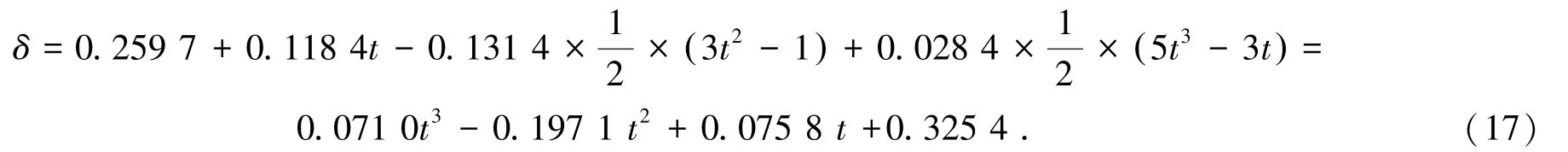
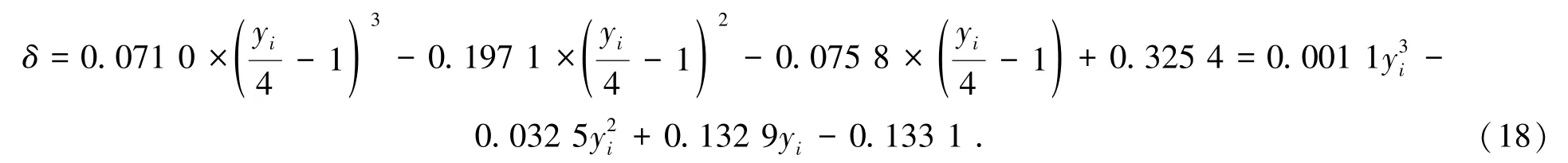
根據(jù)表1，取層段最小值為待預(yù)測(cè)層段數(shù)量，為9 個(gè)層段，即i=0，1，2，…，8。對(duì)式(18)賦予不同的值，每隔1層段將2次鉆孔數(shù)據(jù)進(jìn)行一次比較，可計(jì)算出待穿孔位置處不同巖層的厚度。結(jié)合ZK2201鉆孔和ZK4201鉆孔巖性柱狀圖，根據(jù)表1及待穿孔處巖性預(yù)測(cè)結(jié)果，得到預(yù)測(cè)鉆孔與基礎(chǔ)鉆孔的巖性及其厚度對(duì)比如圖2所示。

3.3 預(yù)測(cè)結(jié)果

將待穿孔位置的巖性特征預(yù)測(cè)結(jié)果與該位置的實(shí)際鉆孔(ZK3201)巖性特征信息進(jìn)行了對(duì)比，結(jié)果見表3。

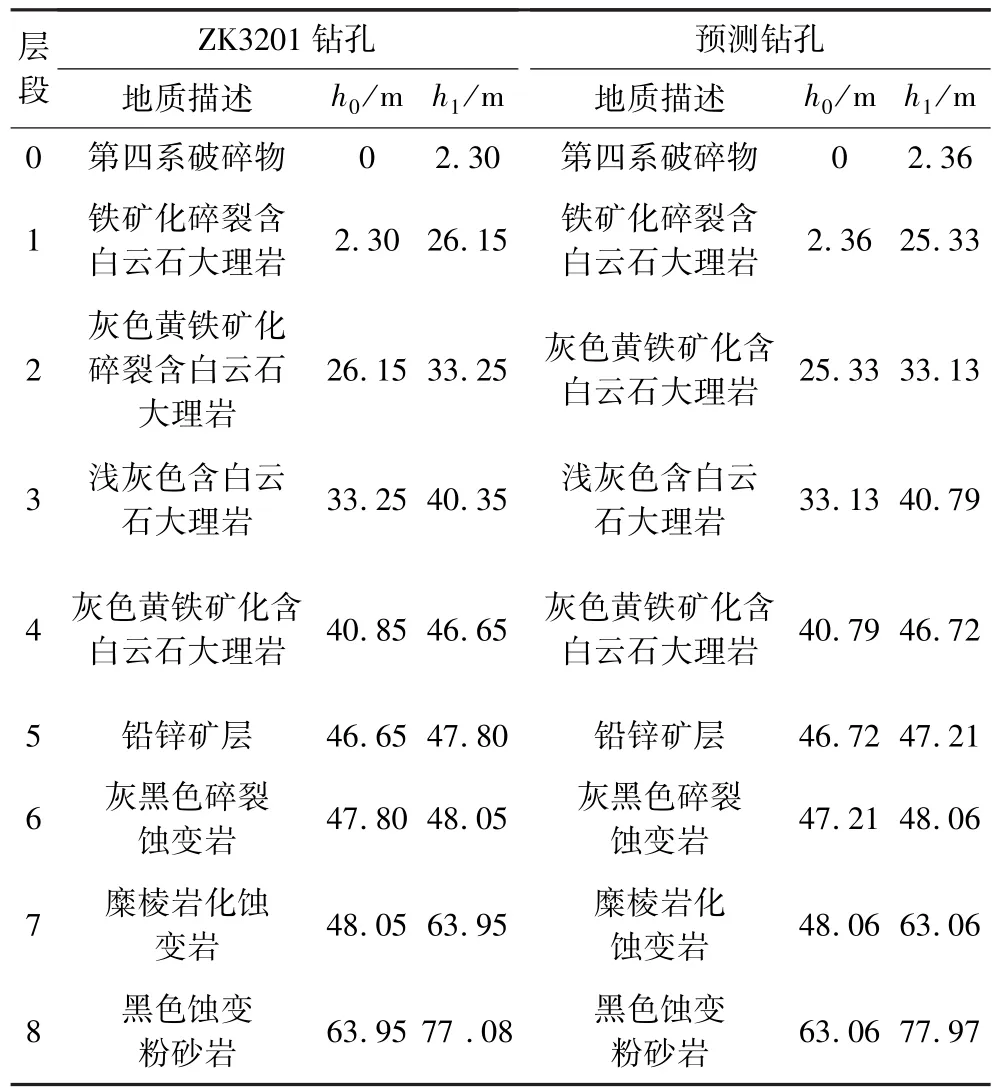
表3 待穿孔位置巖性特征預(yù)測(cè)結(jié)果與實(shí)際ZK 3201鉆孔信息對(duì)比Table 3 Comparison of lithological feature prediction results of the position to be drilled with information of actual ZK 3201 drilling hole

由表3可知:預(yù)測(cè)的巖性厚度與標(biāo)高分布與該處的實(shí)際鉆孔信息基本相同，預(yù)測(cè)結(jié)果與實(shí)際信息誤差相對(duì)較小，如圖3所示。

預(yù)測(cè)誤差大小與基礎(chǔ)鉆孔的數(shù)量、間距以及預(yù)測(cè)鉆孔與某一個(gè)已知鉆孔間的直線距離大小相關(guān)。由圖3可知:在本研究給定條件下，由于自然界巖體在空間展布上的不均勻性和復(fù)雜性，基礎(chǔ)鉆孔數(shù)量僅有2個(gè)且相距較遠(yuǎn)，采用勒讓德多項(xiàng)式建立的鉆孔巖性預(yù)測(cè)模型對(duì)待預(yù)測(cè)位置處的鉆孔巖性進(jìn)行預(yù)測(cè)，最大誤差為3.12%，總體誤差相對(duì)較小。在礦山實(shí)際穿孔作業(yè)中，當(dāng)炮孔距離較小(一般為2.5～4.5 m)，且可利用的鉆孔信息較多時(shí)，本研究方法的預(yù)測(cè)誤差會(huì)進(jìn)一步減小。采用本研究方法進(jìn)行鉆孔巖性分布預(yù)測(cè)，在一定程度上可以滿足礦山穿孔作業(yè)需要。

4 結(jié) 論

(1)構(gòu)建了基于勒讓德多項(xiàng)式的待鉆孔位置的巖性分布特征預(yù)測(cè)模型。該模型以勒讓德多項(xiàng)式為基礎(chǔ)，結(jié)合概率密度多項(xiàng)式函數(shù)逼近法，通過建立鉆孔信息與鉆孔距離之間的關(guān)系計(jì)算誤差范圍，在獲得兩個(gè)鉆孔數(shù)據(jù)的情況下，即可預(yù)測(cè)出兩個(gè)鉆孔間任意位置處待穿孔位置的巖層分布特征。

(2)采用礦山實(shí)際鉆探鉆孔信息數(shù)據(jù)驗(yàn)證了所建預(yù)測(cè)模型的準(zhǔn)確性。結(jié)果表明:預(yù)測(cè)最大誤差為3.12%，能夠滿足露天礦山穿孔作業(yè)對(duì)巖性預(yù)測(cè)的需要，有助于實(shí)現(xiàn)穿孔作業(yè)智能控制，提高鉆機(jī)穿孔效率。

(3)本研究構(gòu)建的模型對(duì)于層狀分布的巖層(如煤系)有較好的適用性，但由于勒讓德多項(xiàng)式的局限性，后期仍需進(jìn)一步優(yōu)化模型，提高其普適性。