“人”字形曲線高架橋地震動多角度輸入研究

畢研超

（濟南市交通工程質量與安全中心，山東濟南 250014）

1 引言

“人”字形曲線高架橋有直線段、變截面段以及曲線段，是曲線高架橋的典型代表，結構形式和受力復雜。目前，國內一、二線城市高架橋的建設與日俱增，三線城市高架橋建設正在崛起，曲線高架橋的應用甚為廣泛。我國是地震多發國家，亟需對“人”字形曲線高架橋抗震體系展開研究，分析“人”字形曲線高架橋在地震發生時的最不利地震動反應，對于抗震設防和維修加固具有重要意義，同時也可為發生地震后抗震救災工作打下基礎。

地震動最不利輸入方向確定標準包括2種：結構響應達到峰值；結構局部截面達到屈服。本文主要采用第一種，地震動輸入時哪個位置的響應達到峰值即確定該處為不同角度輸入時的最不利地震動位置。

2 有限元分析模型

某城市曲線高架橋，直線總跨徑為72 m，橋面由1 片變截面主梁（1#梁）與2片等截面分支梁（2#梁、3#梁）組成，其中1#主梁與2#分支梁為直線梁，3#分支梁為曲線梁，橋梁整體平面呈“人”字形式，如圖1所示。墩高30 m，主梁與橋墩截面如圖2所示。

圖1 “人”字形曲線高架橋

圖2 主梁與橋墩截面（單位：cm ）

建立MIDAS有限元分析模型，模型結構縮尺比為 1/20，如圖3所示。其中1#墩、2#墩、5#號墩墩頂設置固定支座，其余墩頂設置活動支座，模型不考慮樁土相互作用，橋墩底部固結，不考慮橋臺與土的相互作用。

圖3 “人”字形曲線高架橋有限元模型

3 地震動多角度輸入

模型選用EI centro波，采用一致激勵輸入進行有限元分析，EI centro波峰值加速度為 197.32 gal，如圖4所示。曲線高架橋坐標系如圖5所示。

圖4 EI centro波

根據圖5可列以下算式：

圖5 曲線高架橋坐標

式（1）、式（2）中，x為梁的切線方向；y為梁的徑線方向；X為地震波輸入方向；Y為地震波輸入方向的徑線方向； 為X方向與y方向之間的夾角。

本文中地震波的輸入方向只需從0°輸入到180°，每隔30°輸入一次。而最不利地震動方向為輸入地震波時不同位置x方向和y方向的最大值。

4 結果分析

4.1 墩頂 x 向位移分析

墩頂x向位移如表1所示。由表可知，在地震動沿X向橋梁縱向輸入時，即直線梁X與x一致， 為0°時，0°與180°正向及反向輸入墩頂位移一致，2#墩頂位移在所有橋墩位移中最大，最易發生落梁現象，而地震動輸入方向為90°時位移最小。所有數據中，2#墩頂位移在X向地震動作用下明顯大于其他墩頂位移，因此，在實際施工過程中主要考慮X向地震動輸入時2#墩頂位移即可。

表1 墩頂x向位移 m

4.2 墩頂 y 向位移分析

墩頂y向位移如表2所示。由表可知，在地震動沿Y向橋梁橫向輸入時，即直線梁Y與y一致， 為90°時，1#、2#、3#以及4#墩頂位移達到最大值，地震動輸入方向為60°時，5#和6#墩頂位移達到最大值，而1#墩頂在所有墩中位移最大，最易發生落梁現象。 0°與180°正向及反向輸入時墩頂位移一致。所有數據中，1#墩頂位移在Y向地震動作用下明顯大于其他墩頂位移，因此，在實際施工過程中主要考慮Y向地震動輸入時1#墩頂位移即可。

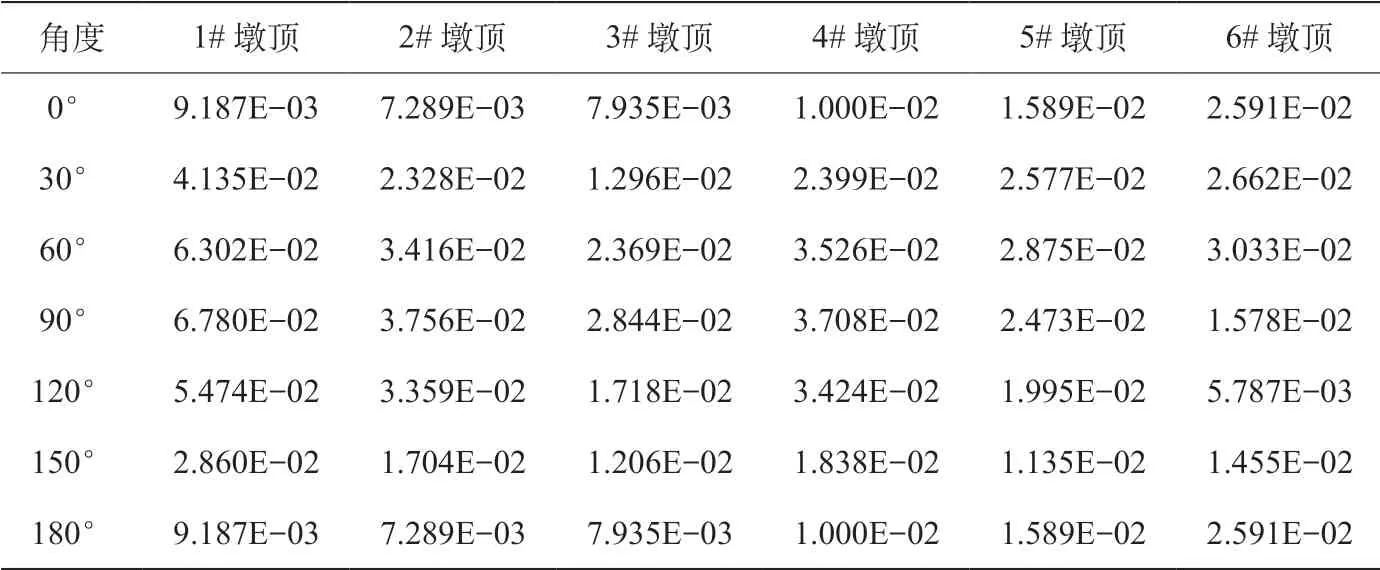
表2 墩頂y向位移 m

4.3 墩底 x 向彎矩分析

墩底x向彎矩如表3所示。由表可知，在地震動沿X向橋梁縱向輸入時，地震動輸入方向為0°時，1#、2#、3#、4#以及5#橋墩墩底彎矩值達到最大值，地震動輸入方向為30°時，6#橋墩墩底彎矩值達到最大值，而6#橋墩墩底在所有墩柱中彎矩值最大，最易發生彎曲破壞。 0°與180°正向及反向輸入墩底彎矩值一致。所有數據中，6#墩底彎矩值在30°地震動作用下明顯大于其他墩底彎矩值，因此，在實際施工過程中主要考慮地震動輸入方向30°時6#墩底彎矩即可。

表3 墩底x向彎矩 kN · m

4.4 墩底 y 向彎矩分析

墩底y向彎矩如表4所示。由表可知，在地震動沿Y向橋梁橫向輸入時，即地震動輸入方向為90°時，1#、2#、3#以及4#橋墩墩底彎矩值達到最大值，地震動輸入方向為60°時，5#橋墩墩底彎矩達到最大值，地震動輸入方向為30°時，6#橋墩墩底彎矩達到最大值，而1#橋墩墩底在所有橋墩中彎矩值最大，最易發生彎曲破壞。 0°與180°正向及反向輸入墩底彎矩值一致。所有數據中，1#墩底彎矩值在Y向地震動作用下明顯大于其他墩底彎矩值，因此，在實際施工過程中主要考慮地震動輸入方向90°時1#墩底彎矩即可。

表4 墩底y向彎矩 kN · m

4.5 梁跨中 x 向彎矩分析

梁跨中x向彎矩如表5所示。由表可知，在地震動沿Y向橋梁橫向輸入時，即地震動輸入方向為90°時，第一跨跨中彎矩達到最大值，地震動輸入方向為150°時，第二跨跨中彎矩達到最大值，地震動輸入方向為30°時，第三跨左跨中和右跨中彎矩分別達到最大值，而第三跨左跨中彎矩值大于所有梁跨中彎矩值，最易發生彎曲破壞。 0°與180°正向及反向輸入跨中彎矩值一致。所有數據中，第三跨左跨中彎矩值在30°地震動作用下明顯大于其他跨跨中彎矩值，因此，在實際施工過程中主要考慮地震動輸入方向30°時第三跨左跨中彎矩即可。

表5 梁跨中x向彎矩 kN · m

4.6 梁跨中 y 向彎矩分析

梁跨中y向彎矩如表6所示。由表可知，在地震動沿Y向橋梁橫向輸入時，即地震動輸入方向為90°時，第一跨跨中彎矩值達到最大值，地震動輸入方向為120°時，第二跨跨中彎矩值達到最大值，地震動輸入方向30°時，第三跨左跨中和右跨中彎矩值分別達到最大值，而第二跨跨中彎矩值在地震動輸入方向120°時大于所有梁跨中彎矩值，最易發生彎曲破壞。 0°與180°正向及反向輸入跨中彎矩值一致。第二跨跨中彎矩值在120°地震動作用下明顯大于其他跨跨中彎矩值，因此，在實際施工過程中主要考慮地震動輸入方向120°時第二跨跨中彎矩即可。

表6 梁跨中y向彎矩 kN · m

5 結論

本文以“人”字形曲線高架橋為研究對象，研究在不同方向地震動輸入下結構的相應特點，主要得出以下結論。

（1）曲線橋梁的直線段墩頂位移最大值明確沿著縱向或橫向發生，結構響應與地震動輸入方向有關聯；對于某些地震動輸入角度，曲線段墩頂位移最大值較直線段墩頂位移最大值小，表明地震發生時，曲線橋梁的直線段可能更易發生落梁現象。

（2）地震動輸入方向為 0°與180°時，位移與彎矩的響應結果一致。

（3）對于不同方向地震動輸入，墩底或跨中彎矩最大值響應規律不一。因此對于曲線高架橋，需進行多角度地震動輸入的抗震性研究，才能更全面的反映結構整體抗震性能。

（4）本文研究僅是在每間隔30°角度作用下進行最不利地震動研究，對于更復雜的橋梁抗震設計時需要具體分析，以便更全面的研究和體現橋梁抗震性能。