拓展視角 挖掘內涵 滲透數學文化
——“復數的三角表示”教學的幾點認識
?江蘇省太倉市明德高級中學 顧麗琴
1 引言
“復數的三角表示”是人教A版(2019年)高中數學必修第二冊的選學內容,主要包含復數的三角表示式和復數乘、除運算的三角表示及其幾何意義兩部分.這個內容是新教材的新增內容,且不列為考試命題的范圍,基于此許多教師認為不教也罷,或讓學生自學.但筆者以為,既然是教材內容,就都有教的必要.對此筆者談幾點認識,供大家參考.
2 為什么“復數的三角表示”不可“棄而不教”?
教材是教師組織日常教學的必備文本,離開教材的教學難免會偏離教學大綱的要求.如果每位教師都脫離教材,想怎么教就這么教,那么必然會導致教學的混亂.所以數學教學必須尊重教材,嚴格按照教材實施教學.或許有人會說,既然“復數的三角表示”高考不會考到,何必把時間浪費在不考的內容上,筆者以為這種想法十分膚淺.復數的代數表示法和三角表示法將中學數學中的許多知識點聯系在一起,用點、向量、三角來表示復數,不僅溝通了不同數學分支間的聯系,也體現了代數和幾何的有機結合.筆者認為“復數的三角表示”不可“棄而不教”,有以下三條理由.
2.1 現代教育理念的要求
教育是為了什么,這是一個永恒的話題.許多人認為高中教育就是讓學生考入大學,在這種思維的指揮下,教育變成了教學,教學又變成了應試教學,學校成了高考的“流水線”,于是出現了“為考而教”的怪相,把“一切為了學生”變成了“一切為了考試”.所以為了擺脫應試教育的束縛,體現為學生終身發展而教的教育理念,“復數的三角表示”不可“棄而不教”.
2.2 現行教學內容的要求
復數是數系擴充的“終結版”.復數必學內容主要包含復數的概念和復數的四則運算,其中內含復數的幾何意義和復數加減法的幾何意義,但這里沒有提及復數乘法與除法的幾何意義.為了解決這個問題,提倡并鼓勵學生學習“復數的三角表示”,否則對復數的認識就缺乏完整性,同時也體會不到復數運算與其他數學知識之間的內在聯系.此外,復數有著十分豐富的數學文化背景,如完美的棣莫佛定理([r(cosθ+i·sinθ)]n=rn(cosnθ+isinnθ)(n∈N*)),能引發學生的好奇,激發他們對數學的學習興趣.
2.3 提升數學素養的要求
數學教育的目標是為了提升學生的數學素養和數學綜合能力.數學是一個整體,數學知識之間存在著必然的聯系,而這種聯系不僅能幫助學生構建知識網絡,形成知識體系,而且能引導他們用不同的觀點與方法去分析問題和解決問題,從而不斷提升數學素養.復數可謂鏈接三角函數、平面向量及平面幾何的“局域網”,復數的三角表示是這張“局域網”的關鍵點,正是有了復數的三角表示,才能體現出復數的乘法與除法的幾何意義,并為復數的運算開辟了“廣闊的前景”.由此可見,復數的三角表示能體現出復數的價值,能幫助學生站在新的高度把握數學知識間的聯系,基于此,“復數的三角表示”不可“棄而不教”.
3 “復數的三角表示”該如何教?
既然“復數的三角表示”不可“棄而不教”,那么作為教師對這一內容該如何教?筆者以為應該抓好以下四點.
3.1 注重知識的關聯,恰當引入,讓學生理解復數的三角表示形式
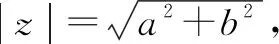
問題1:回顧三角函數的定義,如圖1,角θ的終邊上一點P(x,y),設P到原點O的距離|OP|=r,那么怎樣用角θ和r表示x,y?
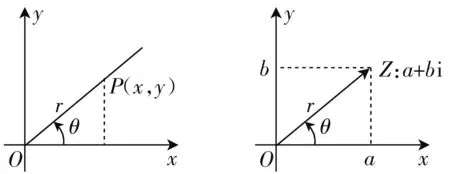
圖1 圖2
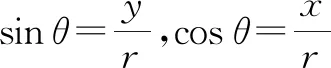
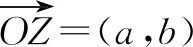
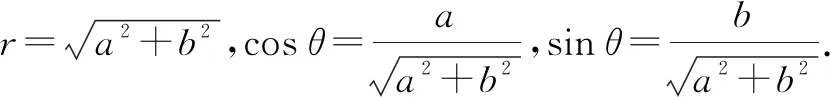
3.2 理解復數乘除法的幾何意義,讓學生感悟知識的內涵
兩個以代數形式給出的復數進行乘除后,其幾何意義不明顯,而將復數的代數形式轉化為三角形式后會是怎樣呢?教師可以通過代數運算和數形結合兩條途徑來引導學生探究.

問題4:能依據你的計算結果說出復數乘法與除法的幾何意義嗎?
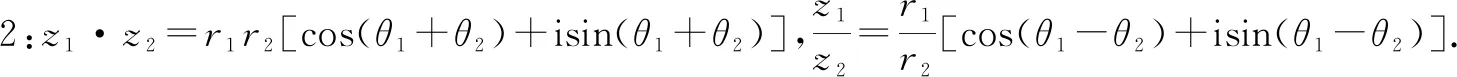
生3:兩個復數相乘,積的模等于各復數的模的積,積的輻角等于各復數的輻角的和;兩個復數相除,商的模等于被除數的模除以除數的模所得的商,商的輻角等于被除數的輻角減去除數的輻角所得的差.
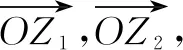
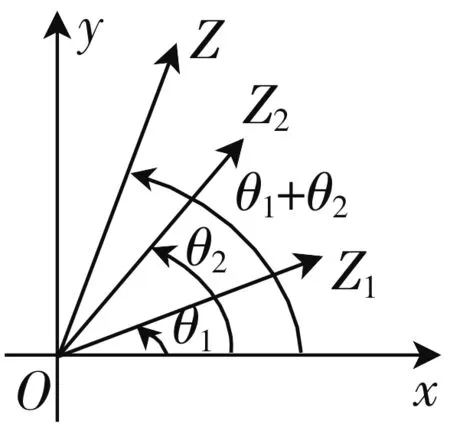
圖3
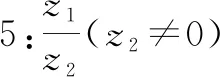
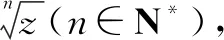
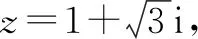
通過問題5,引導學生發現棣莫佛定理([r(cosθ+isinθ)]n=rn(cosnθ+isinnθ)(n∈N*),滲透數學文化.
3.3 拓展視角,體會復數三角形式的優越性
關于復數三角式的乘除運算的數學應用,筆者建議所選例題要體現用復數的三角形式解題的簡便性和優越性,如:

解析:利用復數乘法的幾何意義求得點C對應的復數.

故答案為:-2i
4 結語
復數內容在高中數學教材中占比較小,在高考的命題中占比也較小,但它作為數學中的一個獨立體系,依然有獨特的思想方法和教學價值,可謂“麻雀雖小五臟俱全”.從培養學生的核心素養角度看,對于教材中出現的任何復數內容,我們都不可等閑視之.以上觀點純屬筆者一孔之見,不當之處敬請指正.

