明考向 提素養
——基于2021年八省聯考數學試卷的分析與思考
?安徽省宣城中學 沈張軍
1 引言
隨著高中數學新課程標準的進一步推進與全面實施,高考數學命題越來越回歸本質,越來越注重對核心素養的考查.因此,只有全面聚焦數學核心素養的養成,才能從容應對高考的變化.
2 數學抽象
例1(2021年普通高等學校招生全國統一考試模擬演練(八省聯考)數學·15)寫出一個最小正周期為2的奇函數f(x)=______.
分析:滿足題目條件的函數是最小正周期為2的奇函數,合理聯想,數學抽象,可以考慮三角函數中的正弦型函數,再結合這兩個條件(最小正周期為2,奇函數)分別確定對應的參數值,即可確定滿足條件的一個函數解析式.
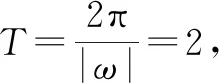
點評:數學抽象在高考數學命題中的具體表現主要體現在以下幾個方面:(1)形成數學概念與規則;(2)形成數學命題與模型;(3)形成數學方法與思想;(4)形成數學結構與體系.
3 直觀想象
例2(2021年普通高等學校招生全國統一考試模擬演練(八省聯考)數學·11)(多選題)圖1是一個正方體的平面展開圖,則在該正方體中( ).

圖1 圖2
A.AE∥CDB.CH∥BE
C.DG⊥BHD.BG⊥DE
分析:借助平面幾何圖形的折疊加以還原,由平面展開圖還原為正方體,結合直觀想象與空間想象,根據正方體的基本性質加以分析與處理.
解析:由正方體的平面展開圖還原正方體的直觀圖ABCD-EFGH,如圖2所示,由圖形可知AE⊥CD,故選項A錯誤;
由HE∥BC,HE=BC,可得四邊形BCHE為平行四邊形,所以CH∥BE,故選項B正確;
因為DG⊥HC,DG⊥BC,HC∩BC=C,所以DG⊥平面BHC,又BH?平面BHC,所以DG⊥BH,故選項C正確;
因為BG∥AH,而DE⊥AH,所以BG⊥DE,故選項D正確.
故選:BCD.
點評:直觀想象在高考數學命題中的具體表現主要體現在以下幾個方面:(1)利用圖形描述數學問題;(2)利用圖形理解數學問題;(3)利用圖形探索和解決數學問題;(4)構建數學問題的直觀模型.
4 邏輯推理
例3(2021年普通高等學校招生全國統一考試模擬演練(八省聯考)數學·3)關于x的方程x2+ax+b=0,有下列四個命題:
甲:x=1是該方程的根;乙:x=3是該方程的根;
丙:該方程兩根之和為2;丁:該方程兩根異號.
如果只有一個假命題,則該命題是( ).
A.甲 B.乙 C.丙 D.丁
分析:對于涉及方程的命題真假的判斷,破解的關鍵就是進行合理的邏輯推理.對甲、乙、丙、丁分別假設是假命題進行分類討論,結合已知條件求出方程的兩根,再結合各命題的真假進行判斷.
解析:若甲是假命題,則乙、丙、丁是真命題,則關于x的方程x2+ax+b=0的一根為3,由于兩根之和為2,則該方程的另一根為-1,兩根異號,合乎題意;
假若乙是假命題,則甲、丙、丁是真命題,則x=1是方程x2+ax+b=0的一根,由于兩根之和為2,則另一根也為1,兩根同號,不合乎題意;
假若丙是假命題,則甲、乙、丁是真命題,則關于x的方程x2+ax+b=0的兩根為1和3,兩根同號,不合乎題意;
假若丁是假命題,則甲、乙、丙是真命題,則關于x的方程x2+ax+b=0的兩根為1和3,兩根之和為4,不合乎題意.
綜上所述,甲命題為假命題.故選:A.
點評:邏輯推理在高考數學命題中的具體表現主要體現在以下幾個方面:(1)發現和提出命題;(2)掌握推理的基本形式和規則;(3)探索和表述論證的過程;(4)構建命題體系;(5)表達與交流.
5 數學運算
例4(2021年普通高等學校招生全國統一考試模擬演練(八省聯考)數學·17)已知各項都為正數的數列{an}滿足an+2=2an+1+3an.
(1)證明:數列{an+an+1}為等比數列;
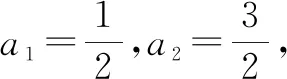
分析:第(1)問證明等比數列比較容易;而第(2)問求解數列的通項公式,可以合理借助第(1)問的結果,結合數列的遞推關系式的變形,從而破解相關問題.
解析:(1)由an+2=2an+1+3an,可得an+2+an+1=3an+1+3an=3(an+1+an).因為數列{an}的各項都為正數,則有a1+a2>0,所以數列{an+an+1}是以a1+a2為首項,公比為3的等比數列.
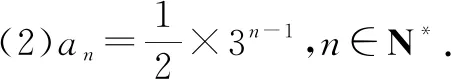
點評:數學運算在高考數學命題中的具體表現主要體現在以下幾個方面:(1)理解運算對象;(2)掌握運算法則;(3)探索運算思想;(4)設計運算程序.
6 數學建模
例5(2021年普通高等學校招生全國統一考試模擬演練(八省聯考)數學·6)(1+x)2+(1+x)3+……+(1+x)9的展開式中x2的系數是( ).
A.60 B.80 C.84 D.120
分析:利用等比數列加以數學建模,通過轉化法破解本題的關鍵是巧妙借助二項式展開式的通項公式規律,結合等比數列的定義以及求和公式進行求和處理,再結合和式的特征,通過確定相關二項展開式的系數來達到轉化的目的.
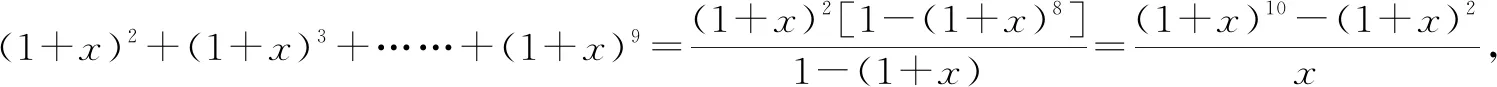
點評:數學建模在高考數學命題中的具體表現主要體現在以下幾個方面:(1)發現和提出問題;(2)建立模型;(3)求解模型;(4)檢驗結果和完善模型.
7 數據分析
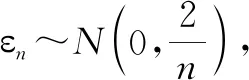
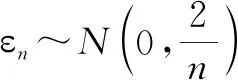
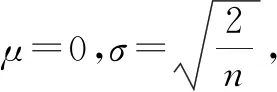
點評:數據分析在高考數學命題中的具體表現主要體現在以下幾個方面:(1)數據獲取;(2)數據分析;(3)知識構建.
8 結語
明確高考新動向,全面提升核心素養,這就要求我們在平時數學教學與數學學習過程中,切實融入數學核心素養的培育,重視閱讀能力的培養,學會思考,進行有效數學建模.在問題思考中進行有效數學抽象,充分主動獲取相關知識,進行合理邏輯推理,提高邏輯推理與論證能力,親身體驗數學的發展歷程與變化規律.通過直觀想象、數學運算或數據分析等方式,有效理解和掌握相關知識.真正有利于學生的各方面發展,充分培養核心素養,提升能力.

