多維度研究三角形內部長度問題

?四川省鄰水中學 林冰雁

1 問題呈現

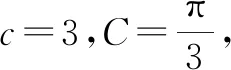
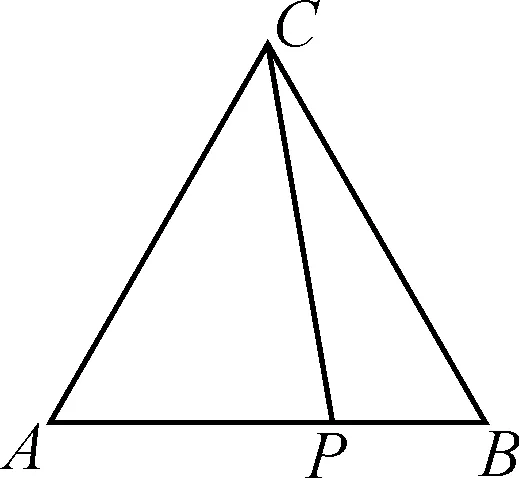
圖1

2 問題分析

此題以銳角三角形為背景，已知一角C及其對邊AB，和對邊上一點P，求三角形內部線段CP所在邊的最大值.選取正確的角度作為解題的切入點是關鍵的一步.根據題目所給的信息，從已知出發，利用“正弦定理與余弦定理[1]”進行簡單計算，而長度的最值問題容易涉及到“三角函數和向量[2]”、函數與方程等知識，其中的變形與推理精彩絕倫.還可利用直線的參數方程中t的幾何意義輕松解決該問題.最后巧妙結合“圓[3]”的性質并進一步建立平面直角坐標系，將坐標法與三角函數相結合，實現知識的貫穿性.

3 解法探究

3.1 思維視角一：邊化角思維

解法1：在△BCP中，由余弦定理可得

CP2=a2+1-2acosB.

(顯然，|CP|跟a和角B都有關系，但是無法直接求得最大值，進一步思考邊a能否化成角B呢？)

在△ABC中，利用正弦定理可知

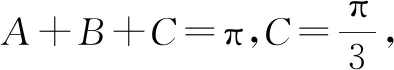
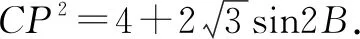
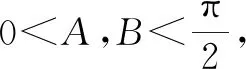
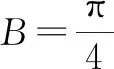
點評：解法1比較典型，其主要思路是先利用余弦定理將CP2表示出來，以正弦定理作為橋梁，將邊a轉化成同一個角B，進一步結合題意確定該角的范圍，接著利用三角恒等變換將CP2轉化為三角函數模型，最后借助三角函數的性質求得最大值.

那還有其他的方法嗎？線段的長度即向量的模，解三角形通常與向量的知識相聯系.向量法是指根據題意選擇合適的基底，將所求線段用向量表示出來，利用平面向量基本定理和運算法則解題，將幾何問題轉化為向量運算問題，轉換了解題的方向.

3.2 思維視角二：向量思維

解法2：如圖2，過點P作BC的平行線交直線AC于點M，過點P作AC的平行線交直線BC于點N.

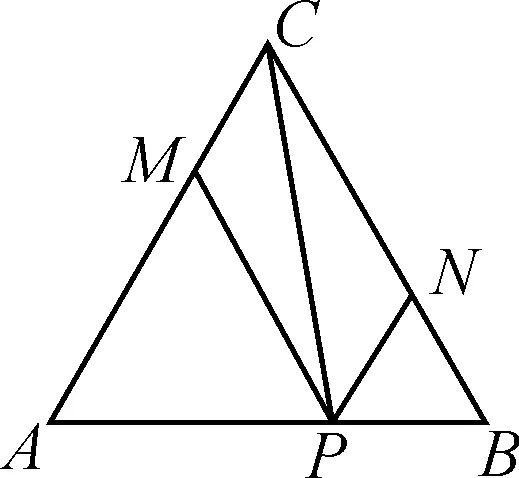
圖2

由相似三角形的判定方法知△APM∽△ABC，△BPN∽△BAC.

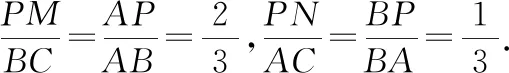
又四邊形PMCN是平行四邊形，則

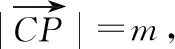
9m2=b2+4a2+2ab.

①

在△ABC中，由余弦定理可得

9=b2+a2-ab.

②

由式①②消去ab,得9m2=3(2a2+b2-6).

也就是說，要求m的最大值，只需求2a2+b2的最大值.

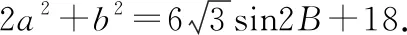
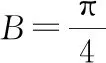
點評：根據題意，利用三角形相似，尋找相關線段的相似比，結合平面向量基本定理和線性運算，借助余弦定理的應用，找出CP2與a，b間的關系，最后利用邊化角思維求得最大值.

以上2種方法從代數角度著手，那能不能從形的角度思考呢？由于角C和對邊AB給定，因此考慮在圓上固定AB，再把角C看作劣弧AB所對的圓周角構造△ABC.

3.3 思維視角三：幾何思維

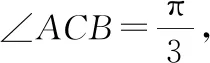
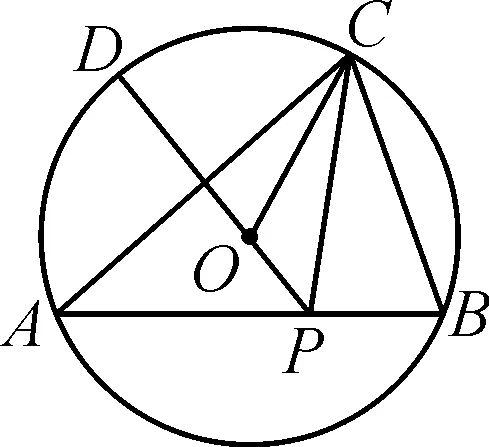
圖3

顯然，當點C運動到點D時有最大值，即|CP|max=|DP|.

如圖4，連接AO，BO，過點O作AB的垂線交AB于點H，則∠AOB=120°.

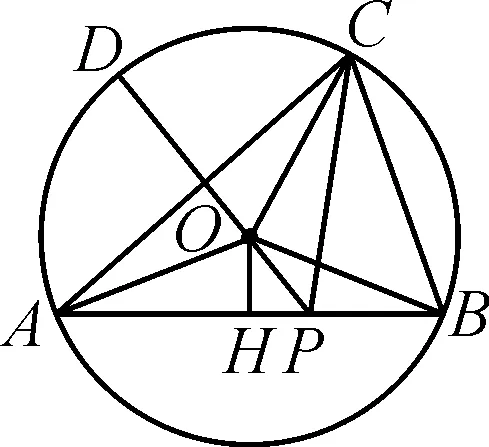
圖4

在△AOB中，由余弦定理可得

c2=AO2+BO2-2AO·BO·cos∠AOB.

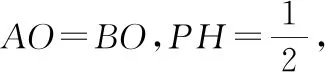
點評：有效借助工具“圓”，將代數問題轉化為幾何問題，巧妙利用圓的性質找到|CP|的最大值——|DP|，利用數形結合與余弦定理算出最大值.

3.4 思維視角四：坐標系思維

在解法3的基礎上，如果建立平面直角坐標系，則可以利用兩點的坐標研究該線段的長度.

(1)坐標法.

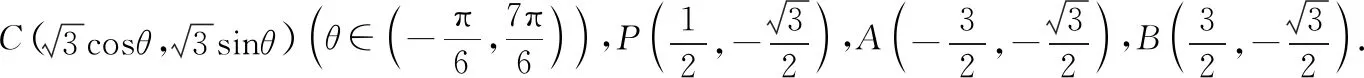
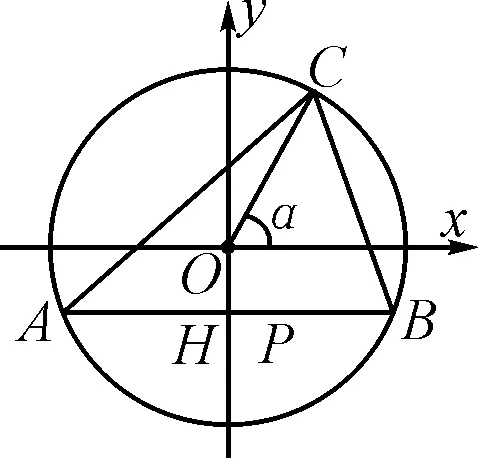
圖5

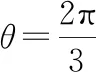
點評：在引入圓的知識并建立平面直角坐標系后，根據圓的幾何性質以及三角函數的定義尋找目標點的坐標，本質上利用了點C的軌跡是圓的一部分(優弧AB)，使問題得以簡化，結合兩點間的距離公式直接給出CP2，將其表示成三角函數模型，求出最大值.

(2)參數方程法.

解法5：如圖6，建立平面直角坐標系xOy，連接CP交圓O于點D.設α(α∈(0,π))是直線CP的傾斜角.

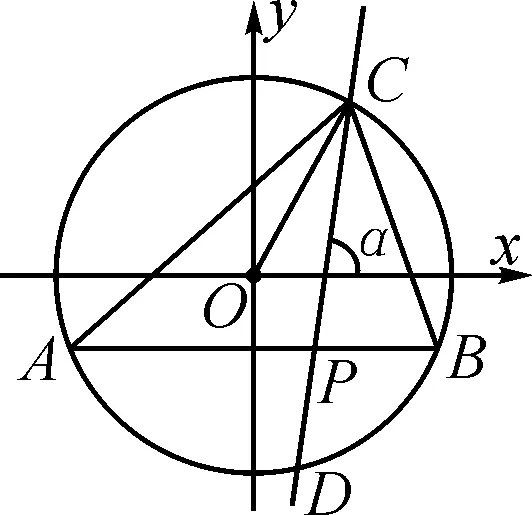
圖6

因此圓的標準方程為x2+y2=3，直線CP的參數方程為

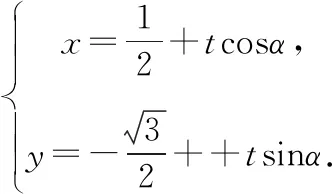
聯立直線的參數方程和圓的標準方程，整理得到

顯然Δ>0，設點C，D對應的參數分別為t1，t2.由圖6知t1>0，t2<0，因此有

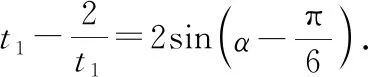
點評：以點P為定點，設出直線CP的標準參數方程，聯立該方程和圓的方程得到關于t的一元二次方程，利用參數t的幾何意義得到CP的最大值即點C所對應參數的絕對值的最大值，從而轉化為求函數的最大值，最后結合三角函數的性質求出CP的最大值.

4 結論

在解三角形問題中，涉及的知識點多，覆蓋面廣，本文中主要從4個不同的思維視角解決已知兩個元素的三角形內部邊長的問題.

(1)邊化角思維：尋找三角形中成立的關系式，分析其特征，通過正弦定理將邊轉換為角，進而利用三角函數的思想求解最大值.

(2)向量思維：利用平面向量基本定理將目標線段所在向量線性表示，通過余弦定理發現兩個重要的式子①②，借助邊化角思維進行轉換，結合三角函數的性質分析出最大值.

(3)幾何思維：構造三角形的外接圓，利用圓的性質和幾何特征解題，強調數形結合思想，直觀形象地求出最大值.

(4)坐標系思維：通過建立平面直角坐標系，不僅可以利用兩點間的距離公式和三角函數知識分析最大值，還巧妙結合直線標準參數方程中參數的幾何意義，運用韋達定理和函數的單調性求得最大值.