新穎背景設置 創新意識應用
?甘肅省民樂縣第一中學 展斌國
1 引言
創新類問題是歷年高考數學試卷中的一道亮麗風景線,幾乎每年高考試卷中都能見到她們的“倩影”.此類新穎問題在原有數學基礎上結合定義、性質、公式、方法等視角加以創新,通過綜合與類比等思維的應用,巧妙把相關的數學知識、數學思想方法與數學能力等加以合理融合,達到創新能力與創新應用的統一,數學知識與數學能力的綜合,真正達到創新應用的目的.
2 定義創新
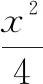
分析:結合創新定義,利用待定系數法來分析與處理.通過改變相應的二次曲線方程以及已知點的情況,抓住關系,引入系數,利用方程的轉化,結合方程的判別式,通過解答二次不等式的方式來破解取值范圍,從而確定相應的最值.
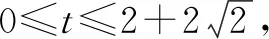
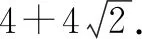
點評:破解此類創新定義類問題時,關鍵是抓住題目中的定義,結合新規則的信息遷移,以及考生的閱讀理解、獲取信息、處理信息等能力,充分挖掘新定義的實質,尋找新規則的內涵,找出新規則的特點,依規則便可快速解題.
3 性質創新
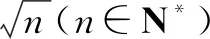
分析:結合創新性質,設出對應的函數關系式并建立相應的不等式,借助合理的運算與數論知識來分析,進而確定對應的參數值.
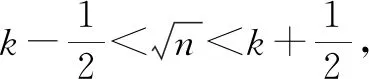
故填答案:332.
點評:破解此類創新性質類問題時,關鍵是建立創新性質所對應的函數關系式、不等關系式等,尋找問題破解的切入點,有效融合創新意識與應用意識,合理破解相應的創新問題.
4 公式創新
例3“無字證明”是數學的一大創新應用,其是將數學命題(公理、公式等)用簡單、有創意而且易于理解的幾何圖形直觀呈現出來.請根據給出的平面幾何圖形寫出該圖(如圖1)所驗證的一個三角恒等變換公式:______.
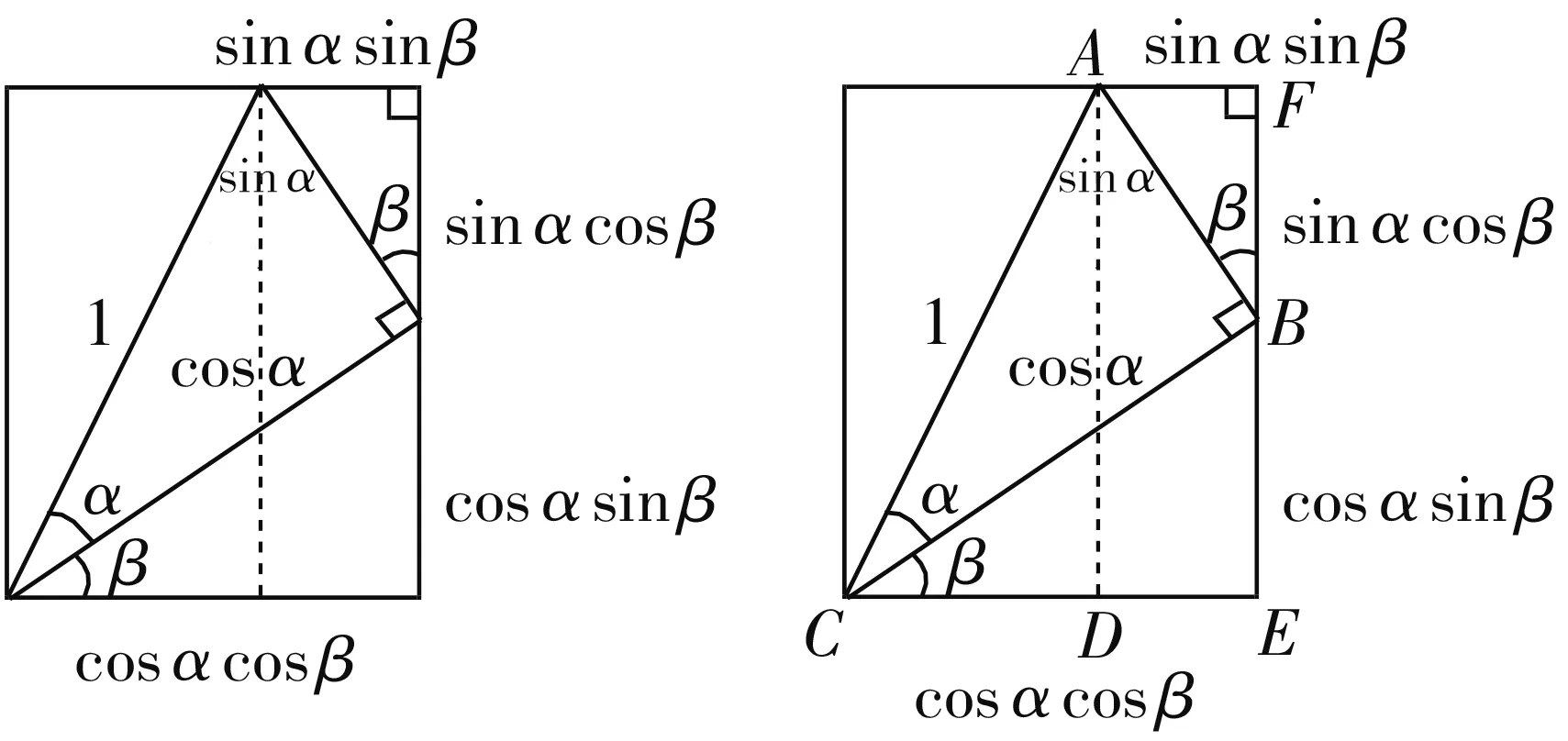
圖1 圖2
分析:借助“無字證明”的創新設置,通過幾何圖形的呈現加以直觀分析,結合幾何圖形中線段的關系與三角函數的關系加以抽象與驗證,提升對公式的理解與記憶.
解析:如圖2所示,令AC=1,∠ACB=α,∠BCE=β,則在Rt△ABC中,可得BC=cosα,AB=sinα.
在Rt△BCE中,BC=cosα,∠BCE=β,可得CE=cosαcosβ,EB=cosαsinβ;
在Rt△AFB中,AB=sinα,∠ABF=β,可得BF= sinαcosβ,AF=sinαsinβ.
則CD=CE-DE=CE-AF=cosαcosβ-sinα·sinβ,AD=EF=BF+EB=sinαcosβ+cosαsinβ.
而在Rt△ADC中,CD=cos(α+β)·AC=cos(α+β),故cos(α+β)=cosαcosβ-sinαsinβ;
AD=sin(α+β)·AC=sin(α+β),故sin(α+β)=sinαcosβ+cosαsinβ.
故答案為:cos(α+β)=cosαcosβ-sinαsinβ或sin(α+β)=sinαcosβ+cosαsinβ.(答案不唯一)
點評:破解此類創新公式類問題時,關鍵是借助平面幾何圖形中線段的長度關系,結合直角三角形的三角函數定義加以合理推理論證.合理借助“無字證明”的創新設置,把三角恒等變換公式的推導直觀化,方便理解與記憶,把公式、圖形、應用等有機融合,考查知識與能力的同時,考查直觀想象、邏輯推理等核心素養.
5 方法創新
例4根據下面公式的推導過程:
sin 3θ=sin(2θ+θ)=sin 2θcosθ+cos 2θsinθ=2sinθcos2θ+(1-2sin2θ)sinθ=2sinθ(1-sin2θ)+(sinθ-2sin3θ)=3sinθ-4sin3θ.
解答下列問題:
(1)證明:cos 3θ=4cos3θ-3cosθ;
分析:通過題目條件中公式的推導過程,類比對應的證明方法來推導三倍角余弦公式;并利用公式的應用合理化簡函數f(x)的解析式,尋找函數f(x)有零點的充要條件,進而確定實數m的取值范圍.
解析:(1)cos 3θ=cos(2θ+θ)=cos 2θcosθ- sin 2θsinθ=(2cos2θ-1)cosθ-2sin2θcosθ=2cos3θ-cosθ-2(1-cos2θ)cosθ=4cos3θ-3cosθ,即cos 3θ=4cos3θ-3cosθ;
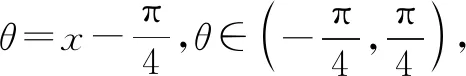
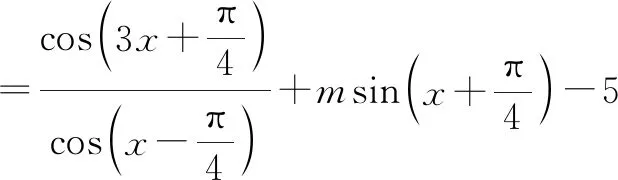
=3-4cos2θ+mcosθ-5
=-4cos2θ+mcosθ-2.
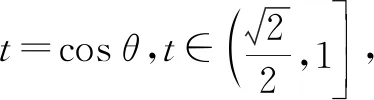
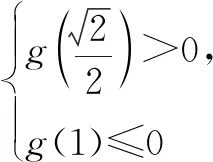

點評:破解此類創新方法類問題時,關鍵是通過閱讀相關的方法加以合理類比與應用,知識的拓展等來綜合處理.
6 結論
創新類問題經常借助定義、性質、公式、方法等方面的創新與應用,結合約定的規則與要求,綜合數學知識、數學思想方法等加以合理融合,借助合理的推理論證、數學運算等加以分析與處理,有效達到綜合考查數學知識、數學思想方法和數學能力,以及解決數學問題的目的.具有較好的高考選拔性,很能體現考生的創新意識與創新應用.

