巧借向量共線定理 妙解數學應用問題
?安徽省阜陽市紅旗中學 常 麗
1 引言
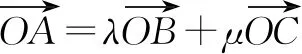
2 線性表示
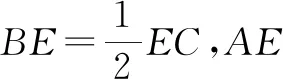
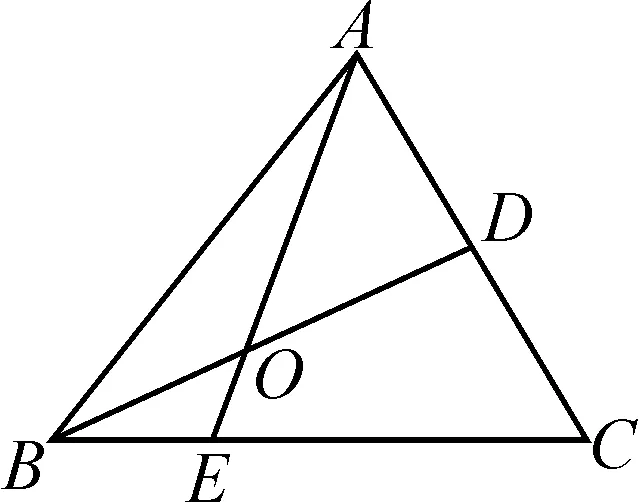
圖1

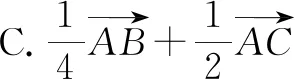
分析:根據三角形邊上的點所處的位置關系,引入參數來表示相應平面向量的線性關系,結合平面向量的線性關系與運算加以轉化,利用平面向量共線定理確定對應系數的關系式,進而得以確定參數值,為進一步確定平面向量的線性表示提供條件.
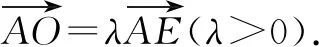
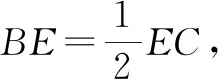
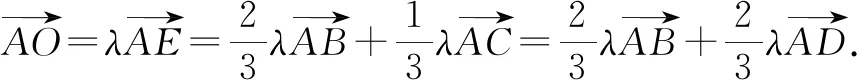
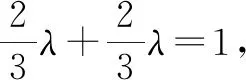
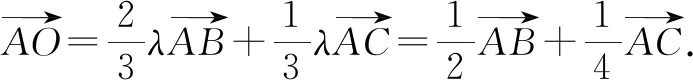
故選擇答案:A.
點評:涉及平面向量的線性表示問題,關鍵是通過平面向量的線性關系與運算加以合理化歸與轉化,這其中經常會利用平面向量的中點公式、平面向量共線定理等相關知識,合理構建從條件到結論之間的關系,實現平面向量的線性表示的轉化與應用.
3 參數求值
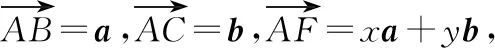
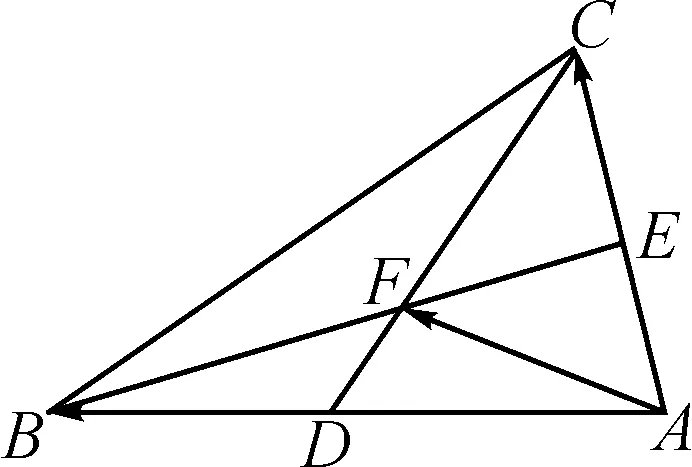
圖2
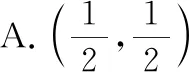
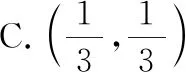
分析:利用條件中的平面向量的線性表示關系式,從不同角度與方向轉化相應的線性關系式,利用平面向量共線定理分別確定對應的系數關系式,結合方程組的求解來確定對應的參數值.具體破解時,通過構建“兩條線段的交點”的條件,借助轉化成兩次向量共線,進而確定交點位置.
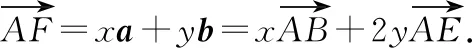
由于B,F,E三點共線,利用平面向量共線定理可得x+2y=1.
①
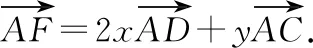
由于D,F,C三點共線,利用平面向量共線定理可得2x+y=1.
②
點評:涉及平面向量的參數求值問題,往往通過題目條件中的平面向量的線性關系式進行合理變形與轉化,實現滿足平面向量共線定理的條件,進而利用平面向量共線定理構建系數之間的關系式,從而得以確定對應的參數求值問題.
4 線段比例
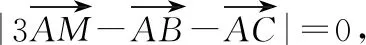
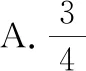
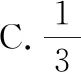
分析:根據題目條件轉化為平面向量的線性關系式,引入線段的中點,利用平面向量的中點公式加以轉化,構建向量之間的線性關系,利用平面向量共線定理確定對應線段的比例關系,進一步利用三角形之間面積的關系,合理確定相應的比值,從而得到對應三角形面積的比值問題.
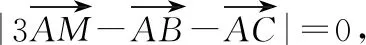
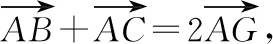
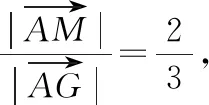
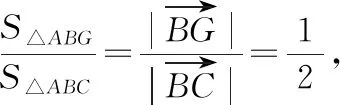
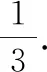
故選擇答案:C.
點評:涉及平面向量的線段比例問題,破解的關鍵就是合理挖掘題目條件,利用平面向量共線定理,構建不同平面向量之間的線性關系,結合系數的正負取值情況確定相應線段之間的比例關系.此類問題的表示形式可以是線段比例關系的確定、三角形面積的比值、位置關系的判定等相關的應用問題.
5 求數量積
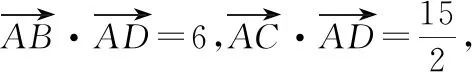
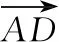
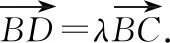
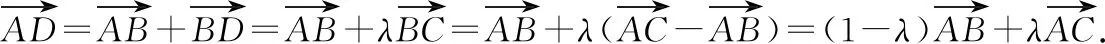
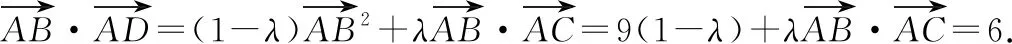
③
④
點評:涉及平面向量的求數量積問題,破解的關鍵是結合平面向量共線定理構建相應向量之間的線性關系,結合平面向量的數量積公式加以展開與轉化,可以用來解決平面向量的數量積的求值、模的確定、系數的求解等相關問題.
6 綜合應用
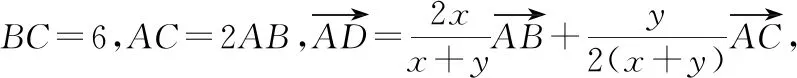
分析:通過平面幾何圖形中輔助線的構建,結合平面向量的線性關系式的變形與轉化,結合系數之間的關系式,利用平面向量共線定理確定三點共線,從而確定對應函數的最小值的取值情況,結合余弦定理以及同角三角函數基本關系式,利用三角形面積公式的轉化,結合二次函數的圖象與性質來確定相應的最值問題.
解析:如圖3所示,取線段AC的中點N,延長AB至點M,使得AB=BM.
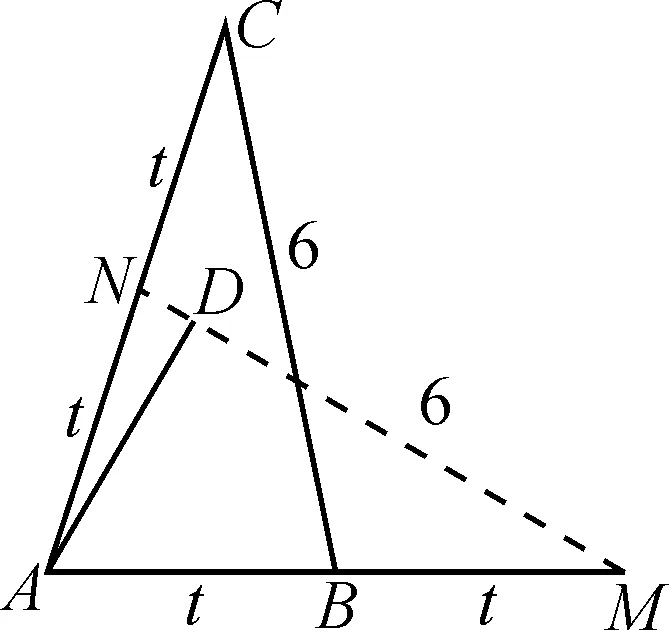
圖3
設AN=t>0,則AC=2t,AB=BM=t.
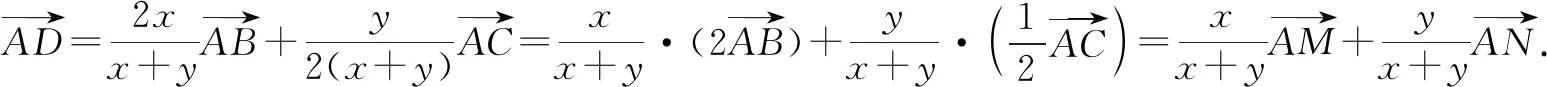
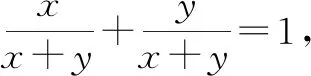
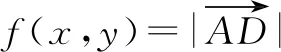
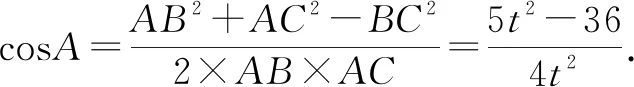
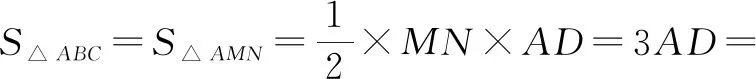
所以f(x0,y0)的最大值為4.故填答案:4.
點評:涉及平面向量的綜合應用問題,往往綜合平面向量、函數與方程、不等式、三角函數、平面幾何與平面解析幾何等相關的問題,結合題目條件,合理利用平面向量共線定理加以轉化與應用,以及對應的相關知識來綜合分析與應用,從而得以破解相應的綜合應用問題.
7 結束語
作為平面向量中最基本的定理之一的平面向量共線定理,可以合理有效地構建起不同向量之間的線性關系以及不同點之間的位置關系.具體應用時主要涉及幾個方面:一是正用,即利用定理證明向量共線(或三點共線、線線平行)等;二是逆用,即已知兩個向量共線,那么其中一個向量必然可用另一個向量線性表示;三是綜合應用,即利用向量的工具性來解決一些綜合性應用問題.

