“類比教學”在高中數學中的運用
——以“函數的零點與方程的解”為例
?哈爾濱師范大學教師教育學院 譚 娜
1 類比教學在高中數學教學中的運用
類比教學是一種很重要的教學手段,是教師在教學中引導學生采用類比的方法找到知識間的相互聯系進而分析問題、解決問題的一種教學[1],能幫助學生在新舊知識間搭建橋梁[2].在類比教學中,教師要善于抓住新舊知識的聯系,找到合適的類比形式.常見的類比教學法的分類有形式類比、過程類比以及思想類比[3].在教學過程中,教師要根據具體的知識內容,選擇不同的類比形式.但無論是哪一種類比形式,在類比教學中都要引導學生發現知識之間的聯系,探索新知識的生成過程,從舊的知識規律中發現新的知識規律.
類比教學在各個學科都有廣泛應用,特別是在數理科學教學中,它是一種常見且十分重要的教學策略.眾多學者在課堂實踐中發現類比教學不但有利于學生對知識的吸收,還有助于培養學生的科學思維能力.康穎教授將類比法運用于物理教學中發現,類比教學不但能提高教學效果,更重要的是能讓學生掌握類比聯想的思維方法[4].
數學具有很強的抽象性和邏輯性,知識與知識之間有許多的聯系,類比是發現概念、公式和定理的重要手段.教師在教學中要注重類比思維的滲透和運用,引導學生思考新知識與過去學過的哪些知識相似,找到新舊知識聯系的橋梁,借用舊知識中的規律來分析新知識中是否存在相應的規律.在情境引入時,創設類比情境,引導學生在熟悉的知識中發現新知識的情境[5],此外,在知識生成、解題訓練等環節中都可以運用類比教學提高課堂效率.
2 “函數的零點與方程的解”教學設計
2.1 類比教學的運用
本節內容舊教材在探究中提出:“一元二次方程ax2+bx+c=0(a≠0)的根與二次函數y=ax2+bx+c=0(a≠0)的圖象有什么關系?”通過探究活動,由特殊到一般,引出零點的概念,并得出一般函數的零點、函數圖象與x軸的交點的橫坐標及其對應方程的根三者之間的關系.新教材在預備知識中學習的“一元二次方程的實數根就是相應二次函數的零點”為函數的零點與方程的解的學習奠定了知識基礎,以“能否用相應的函數來求解lnx+2x-6=0這種不能用公式求解的方程?”引入課堂.可以發現,新舊教材雖然在知識的編排順序上有所變化,但是新知識(函數零點及零點定理)都是在舊知識(方程的根、二次函數圖象與x軸的交點關系)的基礎上進行類比、探究和延伸.
因此,在“函數的零點與方程的解”的教學中,教師可以類比二次函數的零點及其零點存在的特點來學習本節知識,在二次方程及其相應的二次函數關系的基礎上建立一般函數零點的概念,進一步探究零點存在定理及其應用,將類比方法和轉化思想運用于教學中,培養和發展學生的類比思維能力,達到事半功倍的效果.具體類比見表1.
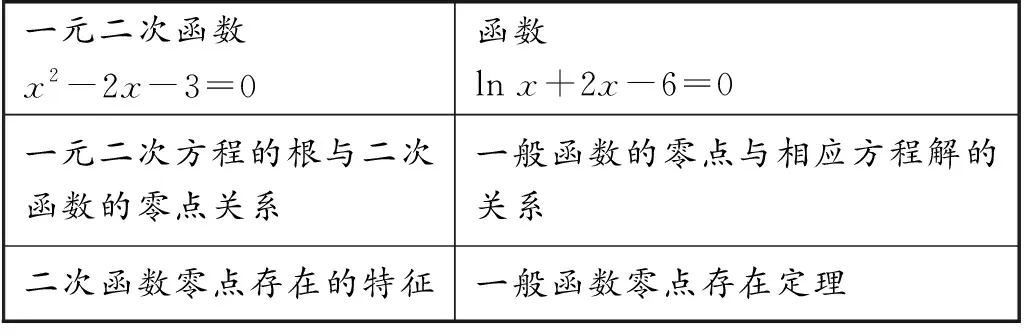
表1 “函數零點與方程的解”的類比表
2.2 教學過程


圖1 “函數的零點與方程的解”教學思維導圖
2.2.1 設置懸念,問題引入
在預備知識里我們學習了用二次函數的觀點來認識一元二次方程,知道一元二次方程的實數根就是相應二次函數的零點.你能求解方程 lnx+2x-6=0嗎?能否采用類似的方法,用相應的函數來研究它的解的情況呢?
設計意圖:由熟悉的知識出發,創設類比情境,激發學生的好奇心,引導學生從函數與方程的角度出發,建立函數與方程之間的關系.
2.2.2 類比探究,問題引導
問題1求方程x2-2x-3=0的實數根并畫出其對應的函數圖象,思考:該方程的根與相應函數的圖象有什么聯系?
思考1你能類比二次函數的零點得出一般函數的零點概念嗎?
思考2函數的零點是點嗎?
設計意圖:通過方程x2-2x-3=0和函數f(x)=x2-2x-3進一步理解方程、函數、圖象三者之間的關系,有利于學生對知識的吸收和掌握,喚起舊知,引發新的思考.從特殊到一般,類比抽象出函數的零點概念,并建立方程、函數、圖象三者之間的關系,進一步深入理解函數零點的概念并強調易錯點.
問題2下列方程是否有解,并進一步說明其相應函數的零點是什么?
(1)2x-3=0; (2)x2-2x-3=0;
(3)x2-2x+2=0; (4)lnx+2x-6=0.
追問:函數的零點在什么條件下存在呢?
設計意圖:趁熱打鐵,通過求解方程來求函數零點,加深學生對方程的解及其函數零點之間關系的理解.對于第(4)小題雖然無法求解但可以從函數圖象去猜零點,為后面函數零點存在定理的探究做好鋪墊.
問題3觀察函數f(x)=x2-2x-3的零點所在區間,此時函數圖象與x軸有什么關系?如何用函數f(x)的取值規律來刻畫這種關系呢?(提示:考慮f(a)·f(b)的正負.)
思考3如果函數f(x)在區間[a,b]上滿足f(a)·f(b)<0,那么該函數在此區間上一定有零點嗎?
設計意圖:觀察二次函數存在零點時函數圖象的特征,引導學生觀察零點附近函數值的特點,體會存在零點時函數圖象“穿過”x軸.學生合作交流找到零點及其所在區間,探究零點附近函數值的特點,通過二次函數零點存在時的區間端點函數值的特征類比歸納一般函數零點存在定理.
2.2.3 定理辨析,知識運用
問題4如果函數y=f(x)的圖象在區間[a,b]上是連續不斷的,且在區間 (a,b) 內有零點,那么是否一定有f(a)f(b)<0?
問題5什么情況下函數有唯一一個零點?
設計意圖:發散學生的思維,進一步深入理解函數零點存在的條件,說明定理的條件充分而不必要,培養學生的邏輯思維能力.為進一步推廣零點存在定理,強調零點存在定理只能判斷函數有零點,但不能說明有幾個零點;存在唯一零點時,函數必須在區間上單調.在不斷地追問和問題串的設置中讓學生深入理解零點存在定理滿足的條件以及零點存在定理的推論.
問題6你能求解方程lnx+2x-6=0嗎?如果有解,有幾個呢?
思考4你能判斷函數f(x)=lnx+2x-6 的零點個數嗎?你能證明函數f(x)=lnx+2x-6 是增函數嗎?
思考5由零點存在定理能說明函數有幾個零點嗎?
設計意圖:從開頭提出問題到最后解決問題,進一步加深學生對知識的理解和運用,提升學生的數學辨證能力;問題驅動學生的思考,歸納零點存在定理只能判斷函數是否有零點,但不能確定零點個數;通過師生共同探究加深學生對定理的理解,在定理探究的過程中提升學生數學抽象和邏輯推理的能力.
2.2.4 反思總結
(1)思考與總結:求解一個方程有哪些方法?什么條件下適合用零點存在定理?本節課中,我們是如何從一元二次函數零點以及零點存在知識類比推廣得出一般函數的零點及其零點存在定理的?總結見圖2.

圖2 “函數的零點與方程的解”類比教學圖
(2)課后思考:如果函數f(x)=lnx+2x-6在區間(2,3)內存在一個零點,你能將這個零點的范圍盡量縮小嗎?
設計意圖:回顧本節課知識形成的過程,體會類比思維在數學課堂的應用,加深學生對函數零點與零點存在定理的理解和運用.在課堂最后提出思考題,為后續學習埋下伏筆,使整個學習過程,形成一個有機的整體,為“二分法求方程的近似解”作鋪墊.
3 教學反思
在“函數的零點與方程的解”中采用類比教學,將二次函數的零點與方程的解和函數的零點與方程的解之間相結合,運用類比思維,借助問題串的引導,將新舊知識銜接,找到二者之間的聯系.引導學生學會應用類比思維學習新知識,將性質、形式等相近的問題聯系起來,轉化思路,這樣便能靈活地解決問題.特別是在零點定理的探究時,以二次函數為切入點,類比舊知識的規律,得到新知識的規律.
類比思維是一種重要的邏輯思維方式,只有深入研讀教材,充分理解教材,才能真正做好育人的工作.類比教學不僅能激發學生的學習興趣,加強學生對知識的理解,啟發學生的思維[6],還能培養學生的猜想能力、遷移推理能力以及創新性思維能力[7].在數學課堂上,教師需要善于引導學生發現新舊知識之間的聯系,培養學生的數學學習能力.

