厚植“三個理解” 篤行核心素養*
——以“平面向量數量積的坐標表示”教學為例

?浙江省寧波市咸祥中學 於家海

1 引言

辛丑孟春三月，市教研室專家馮斌一行來我校指導教學工作，學校安排筆者執教調研課“平面向量基本定理及坐標表示”.本節課良好的教學效果給專家、教師留下了較為深刻的印象，現將這節課的課堂實錄與教學感悟整理成文，與同行共饗.

2 教學過程簡錄

2.1 復習回顧，推陳出新

師：同學們，我們先回顧一下上節課的內容，請大家完成表格(表1).

表1 平面向量及其運算的坐標表示

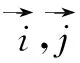
生1：兩類四種，分別是加法、減法、數乘三種線性運算和數量積運算.

師：向量的加法、減法、數乘都有了坐標表示，很自然地要問，數量積有嗎？

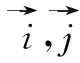
2.2 示范引領，探究發現

師：平面向量的數量積能否用坐標表示？

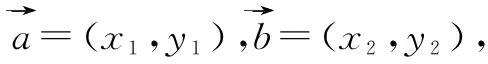
問題2我們給出的結果是符號語言，你能用文字語言表述此結論嗎？

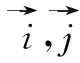
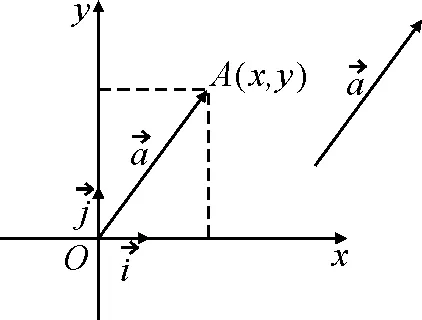
圖1

2.3 問題驅動，交流討論

師：我們已經得到平面向量數量積的坐標表示，請同學們先獨立思考，然后分小組討論，完成以下4個問題后再交流結果.

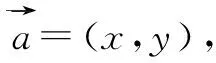
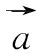
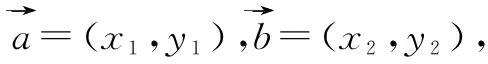
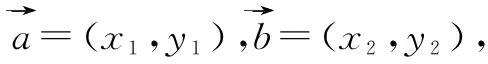
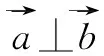
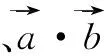
設計意圖:學生學習知識、掌握技能以及獲取信息固然重要，但更重要的是要“學會思考”“學會學習”，懂得如何掌握與運用知識、技能和信息，在“學會”中達到“會學”.因此，教師在課堂教學中要為學生搭設合理的平臺和“腳手架”，指導學生攀爬探索，從而真正成為為學生開啟知識大門的引路人.數學教學過程是數學活動的過程，也是數學思維活動的過程.讓學生“動起來”是產生數學思維活動的關鍵，而學生活動的驅動力就來源于問題.此環節中筆者采用問題串的形式展開教學，圍繞著平面向量數量積的坐標表示設計了4個具有一定思維價值的問題組成問題串，以問題為載體呈現并作為任務驅動，學生在分析問題、探究問題和解決問題的過程中發現、吸收、應用數量積的坐標表示新知識，使教學變“告訴”為“探索”，實現數學知識的“自然生成”.

2.4 深入探索，實踐應用

；

.

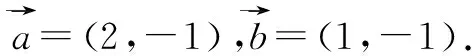
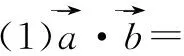
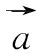
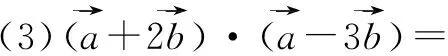
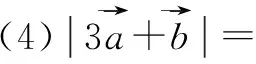
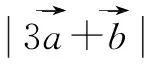
例2若點A(1,2)，B(2,3)，C(-2,5)，則△ABC是什么形狀？證明你的猜想.

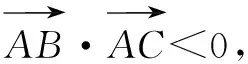
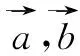
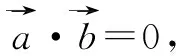
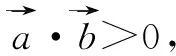
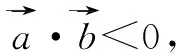
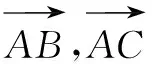
2.5 文理交融，提升小結

師：請同學們完成下列表格(表2).

表2 平面向量數量積以及向量垂直、平行的坐標表示

師：我們驚奇地發現借助向量坐標，既可以解決向量的加減、數乘、數量積運算問題，也能夠表示向量共線、垂直及夾角等問題，向量坐標真是“威力無窮”.為此老師模仿唐朝詩人白居易寫了一首《憶坐標》：

坐標好，用處真不少.加減乘積皆好用，共線模角俱應手.能不憶坐標？

設計意圖:特級教師文衛星老師說過，上一節自己滿意的課，需要把握好“三個度”即“知識適度，思想高度，文化厚度”.教師傳授給學生的不僅是“知”，更重要的是“識”.下課前的小結用精練、優美的語言把本節課的教學內容、方法等提升了思想高度，發展學生對向量坐標表示的整合、詮釋的能力，也體現了數學的文化價值，既能緩解緊張、沉悶的課堂氣氛，讓學生在輕松愉悅的環境下學習，還可以幫助學生理解、記憶所學數學知識，潛移默化、潤物無聲中提高了學生的思想境界和文化修養，陶冶學生情操，達到以知促情，知情結合的目的.

3 教學反思感悟

3.1 優化教學設計必須厚植“三個理解”

人教社章建躍先生提出“三個理解”，即理解數學，理解學生，理解教學.理解數學就是要把握數學內容的本質，特別是對教學內容所蘊含的數學思想和方法要有深入理解.向量是近代數學中最重要的概念之一，兼具幾何形式和代數形式的“雙重身份”，并且擁有一套優良的運算系統，即坐標表示，成為溝通代數與幾何的“重要工具”和“橋梁”.平面向量數量積的坐標表示就是運用坐標這一量化工具表達向量的數量積運算，為研究平面中的距離、垂直、角度等問題提供了全新的手段.理解學生就是要全面了解學生數學學習的思維規律，把握學生的認知特點、知識基礎、學習方式和習慣.在本節課中，針對新授向量數量積的坐標表示內容與學生已有加減、數乘的坐標表示等舊知數學經驗的聯系，設置復習導入環節，又根據當前知識(平面向量數量積的坐標表示)與學生已有認知結構的距離，在學生的思維“最近發展區”內設置問題1～7，從而激發學生求知欲、激活學生思維，使學生的心理保持積極的、適度的求知傾向，還聚焦學生向量書寫細節問題，對易錯、易混和疑惑點專門進行強調和分析，有的放矢地進行教學.理解教學就是要把握教學的基本規律，按教學規律辦事.教學的本質在于喚醒，教學的本體在于對話，教學的本然在于追求學生“自明”.數學教學離不開探究過程，通過問題驅動讓學生在做中學、學中做，充分發揮學生的主體作用，在本節課教學過程中也充分注意學生在獨立思考基礎上的合作交流，充分發揮學生的主觀能動性，凡是學生自己能做的，大膽放手讓他們獨立完成，教師不可越俎代庖，包辦代替.

3.2 優化教學設計必須篤行核心素養

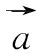
正所謂“三個理解百般好，核心素養不可少.抽絲剝繭拓思維，直擊內核顯真章”.