一道不等式證明的探究
?福建省莆田第六中學 李德琳
我們熟知的重要不等式結(jié)論“ex≥x+1,當且僅當x=0時等號成立”“l(fā)nx≤x-1,當且僅當x=1時等號成立”,經(jīng)常巧妙設置于題中,是破解一些與不等式有關(guān)的問題比較常用的重要結(jié)論.創(chuàng)設數(shù)列不等式的證明問題,是高考數(shù)學中比較常見的一類綜合交匯題,合理融合函數(shù)與方程、導數(shù)、數(shù)列、不等式及其證明等眾多知識,實現(xiàn)命題的綜合性、交匯性與創(chuàng)新性,倍受各方關(guān)注.
1 問題呈現(xiàn)
問題[陜西省咸陽市2022年高考模擬檢測(二)數(shù)學(理科)試題·21]已知函數(shù)f(x)=lnx-kx+1.
(1)若f(x)≤0恒成立,求實數(shù)k的取值范圍;
此題以含參函數(shù)所對應的不等式恒成立來巧妙創(chuàng)設情境,進而確定對應參數(shù)的取值范圍,在此基礎上構(gòu)建重要不等式結(jié)論“l(fā)nx≤x-1,當且僅當x=1時等號成立”,進而通過合理代換,結(jié)合放縮處理與變形,巧妙證明對應的數(shù)列不等式.
2 問題破解
方法1:分類討論法+裂項法1.
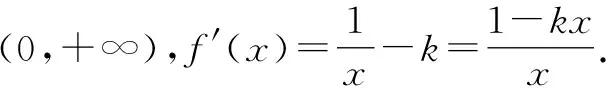
當k≤0時,f′(x)>0恒成立,則函數(shù)f(x)在(0,+∞)上單調(diào)遞增.
因為f(1)=-k+1>0,所以f(x)≤0不恒成立.
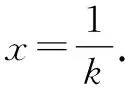
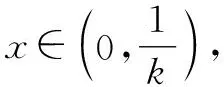
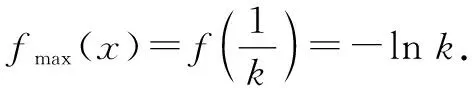
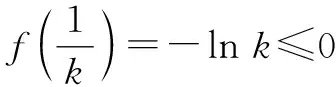
所以實數(shù)k的取值范圍是[1,+∞).
(2)證明:由(1)知,當k=1時,有不等式lnx≤x-1對任意x∈(0,+∞)恒成立,當且僅當x=1時等號成立.
所以x∈(1,+∞),lnx 當n≥3時, 解后反思:解決與含參函數(shù)有關(guān)的不等式問題,可以借助參數(shù)的不同取值情況加以分類討論;而證明不等式時,利用(1)中重要不等式結(jié)論加以轉(zhuǎn)化,通過合理放縮,借助裂項求和來轉(zhuǎn)化,實現(xiàn)對應不等式的證明與應用. 方法2:分離參數(shù)法+裂項法2. 若x∈(0,1),則g′(x)>0,函數(shù)g(x)單調(diào)遞增;若x∈(1,+∞),則g′(x)<0,函數(shù)g(x)單調(diào)遞減. 于是gmax(x)=g(1)=1. 結(jié)合f(x)≤0恒成立,可得k≥1. 所以實數(shù)k的取值范圍是[1,+∞). (2)證明:由(1)知,當k=1時,有不等式lnx≤x-1對任意x∈(0,+∞)恒成立,當且僅當x=1時等號成立. 所以x∈(1,+∞),lnx 解后反思:解決與含參函數(shù)有關(guān)的不等式問題,通過分離參數(shù),借助構(gòu)建函數(shù),通過確定函數(shù)的最值得以解決參數(shù)的取值范圍問題,也是解決此類問題比較常見的一種技巧方法;不等式證明中的不同放縮尺度以及對應的裂項求和處理,都是解決問題的重點,關(guān)鍵是合理配湊與巧妙轉(zhuǎn)化. 保持創(chuàng)新問題背景,借助不同數(shù)列不等式的給出,通過不同類型的參數(shù)代換處理,實現(xiàn)不同數(shù)列不等式的證明問題,拓展思維,倡導應用. 變式1已知函數(shù)f(x)=lnx-kx+1. (1)若f(x)≤0恒成立,求實數(shù)k的取值范圍; 解析:(1)同原問題中的解析(1),可得k≥1,所以實數(shù)k的取值范圍是[1,+∞). (2)證明:由(1)知,當k=1時,有不等式lnx≤x-1對任意x∈(0,+∞)恒成立,當且僅當x=1時等號成立. 所以x∈(1,+∞),lnx 令x=n2(n∈N*,n>1),代入lnx 變式2已知函數(shù)f(x)=lnx-kx+1. (1)若f(x)≤0恒成立,求實數(shù)k的取值范圍; 解析:(1)同原問題中的解析(1),可得k≥1,所以實數(shù)k的取值范圍是[1,+∞). (2)證明:由(1)知,當k=1時,有不等式lnx≤x-1對任意x∈(0,+∞)恒成立,當且僅當x=1時等號成立. 所以x∈(1,+∞),lnx 不妨令 變式3已知函數(shù)f(x)=lnx-kx+1. (1)若f(x)≤0恒成立,求實數(shù)k的取值范圍; 解析:(1)同原問題中的解析(1),可得k≥1,所以實數(shù)k的取值范圍是[1,+∞). (2)證明:由(1)知,當k=1時,有不等式lnx≤x-1對任意x∈(0,+∞)恒成立,當且僅當x=1時等號成立. 所以x∈(1,+∞),lnx ③ 另一方面,令x=n2(n∈N*,n>1),代入不等式lnx ④ 解后反思:根據(jù)重要不等式結(jié)論“l(fā)nx≤x-1,當且僅當x=1時等號成立”的分析與求解,再結(jié)合所要證明的數(shù)列不等式的形式,抓住數(shù)列中相關(guān)項的結(jié)構(gòu)特征,合理引入?yún)?shù)進行代換處理,結(jié)合不等式的性質(zhì)以及所要證明的不等式結(jié)構(gòu)的特征,巧妙放縮與轉(zhuǎn)化,從而實現(xiàn)數(shù)列不等式的證明與應用. (1)記憶二級結(jié)論,掌握基本方法. 重要不等式結(jié)論“ex≥x+1,當且僅當x=0時等號成立”或“l(fā)nx≤x-1,當且僅當x=1時等號成立”,是導數(shù)及其應用中比較常見的二級結(jié)論,特別在一些小題(選擇題或填空題)中,結(jié)合指數(shù)式或?qū)?shù)式的特征結(jié)構(gòu),利用相應的二級結(jié)論合理放縮,巧妙化歸轉(zhuǎn)化,使問題的求解更加直接、便捷,是破解一些與不等式有關(guān)的問題比較常用的重要結(jié)論與技巧策略. (2)巧妙參數(shù)代換,合理放縮處理. 涉及此類數(shù)列不等式的證明與應用,其實質(zhì)就是巧妙利用重要不等式結(jié)論“ex≥x+1,當且僅當x=0時等號成立”或“l(fā)nx≤x-1,當且僅當x=1時等號成立”,借助結(jié)論實質(zhì)結(jié)合數(shù)列不等式中相關(guān)的項加以合理參數(shù)代換,對比所證明不等式的結(jié)構(gòu)特征與結(jié)論,合理放縮處理,巧妙變形轉(zhuǎn)化,從而實現(xiàn)不等式的證明.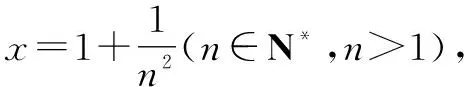
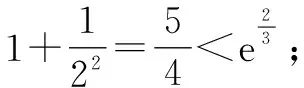
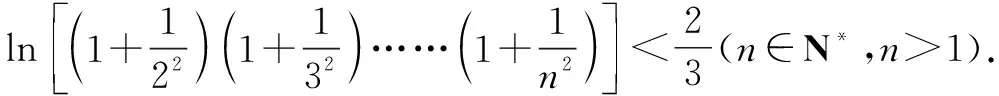
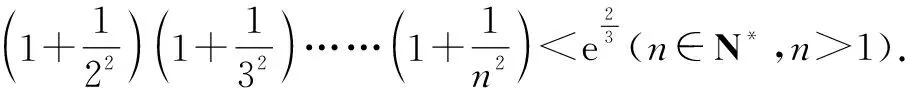
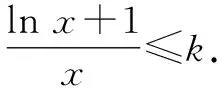
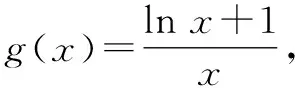
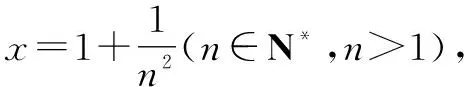
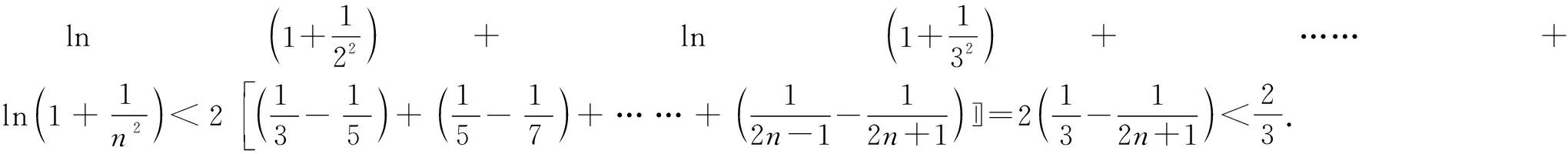
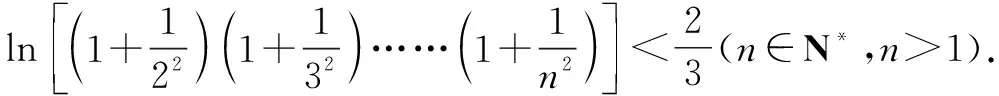
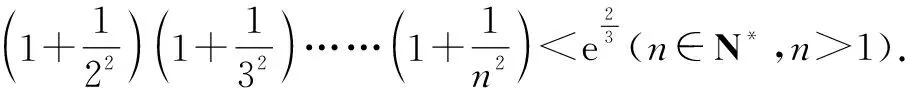
3 變式拓展
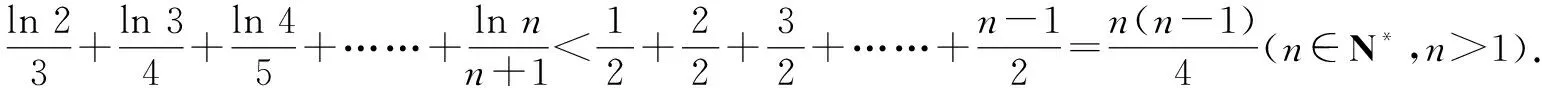
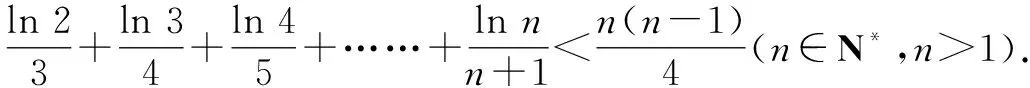
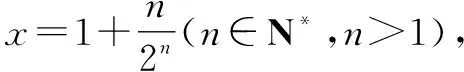
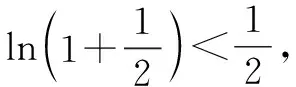
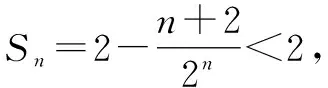
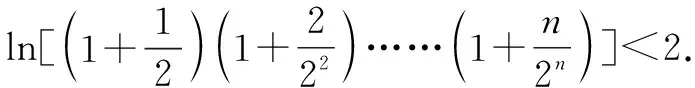
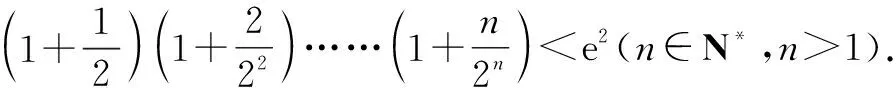
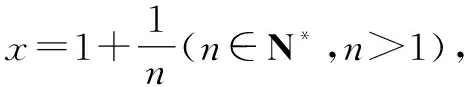
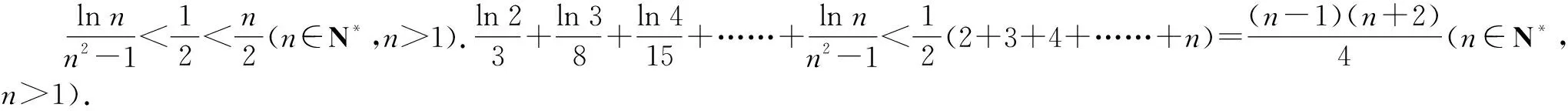
4 教學啟示

