例談目標函數法解答圓錐曲線最值問題的策略

?安徽省靈璧中學 高宗杰

與圓錐曲線相關的最值問題是高中數學常見的綜合性問題，構建目標函數求解圓錐曲線最值問題，是常見的解題方法之一，也是學生應該掌握的解題策略.筆者從不同例題的不同目標函數構建形式入手分析，分別闡述圓錐曲線最值問題求解的策略.

1 構建分式函數

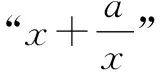
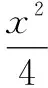
解：①當矩形的一邊與坐標軸平行時，可知矩形面積S=8.

②當矩形的一邊不與坐標軸平行時，由矩形和橢圓的對稱性，設其中一邊所在直線的方程為y=kx+m，則其對邊直線方程為y=kx-m.

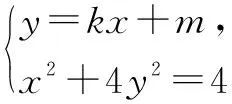
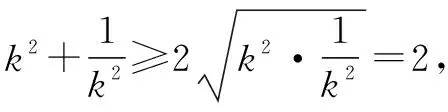
綜上所述，矩形面積的最大值為10，最小值為8.

2 構建二次函數

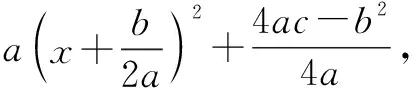
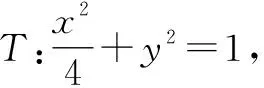
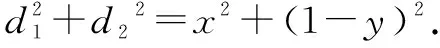
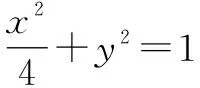
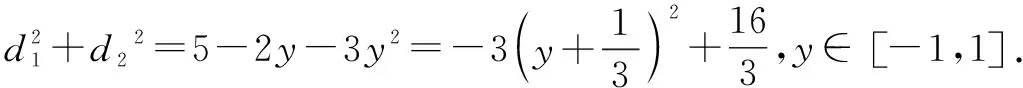
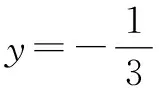
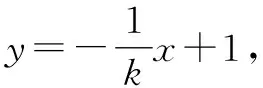
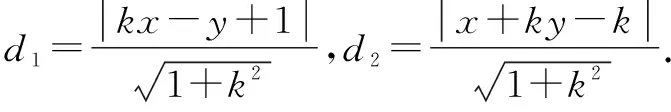
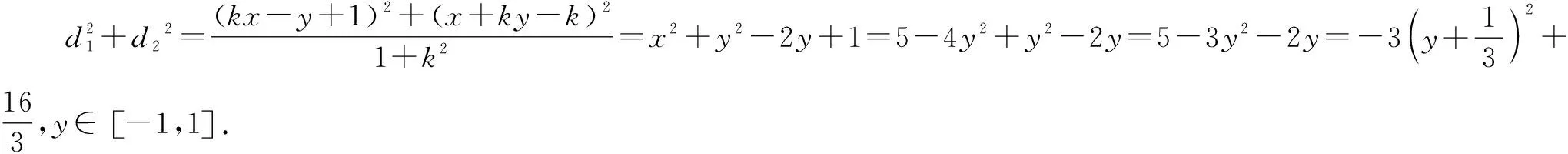
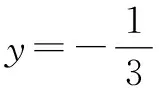
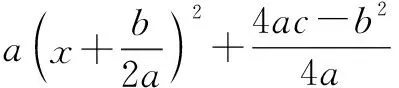
推廣已知P為拋物線y2=4x上的一點，Q為圓(x-6)2+y2=1上的一點，則|PQ|的最小值為______.

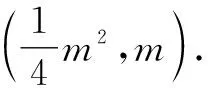
3 構建三角函數

當假設變量為角度時，構建的目標函數為三角函數，根據三角函數的有界性找到所求最值即可.解題時，首先找到需要假設的角度，其次表達所求問題，根據輔助角公式轉化為Asin(ωx+φ)+B的形式，從而求得最值.具體解題步驟和思路如例3所示.

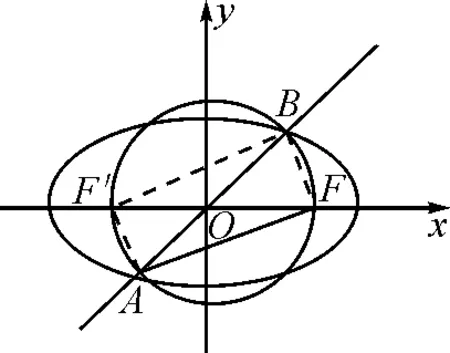
圖1

解：設橢圓的另一焦點為F′，連接AF′,BF′,BF,如圖1所示.四邊形AFBF′為矩形，可得|AB|=|FF′|=2c，|FA|=2c·cosα，|FB|=2c·sinα.

由橢圓定義，可得

|FA|+|AF′|=|FA|+|FB|=2a.

所以2c·cosα+2c·sinα=2a.

因此，離心率

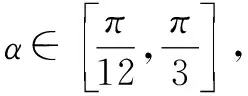
點評：當問題中未提及角度變量時，可以根據已知條件特征假設相關角θ，也可以用sinθ或cosθ表示相關點的坐標，進而用sinθ或cosθ表示所求的值，從而通過角θ的范圍，求得最解.如以下推廣例題，構建三角函數求問題的最值.

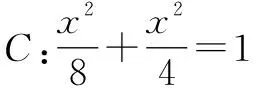
分析：圓(x-1)2+y2=1的圓心C(1,0)，半徑r為1.如圖2所示，連接QC,交AB于點H，可得H是線段AB的中點，且AB⊥QC.

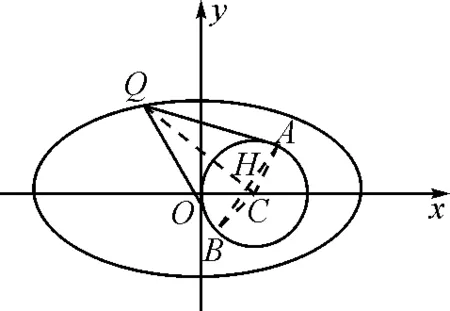
圖2

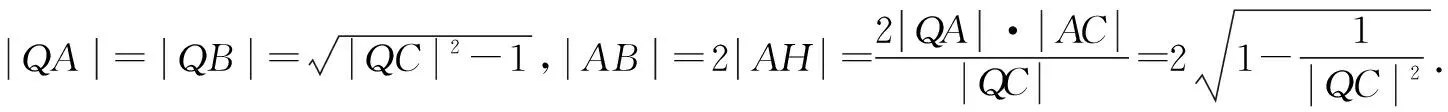
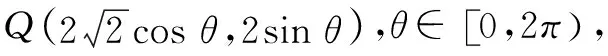
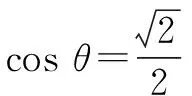
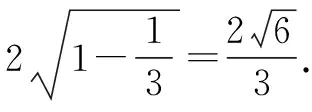
通過上述不同解題策略的介紹，不難發現構建目標函數求圓錐曲線的最值問題大致分為三種思路，其中三角函數、二次函數以及分式函數的構建都能夠有效求解問題.通過對這些解題思路的分析探究，啟示學生應該善于從試題中發現規律、總結解法，只有養成良好的學習習慣，才能收獲更多的積累.