牙輪鉆頭用單金屬密封瞬態啟動動力學模型與密封性能

馬 藝 陳宇濤 孟祥鎧 趙文靜 彭旭東

1.浙江工業大學機械工程學院，杭州，3100232.過程裝備及其再制造教育部工程研究中心，杭州，310023

0 引言

牙輪鉆頭是我國油氣勘探開發常見的破巖工具，適用于深部、超深部等地層。單金屬密封因結構簡單、耐磨損、占用空間小等特點，被廣泛應用于牙輪鉆頭軸承密封系統，在確保鉆頭長期使用方面起著關鍵作用。受鉆井環境、操作工況、地層特點及不可控因素等綜合影響，牙輪鉆頭在破巖鉆進過程中存在頻繁啟停現象，同時伴隨有劇烈振動[1-3]，尤其是在高壓條件下，單金屬密封的動態穩定性對牙輪鉆頭乃至整個鉆采系統的可靠性和安全性至關重要[4],因此，有必要開展啟動過程中牙輪鉆頭單金屬密封受振動激勵的瞬態動力學行為及密封性能的研究。

國內外學者主要對鉆頭金屬密封的穩態性能和結構優化開展了相關研究。張毅等[5-6]利用有限元分析方法對第二代單金屬密封(SEMS2)進行熱力耦合研究，分析了井下溫度和鉆井液壓力等對密封端面接觸壓力和泄漏率的影響，并以此為基礎開展了單金屬密封的多目標優化。ZHOU等[7]和ZHANG等[8]研究了雙金屬密封的接觸力學性能及壓差、壓縮比和熱負荷等對密封的影響，綜合分析了O形輔助密封圈的應力分布及變形狀態。馬藝等[9]基于密封系統的熱-流-固多場耦合狀態建立了單金屬密封(SEMS2)穩態綜合數學模型，研究了密封端面膜厚、溫升等隨運行工況的演化規律。目前對鉆頭密封動力學行為的研究較少，XIONG等[10-11]針對第一代單金屬密封(SEMS)建立了混合潤滑狀態下的非軸對稱數值模型及不考慮溫度和端面變形情況的動力學模型，研究了密封端面液膜壓力、厚度及泄漏量的時變特性，結果表明單金屬密封瞬態泄漏率、接觸應力等明顯增加。相對較為成熟的機械密封動力學分析思路和方法可在一定程度上為單金屬瞬態密封性能的研究提供借鑒。GREEN等[12]構建并求解了接觸式機械密封的潤滑控制方程和動力學方程，探究了密封環受軸向振動和跳動時的瞬態運動規律。孟祥鎧等[13]建立了描述機械密封瞬態啟停過程的動力學模型，研究了啟停過程中軸向跳動對機械密封浮動環動態特性的影響。徐魯帥等[14]建立了復雜擾變工況下非接觸式機械密封動態耦合數學模型，分析了變速及擾動下機械密封的瞬態響應及振動特性。

綜上所述，目前關于鉆頭密封的研究尚未充分考慮瞬時啟動與振動工況對牙輪鉆頭單金屬密封性能的影響，而且單金屬密封的動態特性與密封端面液膜狀態的耦合作用機制尚不明晰。本文建立牙輪鉆頭單金屬密封(SEMS2)瞬態特性綜合數學模型，探究瞬時啟動及振動工況下單金屬密封的動力學行為與密封性能，考察鉆頭轉速、軸向激勵對單金屬密封端面液膜形態、端面溫升及泄漏率、摩擦扭矩時變特性的影響規律，為鉆頭金屬密封系統的高效可靠設計提供參考。

1 計算模型

1.1 幾何模型

圖1為牙輪鉆頭單金屬密封裝配結構示意圖。單金屬密封系統由金屬動環、金屬靜環、O形圈、橡膠支撐環及軸頸組成，利用O形圈等輔助密封件的彈性支撐作用使金屬靜環與金屬動環緊密貼合。密封環內徑側介質為潤滑油，外徑側介質為鉆井泥漿，兩側密封腔保持一定壓差(Δp=0.3～0.7 MPa[15])，以防止泥漿侵入軸承。

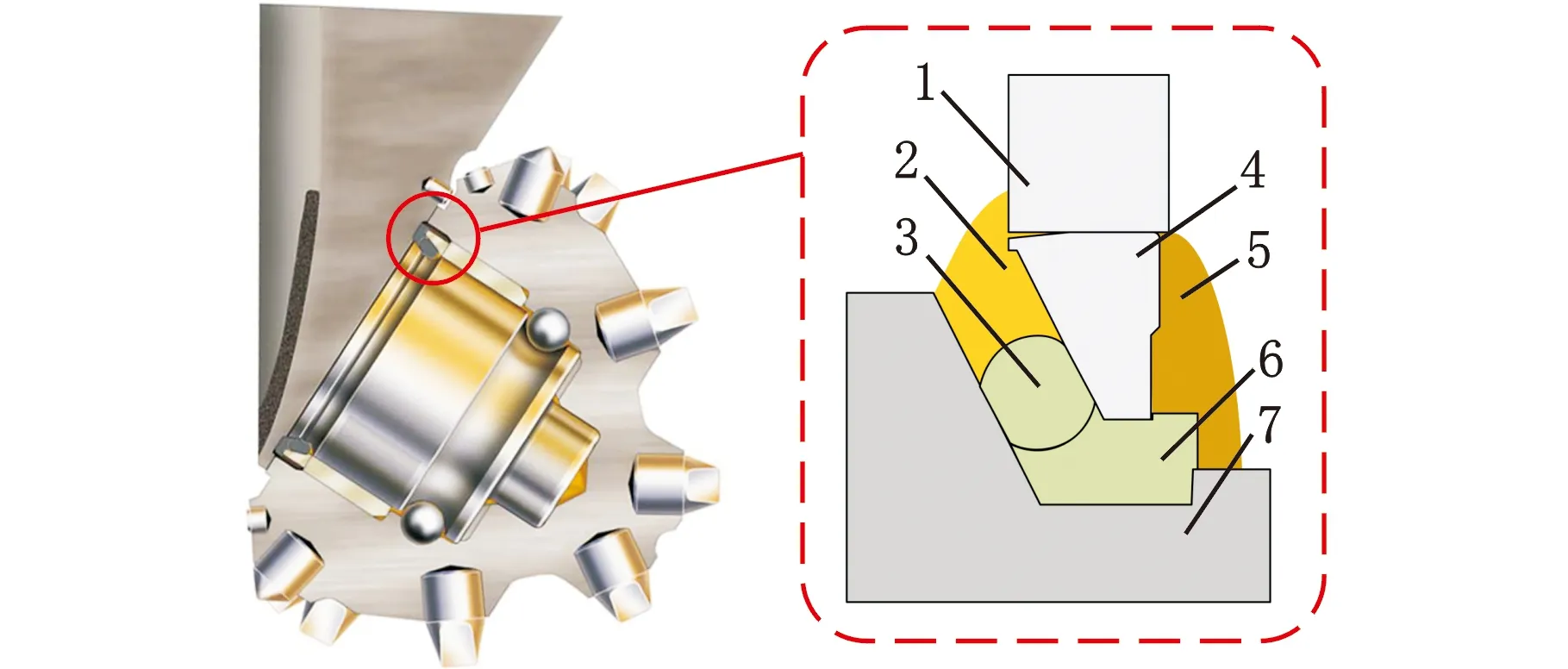
1.金屬動環 2.潤滑油 3.O形圈 4.金屬靜環 5.鉆井泥漿 6.橡膠支撐環 7.軸頸

1.2 數學模型

單金屬密封的端面潤滑特性、熱傳遞、端面變形和動態特性之間存在強耦合關系，因此，需綜合開展流體力學、接觸力學、傳熱學與動力學分析，從而建立單金屬密封瞬態特性綜合數學模型。

1.2.1端面潤滑

根據單金屬密封工作環境，作以下假設：①密封介質為牛頓流體；②金屬密封環為軸對稱模型，忽略周向變化；③忽略空化、慣性力對密封環的影響。

充分考慮表面粗糙度、擠壓效應、流量因子及接觸因子等影響，建立適用于單金屬密封混合潤滑狀態的控制方程：

(1)

式中，r為徑向位置；μ為液膜動力黏度；h為液膜厚度；pL為液膜壓力；t為時間；φr、φc分別為徑向流量因子和接觸因子[16]。

徑向流量因子φr采用下面經驗公式計算：

(2)

式中，γ為平面的表面特性，表示微凸體在x方向和y方向的數值比；C、λ分別為與γ相關的系數；σ為密封端面綜合粗糙度的均方根。

不失一般性，采用γ=1時的各項系數值，徑向流量因子φr可表示為

φr=1-0.9exp(-0.56h/σ)

(3)

接觸因子φc可表示為

(4)

由于溫度開高，流體性質發生明顯變化，故采用如下方程表征溫度T對流體黏度的影響[17]：

μ=μ0(T0/T)β

(5)

式中，T0為環境溫度；μ0為環境溫度下的流體黏度；β為黏溫系數。

1.2.2熱分析

單金屬密封的熱源主要來自兩方面：①動靜環相對轉動，端面間接觸部分產生接觸摩擦熱qf；②密封環對端面間液膜的黏性剪切作用，產生黏性剪切熱qv。熱流密度q的計算公式為

q=qf+qv

(6)

qf=fpcωr

(7)

(8)

式中，f為動摩擦因數；ω為動環旋轉角速度；pc為接觸壓力。

假設微凸體高度呈高斯分布，則接觸壓力可表示為[17]

(9)

式中，H為端面材料的壓縮強度。

忽略熱滯后，利用影響系數法[18]對端面溫度的變化進行求解。端面節點i處的溫度Ti表達式為

(10)

Ti=T0+δTi

(11)

式中，Tij為溫度影響系數，代表單位熱量作用在節點j時節點i處的溫升；qj為不同節點j處的熱流密度；δTi為節點i的溫度變化。

1.2.3端面變形

液膜壓力和接觸壓力分布都與膜厚密切相關，接觸壓力又強烈地依賴于密封面的熱、力變形。由于密封環端面變形非常小，故假定變形與作用力和熱流量成線性關系，采用影響系數法[18]求解端面變形量。利用ANSYS軟件建立單金屬密封有限元模型，分別對動靜環端面各節點施加單位力載荷和單位熱流量，組成力變形影響系數矩陣和熱變形影響系數矩陣，則節點i處兩個密封面的組合變形δi可表示為

(12)

式中，Lij、Rij分別為單位力、熱載荷作用在節點j時節點i處的變形量；Fj為作用在節點j上的力；Ci為環境壓力下鉆頭未啟動時節點i處的初始變形量。

膜厚分布可由如下方程獲得：

hi=hm+(δir+δis)max-(δir+δis)

(13)

式中，hm為不同時刻下的初始膜厚值，即平均膜厚；δir、δis分別為動靜環在節點i處的絕對變形量；(δir+δis)max為動靜環絕對變形的最大代數和；(δir+δis)為動靜環在節點i處的代數和。

1.2.4動態分析

鉆頭瞬態啟動及振動條件下，單金屬密封所受載荷不斷變化，靜環位置通過輔助密封件動態反饋調節，端面膜厚隨之變化。對單金屬密封系統動靜環進行簡化及受力分析，如圖2所示。

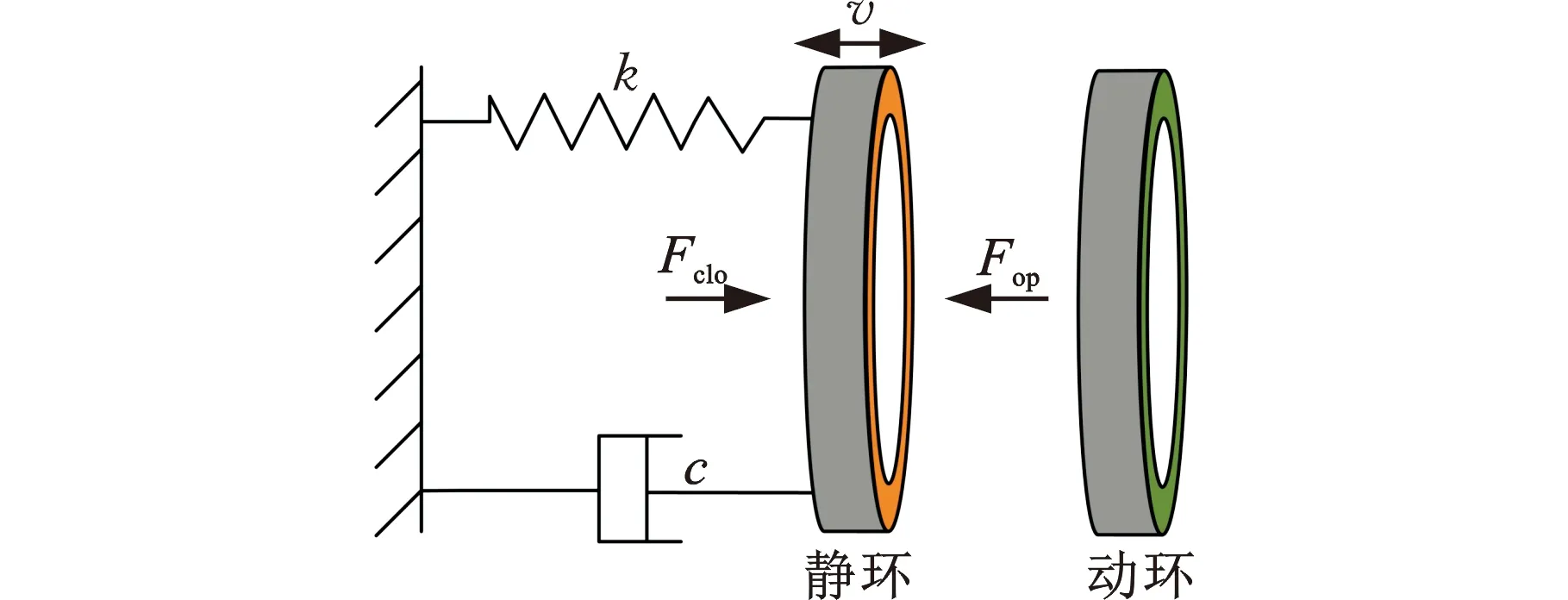
圖2 動力學分析示意圖

建立軸向擾動作用下金屬靜環的動力學方程：

(14)

式中，m為金屬靜環質量；k為輔助密封元件的軸向剛度系數；c為輔助密封元件的軸向阻尼系數；Fclo為閉合力；Fop為開啟力；Fa為振動引起的軸向載荷。

閉合力由內外介質壓力及輔助密封件對金屬靜環的作用共同組成，即靜接觸壓力psc對密封端面的作用力，計算公式為

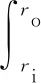
(15)

式中，ri為密封環內徑；ro為密封環外徑。

開啟力由接觸力Fc和液膜力FL共同組成，可表示為

Fop=FL+Fc

(16)

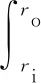
(17)

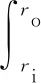
(18)

對于振動引起的軸向載荷，因載荷頻率f與角速度ω有關，即f=ω/(2π)，故假定波動為正弦形式[19]，則有

Fa=Asinωt

(19)

式中，A為載荷幅值。

采用Newmark法中的平均加速度法逐步積分求解上述動力學方程[20]。在每一時間步，采用二分法求得當前時間步的密封性能參數和動力學特性參數，并為下一時間步的計算提供初始值。計算公式為

(20)

(21)

式中，α=0.25；γ=0.5。

1.3 計算流程

瞬時啟動過程單金屬密封動力學特性的計算流程如圖3所示，采用有限差分法結合多重數值迭代算法進行聯合求解。

2 計算參數及模型驗證

2.1 計算參數

本文計算的基本參數[21]如表1所示。

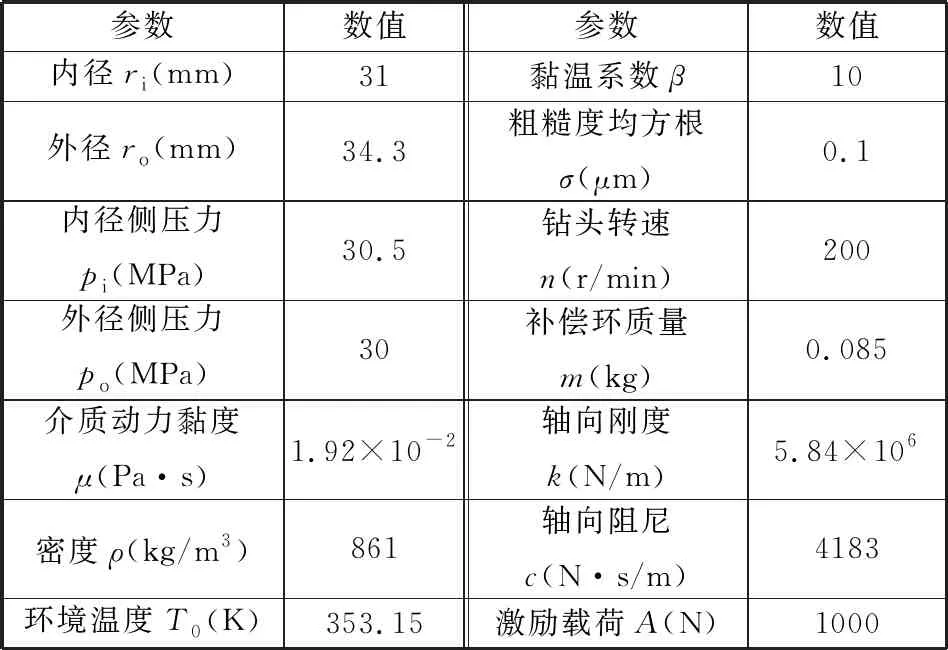
表1 單金屬密封幾何參數及工況參數

啟動階段鉆頭所處環境壓力不變，角速度隨時間變化采用定加速度線性增加的方式實現[22]，表達式為

(22)

式中，ωend為啟動時最終角速度；ta為加速時間。

鉆頭啟動過程中角速度ω和激勵載荷Fa的變化規律如圖4所示。t=0～1 s為啟動階段，角速度以線性形式增加，激勵載荷頻率隨角速度ω逐漸增大；t=1～2 s為恒轉速階段，轉速和激勵載荷頻率保持不變。當t>2 s時，單金屬密封繼續保持上述恒轉速穩定波動狀態，為更直觀地體現單金屬密封瞬時啟動階段各參數變化，后續均截取前2 s時間段開展分析。

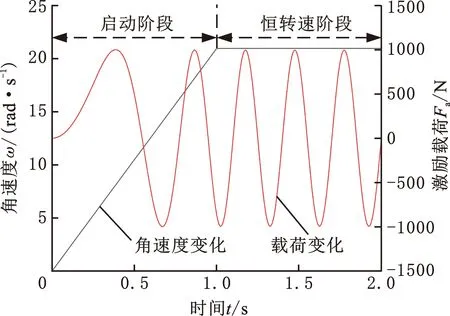
圖4 啟動過程角速度和激勵載荷變化規律

2.2 模型驗證

為驗證本文瞬態模型和方法的準確性，采用文獻[23]中的參數進行數值計算，并將計算結果與文獻中結果進行比較，分析多個時刻(t=1，5，10，20 s)密封端面液膜壓力與厚度的分布規律，如圖5所示。結果表明，4個時刻本文模型所得液膜壓力pL和液膜厚度h的徑向分布趨勢與文獻[23]所得趨勢均一致。本文計算值與文獻值吻合較好，整體上略小于文獻值。由圖5可知，本文模型所得密封端面液膜壓力、液膜厚度和文獻值的相對誤差均在t=20 s時、徑向位置r=60.8 mm處達到最大，分別為7%和9%。因此，本文建立的綜合數學模型能夠較好地預測啟動瞬時密封系統的動力學特性。

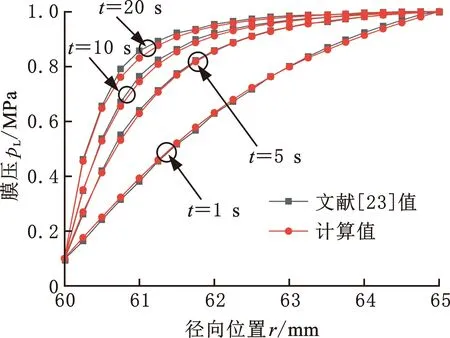
(a) 液膜壓力對比

3 結果分析和討論

3.1 啟動過程單金屬密封動態特性

3.1.1液膜演化規律

圖6為啟動過程中單金屬密封端面液膜厚度三維分布及時變曲線。由圖6a可以看出，在初始t=0時刻，密封端面膜厚沿徑向逐漸增大，呈發散型密封間隙。這是因為受高壓下靜環內側O形圈變形影響，單金屬密封端面接觸壓力呈內徑側高外徑側低的分布趨勢。聯合式(4)分析可得，密封區域內徑處膜厚值最小(0.248 μm)且h<3σ，微凸體會發生接觸，處于混合潤滑狀態；外徑處膜厚值最大(0.381 μm)且h>3σ，處于流體潤滑狀態。瞬態工況下密封端面發散型膜厚分布趨勢保持不變，但膜厚數值不斷變化。由圖6b可以看出，在t=0～1 s啟動階段，端面最大、最小膜厚波動頻率逐漸增加，波動幅度受轉速增加和載荷激勵影響擾動明顯。之后在t=1～2 s恒轉速階段，端面膜厚均呈周期性正弦形變化，靜環在閉合力、開啟力和軸向激勵載荷的共同作用下逐漸達到動態平衡，密封端面形成相對穩定的楔形振蕩間隙，但密封間隙內流體狀態始終為層流。相對而言，恒轉速階段密封端面最大膜厚的振幅可達最小膜厚振幅的2倍，容易加劇潤滑油的泄漏。

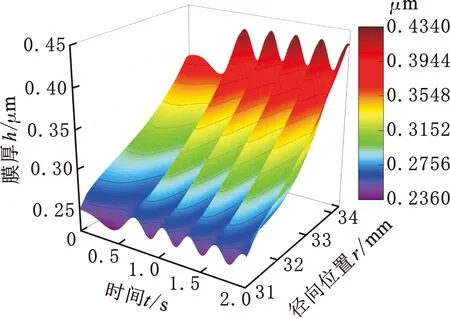
(a) 膜厚三維分布

選取初始t=0時刻(t0)及各特征波峰波谷(t1～t5)作為代表性瞬態時刻(圖6b)，分析不同時刻下單金屬密封端面液膜壓力(簡稱“膜壓”)與接觸壓力的徑向分布，如圖7所示。t0時刻密封端面膜壓沿徑向線性減小，與膜厚分布呈相反趨勢。隨著鉆頭的啟動以及激勵載荷的不斷作用，密封端面徑向膜壓分布逐漸演變成“上凸”—“下凹”—“上凸”的循環變化模式。在轉速穩定后，端面膜壓保持周期性變化且波動幅值更大，尤其在徑向位置r=32.4 mm處膜壓振幅最為明顯，最高可達7.7 MPa。這是因為持續的激勵載荷使得液膜受到擠壓作用，當密封環相互遠離時，膜壓減小，反之膜壓增大。由圖7b可知，不同時刻下接觸壓力始終在密封環內徑處(r=31 mm)達到最大值，尤其在啟動過程中(t1時刻)可達18.6 MPa，而在外徑側，由于微凸體不直接接觸，密封環完全由液膜壓力承載，因此，啟動過程中單金屬密封內徑側潤滑油難以順利進入密封間隙，潤滑狀態進一步惡化。

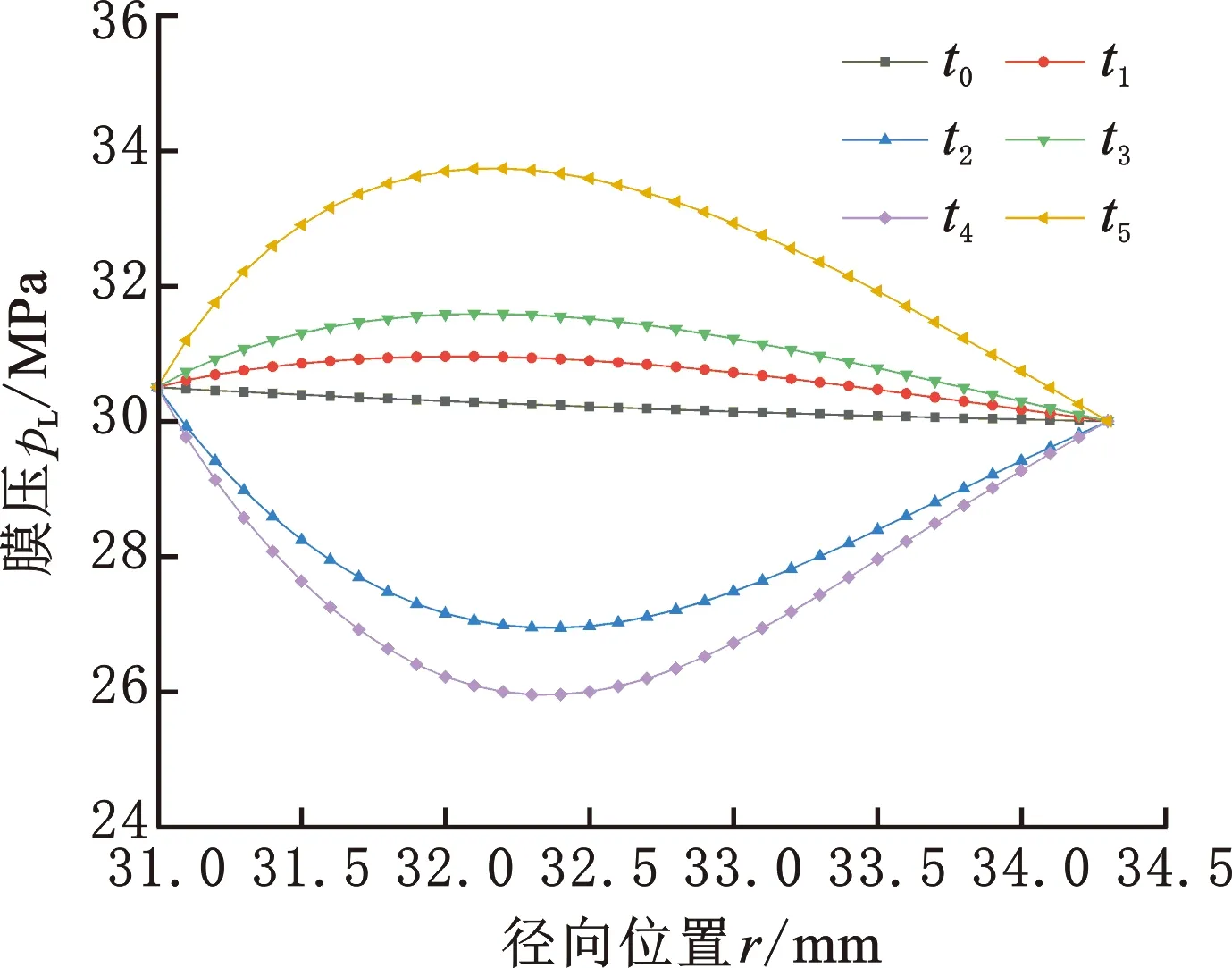
(a) 液膜壓力

3.1.2溫升時變特性

圖8為啟動過程中單金屬密封端面溫升ΔT時變曲線和瞬時溫升徑向分布曲線。可以看出，初始t0時刻密封端面溫度為環境溫度T0。密封端面溫升在鉆頭啟動階段呈波動增長趨勢，并在進入恒轉速階段后振蕩幅值差異性更加明顯，端面最大溫升振幅達到最小溫升振幅的2.3倍。因端面內徑處始終承受大部分接觸壓力，而外徑處接觸壓力為0，所以各時刻端面溫升在靠近內徑側(r=31.4 mm)和外徑處分別達到最大、最小值，在恒轉速t5時刻端面徑向溫差可達5.5 K。

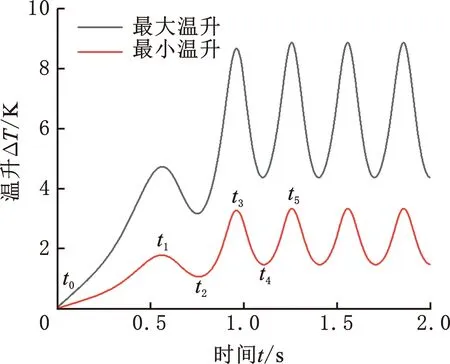
(a) 最大、最小溫升

圖9為不同時刻密封動靜環整體溫度分布云圖。以密封環端面最大溫升所在徑向位置r=31.4 mm為中心，隨著熱量向密封環主體不斷傳遞，動靜環溫度逐漸降低，最低溫度位于動環與牙輪鉆頭的接觸邊界，基本與環境溫度持平。靜環相比于動環整體溫升更為明顯。

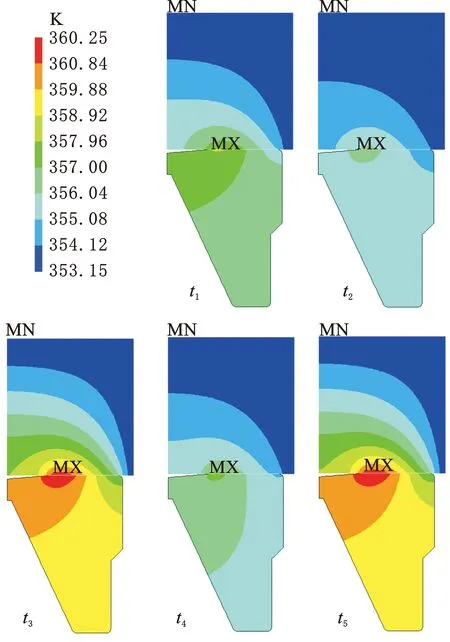
圖9 密封環溫度分布云圖

3.1.3動態密封性能

圖10所示為啟動過程中單金屬密封泄漏率與摩擦扭矩的變化規律。鉆頭啟動瞬時摩擦扭矩發生階躍性變化，并逐漸波動至振幅約為5 N·m的相對穩定狀態。隨著鉆頭的啟動，單金屬密封泄漏率的振動頻率和幅值逐漸增大，且遠超穩態泄漏率(0.0135 mL/h)。原因在于，一方面轉速的提高導致端面溫升逐漸增加，潤滑油黏度下降；另一方面受到軸向激勵的影響，密封端面外徑側液膜壓差增大，對密封端面間液膜產生擠壓效應。在啟動和恒轉速階段，泄漏率均呈正負交替的波動狀態：泄漏率為正值時，密封內徑側的潤滑油向外徑側泄漏；泄漏率為負值時，密封外徑側的泥漿極易侵入密封間隙。即振動工況下單金屬密封端面磨損加劇，更易失效，進而影響牙輪鉆頭的使用壽命。

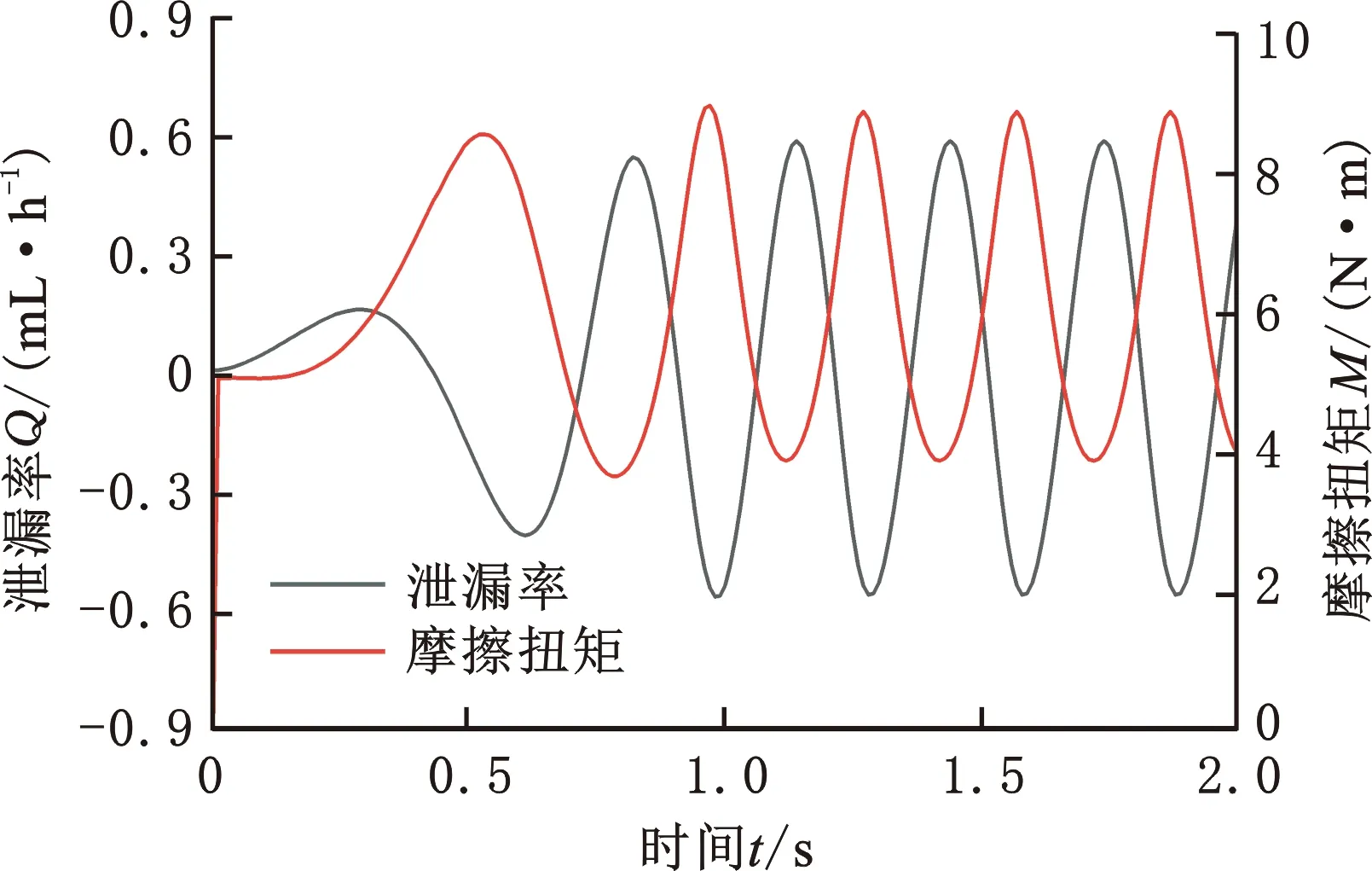
圖10 泄漏率和摩擦扭矩隨時間的變化規律

3.2 鉆頭轉速對密封動態特性的影響

保持啟動轉速趨勢不變，研究鉆頭最終穩定轉速n分別為100，200，400，600 r/min時單金屬密封端面平均膜厚和最大溫升的變化規律，如圖11所示。由圖11a可以看出，隨著鉆頭轉速的增加，啟動和恒轉速階段密封端面平均膜厚波峰值保持不變，而振動幅度逐漸減小且頻率明顯增加。這是因為當轉速增大時，端面膜厚沿徑向發散程度增加，液膜承載能力提高，使得密封環在相同的激勵下更快進入穩定振動狀態。即適當增加轉速，可改善密封界面潤滑狀態，提高密封穩定性。密封端面最大溫升始終靠近內徑側(r=31.4 mm)，但數值及變化梯度變化明顯。由圖11b可以看出，密封端面間的接觸摩擦熱和黏性剪切熱隨轉速增大而增加，啟動階段端面最大溫升整體大幅波動攀升，至恒轉速階段后振動頻率和幅度均明顯增加，鉆頭轉速n=600 r/min時的振動幅值約為n=200 r/min時振動幅值的3倍。

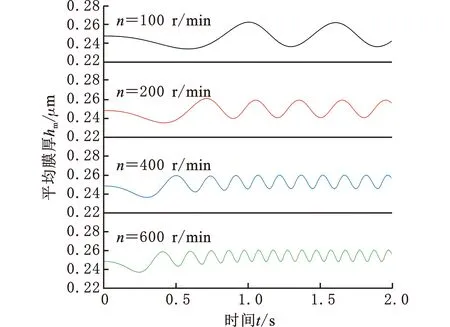
(a) 平均膜厚

圖12為不同鉆頭轉速下單金屬密封泄漏率和摩擦扭矩的時變曲線。由圖12a可以看出，在啟動初步階段，低轉速下密封界面泄漏率變化緩慢；隨著轉速不斷增加，密封端面介質黏度降低，泄漏率振動頻率和幅值逐漸增加，至恒轉速階段后，轉速n=600 r/min的瞬時最大泄漏率增至n=200 r/min的2.5倍。由圖12b可以看出，低轉速啟動時，摩擦扭矩振幅隨轉速變化并不明顯，而在n≥400 r/min時，摩擦扭矩幅值隨著轉速增大逐漸減小。這與鉆頭轉速增加所導致的膜厚增大有關，密封端面間特別是內徑處接觸壓力的減小使得摩擦扭矩降低。

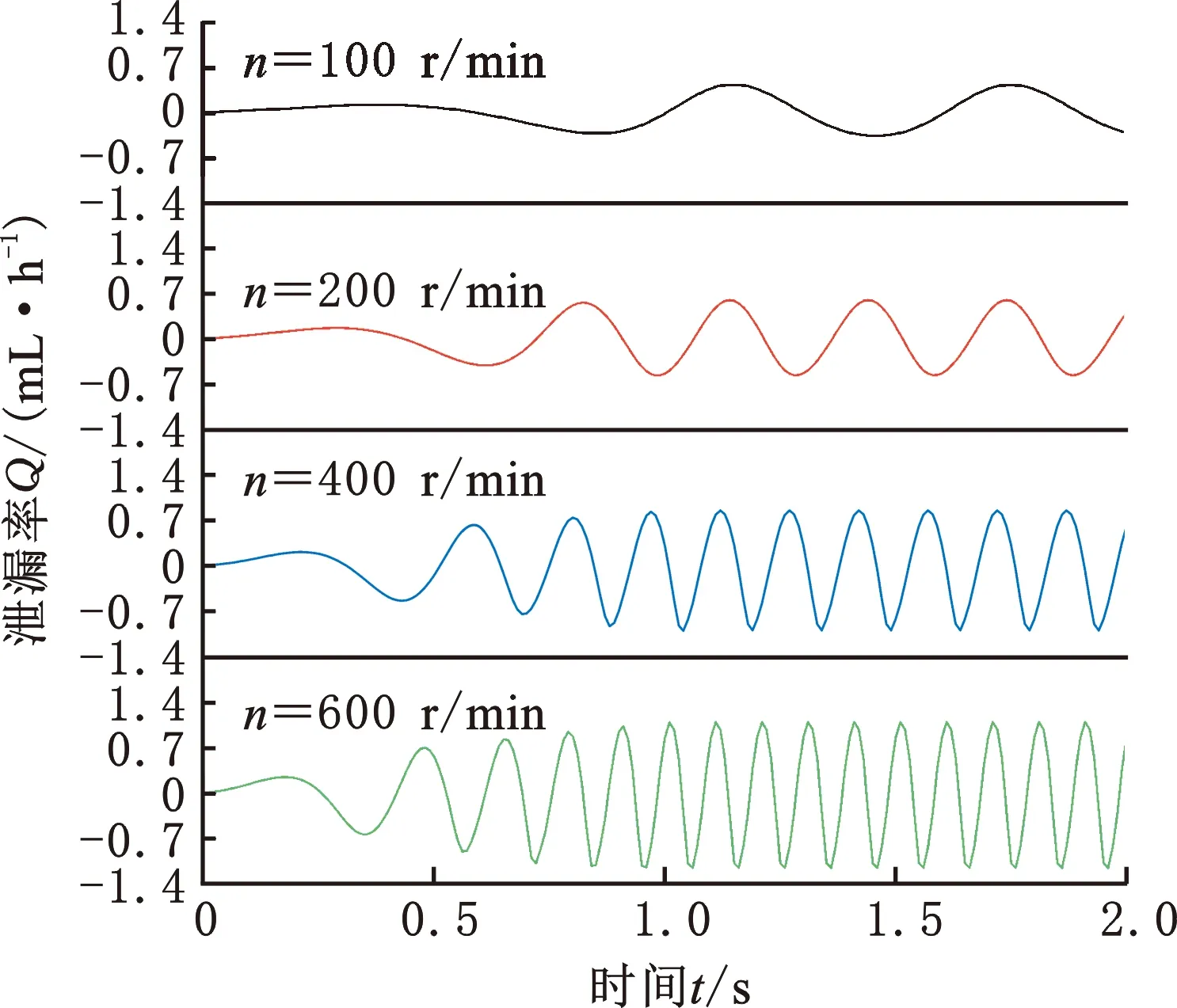
(a) 泄漏率

3.3 軸向激勵對密封動態特性的影響

研究軸向激勵載荷Fa分別為500，1000，500，2000 N時單金屬密封端面平均膜厚和最大溫升的變化規律，如圖13所示。可以看出，不同激勵載荷下密封端面平均膜厚和最大溫升的振動頻率及所處徑向位置均保持不變，單金屬密封的穩定性相對較好。在啟動階段，平均膜厚振幅隨軸向激勵載荷增大而明顯增大，且因慣性作用，它與恒轉速階段振幅差異更加明顯。由于動靜環貼合瞬間摩擦熱增加，端面最大溫升振幅隨軸向激勵載荷增大呈振蕩遞增至穩定的變化趨勢。在恒轉速階段，端面平均膜厚和最大溫升波形均隨軸向激勵載荷增大而上移，這是因為高激勵載荷作用下密封環接觸壓力和力變形增大所致。

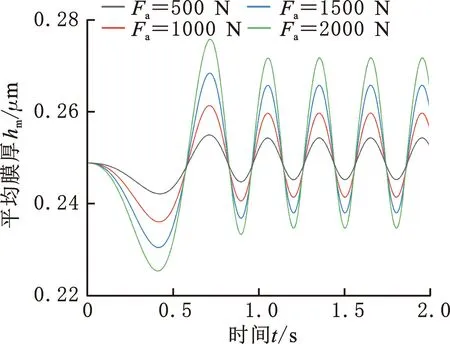
(a) 平均膜厚

圖14為不同軸向激勵載荷下單金屬密封泄漏率和摩擦扭矩的時變曲線。可以看出，隨著軸向激勵載荷增大，泄漏率和摩擦扭矩的波動幅值隨之增至穩定，此時Fa=2000 N時的最大泄漏率和摩擦扭矩可達Fa=500 N時的4.1倍和1.8倍。在恒轉速階段，泄漏率仍呈正負對稱交替式變化，而摩擦扭矩曲線則隨軸向激勵載荷增大而上移，這與密封端面平均膜厚變化相對應。因此，軸向激勵對單金屬密封動態穩定性影響顯著，進而影響牙輪鉆頭的可靠工作。

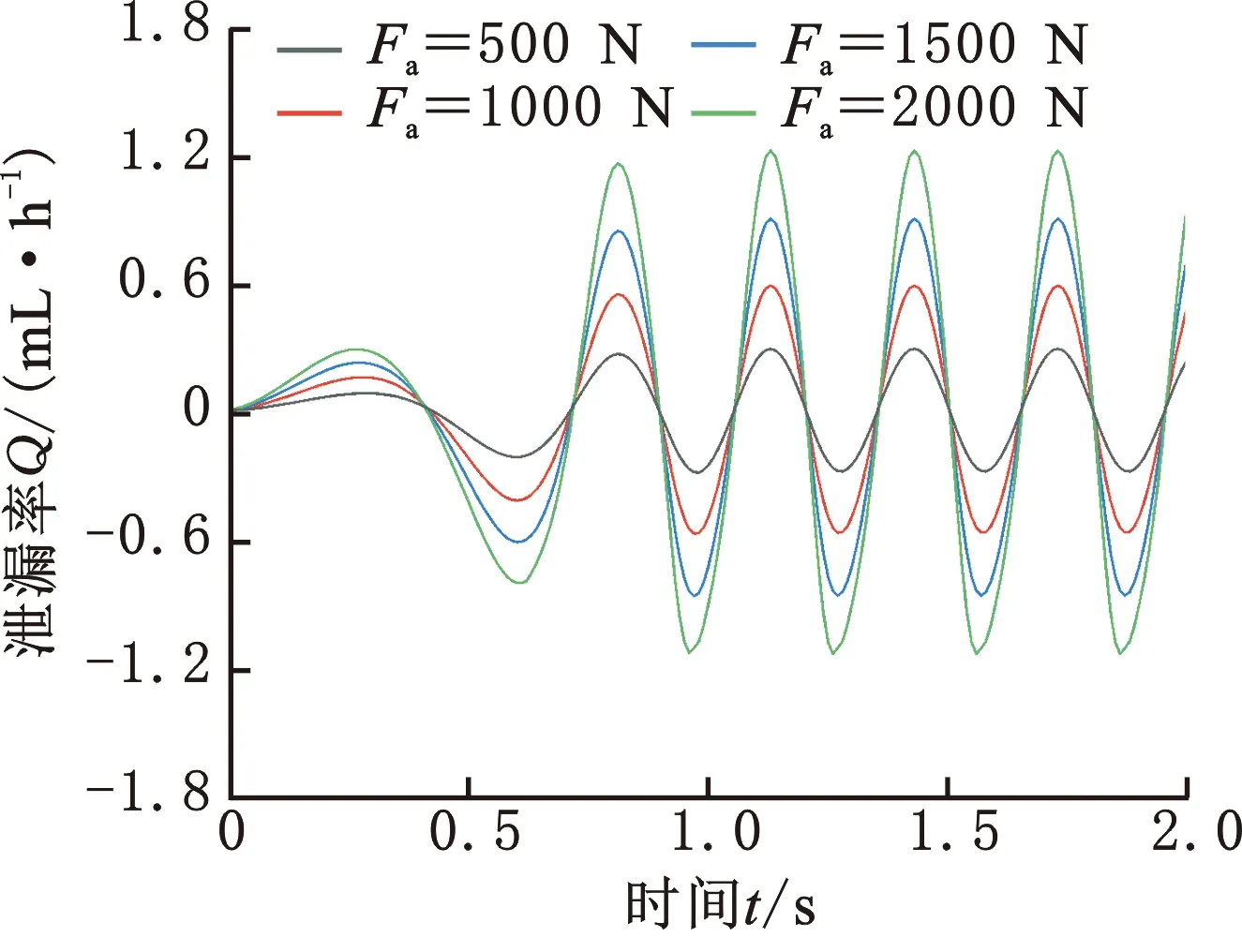
(a) 泄漏率

4 結論

(1)高壓(p0=30 MPa)下單金屬密封端面液膜沿徑向呈發散型間隙分布，由內徑側的混合潤滑狀態逐漸過渡為外徑側的流體潤滑狀態；鉆頭啟動至恒轉速過程中，端面膜厚波動頻率逐漸增加，最終穩定呈周期性正弦型變化，且液膜發散程度隨鉆頭轉速增加而增大，液膜承載能力有所提高。

(2)鉆頭啟動時單金屬密封端面溫升振蕩增加，徑向溫升變化梯度逐漸增大，分別在靠近內徑r=31.4 mm處和外徑處達到端面最大和最小溫升；隨著轉速和軸向激勵載荷增大，密封端面間接觸摩擦熱和黏性剪切熱增加，端面溫升波動振幅明顯增大。

(3)在鉆頭啟動和振動共同作用下，高轉速啟動時的摩擦扭矩幅值隨轉速增大逐漸減小；單金屬密封瞬時泄漏率呈正負交替波動狀態，幅值遠大于穩態泄漏率，特別是當泄漏率為負值時，密封外徑側的泥漿極易侵入密封間隙，而且該現象隨鉆頭轉速和軸向激勵載荷增大顯著加劇，單金屬密封性能進一步惡化。