帶卸荷板的大圓筒結構受力特性分析
郭夢圓,覃 杰,陳良志
(中交第四航務工程勘察設計院有限公司,廣東 廣州 510290)
大圓筒結構作為應用廣泛的重力式碼頭結構之一,具有節(jié)省混凝土、穩(wěn)定性好等優(yōu)點[1]。目前關于大圓筒結構的研究多圍繞大圓筒結構整體穩(wěn)定性、位移分析等開展,大部分沒有考慮上部卸荷板及其荷載[2-5]。然而,隨著船型和港口吞吐能力的增大,大量港口大力發(fā)展集裝箱運輸業(yè)務,將老碼頭進行升級改造的情況愈加普遍,也導致原結構所受的岸橋荷載顯著增大[6]。本文運用有限元軟件,建立帶卸荷板的大圓筒整體模型,研究岸橋荷載、波浪力、堆載土壓力分別作用下大圓筒的內(nèi)力特性[7]。
1 工程概況
某碼頭升級改造工程,原結構為重力式結構,采用無底薄壁大圓筒連片式布置,圓筒外徑為18.0 m、壁厚0.34 m,采用C40混凝土。圓筒外趾懸挑80 cm,底高程為-15.1 m,頂高程為3.0 m。圓筒頂上為現(xiàn)澆鋼筋混凝土卸荷板,采用梁肋式結構,由1根前軌道梁、1根肋梁、2根橫梁及底板組成。大圓筒碼頭結構斷面及卸荷板見圖1。
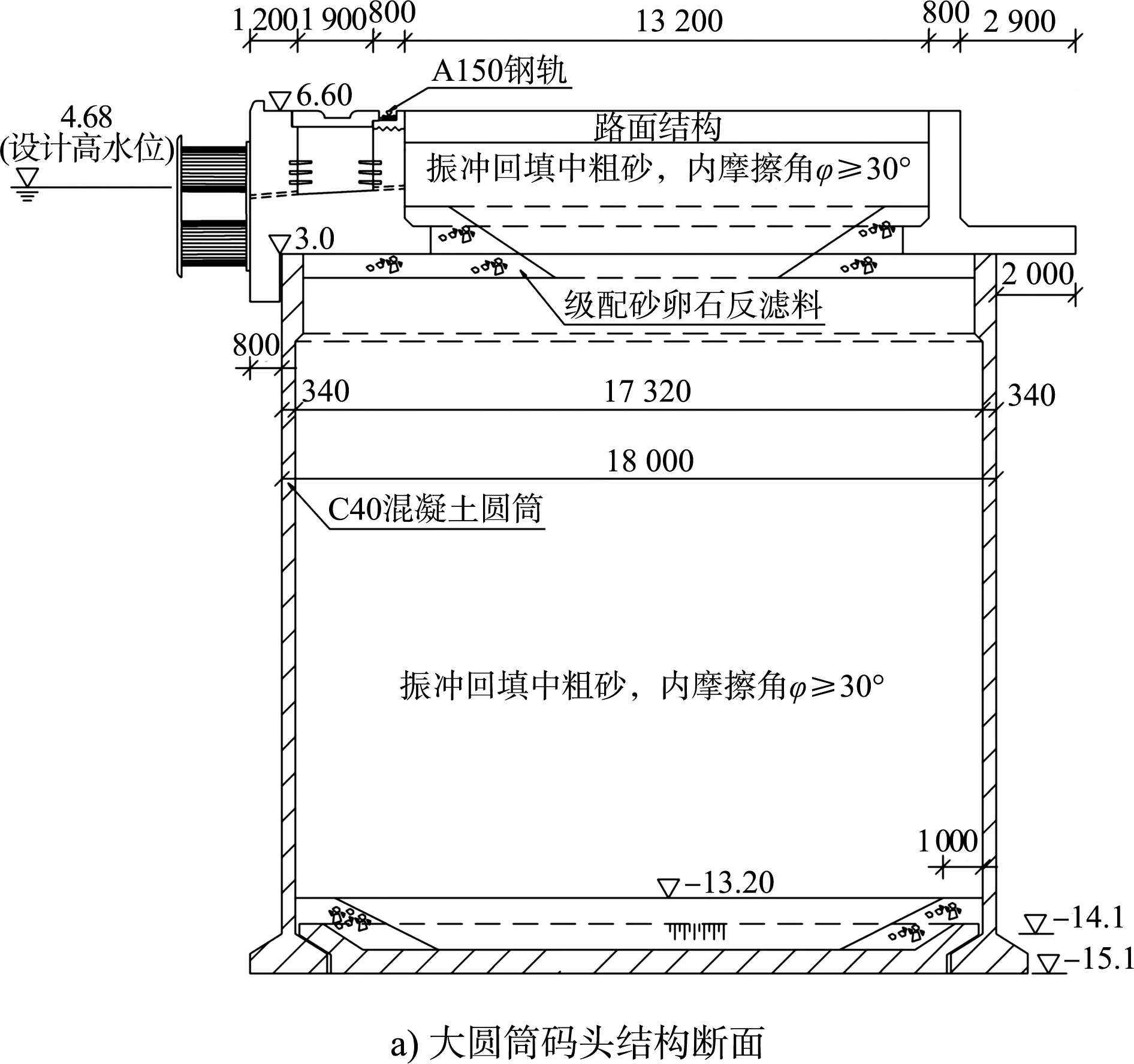
圖1 大圓筒碼頭結構斷面及卸荷板平面(高程:m;尺寸:mm)
2 計算條件
2.1 計算水位及波浪荷載
計算工況采用設計高水位+50 a一遇波浪作用條件,最不利波向為SSW向,設計高水位為4.68 m,設計低水位為0.40 m,平均潮差3.38 m。設計波浪條件為:波向SSW向,重現(xiàn)期50 a,設計高水位,波高H1%為3.78 m,平均周期Tm為7.5 s,波長L為78.7 m。
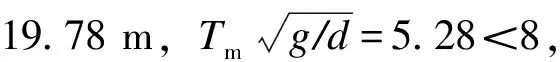
2.2 碼頭面均載及工藝荷載
碼頭面均載取40 kPa。裝卸機械采用自動化雙小車岸橋,支腿4個,10個輪/支腿,平均輪距1.23 m,軌距35 m、基距14 m[9]。岸橋預埋件受力見表1。
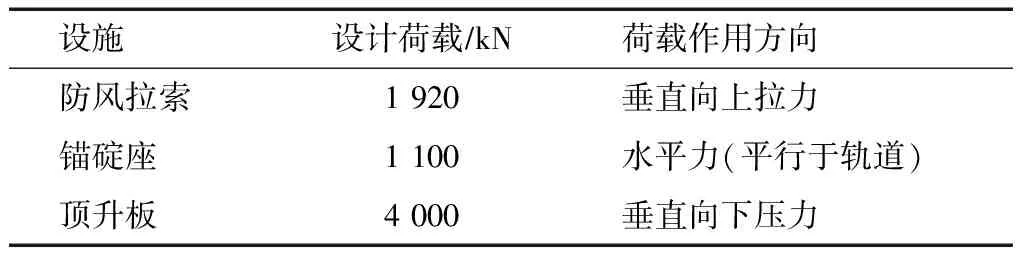
表1 岸橋預埋件荷載
考慮非工作狀態(tài)下岸橋荷載更大,因此計算工況選擇岸橋非工作狀態(tài)。在海側或陸側風荷載作用下,作用在碼頭結構上的岸橋荷載之間存在組合,在計算中進行考慮。分項系數(shù)取1.5。
2.3 貯倉壓力及土壓力
貯倉壓力按照文獻[7]計算,分項系數(shù)取1.35。土壓力分為碼頭面均載引起的可變土壓力(簡稱“堆載土壓力”)和回填料引起的永久土壓力(簡稱“填料土壓力”)。卸荷板以下的土壓力計算根據(jù)文獻[7]進行部分折減:對卸荷板,M點以上的土壓力可不計卸荷板底面以上重力的影響,N點以下的土壓力按無卸荷板的情況計算,M、N之間按直線過渡。分項系數(shù)取1.35。
2.4 荷載組合及施加方式
本文對比研究岸橋荷載、波浪力、堆載土壓力作用下的結構受力特性,其余荷載在計算時均施加在結構上。考慮到大圓筒之間有倒濾結構,波浪力、土壓力的添加范圍分別為大圓筒波浪側、土側154°圓心角;貯倉壓力施加在大圓筒內(nèi)壁,范圍為整個圓周。它們的作用范圍見圖2。
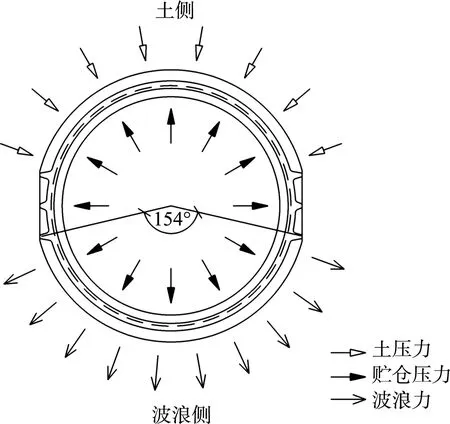
圖2 波浪力、貯倉壓力、土壓力作用范圍
前墻波浪壓強分布①、填料土壓強分布②見圖3。
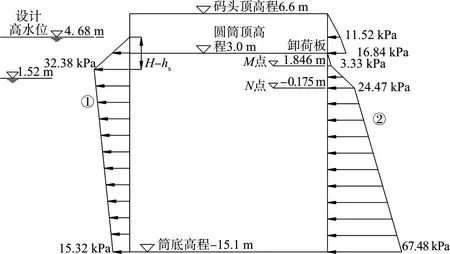
圖3 碼頭墻面波浪壓強和填料土壓強分布
3 有限元模型
因上部卸荷板受到自身重力及作用在卸荷板上的荷載(岸橋荷載、系纜力等),很難對其簡化作用在圓筒上,故將卸荷板與大圓筒整體建模。運用有限元軟件建立帶卸荷板的大圓筒結構三維模型。本構模型采用線彈性模型,計算中模型結構參數(shù)取彈性模量E=32.5 GPa,泊松比μ=0.2。卸荷板采用實體單元建立,下部大圓筒結構采用板單元建立,大圓筒底趾采用梁單元建立。模型邊界條件為大圓筒底邊固定,卸荷板與大圓筒之間運用多點約束方法進行實體-殼裝配,以模擬卸荷板與大圓筒之間的剛性約束。
網(wǎng)格劃分后的大圓筒結構模型見圖4,其中x軸正向為土側、負向為波浪側。由于大圓筒頂端向下2.1 m內(nèi)寬度加厚為0.54 m,故將圓筒分為兩部分:上部壁厚為0.54 m的圓筒頂端和下部壁厚為0.34 m的大圓筒進行結果分析。
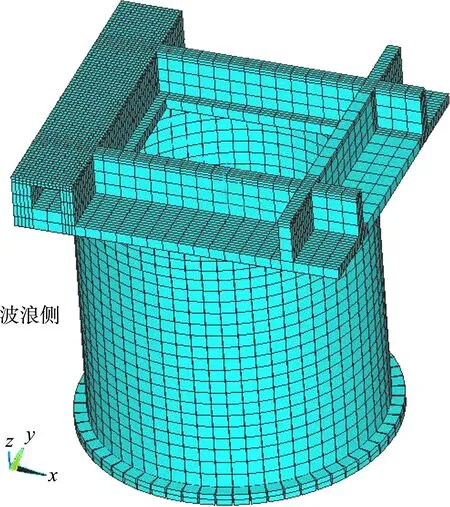
圖4 大圓筒結構計算模型
4 結果分析
不同荷載作用下大圓筒整體結構von Mises等效應力分布云圖見圖5。

圖5 不同荷載作用下大圓筒等效應力分布云圖
由圖5可知,岸橋荷載作用下,最大等效應力位于頂升荷載作用位置,為40 MPa,其余部位應力不超過9 MPa,而在自身重力、波浪荷載、堆載土壓力作用下,最大應力出現(xiàn)在筒兩端的筒壁內(nèi)側,約為7 MPa。可見岸橋荷載對大圓筒整體結構應力分布影響很小。
4.1 岸橋荷載
在岸橋荷載作用組合中,頂升荷載影響最大。圓筒內(nèi)力結果見表2,豎向彎矩分布云圖見圖6。

表2 岸橋荷載作用下大圓筒內(nèi)力結果
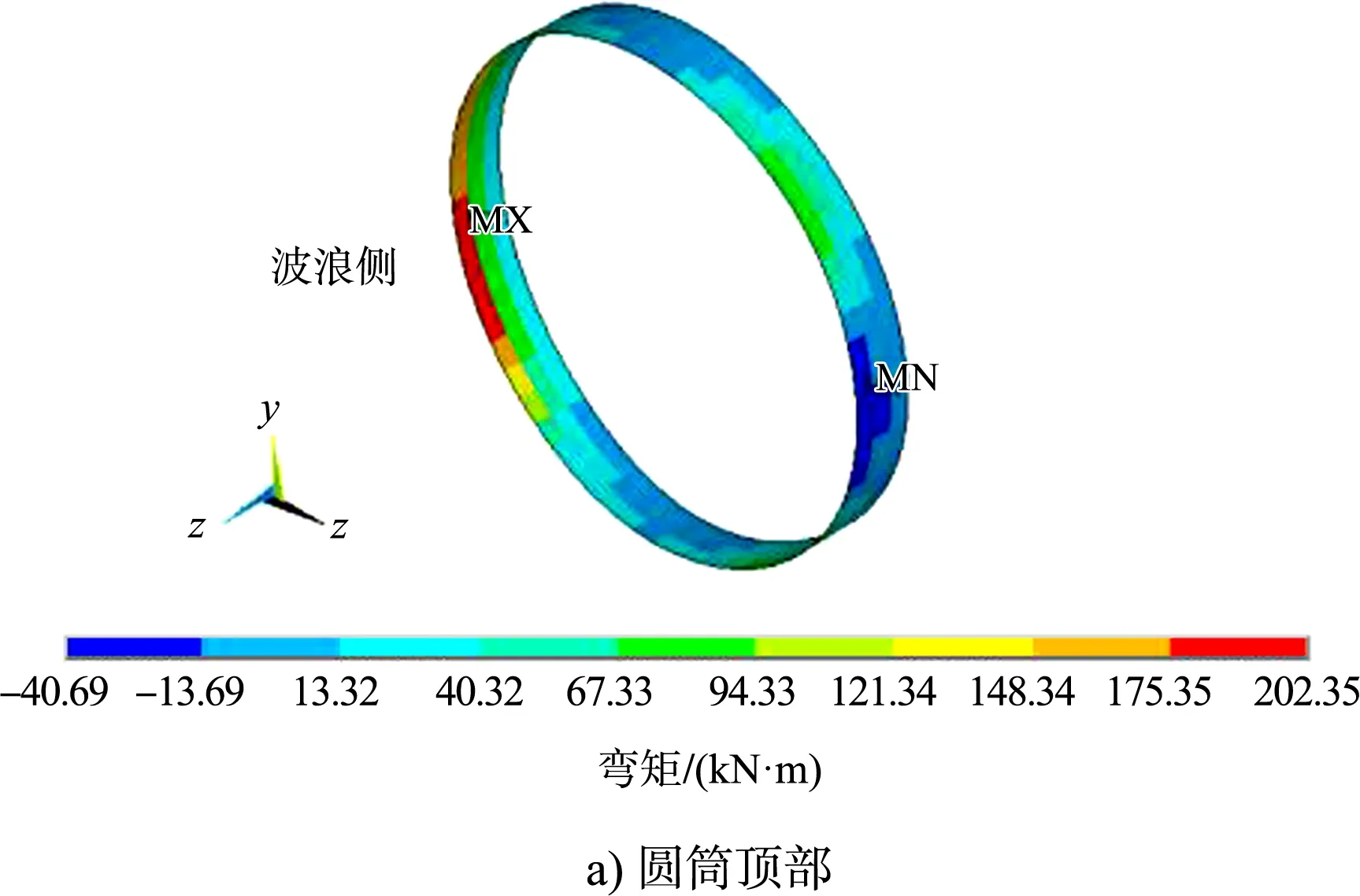
圖6 豎向彎矩分布云圖
結果顯示:頂升荷載作用下,豎向壓力沿圓筒縱向逐漸增大。實際工程中,受重力影響,豎向壓力沿圓筒縱向逐漸增大,說明模擬結果合理。波浪側圓筒頂部出現(xiàn)最大環(huán)向正彎矩202.4 kN·m,波浪側圓筒外側受拉。圓筒頂部最大豎向正彎矩49.1 kN·m。圓筒下部豎向彎矩和環(huán)向彎矩最大值均出現(xiàn)在筒兩端靠近波浪側,但數(shù)值較頂部小。可見岸橋荷載對圓筒頂部環(huán)向彎矩和豎向彎矩影響顯著。實際情況中,卸荷板搭接在圓筒上,而非模型中約束豎向位移,因此圓筒頂部受力結果應乘以一定的折減系數(shù)。
4.2 波浪力
波浪力作用下的內(nèi)力結果見表3,圓筒環(huán)向彎矩分布云圖見圖7。
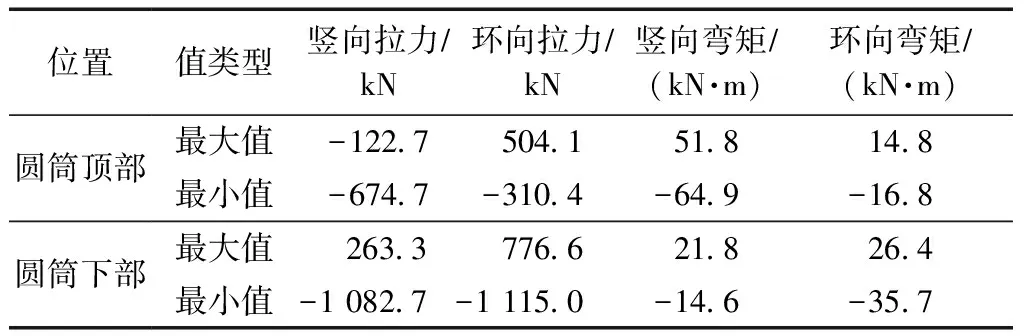
表3 波浪力作用下大圓筒內(nèi)力結果
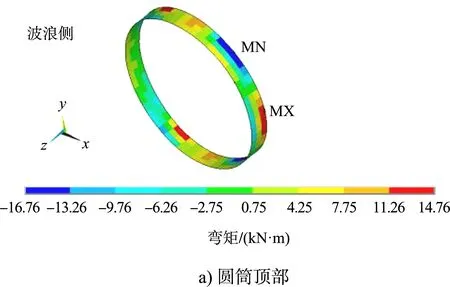
圖7 波浪作用下環(huán)向彎矩分布云圖
結果顯示:波浪作用下,圓筒頂部最大豎向彎矩出現(xiàn)在筒兩端,為51.8 kN·m,環(huán)向彎矩最大值出現(xiàn)在圓筒土側,為14.8 kN·m。圓筒下部最大豎向彎矩出現(xiàn)在筒兩端底部,為21.8 kN·m,最大環(huán)向彎矩出現(xiàn)在筒兩端靠近波浪側,為26.4 kN·m。最小豎向、環(huán)向彎矩均出現(xiàn)在筒兩端靠近土側,分別為-14.6、-35.7 kN·m。圓筒下部整體為波浪側受拉、土側受壓。圓筒頂部環(huán)向彎矩遠小于岸橋荷載作用的結果,下部圓筒內(nèi)力分布與岸橋荷載作用基本一致。
4.3 堆載土壓力
堆載土壓力作用下的圓筒內(nèi)力結果見表4,環(huán)向彎矩分布云圖見圖8。
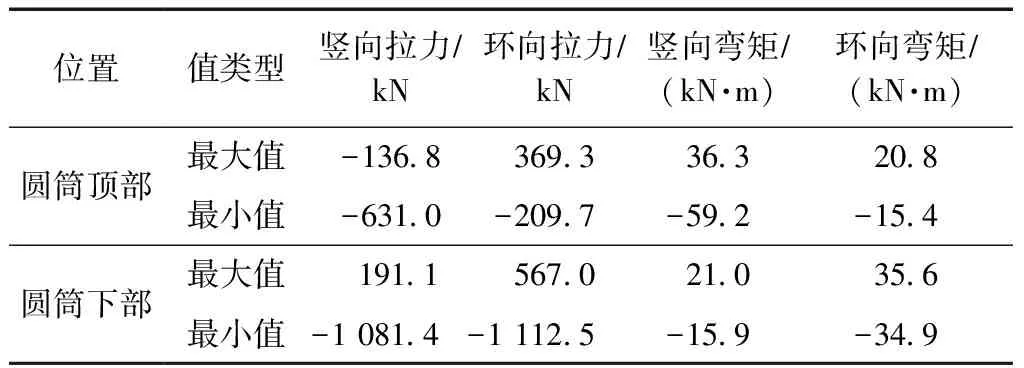
表4 堆載土壓力作用下大圓筒內(nèi)力結果
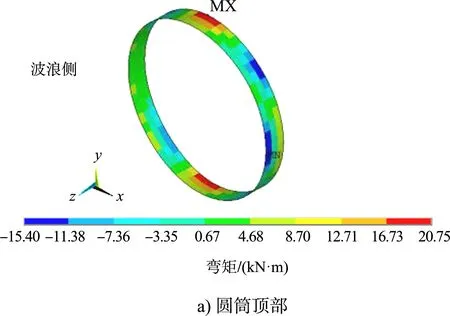
圖8 堆載土壓力作用下環(huán)向彎矩分布云圖
結果顯示:土壓力作用下,圓筒頂部最大豎向彎矩出現(xiàn)在波浪側,為36.3 kN·m,環(huán)向彎矩最大值出現(xiàn)在筒兩端,為20.8 kN·m。下部圓筒最大豎向彎矩出現(xiàn)在筒兩端底部,為21 kN·m,最大環(huán)向彎矩出現(xiàn)在筒兩端靠近波浪側,為35.6 kN·m。最小豎向、環(huán)向彎矩均出現(xiàn)在筒兩端靠近土側,分別為-15.9、-34.9 kN·m,筒壁內(nèi)側受拉。波浪側筒壁受壓,壓力沿圓筒縱向增大,至筒底達到最大值;土側則從筒頂至筒底逐漸由壓力轉為拉力,至筒底達到最大拉力,說明圓筒有向前傾覆趨勢。波浪側環(huán)向拉力沿筒壁縱向增大,土側則從筒底逐漸由拉力轉為壓力,最大環(huán)向拉力為567 kN。
綜上,在3種荷載分別作用下,圓筒下部均為波浪側圓筒壁環(huán)向受拉、土側圓筒壁環(huán)向受壓;波浪側圓筒壁豎向受壓、土側圓筒壁豎向受拉。
5 結論
1)本文通過有限元軟件建立了帶有卸荷板的大圓筒結構三維有限元模型,研究岸橋荷載、波浪力、堆載土壓力分別作用下的結構受力特性。結果表明,在岸橋荷載作用中,頂升荷載為最大荷載。
2)頂升荷載作用下,圓筒頂部豎向、環(huán)向彎矩顯著,分別為202、49 kN·m。而對圓筒下部結構影響與波浪荷載、土壓力大致相同。因此在頂部圓筒處需要增大壁厚并加強配筋,以抵御結構內(nèi)力。
3)受上部結構及荷載影響,圓筒頂部出現(xiàn)豎向彎矩較大值,而圓筒下部受到的環(huán)向彎矩影響更大。圓筒下部整體呈現(xiàn)波浪側受拉、土側受壓的趨勢。
4)針對老舊碼頭改造工程,運用有限元軟件建立帶卸荷板的大圓筒結構整體模型,可綜合考慮上部結構及其荷載,從而得到較為全面的內(nèi)力計算結果,為工程設計提供參考。

