基于原位試驗的砂土地震液化判別方法對比分析
張 林
(大連理工大學土木建筑設計研究院有限公司,遼寧 大連 116023)
在地震地面運動過程中,飽和砂性土孔隙水壓力增加引起的抗剪強度或剛度降低引起明顯的永久性位移,甚至使土的有效應力近于零,應看作是液化。從20世紀60年代開始,人們致力于用系統性的工程方法對這一現象進行評價,現行的土壤液化判別方法比預測液化后果的方法更為成熟[1]。國內外關于液化判別的方法多使用原位試驗進行計算。
用于判別土壤液化的原位試驗有標準貫入錘擊數試驗(SPT)、靜力觸探試驗(CPT)、剪切波速度試驗(vs)、貝克貫入試驗(BPT)及動力觸探試驗(DPT)等,這幾種方法已被國內外學者普遍用于評價地震液化判別。不同的原位試驗適用于不同的地質條件及土壤類型,對于非礫石土壤主要通過SPT、CPT、vs進行液化判別[2],其判別公式有廣泛的數據支撐和豐富的經驗;BPT、DPT可用于礫性土液化判別,在土壤液化評價中的使用頻率遠低于SPT和CPT。
根據歐洲規范,針對液化可能性的評價至少應包括現場標準貫入錘擊數試驗(SPT)或靜力觸探試驗(CPT)及實驗室內測定土顆粒粒徑分布曲線。本文主要對比分析國內外規范利用SPT及CPT的液化判別計算公式,為相關海外工程提供借鑒。
1 國內規范
我國規范中判別液化公式主要是根據SPT來計算,較少使用CPT。SPT操作簡單且與土壤液化性質之間的數據較CPT更為豐富,應用廣泛;而CPT數據連續、誤差小。目前國內外采用的判別公式都是經驗方法,均存在自身的局限性。因此在進行土壤液化判別時,采用多種計算方法綜合判別,有利于深層次理解地震液化,并采取相應的抗震措施,減少地震液化對工程產生的危害。
1.1 標準貫入錘擊數試驗(SPT)
《建筑抗震設計規范》[3]首先根據地震烈度、地質年代、粉土的黏粒含量、上覆非液化土層厚度和地下水位深度之間的關系初步判斷是否需要進行液化判別。若需判別,在地面下20 m深度范圍內,應根據下式進行計算:
(1)
式中:Ncr為液化判別標準貫入錘擊數臨界值;N0為液化判別標準貫入錘擊數基準值;ds為飽和土標準貫入點深度(m);dw為地下水位(m);ρc為黏粒含量百分率,當小于3%或為砂土時,應采用3%;β為調整系數。
當飽和土標準貫入錘擊數(未經桿長修正)小于或等于Ncr時,應判為液化土。對存在液化砂土層、粉土層的地基,應探明液化土層的深度和厚度,并計算液化指數評估液化等級,根據液化的嚴重程度采取相應的抗液化措施。
1.2 靜力觸探試驗(CPT)
《巖土工程勘察規范》[4]提供了利用CPT的判別液化的公式,該公式是根據地震不同烈度區的試驗資料,用判別函數法統計分析得出的。當實測計算比貫入阻力Ps或實測計算錐尖阻力qc小于液化臨界值Pscr或qccr時,應判別為液化土。
2 國外判別方法
目前國外判別液化公式主要是基于Seed和Idriss[5]提出的簡化方法。1996年,Youd等[6]專家召集了一個由國家地震工程研究中心(NCEER)主辦的研討會,回顧了過去10年的發展,目的就是更新和完善簡化方法。國內大部分關于地震液化判別的論文亦是使用NCEER推薦的Seed和Idriss方法。Boulanger等[7]對無黏性土的CPT和SPT液化評價方法進行了重新研究,提出了改進方法,該方法也常被一些國外咨工使用。
上述兩種方法計算過程大體一致,主要是一些參數取值不同。計算公式均是根據SPT和CPT數據,計算土層的循環應力比CSR和循環抗力比CRR,當安全系數FS大于1.25[8],則認為土層非液化。
3 NCEER方法
3.1 安全系數FS
(2)
式中:MSF為震級比例因子;Kσ為豎向有效壓力修正系數;CRR7.5為地震震級為7.5 級(矩震級)的循環抗力比;CSR為循環應力比。
最初的震級比例因子是通過將一個給定震級對應的加載循環次數的代表性曲線上的CSR值除以15個加載循環(相當于7.5級地震)得到的。
Idriss等[9]對震級比例因子進行了修訂,由下式計算:
MSF=102.24/M2.56
(3)
式中:M為地震矩震級。
根據公式(3),CSR與導致液化的循環次數之間的代表性關系見圖1。NCEER推薦采用公式(3)計算MSF,但對于震級小于7.5級的情況,公式(3)計算較為保守,NCEER將其作為下限值,上限值則建議采用Andrus[10]的方法。不同研究者定義的比例因子值見表1。
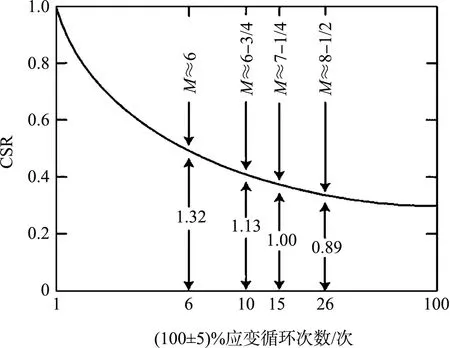
圖1 CSR與導致液化循環次數之間的代表性關系

表1 不同研究者定義的比例因子值
Hynes等[11]編輯和分析了一個擴大的數據庫,為Kσ的取值提供指導和計算公式:
(4)

3.2 循環應力比(CSR)
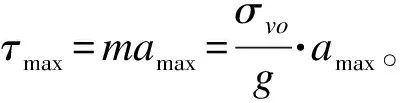
(5)
式中:amax為地震動峰值加速度;σvo為土體計算深度處豎向總應力;g為重力加速度。
隨著深度的增加γd取值范圍變大,根據Liao等[12]公式計算的γd為平均值:
(6)
式中:z為地表以下深度(m)。
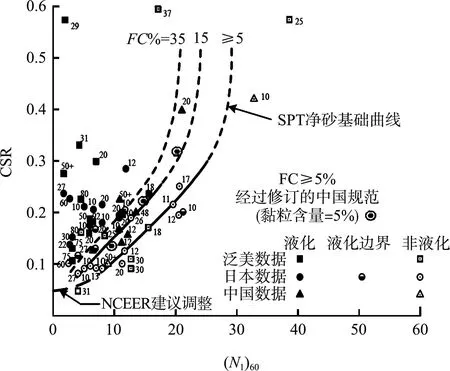
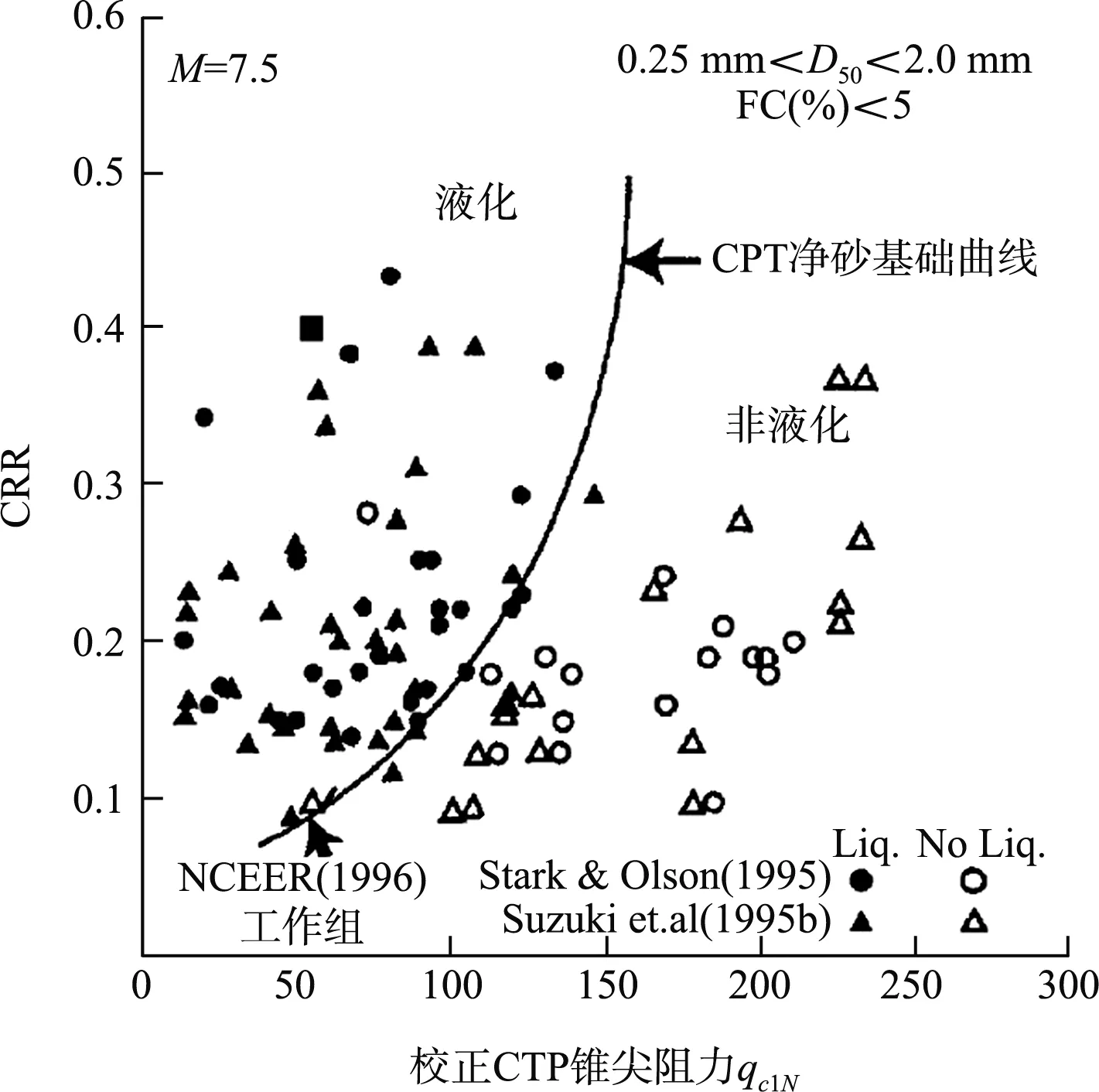
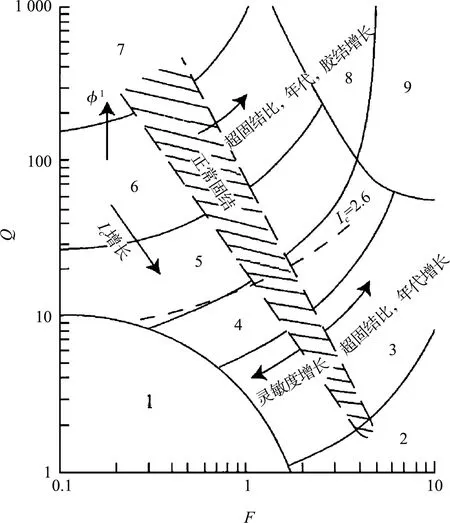
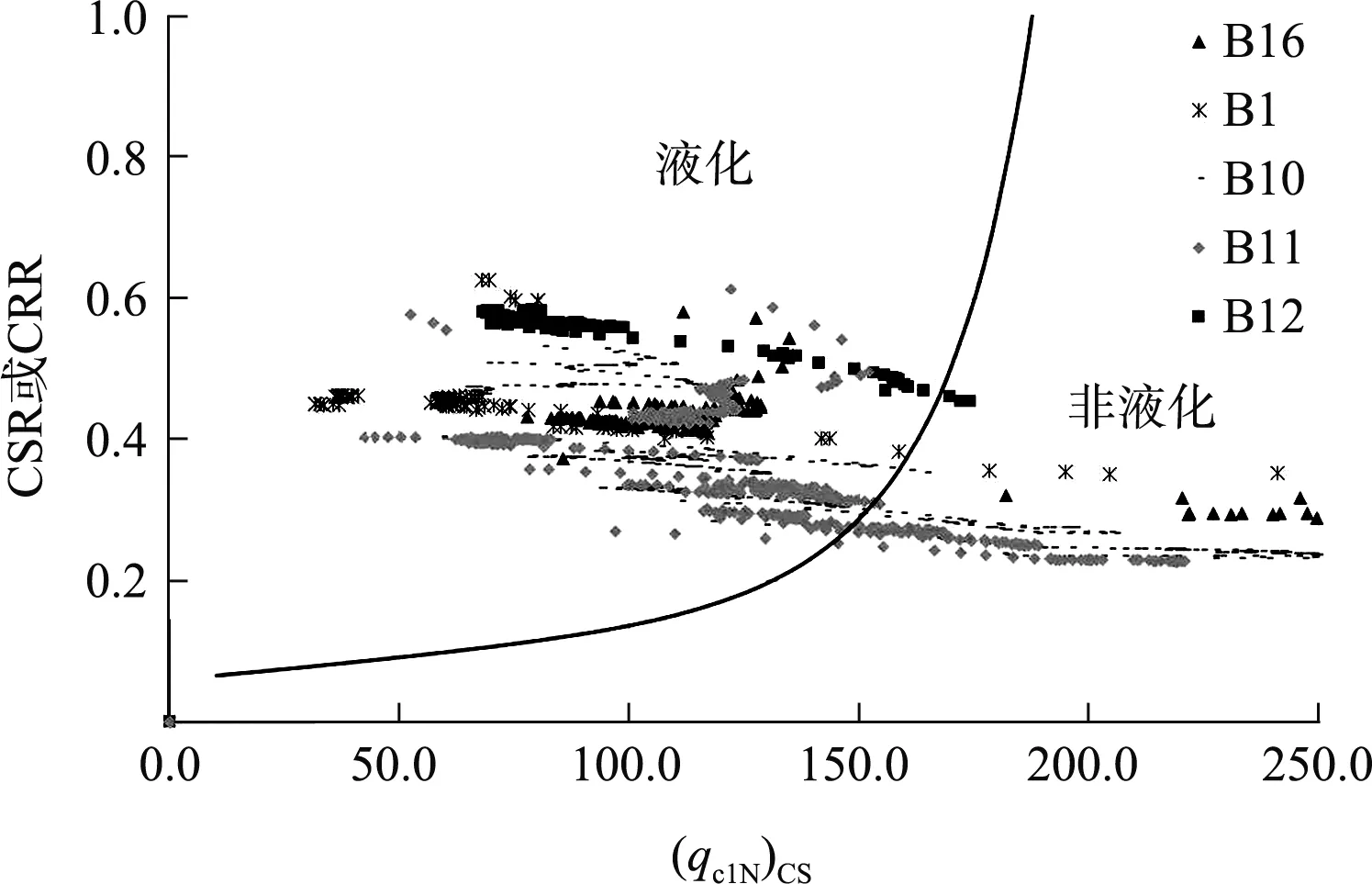
對于z>23 m的情況,國內外學者均給出了相關經驗公式,Robertson等[13]認為γd=0.744-0.008z(23 m 與循環應力比不同,循環抗力比計算是利用歷史上基于原位試驗地震液化數據進行擬合,因此不同學者的擬合公式及計算參數有較大區別。 3.3.1標準貫入錘擊數試驗(SPT) Seed等[14]基于歷史數據繪制的CRR和(N1)60關系曲線見圖2。由圖2可知,隨著細顆粒含量增加,CRR明顯增加。這種增加是否由液化阻力的增加或貫入阻力的減少引起尚不清楚。NCEER在此基礎上,對于較低(N1)60處的曲線彎曲至約0.05。 圖2 基于液化案例歷史數據的7.5級地震SPT凈砂基礎曲線 NCEER推薦采用Rauch的公式(7)擬合圖2的曲線。 (7) 式中:CRR7.5為地震震級為7.5級(矩震級)的循環抗力比;(N1)60為將實測貫入擊數修正為上覆荷載為100 kPa、能效比為60%的標準貫入擊數。 公式(7)適用于(N1)60<30。對于(N1)60≥30,干凈的顆粒狀土壤密度太大,不能液化,被歸類為不可液化。 對于圖2中FC(細粒含量)大于5%的情況,NCEER建議采用下式將(N1)60修正為(N1)60cs,以(N1)60cs代替(N1)60進行公式(7)計算。 (N1)60cs=α+β(N1)60 (8) 式中:α與β為調整參數,根據細粒含量采用分段函數進行計算,當FC≤5%,α=0,β=1;當FC≥35%,α=5,β=1.2;當5% 除了細粒含量會影響(N1)60的結果外,一些儀器參數也會影響到(N1)60取值,(N1)60計算見下式: (N1)60=NmCNCECBCRCS (9) 式中:Nm為實測標準貫入擊數;CN為標準貫入的超荷修正系數;CE為錘擊能量比校正系數(ER);CB為鉆孔直徑修正系數;CR為桿長校正系數;CS為帶襯管或不帶襯管的取樣器的校正系數。 NCEER早前的論文集公布了CN≤2.0,但最新的推薦公式將CN最大值限制在1.7。根據Liao 和Whitman,CN由以下公式計算: (10) Kayen等[15]提出了公式(11)。NCEER認為公式(11)更適合Seed和Idriss等[16]指定的原始曲線。 (11) 這兩個方程都可用于常規工程應用。對于其他修正系數參考文獻[8]。 3.3.2靜力觸探試驗(CPT) Robertson和Wride 根據CPT數據繪制的CRR曲線(FC≤5%)見圖3。雖然個別數據點并沒有在相應曲線一側,但根據研究和驗證,該曲線整體可靠性較高。 圖3 基于CPT數據和歷史經驗液化數據計算CRR的推薦曲線 (12) 式中:(qc1N)cs為純凈砂的歸一化錐尖阻力。當(qc1N)cs大于160,則認為土層非液化。 歸一化錐尖阻力qc1N根據CPT測量的qc計算,并根據土壤類型和深度進行校正。 (qc1N)cs=qc1N·Kc (13) qc1N=Cq(qc/Pa) (14) (15) (16) (17) 式中:Ic為土體類型指標參數;fs為側壁摩阻力;Q為歸一化無因次錐尖阻力;F為歸一化摩擦系數。 基于CPT的(qc1N)cs計算,首先是區分土壤類型,假設n=1,如果Ic>2.6,則將土壤劃分為黏土,并認為其不能液化,計算結束;如果Ic<2.6,那么土壤可能是顆粒狀的,需重新計算。 假設n=0.5,如果Ic<2.6,那么土壤為砂性土,計算結束;如果Ic>2.6,土壤可能是粉質的,也可能是砂性的,需重新計算。 假設n=0.7,得到新的Ic,結束計算。得到n和Ic后,可計算Cq和Kc。Robertson提出的基于CPT的土類型見圖4。 注:1.靈敏細粒土;2.有機土壤-泥炭;3.黏土:粉質黏土-黏土;4.粉土混合物:黏質粉土-粉質黏土;5.砂混合物:粉砂-砂質粉土;6.砂:純凈砂-粉砂;7.礫砂-密實砂;8.非常硬的砂-黏土砂;9.極硬細砂。 Boulanger和Idriss的FS和CSR的計算公式與NCEER相同,但MSF、γd、Kσ取值不同。 (18) NCEER方法MSF僅與震級有關;而Boulanger和Idriss計算的MSF除了與震級有關,還與(qC1N)cs和(N1)60cs有關。當M<7.5,(qC1N)cs≥180或(N1)60cs≥31.5時,Boulanger和Idriss計算的MSF偏小,FS亦偏保守。 應力折減系數由以下公式計算而出: γd=exp[α(z)+β(z)·M] (19) NCEER方法僅考慮了深度的影響,而Boulanger和Idriss考慮了震級的修正,計算更為精確。對于M=7.5的情況,當深度大于9.15 m時,Boulanger和Idriss計算的γd明顯大于NCEER方法,會使CSR偏大、FS偏小。 豎向有效壓力修正系數由以下公式計算得出: (20) 對于CPT試驗, (21) 對于SPT試驗, (22) 通過將(qc1N)cs限制為≤211和(N1)60cs≤37,可以將系數Cσ限制為0.3的最大值。與MSF類似,Boulanger和Idriss方法將(qC1N)cs和(N1)60cs引入到Kσ計算中。 4.2.1標準貫入錘擊數試驗(SPT) (23) (N1)60cs=(N1)60+Δ(N1)60 (24) (25) 式中:Δ(N1)60為根據細顆粒含量的對(N1)60進行的修正值。 (N1)60cs直接利用經驗公式(24)(25)進行計算,FC越小,公式計算的(N1)60cs與NCEER方法計算的結果相差越大。因此根據歐洲規范當深度小于3 m時,(N1)60值應降低25%。經過設備參數修正的(N1)60計算與NCEER相同,見公式(9),但是標準貫入的超荷修正系數CN由公式(26)迭代計算,即m值需要根據(N1)60cs計算,得到CN后,根據公式(9)計算(N1)60,最后迭代得出(N1)60cs。 (26) (27) 4.2.2靜力觸探試驗(CPT) (28) (qC1N)cs計算步驟與(N1)60cs相同,同樣需要根據FC進行修正。 (qC1N)cs=qC1N+ΔqC1N (29) (30) (31) 式中:ΔqC1N為根據細顆粒含量對qC1N進行的修正值;CNe為修正系數,物理意義與公式(26)相同,但m=1.338-0.249(qC1N)cs0.264。 北非某擬建港區大部分處于河口匯水盆地淺灘,原狀地形自南向西北傾斜,水深在0~40 m。根據地勘報告鉆孔揭露,Z系列鉆孔(SPT)主要在淺水區,孔頂高程約為-10 m,巖面較深;B系列鉆孔(CPT)主要集中在深水區,孔頂高程約為-35 m,巖面較淺。 在判別項目范圍內地震液化整體趨勢時,首先對兩個系列鉆孔進行初步判斷,發現兩個系列鉆孔均存在液化土層,見圖5、6。Z系列鉆孔液化土層主要集中在表層和軟弱夾層,B系列鉆孔液化土層分布于鉆孔表層,巖面以上土層基本呈液化狀態。 圖5 Z系列鉆孔液化判別(SPT) 圖6 B系列鉆孔液化判別(CPT) 為了對比兩種國外方法計算的安全系數差異,采用兩個代表性的SPT和CPT鉆孔進行詳細計算,見圖7。在判別是否液化時,兩種方法的結果是一致的。利用SPT鉆孔計算出的安全系數也基本一致。而依據CPT鉆孔判別,雖然均判斷為液化土層,但Boulanger和Idriss方法較為保守。 圖7 不同計算方法液化判別安全系數 研究表明,NCEER 方法對預測液化和非液化的可靠性均在80%以上。而Boulanger和Idriss方法從深度、細顆粒含量、上覆土壓力等方面改進NCEER方法,安全余量較大,但工程實踐較少。 國內規范CPT判別法沒有考慮上覆應力對CPT錐尖阻力的影響,且計算CPT錐尖阻力臨界值偏于保守。SPT判別法沒有考慮到黏粒含量對抗液化強度的影響。因此,國內判別液化方法更為保守。 Boulanger和Idriss方法相較于其他方法,既能滿足安全性又兼顧經濟性。同時,本項目國外咨工亦推薦采用此方法。為了保持一致性,本項目選用Boulanger和Idriss方法對原始鉆孔進行液化判別。并根據碼頭結構類型和地質條件選取無填料振沖方法進行地基處理。 為了滿足結構安全性,在進行地基處理后的土層進行工程驗收時,無填料振沖法效果同樣采用原位試驗來檢驗。使用SPT操作簡單,且與土壤液化性質之間的數據較CPT更為豐富,應用廣泛。而使用CPT錐尖阻力與摩阻比指標可以建立土類分類圖,土體粒組劃分、可塑性都能得到很好的反映。并且,CPT由于數據連續、操作誤差小,近來隨著歷史地震數據的積累,也逐漸成為一種液化判別的常規手段。 1)基于SPT試驗,NCEER 方法和Boulanger和Idriss方法安全系數差別不大;基于CPT試驗,后者較為保守。NCEER方法對預測液化和非液化的可靠性較高,國際認可度較高。而Boulanger方法是在簡化方法和大量研究與經驗的基礎上總結的,既安全又經濟,對國外工程適應性較強。 2)在進行地基處理后的土層進行工程驗收時,使用SPT操作簡單,且與土壤性質之間的數據較CPT更為豐富,應用廣泛。而使用CPT則數據連續、操作誤差小。 3)根據歐洲規范,針對液化可能性的評價至少應包括SPT或CPT及實驗室內測定土顆粒粒徑分布曲線。有條件的情況下,宜采用兩種以上方法進行計算并相互驗證,并建立相關關系,可為相關工程提供借鑒。3.3 循環抗力比(CRR)
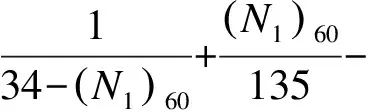
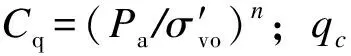
4 Boulanger和Idriss方法
4.1 安全系數FS和循環應力比(CSR)

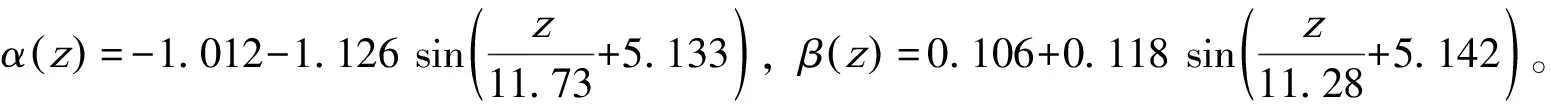
4.2 循環抗力比(CRR)

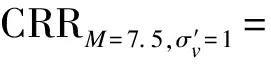
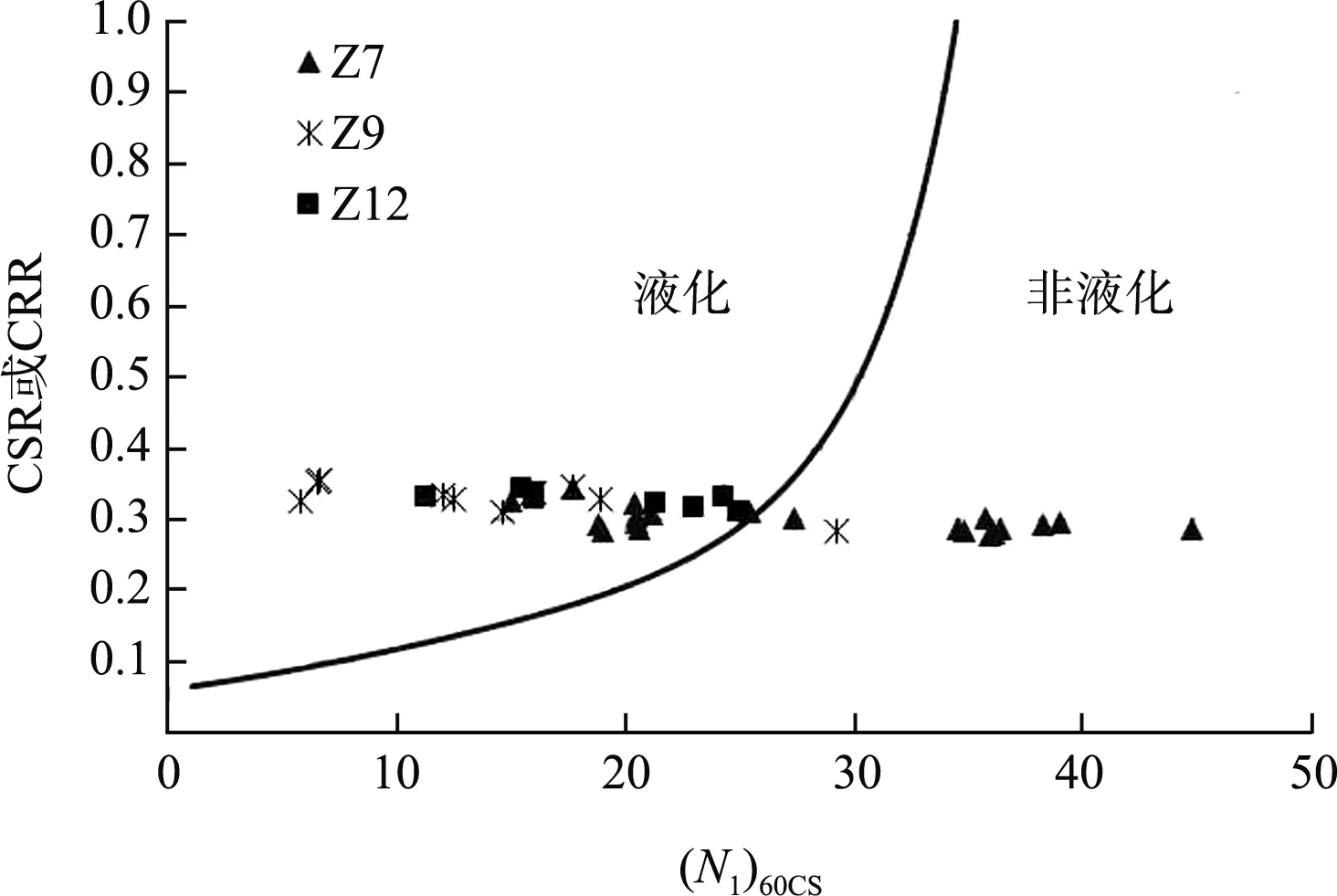
5 對比分析
6 結論

