2MW風電塔筒的力學分析和結構優化

侯夢楠，胥光申，孫戩*,，劉暉，成小樂，王新可

2MW風電塔筒的力學分析和結構優化

侯夢楠1，胥光申1，孫戩*,1，劉暉1，成小樂1，王新可2

（1.西安工程大學 機電工程學院，陜西 西安 710048；2.大唐陜西發電有限公司 灞橋熱電廠，陜西 西安 710065）

針對大型風電塔筒在風輪激勵下容易發生共振、導致塔筒結構受損的問題，結合風力塔筒的結構特點及受力特征進行仿真分析。通過建立有限元模型進行靜力學分析和模態分析，分別確定了塔筒的最大應力、塔頂位移和固有頻率及振型。結果表明：塔筒的應力、位移均符合安全要求，而風輪的激勵頻率和塔筒的固有頻率接近會導致結構發生共振。需對結構進行優化，并通過統計、分析系統各參數對優化目標的敏感度，以及系統輸入參數對優化目標的反應等制定了優化方法，經優化后風電塔筒的固有頻率從0.84039 Hz提高到1.1016 Hz，從而實現了優化目的。

風電塔筒；靜力學分析；模態分析；結構優化

風電作為清潔且可再生資源，具有很好的發展前景[1]。目前，對于風力發電機的研究大部分都集中在風輪葉片、發動機的性能和局部結構方面，而塔筒本身的安全問題具有更為重要的意義[2]。風電塔筒損壞的主要原因是結構振動和長期受力下材料疲勞，因此塔筒的力學分析對于塔筒的安全起著決定性作用[3]。

張曉峰等[4]通過建立風電塔筒三維有限元模型，分析了1.5 MW風電塔筒的靜態強度和剛度，計算出塔筒在不同負載下的應力、塔頂位移，結果表明塔架整體結構滿足強度和剛度要求，為塔筒優化提供了依據。徐奴文等[5]針對經典遺傳算法的不足，提出了一種改進算法的設計模型，分析出風電塔筒在屈曲約束下的最優方法。HongZhu Shan等[6]以55 kW的小功率直驅永磁發電機為例，針對發電機組和對應塔筒發生共振產生的振幅變大問題，采用建立有限元模型進行模態分析的方法，確定模態振型和固有頻率，來接收不同激勵下的塔頂振幅，結果所示與規范相符。葉青等[7]利用Pro/E三維建模軟件構造1.5 MW的風力機傳動系統模型，并在ADAMS中進行力學分析，得到了應力云圖。N. Bazeos等[8]研究風電塔筒靜強度和穩定性，分析了在不同荷載下塔筒的安全運行情況。盧華興等[9]通過研究傳統型、加筋型和混合型三種不同結構的風電塔筒的靜強度性能和模態頻率對比，分析了混合型風電塔筒的應力極值和剛度較其它兩種有所提高，使得結構更加穩定，有利于塔筒剛性模態設計。高俊云等[10]采用應變測試法對于塔筒在不同工種和風速下進行載荷測試，分析了塔筒根部的一階固有頻率，并與仿真計算結果做了對比，表明仿真結果與實測結果接近，模型分析可用與載荷計算和動態性能分析。

對塔筒進行系統的動靜特性分析及結構優化對其安全應用具有現實意義。本文以2MW垂直軸風電塔筒為研究對象，利用SolidWorks建立三維模型，導入ANSYS Workbench進行結構靜力學分析和模態分析，得到風電塔筒的應力云圖、等效應變圖和一階固有頻率云圖，并采用多目標搜索法對風電塔筒模型進行結構優化分析[11]，再從眾多優化參數組合中確定最優組合，提高了風電塔筒的固有頻率，使得其系統更加安全。

1 風電塔筒的計算模型

目前大型風力發電機的塔筒都選擇圓錐形塔柱，從受力特征和幾何結構來看，可以簡化為梁彎曲問題[12]。本次研究某定型2 MW風電塔筒，塔高82.38 m，底端外徑4.56 m、頂端外徑2.70 m，底端壁厚35 mm、頂端壁厚20 mm，材料為Q345鋼，具體參數如表1所示。

塔筒受力如圖1所示，風電塔筒的底座為固定約束，荷載主要為軸向的風輪水平推力F，頂端的輪轂、葉片和機艙總重力1，塔筒的自身重力2，輪轂的扭矩和風壓分布載荷P。通過對風電塔筒的過程分析可知，通常情況下，隨著高度的升高，風速逐漸增大，且主體的截面積較大，所以風載是分析過程需要著重考慮的因素[11]。

（1）風輪的水平推力F為：

式中：為推力系數，一般切入風速處和切出風速初分別取1.0和0.5，根據貝茨公式[13]計算，＝8/9；為空氣密度，取1.293 kg/m3；為風速，定義為22 m/s；為掃風面積，取1700 m2。

計算得F＝4.7284×105N。

（2）輪轂、機艙和葉片的重力1為：

1＝（2）

式中：為輪轂、機艙和葉片的總質量和，取4.0×104kg；為重力加速度，取9.8 m/s2。

計算得1＝3.92×105N。

（3）塔筒的自重2為：

將模型導入ANSYS添加往下的重力加速度，自動識別得到2＝。

（4）輪轂扭矩：

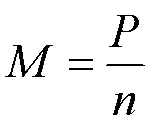
式中：為發電機的輸出功率，W；為風輪的轉速，r/min。

把＝2×106W、＝1/3 r/min代入式（3）可得＝6×106N?m

（5）作用在塔筒上的風壓P為：

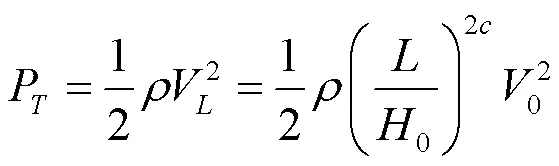
式中：V為高度為處的風速，m/s；為塔筒的高度，m；0＝10 m，即采用10米處的風速轉換；為地面粗糙度和地面風的切變系數，一般取0.156；0為高度10 m處的風速，m/s[14]。

計算得P＝31.2064 N/m。

2 塔筒的靜力分析

在SolidWorks建立風電塔筒的二維模型，以中心軸為旋轉軸得到風電塔筒的三維模型。風電塔筒的整體結構復雜，為了能夠方便準確地分析出其強度及剛度，需要對主體部分進行準備建模。在保證一定計算效率、且對計算結果差別影響不是很大的前提下，省略很多的附屬結構及零部件，以節省節點數量和網格數量。風電塔筒作為主體的分析系統，保留其全部特征，對于塔筒底端僅建立一個節點作為固定約束條件。

將三維模型圖導入ANSYS Workbench中的靜力學分析界面，施加載荷條件和邊界約束，對風電塔筒進行有限元分析，得到等效應力及位移分布如圖2所示，最大等效應力出現在塔筒的底端、為109.81 MPa，最大變形出現在塔筒的頂端邊緣、為0.71703 m。由于結構底端為主體的約束端，所以單向風壓導致越高處結構受彎，自由端位移較大，所造成的變形也達到最大，因此當塔頂的最大位移符合材料變形要求時即塔筒整體的變形符合。

圖2 應力位移云圖

塔筒所受最大應力應小于材料許用應力，根據材料的剛度要求，塔筒的最大變形小于高度的1%[15]，即：

3 塔筒的模態分析

分析模態的固有頻率和模態振型參數的過程為模態分析[16-17]。此次主要分析塔筒的固有頻率，塔筒結構的低階模態對塔筒的穩定性影響相對較大，因此分析塔筒的前六階模態。

由動力學有限元法[18]，可得塔筒系統的動力學方程為：

式中：、、K分別為塔筒的質量矩陣、阻尼矩陣和剛度矩陣；為節點位移；為塔筒受的外力[19]。

表2是模態前六階頻率，圖3為各階模態振型。

表2 前六階模態頻率表

圖3 塔筒的前六階模態

風力發電機風輪額定轉速為18 r/min，可得風輪旋轉頻率為0.3 Hz、葉片通過頻率為＝0.9 Hz，因為(1－)/＝(0.8409－0.9)/0.9＝0.0657＜10%[15]，表明在此頻率激勵下有塔筒發生共振的可能。

4 塔筒結構的優化

由上計算分析可知，風電塔筒的結構容易發生共振而引起結構的破壞、導致塔筒的倒塌，因此需要對塔筒進行結構優化，提高其固有頻率來有效避免結構共振。

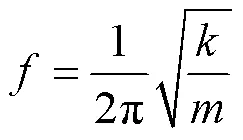
式中：、、分別為剛度、固有頻率和質量[20]。

由式（7）可知，固有頻率的大小取決于模型本身的剛度及質量。對于風電塔筒本身，質量的變化和剛度的改變幾乎是等比的，優化的結果意義不大[21]，因此通過降低塔筒本身的質量是提高固有頻率的有效方法，在考慮安全性的條件下，盡可能地減少模型的質量來避免共振破壞。

優化設計的三要素為設計變量、約束條件和目標函數：風力機的功率、塔筒高度已經確定為不變量，選擇塔筒塔底壁厚、底座長和塔頂壁厚作為設計變量，分別用123表示；優化目標為在保證安全的靜力學強度和較大的固有頻率的條件下[22]取得的最佳尺寸；約束條件為將塔筒的底端完全固定，即約束塔筒底部的六個自由度。

此次優化是一種基于響應面法的多目標搜索優化設計方法，設計搜索的目標有塔筒的最大位移、最大應力和塔筒的一階頻率。首先將SolidWorks中的尺寸進行參數化設置，再將SolidWorks和ANSYS Woekbench進行關聯，使得尺寸參數能夠進行互相識別。在ANSYS Workbench的優化工具Design Exploration中[23]定義輸入參數123的取值范圍，一般為初始值基礎變動上下10%，進而進行敏感性分析，即研究輸入參數對于輸出參數的影響[24-25]，由所得到的輸出參數來判斷各個輸入參數對與其影響程度的重要性，再著重分析研究少量參數對于所需值的重要性。從所有結果中選出最佳的設計點，可以確定不同的優化目標用于優化設計[25]。敏感系數的正負值[27]表示輸出參數對于輸入參數的增減性。該優化的數學模型如圖4所示[28-29]，可以看出：輸入參數1對質量的敏感度最大，系數0.61363，為正向遞增；輸入參數1對應力和應變的敏感度較大，系數分別為-0.45677和-0.41964，為負向增加；輸入參數2對于應力和應變的敏感度最大，系數分別為-0.65493和-0.61592，為負向增加；輸入參數3對應力和應變的敏感度適中，系數分別為14.095和11.987，為正向增加；輸入參數1對一階固有頻率的敏感度最大，系數為0.44861。

在多目標優化問題中，一般情況下各優化目標不能同時達到最優，因此分析得到的結果是一系列的解集，這些解被稱為pareto解[30-31]。以下為選取25組生成應力位移的優化值如表3所示，選取10組為以一階頻率作為優化目標的參數集合如表4所示，可以看出：最大等效應力的取值在106～113.36 MPa之間，最大位移的取值處于740.86～750.15 mm之間，在應力和位移都滿足安全條件的要求下以提升固有頻率的大小作為優化約束，ANSYS Workbench計算得到的最優三組優化點如表5所示。

表3 優化設計表參數1

圖4 各設計參數對目標函數的敏感度圖

表4 優化設計表參數2

表5 優化設計表參數3

根據優化要求，在安全性和經濟性方面，三種方案均達到要求，相比較之下，方案二的底座長2相對適中，塔底壁厚和塔頂半徑更便于制造，且一階固有頻率提高更為明顯，故方案二為最合適優化方案，優化后應力由優化前的109.81 MPa降低到109.20 MPa，而一階頻率由優化前的0.84039 Hz提升到1.1016 Hz、提高了31%，基本達到了優化要求。

5 結論

（1）應用ANSYS對2 MW風力機塔筒進行有限元模型的建立，并通過靜力學、動力學分析得到了塔筒頂端的最大位移、最大應力分別為0.71703 m和109.81 MPa，得到的結果基本滿足安全條件。

（2）通過對風電塔筒的模態分析，得到了塔筒前六階固有頻率，與風輪激勵頻率進行比較，因其一階固有頻率與風輪激勵頻率結果靠近滿足共振條件，故采用多目標優化方法，利用ANSYS Workbench的Design Exploration界面，通過改變塔筒的主要尺寸，提升了塔筒的固有頻率，降低了共振引起的破壞，確保塔筒的安全性和經濟性，也為之后的塔筒研究提供了理論依據。

[1]王建強. 風電新能源發展現狀及技術發展前景研究[J]. 智慧中國，2021（6）：92-93.

[2]魏源. 混合式風力發電機組塔架基本力學性能研究[D]. 福州：福州大學，2016.

[3]王印軍，任勇生，孫丙磊，等. 基于ANSYS的垂直軸風力機塔架的力學分析及結構優化[J]. 山東科技大學學報（自然科學版），2011，30（5）：96-102.

[4]張曉峰，張靜，姚金山. 基于ANSYS Workbench的大型風力發電機組塔架靜態分析[J]. 太陽能，2012（15）：36-39.

[5]徐奴文，李俊杰，王衛爭. 基于遺傳算法的風力機塔架最優化設計方法[J]. 可再生能源，2008（1）：13-16.

[6]Shan H Z，Liu Z H. Modal Analysis of a Wind Turbine Tower Based on the Finite Element Method[J]. Applied Mechanics & Materials，2015（744-746）：179-182.

[7]葉青，薛惠芳. 1.5MW風力發電機行星齒輪機構動力學仿真[J].機械制造，2013，51（6）：17-19.

[8]Bazeos N，Hatzigeorgiou G D，Hondros I D，et al. Static, seismic and stability analyses of a prototype wind turbine steel tower[J]. Engineering Structures，2002，24（8）：1015-1025.

[9]盧華興，陳明陽，劉偉，等. 風電機組混合型塔筒靜強度分析與模態分析[J]. 沈陽工業大學學報，2020，42（2）：155-163.

[10]高俊云，姜宏偉，李超峰，等. 風電機組塔筒載荷的測試與分析[J]. 機械設計，2018，35（11）：53-56.

[11]柳勝舉，趙春雨，鄒荔兵，等. 基于ANSYS的風電機組主機吊具強度分析及優化設計[J]. 機械，2021，48（8）：59-64.

[12]李昕濤. 中厚板多輥矯直機結構力學理論分析[J]. 鍛壓技術，2020，45（11）：134-142.

[13]單蕾. 風力機塔架結構選型與性能研究[D]. 哈爾濱：哈爾濱工業大學，2009.

[14]張玉良，程兆雪，楊從新，等. 風力機風輪設計中風速的處理[J]. 沈陽工業大學學報，2006，28（6）：687-689.

[15]宋曦，戴建鑫. 水平軸風力機塔架的力學建模及ANSYS仿真分析[J]. 甘肅科學學報，2011，23（1）：91-95.

[16]王豐華，楊毅，何苗忠，等. 應用有限元法分析變壓器繞組固有振動特性[J]. 電機與控制學報，2018，22（4）：51-57.

[17]馬劍龍，汪建文，董波，等. 風力機風輪低頻振動特性的實驗模態研究[J]. 振動與沖擊，2013，32（16）：164-170.

[18]楊思慧，陳建魁，尹周平. 機架固有頻率優化的結構設計[J]. 機械設計與制造，2018（10）：71-73，77.

[19]李靜平，徐龍河. 鋼及預應力鋼筋混凝土風電塔筒模態分析[J]. 風機技術，2012（5）：58-63.

[20]黃俊明，周孔亢，徐興，等. 空氣懸架固有頻率試驗研究及理論分析[J]. 機械工程學報，2011，47（14）：114-120.

[21]Menet J L. A double-step Savonius rotor for local production of electricity： a design study[J]. Renewable Energy，2004，29（11）：1843-1862.

[22]田永軍，孫爽，張翔宇，等. 金剛石圓鋸片振動與噪聲機理及其減振降噪技術研究綜述[J]. 機械設計，2020，37（3）：1-13.

[23]劉承杰，羅鵬，趙磊，等. 基于ANSYS Workbench曲柄銷軸的優化設計[J]. 應用力學學報，2017，34（6）：1140-1144，1223.

[24]吳立峰，張富倉，范軍亮，等. 不同灌水水平下CROPGRO棉花模型敏感性和不確定性分析[J]. 農業工程學報，2015，31（15）：55-64.

[25]宋明丹，馮浩，李正鵬，等. 基于Morris和EFAST的CERES-Wheat模型敏感性分析[J]. 農業機械學報，2014，45（10）：124-131，166.

[26]姚道壯，楊建國，呂志軍. 基于ANSYS Workbench的貨架立柱截面優化設計[J]. 東華大學學報（自然科學版），2011（4）：438-441.

[27]富坤，富成科，汪友華，等. 基于支持向量機對種群特征回歸分析的自適應遺傳算法[J]. 南昌大學學報（理科版），2007（4）：391-395.

[28]劉瑞萍，張書豪，徐鑫，等. 基于靈敏度分析法的鋁合金人行天橋優化設計[J]. 鋁加工，2021（4）：44-47.

[29]郝偉，徐宏海. 高速動車組驅動齒輪箱的約束模態分析與結構改進[J]. 機械傳動，2021，45（6）：153-158.

[30]姜衡，管貽生，邱志成，等. 基于響應面法的立式加工中心動靜態多目標優化[J]. 機械工程學報，2011，47（11）：125-133.

[31]魏心友，曾國輝，王衛軍. 基于ABAQUS及modeFRONTIER的多目標優化方法[J]. 輕工機械，2016，34（1）：59-63.

Mechanical Analysis and Structure Optimization of 2MW Wind Power Tower

HOU Mengnan1，XU Guangshen1，SUN Jian1，LIU Hui1，CHENG Xiaole1，WANG Xinke2

(1.Collegeof Mechanical and Electrical Engineering, Xi'an Polytechnic University,Xi'an710048,China; 2.Baqiao Thermal Power Plant, Datang Shaanxi Power Generation Co., Ltd., Xi'an 710065,China)

Aiming at the problem that large-scale wind power towers are prone to resonate under the excitation of wind wheels which results in the damage to the tower structure, simulation analysis is carried out based on the structural characteristics and force characteristics of the wind tower. By establishing a finite element model for static analysis and modal analysis, the maximum stress, top displacement, natural frequency and mode shape of the tower are determined. The results show that the stress and displacement of the tower meet the safety requirements, and when the excitation frequency of the wind wheels and the natural frequency of the tower are close, the resonance of the structure occurs. The structure needs to be optimized, and the optimization method is formulated through statistics and analysis of the sensitivity of the system parameters to the optimization target, and the response of the system input parameters to the optimization target. The result shows that the natural frequency of the wind turbine tower after optimization is increased from 0.84039 Hz to 1.1016 Hz, thus the optimization is achieved.

wind power tower；statics analysis；modal analysis；structure optimization

TH112

A

10.3969/j.issn.1006-0316.2022.03.010

1006-0316 (2022) 03-0058-07

2021-11-10

陜西省重點研發計劃（2018GY-130，2019GY-119）；西安市現代智能紡織裝備重點實驗室（2019220614SYS021CG043）；陜西省教育廳服務地方專項計劃（19JC019）

侯夢楠（1996－），男，陜西渭南人，碩士研究生，主要研究方向為風電塔筒。*通訊作者：孫戩（1985－），男，陜西安康人，博士，講師，主要研究方向為紡織機械設計與優化、復合材料力學、材料成型，E-mail：sunjian@xpu.edu.cn。