支氣管肺泡灌洗結合糖皮質激素治療急性加重期特發性肺纖維化患者的效果及安全性

張萌 李威 徐敬敬

駐馬店市中心醫院RICU，駐馬店 463000

特發性肺纖維化（IPF）為一種以慢性、進展性纖維化病變為主要特征的肺間質疾病，多見于40歲以上中年男性群體。目前，臨床尚未明確此病發病原因，但考慮與肺泡上皮細胞凋亡、成纖維細胞增殖、細胞外基質調節以及抗氧化力失衡等機制密切相關［1］。IPF患者多伴有進行性呼吸困難表現，除典型的乏力、陣發性干咳癥狀外，隨病情進展，患者肺部可逐步出現纖維化病變［2］。此病具有較高致殘、致死風險。現階段，臨床仍缺乏治療IPF的有效手段。以潑尼松片為代表的糖皮質激素類藥物在IPF患者的治療中有廣泛應用。此藥可通過抑制白細胞、巨噬細胞聚集于炎癥部分產生抗炎效果，亦可通過減少T淋巴細胞數而介導免疫球蛋白與表面受體相結合產生的免疫反應［3］。臨床實踐表明，僅依賴糖皮質激素治療IPF的效果并不理想，部分患者治療后預后仍較差［4］。支氣管肺泡灌洗（BAL）為一種用于診斷、治療多種肺部疾病的重要手段，通過纖維支氣管鏡可向支氣管肺泡內注入生理鹽水并吸出，可有效清除肺內病變組織的有害微生物。BAL在慢性阻塞性肺疾病、間質性肺炎甚至肺部惡性腫瘤中均有廣泛應用［5］。為進一步優化IPF患者的治療方案，本研究探討BAL結合糖皮質激素治療急性加重期IPF患者的效果及安全性。

資料與方法

1.一般資料

選取2021年1月至2022年10月至駐馬店市中心醫院收治的123例急性加重期IPF患者進行隨機對照試驗。采用抽簽法將患者分為對照組61例和觀察組62例。對照組男40例，女21例，年齡42～78（60.45±5.25）歲，病程1～5（3.32±0.11）年，吸煙10～30（20.25±5.37）年；觀察組男42例，女20例，年齡40～80（61.25±5.36）歲，病程2～4（3.11±0.45）年，吸煙15～25（21.28±5.44）年。兩組患者一般資料比較，差異均無統計學意義（均P>0.05）。

本研究經駐馬店市中心醫院醫學倫理委員會審核通過（W00213）。

納入標準：⑴入組患者均符合IPF診斷要點［6］，經臨床評估確認病情處于急性加重期；⑵吸煙史均在10年以上；⑶均伴有不同程度的進行性呼吸困難、干咳、杵狀指等癥狀表現；⑷均經影像學檢查確認存在網格影或蜂窩肺；⑸均已知悉此次研究試驗目的及內容，同意且自愿參與研究。

排除標準：⑴已明確病因的間質性肺疾病患者［7］；⑵參與本研究前1個月內接受過其他藥物、非藥物治療者；⑶存在肝腎、心肺功能異常者；⑷存在精神、認知障礙性疾病者；⑸依從性差，不愿配合研究者。

2.方法

2.1.對照組 口服糖皮質激素治療。服藥前先針對癥狀表現予以吸氧、解痙、化痰、抗感染治療。本次研究所用糖皮質激素為潑尼松片（廠家：黑龍江哈星藥業集團有限公司；國藥準字：H23020010；規格：5 mg），每次按0.50 mg/kg劑量口服，1次/d，持續用藥1個月后將服藥劑量減少為0.25 mg（/kg·次），1次/d，治療3個月。

2.2.觀察組 BAL結合糖皮質激素治療。糖皮質激素用藥方法同對照組，BAL方法如下。⑴實施BAL前6.0 h囑患者禁食，術前2.0 h囑患者禁水，術前0.5 h肌內注射0.5 mg阿托品（廠家：安徽長江藥業有限公司；國藥準字：H34021900；規格：1 ml∶0.5 mg）、10.0 mg地西泮（廠家：四川省長征藥業股份有限公司；國藥準字：H51020677；規格：2 ml∶10 mg）預處理；⑵于鼻黏膜、喉表面注入2 ml濃度為2%的利多卡因注射液（廠家：安徽華源醫藥集團股份有限公司；國藥準字：H31021072；規格：5 ml∶0.1 g）進行表面麻醉，連接鼻導管后持續給氧；⑶經口置入纖維支氣管鏡至病變處進行吸痰，后經支氣管鏡引導注入37 ℃的生理鹽水對病變肺組織進行多次沖洗，每次注入20～50 ml生理鹽水，每日重復沖洗4～5次；⑷沖洗完畢后囑患者取側臥位，并再次注入2 ml濃度為2%的利多卡因注射液，每隔1 d灌洗1次，連續治療14 d為1個療程。

3.觀察指標

3.1.肺纖維化癥狀 治療前、治療3、7、14 d后采用肺纖維化Ashcroft評分［8］評估兩組患者肺纖維化癥狀改善情況，量表分值范圍0～8分，評分越高提示肺纖維化癥狀越嚴重。治療前、治療3個月后檢測并對比兩組患者肺纖維化生化指標，包括血紅素氧合酶-1（HO-1）、細胞間黏附分子-1（ICAM-1）、透明質酸（HA）。

3.2.不良事件 統計并對比兩組患者經不同方式治療后不良事件發生情況，主要包括肺動脈高壓、肺氣腫、胃食管反流（GERD）和阻塞性睡眠呼吸暫停綜合征（OSAS）。

3.3.治療相關并發癥 統計并對比兩組患者與治療相關并發癥的發生情況，主要包括消化道反應、繼發感染、出血、喉水腫等。

4.統計學方法

數據均采用軟件SPSS 22.0處理，計數資料以例（%）表示，采用χ2檢驗，符合正態分布的計量資料以（）表示，采用獨立樣本t檢驗，P<0.05為差異有統計學意義。

結果

1.兩組患者肺纖維化改善情況比較

1.1.兩組患者治療前后Ashcroft評分比較 治療前，兩組患者Ashcroft評分差異無統計學意義（P>0.05）；觀察組治療3、7、14 d后Ashcroft評分均低于對照組（均P<0.05）。見表1。

表1 兩組急性加重期特發性肺纖維化患者治療前后Ashcroft評分比較（分，）

表1 兩組急性加重期特發性肺纖維化患者治療前后Ashcroft評分比較（分，）

注：對照組糖皮質激素治療，觀察組支氣管肺泡灌洗結合糖皮質激素治療

治療14 d后2.28±0.47 3.31±0.46 12.281<0.001組別觀察組對照組t值P值例數62 61治療前7.14±0.36 7.23±0.52 1.118 0.266治療3 d后4.45±1.22 5.33±1.25 3.951<0.001治療7 d后3.05±0.27 4.24±1.33 6.903<0.001

1.2.兩組患者治療前后肺纖維化指標比較 治療前，兩組患者肺纖維化指標水平差異均無統計學意義（均P>0.05）；治療后，觀察組HO-1、ICAM-1、HA水平均低于對照組（均P<0.05）。見表2。

表2 兩組急性加重期特發性肺纖維化患者治療前后肺纖維化指標比較（）

表2 兩組急性加重期特發性肺纖維化患者治療前后肺纖維化指標比較（）

注：對照組糖皮質激素治療，觀察組支氣管肺泡灌洗結合糖皮質激素治療。HO-1為血紅素氧合酶-1，細ICAM-1為胞間黏附分子-1，HA為透明質酸

治療3個月后9.25±2.36 12.75±3.44 6.589<0.001組別觀察組對照組t值P值例數62 61 HO-1（ng/L）治療前80.33±5.27 81.44±5.36 1.158 0.249治療3個月后45.25±10.37 51.72±10.36 3.461<0.001 ICAM-1（ng/L）治療前105.44±10.36 106.33±10.46 0.474 0.636治療3個月后64.48±10.45 70.44±10.28 3.188 0.002 HA（μg/L）治療前30.47±5.28 31.44±5.36 1.011 0.314

2.兩組患者不良事件發生情況比較

治療后，觀察組不良事件發生率低于對照組（P<0.05），見表3。

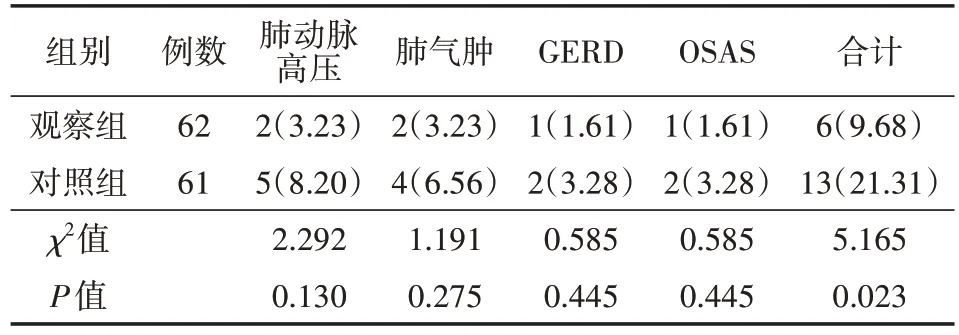
表3 兩組急性加重期特發性肺纖維化患者治療后不良事件發生情況比較[例（%）]

3.兩組患者治療相關并發癥發生情況比較

治療后，觀察組治療相關并發癥發生率略高于對照組（P>0.05），見表4。

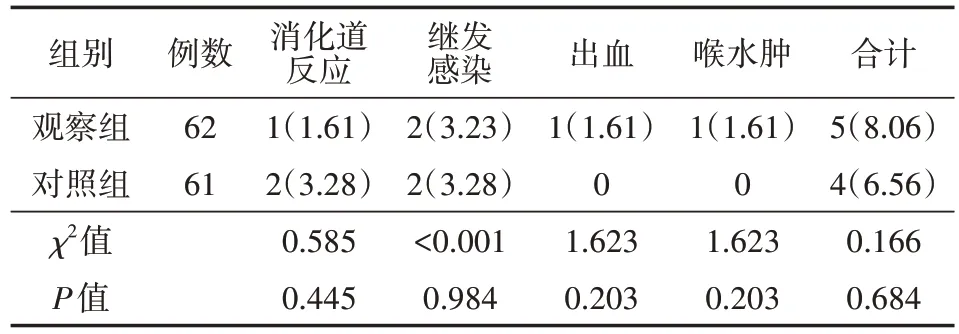
表4 兩組急性加重期特發性肺纖維化患者治療相關并發癥發生情況比較[例（%）]

討論

目前，臨床尚未明確IPF具體發病原因，但考慮與肺泡上皮組織損傷、成纖維細胞形成、細胞外基質在肺泡內過度沉積等因素相關；除漸進性呼吸困難、陣發性干咳癥狀外，隨病情進展，IPF患者的肺功能還可逐步發生退行性病變［9-10］。臨床針對IPF患者多會采用以潑尼松為代表的糖皮質激素進行治療，但對于病情處于急性加重期的IPF患者來說，因其病情進展較快、臨床癥狀更為嚴重，單獨采用糖皮質激素治療的效果并不理想，且長期應用此藥所引發的多種不良反應亦可對患者預后產生不利影響［11］。

BAL為目前臨床用于診斷、治療多種肺部疾病的重要手段；在纖維支氣管鏡輔助下，醫生可通過向肺泡內灌注生理鹽水而對病變組織起到消炎、抗菌功效，將灌洗液集中收集后進行細菌培養也可對其病變、感染類型進行有效鑒別，對指導后續治療方案有重要意義［12］。本研究結果顯示，觀察組治療3、7、14 d后Ashcroft評分均低于對照組（均P<0.05），提示與單獨采用糖皮質激素治療相比，應用BAL配合治療可增加患者臨床獲益。通過向肺泡內注入恒溫生理鹽水并進行反復沖洗后，可幫助排出肺泡內的異物、炎癥產物及免疫代謝產物，對改善肺部炎癥、抑制肺纖維進程均有積極意義［13］。本研究中，觀察組經BAL配合糖皮質激素治療后HO-1、ICAM-1、HA水平均低于對照組（均P<0.05）。相關生物學效應研究表明，HO-1具有一定抗氧化、抗炎機制，作為一種氧化應激蛋白，其表達水平可在肺部出現氧化損傷、纖維化病變時顯著上升［14］。ICAM-1可介導細胞外基質與細胞間的相互作用，可通過介導中性粒細胞到達肺泡腔而加劇肺纖維化進程；而HA也被證實與肺纖維化病程呈顯著正相關［15-16］。IPF為一種可嚴重威脅患者生命健康的肺間質疾病。相關研究數據表明，急性加重期IPF患者中位總生存期僅為2.5～3.5年［17］。此類患者5年內生存率不超過50%。若未及時積極治療，隨病情進展患者可逐步出現肺動脈高壓、肺氣腫、GERD、OSAS等嚴重并發癥，以上并發癥也是導致IPF患者死亡的主要原因［18］。本研究中，觀察組治療后不良事件發生率低于對照組（P<0.05），提示BAL聯合糖皮質激素治療在改善患者遠期預后方面更具優勢。本研究中，觀察組治療相關并發癥發生率略高于對照組（P>0.05），部分患者或因BAL治療期間操作不當而繼發感染、出血、喉水腫等情況，但兩組發生率無明顯差異，提示此治療方法的安全性尚可，可進一步推廣應用。

綜上所述，BAL結合糖皮質激素治療急性加重期IPF患者可有效抑制患者肺纖維化病情進展，對降低不良預后發生風險有重要意義。

利益沖突所有作者均聲明不存在利益沖突

作者貢獻聲明張萌：醞釀和設計試驗，實施研究，采集數據，分析/解釋數據，起草文章，統計分析；李威：對文章的知識性內容作批評性審閱，統計分析；徐敬敬：對文章的知識性內容作批評性審閱，指導