基于懲罰絕對偏差的函數型部分線性模型穩健變量選擇

吳 昊，趙培信*,2，黃海霞

(1.重慶工商大學 數學與統計學院；2.經濟社會應用統計重慶市重點實驗室，重慶 南岸 400067)

0 引 言

隨著科學技術的發展和數據采集技術的提高，在生物醫學、環境工程等領域常常出現以函數曲線形式的函數型數據.關于函數型數據的統計推斷越來越受到關注，并且已有大量文獻進行研究.Yao等[1]研究了函數型線性模型的估計方法，Müller和Stadtmüller[2]研究了函數型廣義線性模型的估計問題，Sentürk和Müller[3]研究了函數型變系數模型的估計問題.關于函數型部分線性模型的統計推斷問題，Shin[4]對模型的參數提出了一種估計方法，Lu等[5]則推廣了文獻[4]的估計方法，并提出了一種分位數回歸方法.另外，Kong等[6]則利用懲罰最小二乘方法研究了函數型部分線性模型的變量選擇問題.

注意到在統計建模過程中，如果忽略某些重要變量或者引入過多的冗余變量都會導致估計和預測的精度下降，因此變量選擇問題是統計建模過程的一個重要組成部分.盡管Kong等[6]研究了函數型部分線性模型的變量選擇問題，但其所用的懲罰最小二乘方法對異常點較敏感，各別異常值則會帶來較大的估計偏差，從而影響變量選擇的精度.為此，本文對函數型部分線性模型的變量選擇問題，提出了一種基于懲罰絕對偏差的變量選擇方法，并且模擬結果表明該方法具有較好的穩健性.

1 基于懲罰絕對偏差的變量選擇過程

記X(t)為來自半度量函數型空間(H,d)的函數型協變量，Z=(Z1,…,Zp)T為來自p維歐氏空間Rp的p維協變量，Y為對應的響應變量，那么函數型部分線性模型具有如下結構：

(1)

其中β=(β1,...,βp)T為未知參數向量，m(·)表示H→R的一個光滑算子，ε為模型誤差，且滿足E(ε|Z,X(t))=0.對模型(1)兩邊在給定X(t)的條件下取條件期望得:

E(Y|X(t))=E(Z|X(t))Tβ+m(X(t))

(2)

結合(1)和(2)式可得

Y-E(Y|X(t))=(Z-E(Z|X(t)))Tβ+ε

(3)

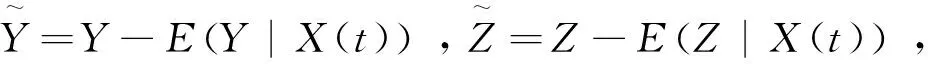
(4)

其中K(·)是核函數，h是帶寬，d(·,·)表示半度量空間?上的半度量距離.進而E(Y|X(t))和E(Z|X(t))的非參數核估計可定義為

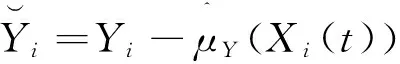
(5)

(6)

注意到目標函數Q(β)關于β在0點不可導，經典的梯度方法不能用于目標函數Q(β)的求解.為此，接下來我們討論最小化目標函數Q(β)的計算方法.結合Zou和Li[10]提出的線性逼近方法，(6)式中的懲罰函數pλ(|βk|)可以漸近表示為

(7)

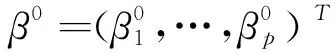
(8)

其中ξk=(0,…,1,…0)T為第k個元素為1，其他元素均為0的p維單位向量.那么(8)式可寫為

(9)

注意到(9)式為經典的最小一乘估計目標函數，因此可以通過已有的統計軟件(如R軟件、SPSS軟件等)進行求解.另外在求解(9)式的過程中，調整參數λ需要指定，并且參數向量β需要給出一個初始估計.首先我們可以通過最小化如下不帶懲罰項的絕對偏差目標函數來得到β的一個初始估計

(10)

另外類似Wang等[11]，本文通過最小化如下BIC準則函數來得到λ的估計.

2 數值模擬研究

為實施模擬，我們從如下模型產生數據

(11)

其中β=(2,1,0.5,0,…,0)T為10維參數向量，對應的協變量Zk～N(1,1.5)，k=1,…,10.由β的前三個元素非零，其他元素均為零可知Z1,Z2和Z3為三個重要的協變量，而Z4,…,Z10均為不重要的協變量.非參數算子m(x(t))取為

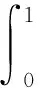
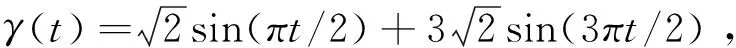
關于重要協變量的變量選擇模擬結果見表1和表2，其中“C”表示基于1000次重復實驗把真實不重要協變量正確估計為不重要協變變量的平均個數，“I”表示基于1000次重復實驗把真正重要協變變量錯誤估計為不重要協變量的平均個數.另外，表1和表2還給出了選擇重要協變量的錯誤選擇率(FSR)，其定義為FSR=IN/TN，其中IN表示基于1000次重復實驗把不重要協變量估計為重要協變量的平均個數，TN表示基于1000次重復實驗所有選擇為重要協變量的平均個數.由表1和表2，我們可以得到如下結論：

(1)隨著樣本量n的增加，基于三種懲罰方法的重要協變量錯誤識別率均逐漸趨于0，并且對不重要協變量的識別也逐漸趨于不重要協變量的實際個數7.這表明本文提出的重要協變量的選擇方法是行之有效的.

(2)對任意給定的樣本量n，在不同異常值數量下的模擬結果是類似的，即異常值對模擬結果沒有明顯的影響.這表明本文提出的變量選擇方法具有較好的穩健性.

(3)當樣本量較小時，基于Adaptive- Lasso和SCAD給出的模擬結果優于基于Lasso給出的模擬結果.但當樣本量增大時，基于三種懲罰方法給出的模擬結果是類似的.

表1 異常值占5%時，基于不同懲罰函數的變量選擇模擬結果

表2 異常值占10%時，基于不同懲罰函數的變量選擇模擬結果

接下來我們給出關于模型參數β估計精度的模擬結果.注意到在任意給定的樣本量下，基于不同的懲罰函數識別重要協變量的模擬結果是類似的.因此在接下來的模擬過程中，我們用Lasso懲罰選擇重要協變量.另外作為比較，我們還給出了關于β的懲罰最小二乘估計模擬結果，即通過最小化如下帶懲罰項的最小二乘目標函數QLS(β)來得到β的估計.

圖1 異常值占5%時，模型參數β估計量GMSE的箱線圖

基于1000次重復實驗，圖1和圖2給出了GMSE在各種樣本量情況下的箱線圖(Box-plot)，其中LAD表示本文提出的基于懲罰絕對偏差估計方法所給出的模擬結果，LS表示基于懲罰最小二乘估計方法所給出的模擬結果.由圖1和圖2可以看出，隨著樣本量的增加，基于本文提出的方法所給出的GMSE逐漸減小，而基于懲罰最小二乘估計方法給出的GMSE即使n增加時仍相對較大.這就表明本文提出的懲罰絕對偏差的估計過程可以有效地消除異常點的影響，從而對模型參數的估計具有相對較高的精度.另外，我們還可以看出對任意給定的樣本量n，在不同異常值數量下，基于本文提出方法的模擬結果是類似的.這表明本文提出的估計方法對模型參數的估計具有較好的穩健性.

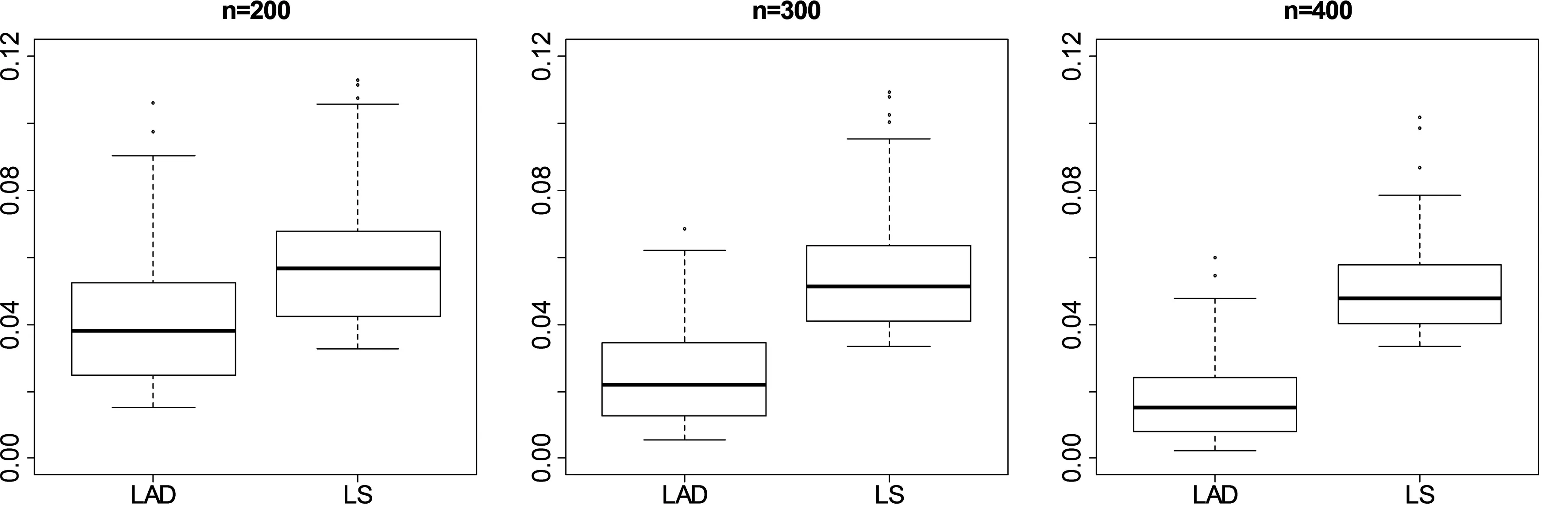
圖2 異常值占10%時，模型參數β估計量GMSE的箱線圖