旋風分離器支撐曲梁設計
萬叢偉 高 玲 陳健陵
(東方電氣集團東方鍋爐股份有限公司,四川 自貢 643001)
1 理論計算
將曲梁簡化為兩跨連續曲線梁,兩端鉸支,中間為豎向鏈桿支座。曲率半徑為4297.5mm,集中力274.4KN。由于鋼梁跨度不大,自重比較小,計算時不考慮自重均布荷載,在驗算時相應的擴大彎矩剪力。
2 曲梁計算
計算簡圖如圖1 所示,梁上共七個集中力,各集中力作用點和O 點連線與OA 夾角分別為13°、21°、28°、36°、43°、51°、58°。
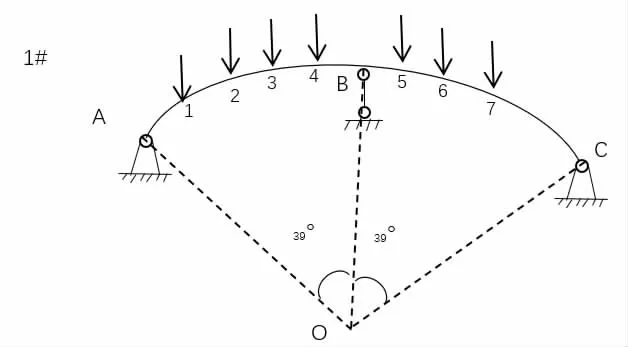
圖1 曲梁計算簡圖
2.1 曲梁截面尺寸確定
鋼結構設計標準GB50017-2017 中6.2.4 節[1],當鋼箱梁滿足:

選取曲梁1#尺寸為:寬350mm,高320mm,壁厚28mm。
2.2 支座B 處負彎矩計算
由我國學者姚玲森所出版的《曲線梁》一書[3],在AB、BC 兩跨上各作用一個集中力時,支座B 處負彎矩為:



圖2 單跨計算簡圖
對于梁1#,兩跨的荷載、曲率和曲率中心角均相等,即 γ=1,并且當第1 跨內有荷載p 作用時,上式(1)可寫成:
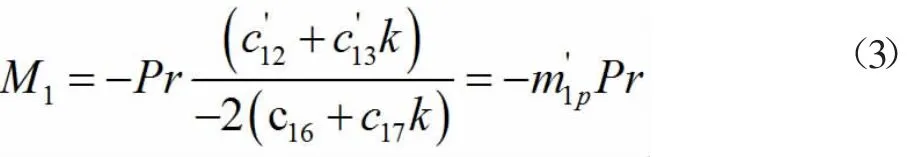
同理,荷載P 作用在第2 跨內時:



表1 各集中力作用下B 支座彎矩
可得B 點彎矩:
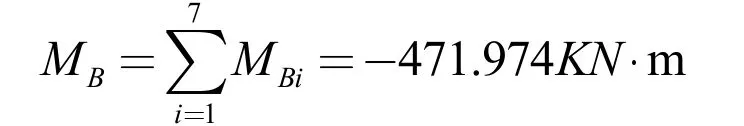

2.3 B 支座處剪力
《曲線梁》書中給出了各截面的剪力影響線。
當荷載P=1 作用于第一跨時:
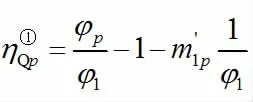
當荷載P=1 作用于第二跨時對于第一跨任意截面的剪力影響線為:

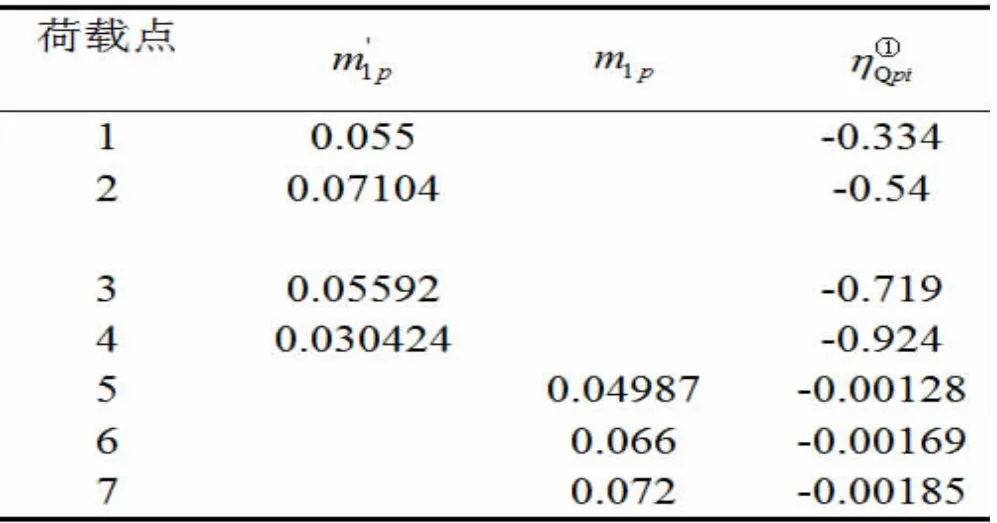
表2 各集中力作用下B 支座剪力
當在有較大彎矩和剪應力同時作用時,構件應滿足:

2.4 AB 跨中處彎矩
《曲線梁》中給出曲線梁上任意截面 φ的彎矩影響線:
2.4.1 當單位荷載作用在第一跨內,且荷載位于計算截面左邊 (≥ φ ≥φ)時:
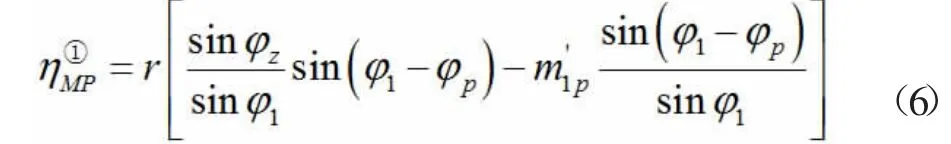
當荷載位于計算截面右邊 (φ ≥ φ≥0)時
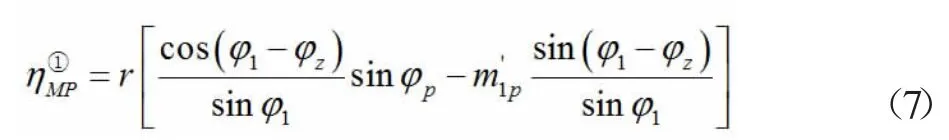
2.4.2 當單位荷載作用在第二跨時:
對于第一跨內任意截面 φz的彎矩影響線:

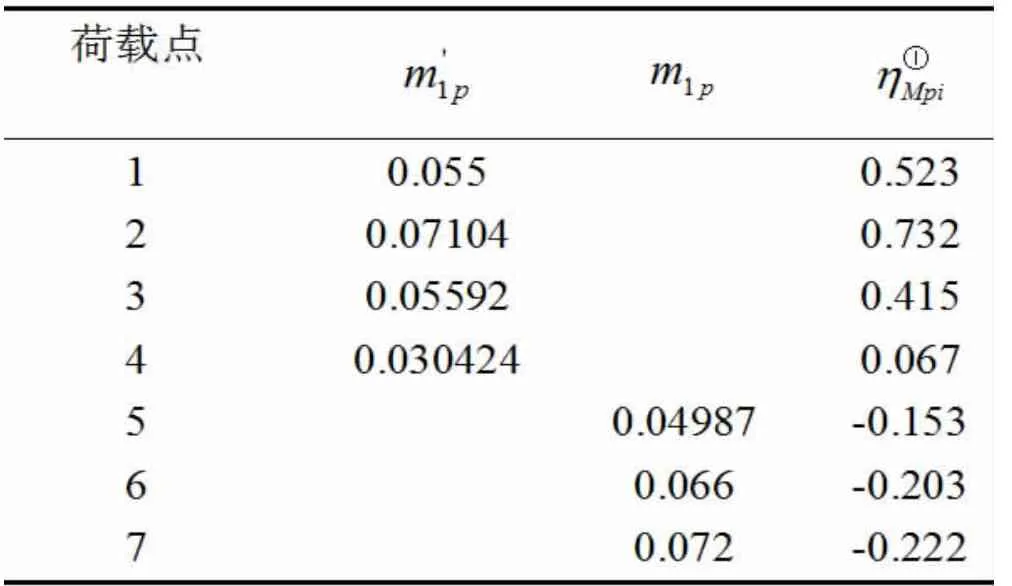
表3 AB 跨中彎矩計算


3 有限元模擬
利用掃掠創建三維實體曲梁部件,長度單位為毫米,隨后創建加筋板、耳板、側向支撐以及支撐梁,這里將下面支撐曲梁只取支撐部位周圍的一段長度,并將支撐梁截斷處的截面固結進行簡化模擬。材料為Q355B,彈性模量密度為7850kg/m3,泊松比為0.3。各部件之間通過綁定相互作用在一起,每個加載點對應位置,在梁內設置12mm 厚加筋板,加筋板上側與上翼板接觸處不綁定。在耳板孔洞處各設置一個參考點,參考點與孔洞耦合后施加集中力 274400× 1 .35 =370440N。設置網格形狀為四面體,劃分網格,見圖3。

圖3 曲梁網格劃分
3.1 曲梁模擬結果
由于在前面理論計算中沒有考慮加筋板、側向支撐等的作用,以及實際工程中支座形式與理論計算中簡化的支座有些差異,因此在有限元模擬結果中,應力最大值以及應力最大位置也發生了一定的改變(見圖4,圖5)。由模擬結果可知,應力最大值為237.5MPa,最大應力位置大致在跨中支座處;最大撓度為1.382mm<L/500=5.85mm,滿足。應力隨時間變化曲線如圖6 和圖7所示。

圖4 曲梁正應力模擬結果
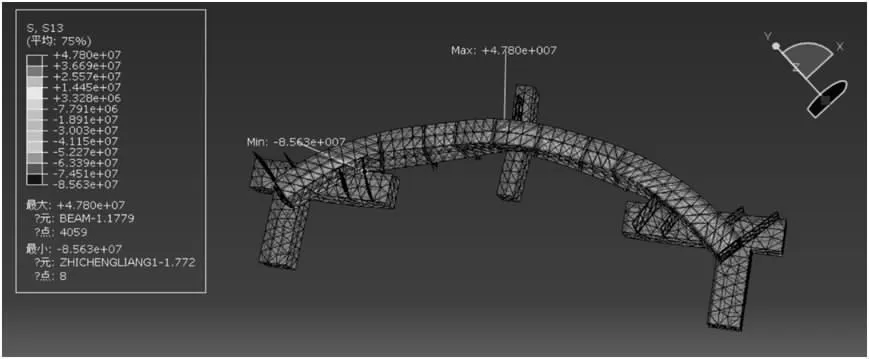
圖5 曲梁剪應力模擬結果

圖6 正應力變化曲線

圖7 剪應力變化曲線
3.2 彈性屈曲分析結果
進行彈性屈曲分析曲梁的臨界荷載,將分析步設置為線性攝動中的屈曲,把各集中力大小改為單位1,模擬結果如圖8 所示。臨界荷載為特征值EigenValue 與單位荷載的乘積,從結果可看出特征值很大,則說明曲梁不會發生彈性失穩。

圖8 曲梁屈曲分析結果
4 與《建筑結構靜力計算實用手冊》計算結果比較
由《建筑結構靜力計算實用手冊》P59 第3 項“對稱集中荷載作用下任意截面的彎矩及扭矩”[4], 可得曲線梁在對稱及反對稱集中荷載作用下任意截面的彎矩以及扭矩。
由于計手冊里的公式只適用于單跨曲線梁,這里將兩跨連續梁1#、2#、3#拆成兩個單跨梁大致計算AB 跨中處彎矩,并與利用《曲線梁》中公式計算得到的AB 跨中彎矩進行比較,比較結果也可以看出兩種方法計算得到的數值相差較多,如表4 所示。其中《曲線梁》所對應的彎矩可通過式(6)、(7)、(8)求得,式中所需參數在前面計算中也都已求出,代入即可。

表4 兩種方法計算AB 跨跨中彎矩

