超高速碎片云撞擊下薄板變形與撕裂建模研究
劉澤榮,龍仁榮,張慶明,陳 利
(北京理工大學爆炸科學與技術國家重點實驗室,北京 100081)
多層板結構廣泛存在于航天器、艦船等結構中[1],然而航天器會遭受在軌超高速空間碎片的撞擊,艦船等目標會遭受超高速動能武器的撞擊[2]。在超高速彈丸撞擊下,多層板結構中的第1 層板形成穿孔,第2 層及其后各層板則承受碎片云的沖擊,即分布式載荷。碎片云的破壞形式與超高速彈丸明顯不同,其破壞特征與尺寸是毀傷評估的重要參數,研究碎片云撞擊下薄板的變形與破壞十分必要。
碎片云碰撞下薄板的變形與破壞可以看作薄板在具有空間分布的瞬態載荷下發生塑性動態大變形問題。薄壁結構是一種常見的結構,薄板變形理論由來已久,其中薄板小變形理論研究相對完善[3],而薄板動態塑性大變形理論仍在發展中。在研究薄板的大變形過程時,一方面需要同時考慮彎矩和膜力的作用,所建模型相對復雜,另一方面其幾何方程具有非線性項,使得位移求解非常困難。Craggs[4]提出用薄膜理論分析薄板大變形,在模型中不考慮彎矩作用而只考慮膜力,這雖然可以簡化理論模型,但是卻只適用于很薄且強度較低的薄板大變形撓曲問題,難以描述常用金屬薄板大變形問題[5]。Reissner[6]首先提出板殼大變形基本理論,隨后Jones[7–8]應用此理論求解了理想剛塑性板在動載荷下的撓曲變形,通過忽略面內變形,從而簡化方程得到理論解。Yu 等[9]引入膜力因子,將膜力對板變形的影響通過膜力因子乘以平衡方程中的彎矩體現出來,由于方程中不包含膜力項,求解薄板撓曲變形方程的難度大大降低。然而,這些模型忽略或簡化了膜力作用,難以實現大變形高精度的計算。
本研究利用二級輕氣炮開展球形彈丸超高速正撞擊多層板實驗,分析總結薄板在碎片云撞擊下的變形與破壞特征,在此基礎上建立考慮彎矩和膜力作用的環板變形模型,將大變形的薄板材料運動分解為橫向的外凸運動和環向的膨脹運動,并結合Grady 破碎理論,建立環向膨脹花瓣撕裂模型。
1 超高速撞擊多層板實驗及結果分析
采用二級輕氣炮將直徑dp=9.13 mm 的LY12 鋁合金球形彈丸加載至速度v0=5 km/s 后撞擊多層板防護結構。多層板防護結構由4 塊尺寸為100 mm×100 mm 的LY12 鋁合金薄板組成,相鄰兩板間距為:S1=17 mm,S2=50 mm,S3=38 mm;第1 層至第4 層板的厚度分別為:hb1=1.0 mm,hb2=2.0 mm,hb3=2.0 mm,hb4=1.5 mm,如圖1 所示。
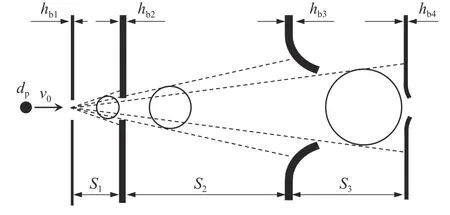
圖1 彈丸超高速碰撞多層板結構Fig. 1 Multi-shock shield structure subjected to hypervelocity impact
實驗后各層板的照片如圖2 所示,第1 層板只發生穿孔破壞,靶板中心有一個規整圓孔。第1 層與第2 層板的間距較小,彈丸與第1 層板碰撞形成的一次碎片云沒能充分膨脹,碎片云載荷依然較為集中,因此第2 層板中央形成了一個大的穿孔,孔四周出現一個由小碎片撞擊形成的環狀小坑區域。第3 層板與第4 層板的破壞特征相似,板中間有穿孔破壞,孔周邊材料發生拉伸完全變形,并且發生撕裂破壞,如圖2(c)、圖2(d)、圖2(e)所示。第3 層板彎曲撕裂至靶板邊界,邊沿夾持的卡具也發生了彎曲大變形。由于第3 層板的阻擋,作用到第4 層板的碎片云能量大幅減小,第4 層板的彎曲變形主要集中在中部區域,邊沿和卡具均沒有明顯的彎曲變形。由于裂紋擴展所需要的能量較小,第4 層板的裂紋依然擴展至靶板邊沿。第4 層板表面覆蓋一層白色物體,彈坑也相對較少,經分析,白色物是熔融鋁冷卻凝固物,熔融態的碎片云對第4 層板的作用更趨于整體作用,而不是大尺寸固態碎片的局部作用。整個多層板結構在超高速彈丸撞擊下的變形特征如圖1 所示。

圖2 高速沖擊后各層板的破壞照片Fig. 2 Damage results of each layer after hypervelocity impact
實驗結果表明,彈丸與集中分布的碎片云撞擊薄板會造成穿孔破壞,隨著撞擊次數的增加,彈靶材料破碎得更細,且熔融態的比例增加,碎片云載荷分布越分散,薄板的變形與破壞模式轉變為中心穿孔及環孔區域大凹陷變形并伴有撕裂。第3 層板阻擋了大部分碎片云能量,第4 層板的彎曲變形比第3 層板小很多,其中心穿孔直徑的測量平均值為46 mm,凹陷變形區域直徑為穿孔直徑的2~3 倍,凹陷板與靶板原平面的夾角較小,約為12°,說明其凹陷變形的速度較小。薄板穿孔四周材料的凹陷變形可簡單類比成圓環的膨脹變形,當膨脹速度大于某值后,圓環在膨脹過程會斷裂成多段。材料起裂后裂紋在板中傳播形成長裂紋,與實驗中薄板撕裂成多塊的結果一致。根據前述分析,第4 層板環孔凹陷區域的變形速度較低,其環向膨脹更趨近于薄板起裂的臨界速度。
2 碎片云作用下環形薄板變形模型
由實驗結果總結得到在分散碎片云載荷下薄板的響應特征如下:薄板中間區域材料在碎片云中部高幅值沖擊載荷下發生穿孔,環孔區域的環向板承受的碎片云載荷稍微小一點,環板材料發生凹陷變形,孔邊材料在凹陷膨脹過程中破碎成幾段,裂紋擴展直至薄板裂成幾塊。碎片云速度分布與環板變形如圖3 所示。碎片云撞擊薄板穿孔尺寸的計算已有研究[10],在此不做考慮,本研究側重碎片云載荷下環形薄板的變形建模。
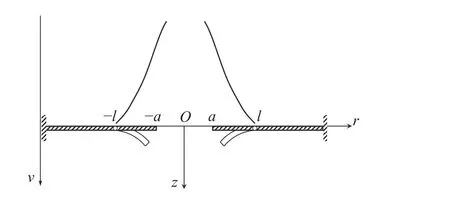
圖3 環板變形側視圖Fig. 3 Lateral schematic of annular plate deformation
2.1 薄板變形假設與一般方程
根據實驗結果可知,碎片云分布載荷作用下的變形屬于典型的薄板大變形問題。薄板在變形過程中發生彎曲,需要考慮彎矩作用,另外薄板面內還有膜應力。要建立薄板變形的一般方程,需作如下基本假設:
(1) 考慮到薄板撓度是板厚的幾倍甚至幾十倍,為此忽略板的彈性小變形,采用理想剛塑性體模型描述薄板變形;
(2) 薄板變形服從Love-Kirchhoff 假設[11],即中面法線變形后仍保持為中面法線,厚度變化忽略不計,同時略去中面法向應力;
(3) 不區分變形前后參考位形的差異,采用變形前的位形作為參考基準建立平衡方程;
(4) 薄板內力除徑向彎矩Mr和環向彎矩Mθ外,還需要考慮徑向膜力Nr和環向膜力Nθ。
基于以上假設,可以建立軸對稱薄板變形過程的橫向、環向和徑向動力學方程[12]
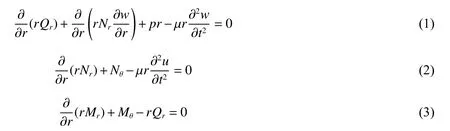
式中:r為徑向坐標,θ 為環向坐標,u為徑向位移,w為撓度,Qr為剪力,μ為板的面密度,p為軸對稱的橫向分布載荷。
考慮面內變形與出面變形的薄板軸對稱幾何方程,其內力(或稱廣義應力[3])徑向彎矩Mr、環向彎矩Mθ、徑向膜力Nr和環向膜力Nθ對應的廣義應變分別為徑向膜應變εr、環向膜應變εθ、徑向曲率κr和環向曲率κθ。幾何方程如下

采用理想剛塑性體模型,材料發生剛性位移或塑性變形,則薄板發生塑性變形時膜力Nr、Nθ達到N0,彎矩Mr、Mθ達到M0

式中:h為板厚度,σy為屈服強度。
薄板材料是理想剛塑性體模型,薄板的應力狀態位于屈服面上,為此采用Hodge[13]提出的包含彎矩、膜力作用的近似屈服準則,如圖4 所示。可以看出,屈服面上的膜力和彎矩獨立作用,各自位于Tresca 屈服面上。這樣的近似處理使求解過程變得非常簡便。另外,橫向剪力Qr出現在平衡方程中,但是由于不考慮其產生的剪切變形,因此不出現在屈服條件中,并且后面計算中可以看到,化簡的平衡方程不包含剪力。
圖4 中mr、mθ、nr、nθ為無量綱內力,mr=Mr/M0,mθ=Mθ/M0,nr=Nr/N0,nθ=Nθ/N0;A、B、C、D、E、F是屈服條件上的角點,各線段代表材料的某一內力狀態。正交法則規定一點廣義塑性應變增量的方向與屈服面外法線方向相同,如圖4 所示。對于具體的問題,在約束允許的機動場中,根據廣義塑性應變增量(或廣義塑性應變率)的方向,可以確定塑性變形由哪一部分屈服面控制,從而為具體問題的求解確定內力大小。
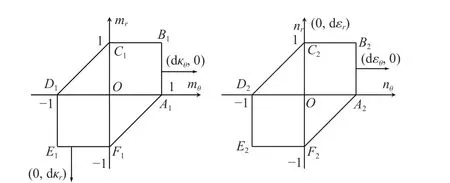
圖4 Tresca 屈服條件與正交法則Fig. 4 Tresca condition and flow rule
2.2 環板變形方程簡化
根據薄板變形方程,結合屈服條件和正交法則,就可以求解薄板變形的初邊值問題,從而得到環板的變形。然而多個偏微分方程的相互耦合以及非線性項的引入,使方程很難得到解析解,需要根據本問題的特征對方程進行簡化。理想剛塑性體的使用、碎片云撞擊載荷的特性以及環板構型的特殊性會使方程變量減少,復雜程度降低。
如圖5 所示,薄板中部發生穿孔(0
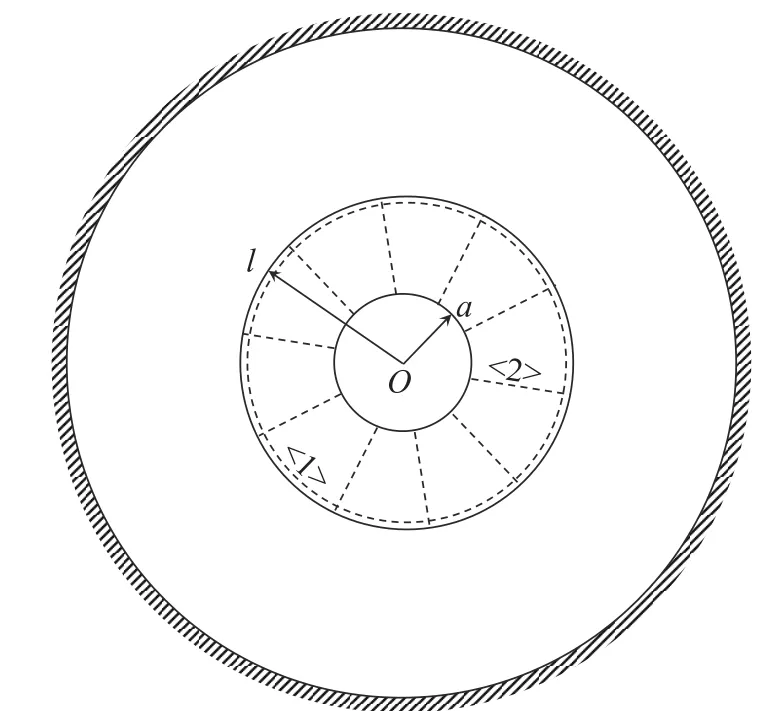
圖5 環板變形俯視圖Fig. 5 Top schematic of annular plate deformation
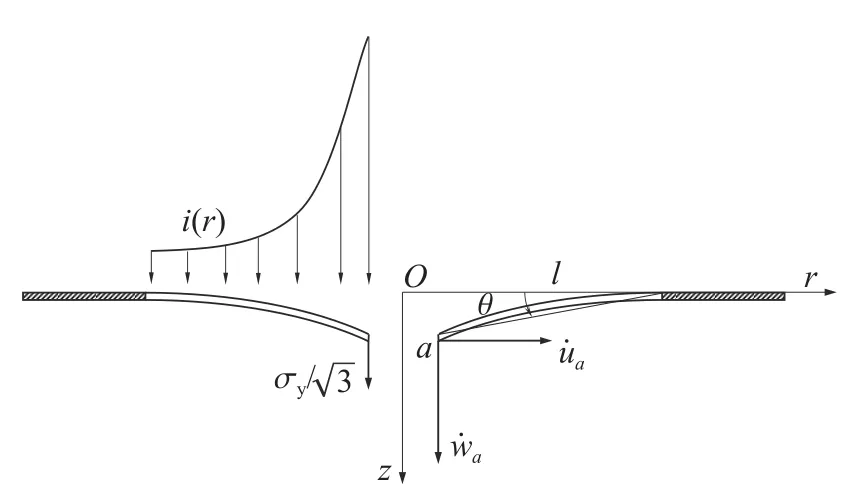
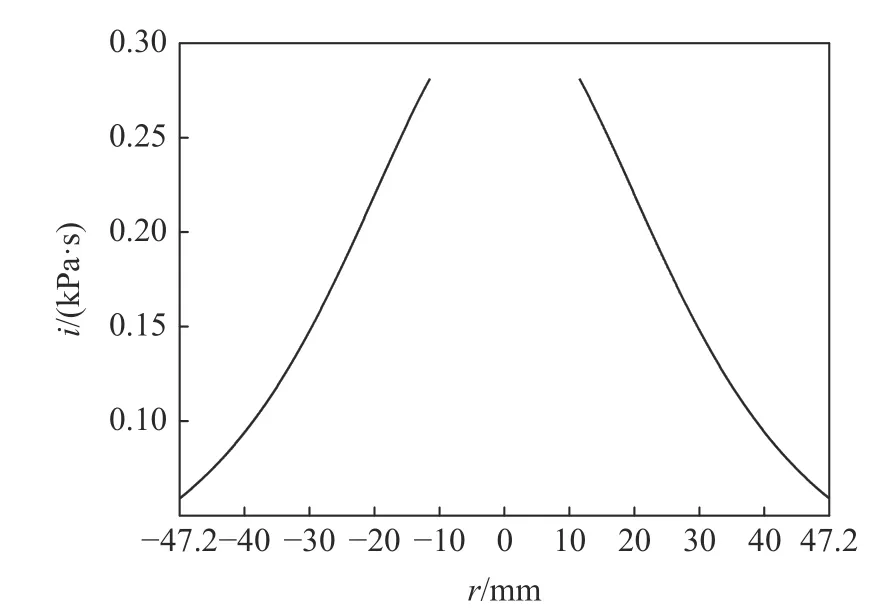
剛塑性環板撓曲變形采用錐形機動場[14],即a≤r 代入式(14),得 由于只有單一未知量,使用能量方程微分形式求解更方便,即塑性鉸上塑性功率與動能變化率平衡 對于a 代入式(34)得到環板凹陷變形終態角度θt 由式(33)和式(34)即可求出環板變形最終撓度wta和終態角度θt,由式(29)可得到環板變形與速度的關系式。下面將計算環板在碎片云撞擊下的具體變形問題,得出環板徑向速度,進而計算環板花瓣型撕裂。 圖6 撓度與徑向關系示意圖Fig. 6 Schematic of relationship between deflection and radial displacement 圖7 沖量載荷下環板變形示意圖Fig. 7 Deflection of annular plate subjected to impulse 為計算環板撕裂起始時的變形,首先計算出環板在碎片云撞擊下達到的最大徑向速度。為得到環板變形時材料受力狀態,將板厚h= 1.5 mm、材料屈服強度 σy= 265 MPa 代入式(8),求得剛塑性彎矩M0和剛塑性膜力N0。根據多次碎片云模型[10],可以計算本研究實驗工況下3 次碎片云對第4 層環板施加的沖量面密度i(見圖8)以及碎片云作用范圍的半徑l= 47.2 mm,再通過式(30)~式(32)求得碎片云撞擊環板時環板的初始動能Ed0= 97.5 J。由式(29)和式(17)得到內環邊徑向速度u˙a隨內環邊撓度wa變化曲線,如圖9 所示,得到最大內環邊徑向速度u˙ma為25.99 m/s。 圖8 沖量面密度載荷分布曲線Fig. 8 Distribution of the impulse per area 圖9 環板內環邊徑向速度與撓度的關系Fig. 9 Relationship between inner edge radial velocity and deflection 上述模型可以用于描述碎片云載荷分布較分散的環形薄板變形,其環板凹陷變形區域集中在碎片云載荷分布區域內,由于載荷不太集中,環板的變形不太快,變形區與未變形區分界的塑性鉸采用駐定塑性鉸,其計算結果與第4 層板的實驗結果相符合。實驗中二次碎片云撞擊第3 層板時的沖量面密度相對較高,第3 層板凹陷變形的速度較快,拉著未變形區域發生凹陷,其變形區與未變形區的塑性鉸是移動的,因此第3 層板的變形需采用移行的塑性鉸圓來描述。對于移行鉸,l=l(t),l˙ ≠0,由圖6 可知,這時內環邊撓度wa和徑向位移ua為 通過超高速撞擊實驗總結了薄板在軸對稱碎片云載荷作用下的變形與破壞模式,并對此完成了建模研究,結論如下: (1) 實驗中薄板在分散的碎片云載荷下經歷中部穿孔,形成環板,環板在剩余碎片云載荷下發生凹陷,孔邊材料繼而發生拉伸破碎,形成花瓣型撕裂; (2) 基于實驗現象與經典理論,建立了環形薄板在碎片云沖擊下的剛塑性變形模型,該模型同時考慮彎矩和膜力,通過簡化得到了環板變形微分方程,可以求解得到板橫向速度場和徑向速度場; (3)將孔周邊的薄板材料膨脹視為圓環的膨脹,根據模型計算得到環板內環最大環向應變率,代入Grady 破碎模型,計算實驗中第4 層板撕裂的花瓣數,另外根據模型還計算得到環板凹陷變形終態角度,計算結果均與實驗結果吻合; (4) 對于高幅值碎片載荷的環形薄板變形,宜采用移行塑性鉸描述變形區域的擴展過程,其變形的理論建模和求解還需要在本研究的基礎上進一步開展。
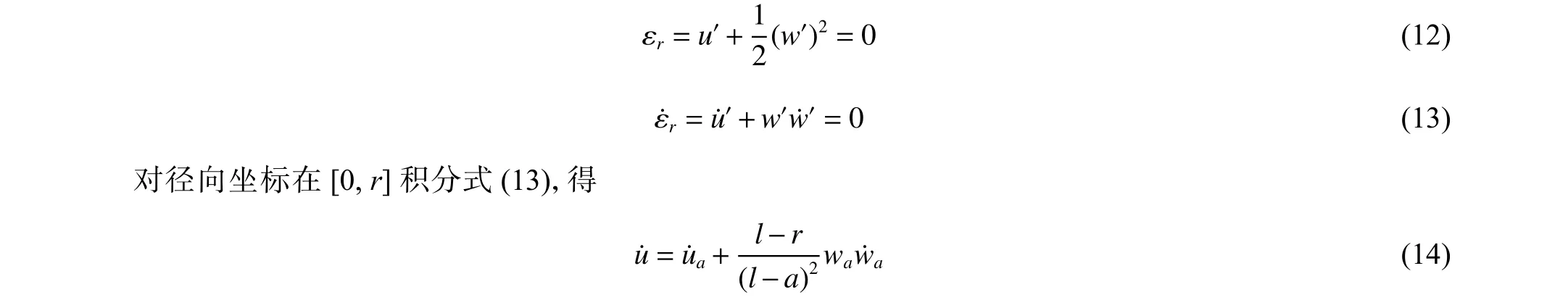



2.3 動力學方程求解



3 計算驗證






4 結 論

