整體把握數學教材?發展學生思維張力

陳憶雯

【摘 要】小學階段，數的認識是培養學生的數感、符號意識、運算能力等核心素養的重要基礎。“小數”作為人類計數歷史上重要的一環，凝聚著人類的創造力與智慧。小數的相關知識在數學“數的認識”中具有至關重要的作用，教師需要采用有效的策略，引導學生去探索數的認識及內容本質，并滲透核心素養中的數學方法;需要研究概念本質、追溯小數的本源、整體把握教材，進行有效的教學，使得學生的數學思維更具生長性和靈活性。

【關鍵詞】小數教學 數學教材 意義 本質

畢達哥拉斯說：“數支配著宇宙。”數的認識是學習數學的基石。“小數的意義”是“數的認識”的一節種子課。理解數的意義、進行數的認識的教學研究，需要教師基于學生的數學學科核心素養，采用有效的策略與方法引導學生去探索、思考與理解數的內容本質，發掘其中體現的數學思想，以便培養學生的數學學科素養。筆者針對“小數”進行了大量的文獻研究，并在教學實踐中多次進行“小數的意義”的對比教學，發現生活中處處都有小數，但學生對于小數意義的理解存在一定困難。本文以“小數的意義”為例，從厘清概念、把握教材和研究數系三個角度，淺談如何整體把握“小數的意義”的教學，同時發展學生的思維張力。

一、厘清概念，分析現狀

（一）研究學生

從目前的教學現狀來看，多數學生認為有小數點的數就是小數，或者比1小的數就是“小數”。這是源于關于小數的概念，教材上給出的定義是“我們可以把分母是10、100、1000的分數寫成一位小數、兩位小數、三位小數……”，這句話指出小數是十進制分數的一種特殊形式。把十分之幾界定為小數的意義，并不能讓學生從本質上去理解小數，學生的理解在課堂上沒有得到正確的解釋，因此出現了概念模糊的情況。

（二）研究概念

教師首先需要厘清概念。人們對數的認識是源于遠古時期“結繩計數”所產生的自然數，自然數是對整數數量的抽象理解。但是后來人們在生產生活中遇到了當測量小于單位“1”的量時，自然數已經無法滿足生產生活的需要，分數和小數也由此產生。比如：1厘米寫成多少分米，用小數來表示就是0.1分米。從這一點來說，小數的教學重點和概念本質應該是用來表示小于單位“1”的數。

（三）研究教學

結合實際教學，對于小數概念的認識，教師不能只是滿足于教學小數的書寫、組成和小數與分數的轉化等，而是需要思考一些更為本源的問題。例如，生活中已經有整數了，為什么還會出現小數？要把構建“小數”背后的數學思想方法用學生易懂的方式表達出來。

二、梳理體系，構建聯系

（一）數的體系的關聯性

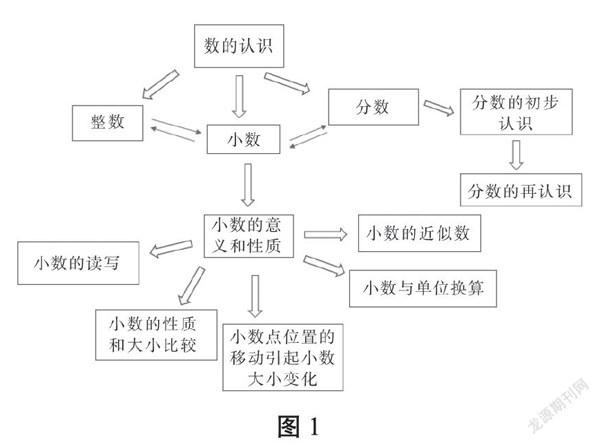
研究小數的意義首先需要研究數的體系。筆者結合整個小學階段“數的認識”的結構，進一步整理了整數、小數和分數的關系模式圖（見圖1）。小數的學習是在學生學習了整數和分數的基礎上展開的，學生對數的認識是從最基本的整數開始慢慢擴展的。因此，教師要把分數和整數、小數和整數聯系起來教學，否則學生就會覺得小數是全新的，與以往學過的知識沒有關系。

小數的本源是數，教師需要遷移學生已有的知識經驗，將小數與整數、分數進行連接﹐讓學生感悟到數的體系內在的統一性，以便引導學生追溯小數的本源，感悟數的統一性。

（二）位置值的統一性

通過位置值將小數和整數聯系在一起。可以借助1和0.1的關系為突破口（見圖2），把十分為10份，得到1，1再接著平均分10份，每份就是0.1。從位值制來看，個位不夠再往下分，需要創造新的數位，個位的右邊就出現了十分位，學生熟悉的100、10、1和新認識的0.1、0.01、0.001就產生了聯系。反過來看，10個0.1是1，10個1是10……與整數的十進制也是相同的。小數和整數正是通過十進制而連接起來了，最直觀的體現就是計數器上從整數數位到小數數位的統一性。為了突破這個教學難點，教師可以利用正方體或者數軸，清楚地向學生解釋兩者之間的關系。

（三）數與生活的密切性

將小數回歸于生活，就能解釋小數和分數的關系。一是小數和分數之間的聯系，小數是分母為10、100、1000……的分數的另一種形式;二是兩者之間的區別，這一點與生活是密切相關的。關于生活中人民幣的使用，如果都用分數，在付錢和找零時會比較麻煩。為了更加方便生活，也為了方便計算，就出現了和整數的位值計數以及算理都比較一致的小數。

三、研讀教材，優化策略

為了更好地把握“數的認識”的教學，教師需要研讀教材，抓住教學內容的重難點，分析教材的編排意圖。筆者在研究小數概念內容的基礎上，分析不同版本的教材，總結出以下三個關鍵教學策略：

（一）依托經驗，引發認知需求

著名數學家兼心理學家斯根普認為，數學概念的教學有基本原則：超過個人已有概念層次的高階概念不能用定義方式來溝通，只能搜集有關例子供其經驗，再靠他自己抽象以形成概念。

有了整數，為什么還需要小數？為了解決這個問題，筆者深入研究了教學內容，對比分析多版本教材的優勢，發現數來源于生活，小數的產生是因為生活的需要。在教學中，教師可以借助生活情境引發小數產生的需求。

例如，人教版數學教材設計了貼近生活的問題情境（見圖3）：用尺子去測量講臺的長度是1米多一點，但是又不到2米，用米做單位多出的部分不夠1米。學生已有的知識無法解決這個問題，認知產生了沖突，不能得到一個整數的結果，自然引發了小數產生的需求。

基于以上分析，筆者在教學中對于小數的引出是通過設計實際的生活情境：測量同學的身高。（見圖4）

【片段1】

師：這名同學的身高是多少米呢？

（學生有點猶豫）

師：能用1.4米表示嗎？

生：不能。

師：能用1.5米表示嗎？

生：也不能。

師：現在用這把尺子能否準確量出他的身高呢？

生：不能。

師：一位小數不能表示這名同學的身高，誰能幫忙改進一下？

生：將這一格再分一分（將0.1米再細分單位成0.01米）。

師：怎么分？

生：平均分成10份。

師：把0.1米也就是1分米平均分成10份，每份是多少？

生：1厘米，也就是米。

師：用小數表示就是0.01米。

從生活出發，通過創設測量學生身高的情境自然而然地引出了小數產生的需求，引發了學生的認知沖突，推進了學生主動思考。這樣的情境設計，沒有刻意地標示課題，但無形中已經在學生心中播下學習小數的種子了。測量身高的過程更是體現出了小數的本質：由于生活中整數無法滿足需求，需要單位的再細分，從而產生更小的計數單位，引出兩位小數的認識。學生學習的種子會生根發芽，思維也潛移默化地影響著他們。

（二）豐富表征，呈現多維視角

華羅庚教授曾說：“數無形時少直覺，形少數時難入微，數與形，本是相倚依，焉能分作兩邊飛。”數學課程標準強調，“數學課程能使學生掌握必備的基礎知識和基本技能，培養學生的抽象思維”。完善小數的意義，要讓學生經歷小數從生活中來，再借助圖形表示數形結合的過程。分析各版本數學教材，其對于小數的表征方式，都采用了從生活到圖形，再到抽象的數的方式。從尺子或者錢幣出發，引出小數的認識，再借助圖形，用正方形表示一位小數和兩位小數，最后由面到體，用正方體來表示三位小數。這樣一種從具體到抽象的過程，從平面圖形到立體圖形的多維遞進，使得學生對小數的認識更加具有層次性。比如：一維的正方形，可以解決學生理解0.1和0.01這一教學難點。教學設計如下：

【片段2】

師：最左邊這一條（見圖5）是把正方形平均分成10份，那每份是多少？

生：0.1。

師：第2條這一小格通過量一量發現也是平均分成10份，每份還是0.1嗎？

生：不是，是0.01。

師：都是平均分成10份，這里為什么是0.01？

生：因為0.1是把正方形平均分成10份，0.01是把0.1平均分成10份。

小數的教學是數的教學，將小數的意義從生活實物再到圖形中的面積關系和體積關系，是一個數形結合的過程。0.1的意義不能局限于生活中的物體，借助幾何可以更加清楚完整地描述小數的意義，0.1不僅存在于長度中、人民幣中，也存在于面積中、體積中……這樣小數意義的構建才是逐步完整的。

以上片段的教學設計不僅體現了幾何直觀的數學素養，也滲透了推理能力的培養。讓學生由如何得到0.1推理出0.01，學生對于小數意義的理解上升了一個臺階。推理能力是數學學習的十大核心概念之一，是數學學習的一種基本思維方式。

（三）借助分數，架構理解橋梁

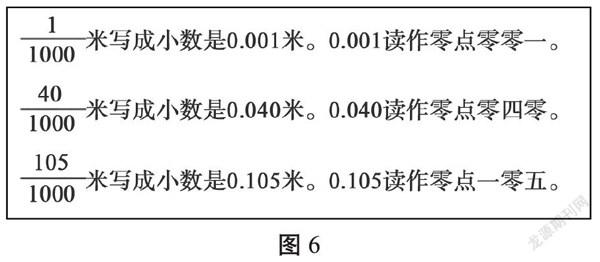
從小數與分數的關系來說，各版本數學教材都是借用分數作為小數理解的橋梁，并沒有直接教學小數，如蘇教版數學教材（見圖6）。

分數與小數是緊密關聯的，小數的實質是一種特殊的分數。在概念的理解上，小數和十進制分數應該有對應的關系，比如0.1和，0.01和……從學生的角度來分析，小數的認識在分數之后，此時學生已經能夠說清分數的意義，在此基礎上學習小數的意義更加水到渠成。例如，目前教學中普遍存在的一個問題：教師不能說清楚什么是一位小數、兩位小數和三位小數，僅僅是從形式上進行概括，像0.01、0.21這樣的小數點后面是兩個數的小數，我們稱之為兩位小數。其實，理解其本質可以借助分數，因此，筆者在教學中借用分數作為理解小數意義的橋梁。

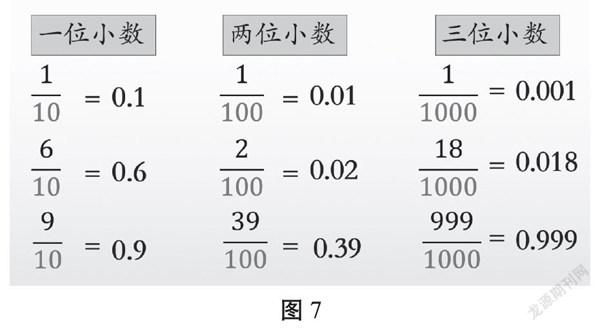
本課內容的教學，在學生知道0.1是一位小數的基礎上，很容易推理出0.01是兩位小數。學生真的理解兩位小數的意義嗎？筆者針對這一問題，認為可以在新授完小數后，進行一位小數、兩位小數和三位小數的對比總結，借助小數和分數的聯系來定義一位小數、兩位小數和三位小數（見圖7）。

【片段3】

師：0.1、0.6和0.9我們知道是一位小數，今天我們學習的是幾位小數？第二列都是？

生：兩位小數。

師：第三列都是？

生：三位小數。

師：你發現了什么？

生：分母為10的分數可以寫成一位小數，分母為100的分數可以寫成兩位小數，分母為1000的分數可以寫成三位小數。

由此，教師巧妙地借助分數和小數的聯系對幾位小數進行了定義，對比總結出了不同數位的小數和分數的關系。往下再思考，學生還能說出四位小數、五位小數就是分母為10000、100000的分數……學生對于數的思維的理解從淺層的數形式理解提升了一個臺階：原來小數和分數是有關系的。如此，通過知識的聯系提升了學生思維的發散性。

小數的意義是數的認識教學中值得持續研究的主題，有一些可以遵循的規律，還有許多需要探索的問題。小數的認識教學，需要對教材進行整體的研讀，把握教學重點，突破教學難點，思考小數的教學的本質，提升學生的數學素養和思維的張力。

注：本文系江蘇省教育科學“十二五”規劃2015年度重點課題“小學數學高效教學的校本實踐研究”（編號：B-a/2015/02/045）的研究成果。

【參考文獻】

[1]徐明旭.深入研讀教材，把握教學實質——《小數的意義》教材對比研讀[J].數學教學通訊，2016（22）.

[2]馬云鵬.“數的認識”及其教學設計 [J].小學數學教育，2018（3）.