基于特征正則稀疏關聯的無監督特征選擇方法

白圣子，降愛蓮

(太原理工大學 信息與計算機學院，山西 晉中 030600)

0 引 言

在原始高維數據集中，冗余特征的存在會影響學習算法的性能，降低學習算法的效率，甚至遭遇“維數災難”。因此，需要通過特征選擇，從原始數據中剔除無關、冗余等特征，選出具有代表性的特征構成最優特征子集，從而降低數據維度、簡化學習模型、提高學習效率。由于數據規模較大以及獲取數據標簽十分耗時等原因，無監督特征選擇在實際處理中更實用，研究其方法更具有挑戰性[1]。

無監督特征選擇方法根據評價準則主要分為過濾式方法、封裝式方法和嵌入式方法[2]。過濾式方法獨立于具體的學習算法，逐一對特征進行評分，如方差選擇法[3]和拉普拉斯得分[4]選擇法。封裝式方法是根據后續使用的算法每次排除若干特征，直到特征數滿足算法的要求，如遞歸消除特征法[5]。這兩類方法評價標準單一，忽略特征之間的相關性，造成特征的冗余。嵌入式方法是將特征選擇和訓練模型的過程相結合，模型優化的同時直接計算出每個特征的權重，特征權重越大表明該特征越重要。如文獻[6]將特征選擇轉化為矩陣分解問題，利用正則化矩陣分解方法選擇出具有代表性的低維特征子集，但計算復雜度較高且正交約束條件很難應用到實際中。文獻[7]提出特征級自表示選擇方法，將特征選擇問題轉化為損失函數模型。該方法提出了數據集中的每個特征都可以被所有特征線性近似表示的性質，通過優化損失函數可以有效批量地評估每個特征的重要性。但在計算過程中，由于每個特征參與其自身的重構[8]，導致權重易向自身傾斜，無法合理地為每個特征分配權重。

針對上述問題，提出基于特征正則稀疏關聯的無監督特征選擇方法(feature regularized sparse association，FRSA)。該方法利用特征稀疏關聯性質，能夠合理分配特征權重，剔除冗余無關特征，降低數據維度，有效提升數據聚類準確率。

1 FRSA模型建立

1.1 最小二乘法線性回歸

給定一個數據矩陣X∈Rn×m與響應矩陣Y=[y1,y2,…,yc]∈Rn×c，我們通常用如下公式來構建X與Y之間的線性關系

(1)

其中，W∈Rm×c是特征權重矩陣，l(Y-XW)是損失項，D(W)是對W施加的正則約束項，λ是一個正常數。式(1)的目標是得到一個合適的W，使得實際的響應矩陣Y與預測的XW之間的差值最小[9]。

1.2 特征稀疏關聯

本文將數據矩陣X作為最小二乘回歸模型中的響應矩陣Y來測量誤差，學習特征權重矩陣W，揭示原始數據中特征之間的稀疏關聯關系，即某一個特征可以被其它特征(不包含自身)稀疏近似表示。具體地說，給定m個特征，我們所運用的特征稀疏關聯是學習每個特征與其它所有特征之間的線性近似關系。當i=j時，令wji=0，第i個特征不參與自身重構表示

f1≈f10+f1w21+…fiwi1+…+fmwm1

f2≈f1w12+f20+…fiwi2+…+fmwm2

?

fm≈f1w1m+f1w2m+…fiwim+…+fm0

(2)

因此，數據矩陣X中的每一個特征fi可形式近似表示為

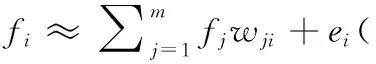
(3)

其中，ei是誤差項，wji是表示系數，fi是數據矩陣X的一個特征。對于所有的特征，式(3)可以寫成

X=XW+E

(4)

其中，W∈Rm×m與E∈Rn×m分別是特征權重矩陣和殘余誤差項。W有效地表示了不同特征之間的關聯關系，并且使得殘余誤差項E(E=X-XW)盡可能得小。

1.3 目標函數

本文利用Forbenius范數來度量誤差大小，期望得到一個合適的W，使得重構后的矩陣XW能夠很好地近似表示原始數據矩陣X。如果X是一個單位矩陣使得誤差項E≡0，則W為平凡解。因此，必須添加正則化項D(W)對特征權重矩陣的解空間進行約束，防止過擬合，降低模型復雜度，得到穩定可行的最優解[10]，進而得到了如下最小化問題

(5)

(6)

2 優化算法

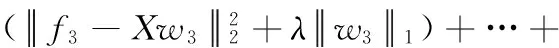
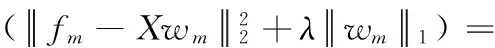
因此，原目標函數展開得到如下m個子問題

(7)

根據特征稀疏關聯關系，第j個特征不參與自身的線性近似表示，因此wj的第j個元素為0。在實際計算過程中，需要刪除數據矩陣X的第j列與wj的第j個元素

(8)

?j∈R(m-1)×1是wj刪除第j個元素0后得到的特征向量，Xj-∈Rn×(m-1)是數據矩陣X刪除第j列得到的數據矩陣，這樣保證了第j個特征不參與自身的線性近似表示。針對式(8)的正則化回歸問題，將利用一種收縮閾值迭代算法求其最優解。

首先考慮式(8)無正則化約束下的連續可微函數最小化問題

(9)

s.t.??,y∈Rn

(10)

(11)

對于g(?)最小的常數K稱為李普希茨常數L。同時，在?k附近可將g(?)通過二階泰勒式展開

(12)

式(11)得出李普希茨常數L形式與二階導數形式相似。基于此，在?k附近可以把函數值近似為

其中，后兩項是與?無關的常量。顯然，式(12)的最小值在如下?k+1獲得

(13)

(14)

即在每一步對g(?)進行梯度下降迭代的同時考慮1-范數最小化。

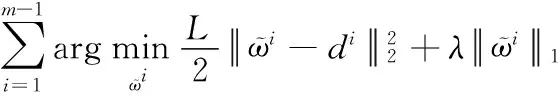
(15)

其中，不存在?i?j(i≠j)這樣的項，即?的各分量互不影響且1-范數是可拆分函數，可得最優閉式解[15]。

對于式(15)中的每一個分量，都可以通過偏導求其最小值

(16)

(17)

其中，sign(x)為符號函數，如果x大于0，則為1；如果x小于0，則為-1；如果x等于0，則為0。考慮到式(15)兩邊都有?i，利用收縮閾值迭代[16]進行求解

(18)

綜上所述，得出式(8)的優化迭代公式

計算g(?)在?k處的偏導，最終得到收縮閾值迭代式

?k+1=Γλ/L(?k-2/L(Xj-)T(Xj-?k-fj))

(19)

文獻[16]已驗證，若X為數據矩陣，當李普希茨常數L=2βmax(XTX)(βmax(·)表示矩陣的最大特征值)，式(19)得以快速求解。該式每次使用前一步迭代求得的近似函數最小值點?k作為下一步迭代的起始點，收斂速度為O(1/k)。為了加快其收斂速度，將引入梯度加速策略Nestrerow加速技術[17]

(20)

(21)

其中，Nestrerow加速使用前兩步迭代過程的結果xk-1，xk，對其進行線性組合生成下一步迭代的近似函數起始點yk+1。經驗證[17]，該加速技術適用于式(19)的收縮閾值迭代算法，以極少的額外計算量提高了算法的收斂速度。因此，引入Nestrerow加速后，式(19)為如下迭代形式

(22)

算法1：

輸入：數據矩陣X∈Rn×m，特征選擇個數d，正則項參數λ；

輸出：特征子集D∈Rn×d；

(1)數據矩陣X→{f1,f2,…,fm}；

(2)將式(6)劃分為m個子問題：

(3)計算L=2βmax((Xj-)TXj-)，初始化y1=?0，t1=1；

(4)重復(k≥1)：

?k=Γλ/L(yk-2/L(Xj-)T(Xj-yk-fj))

(5)直到收斂；

在引入Nestrerov加速后，收斂速度從O(1/k)提高到O(1/k2)。式(17)求偏導時(Xj-)TXj-的計算復雜度為O(nm2)，所以每個子問題的計算復雜度為O(nm3/k2)。因為FRSA模型的最優解是由m個子問題的最優解整合得到，所以該算法的整體計算復雜度為O(nm3/k2)。

3 實驗分析

3.1 實驗數據

為驗證本文方法的性能，在機器學習數據庫中選取了6個標準數據集進行對比測試，各數據集的詳細參數見表1。

表1 實驗數據集參數匯總

3.2 實驗對比方法

為了驗證本文提出的FRSA方法的有效性，實驗中將其與以下4種常用的無監督特征選擇方法進行比較：

(1)拉普拉斯得分特征選擇方法[18](Laplacian score feature selection，LS)；

(2)無監督判別特征選擇方法[19](unsupervised discriminative feature selection，UDFS)；

(3)矩陣分解特征選擇方法[20](matrix factorization feature selection，MFFS)；

(4)自表示特征選擇方法[7](self-representation feature selection，SR-FS)。

3.3 實驗設置

在本實驗中，采取3種被普遍應用的評價指標，即聚類準確率(accuracy，ACC)、歸一化互信息(normalize mutual information，NMI)和冗余率(redundancy rate，RED)來評價不同無監督特征選擇方法的性能。對于一個輸入樣本xi，qi和pi表示它的聚類結果和真實標簽，那么ACC的定義如下

(23)

其中，函數δ(x,y)用于判斷x與y是否相等，若相等則函數值為1，否則函數值為0。map(qi)是一個最佳映射函數，它的功能是通過Kuhn-Munkre算法把實驗得到的聚類標簽與樣本的真實標簽進行匹配[21]。ACC的值越大說明聚類性能越好，表明獲得的聚類標簽更加接近樣本真實的標簽。

歸一化互信息是評價聚類結果好壞的常用指標之一，給定任意兩個變量P和Q，NMI可以被定義為

(24)

其中，H(P)和H(Q)分別表示P和Q的熵，I(P,Q)是P和Q兩者之間的互信息。P是聚類結果，Q是實際標簽。類似于ACC，NMI的值越大意味著聚類性能越好。

冗余率[22]是用來度量數據的特征之間是否具有較強的相關性。假設fs是所選擇的特征集，冗余率計算公式如下

(25)

其中，ρij是特征fi與特征fj之間的相關系數。RED(fs)的值越大意味著選擇后的許多特征仍然是顯著相關，冗余程度高。因此計算所得的冗余率越小越好。

在實驗中將對每個無監督特征選擇方法的參數進行設置。對于所有方法，每個數據集選擇特征的個數范圍設置為 {20，30，40，50，60，70，80，90，100}。對于LS、UDFS算法，將它們的近鄰參數k設置為5。對于有正則項參數的算法，采用交替網格搜索的方式確定它們的值，其網格搜索范圍設置為 {0.001，0.01，0.1，1，10，100，1000}[6]，并記錄其中最優參數所對應的最好結果。然后將9個不同維數的特征子集的聚類準確率、歸一化互信息以及冗余率分別取平均值，作為評價各方法性能的指標。

當利用K-means算法對每種方法選擇的低維特征進行聚類時，考慮到K-means聚類的性能會受到初始質心選取的影響，為提升結果準確度，將重復執行150次不同的隨機初始化實驗，然后記錄平均結果。

3.4 實驗結果與分析

利用合成數據集IRIS-20測試本文提出的FRSA方法是否能找到具有代表性的特征。該數據集包含150個樣本和20個特征，后16個特征是由前4個特征線性組合得到(組合系數隨機生成并且和為1)，并加入了一定的高斯白噪聲。

圖1 特征權重直方圖

從表2和圖2(e)的實驗結果可知，FRSA方法在Lung_discrete、Pronstate_GE、lymphoma、ORL和Urban這5個在數據集中所選擇的特征子集獲得最高的聚類準確率(ACC)，在數據集COIL20上的聚類準確率僅次于MFFS方法。從表3和圖2(c)的實驗結果可知，FRSA方法在Lung_discrete、Pronstate_GE、ORL、COIL20和Urban這5個在數據集中所選擇的特征子集獲得最高的歸一化互信息(NMI)，在數據集lymphoma上的歸一化互信息僅次于SR-FS方法。聚類準確率和歸一化互信息都是評價聚類結果好壞的常用指標，因此得出結論，FRSA方法選擇出的特征更具有代表性，可以有效地提高聚類準確率。從表4和圖2(c)、圖2(d)的實驗結果可知，FRSA方法在Lung_discrete、Prostate_GE、COIL20和Urban數據集上選出的特征子集的冗余率(RED)最低，在數據集lymphoma上的冗余率僅次于SR-FS方法，在數據集ORL上的冗余率僅次于MFFS方法。冗余率越低，冗余程度越低。表明FRSA方法選出的特征之間冗余程度較低，特征子集冗余率較低，更具有代表性。

表2 不同特征選擇算法的聚類準確率ACC/%

表3 不同特征選擇算法的歸一化互信息NMI/%

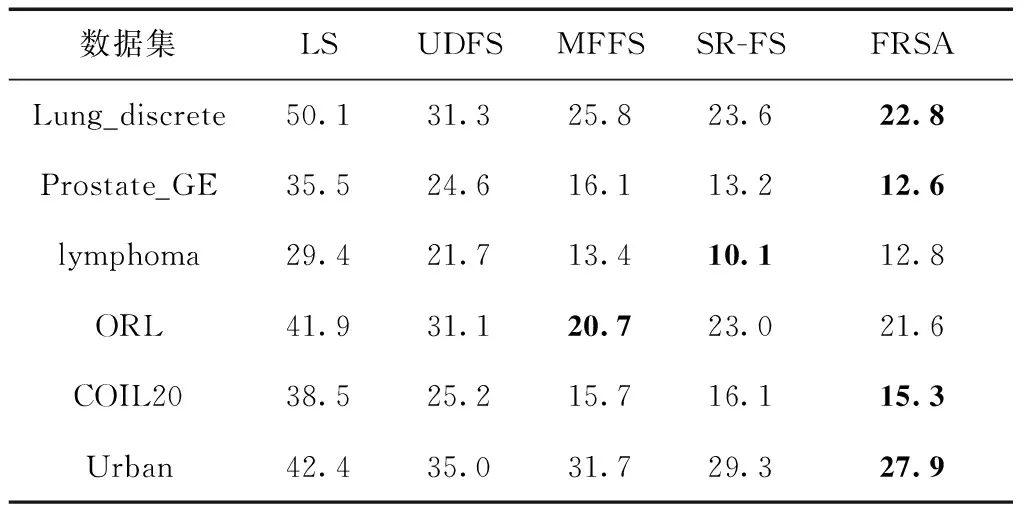
表4 不同特征選擇算法的冗余率RED/%

圖2 5種無監督特征選擇方法在6種不同數據集上的ACC、NMI、RED對比

通過以上分析可以得出，由于LS方法是對特征逐一進行評分選擇，并且沒有考慮特征之間的相關性，因此在其3個評價指標上明顯弱于其它方法。UDFS、MFFS、SR-FS方法都是基于正則化選擇，并且都是對特征進行批量選擇，因此在特征選擇時，批量選擇的效果優于單個選擇。但是，UDFS方法更多地是考慮樣本之間的相似，容易忽略特征之間潛在的相關系。MFSS方法是從子空間學習角度進行特征選擇，也沒有考慮特征之間的相關性。而SR-FS方法雖然利用特征級自表示性質選擇特征，考慮特征之間的相關性，但不足之處是特征參與自身重構時容易使特征權重向自身傾斜，導致權重分配不合理。因此，本文在特征級自表示的損失函數模型框架下，利用特征互表示的性質[8]，學習每個特征之間的關聯關系，提出了基于特征正則稀疏關聯的無監督特征選擇方法(FRSA)。該方法不僅利用稀疏正則化約束對特征進行批量選擇，而且考慮到每個特征與其它特征(不包括自身)的關聯性。實驗結果表明,該方法所選出的特征子集具有較好的聚類效果和較低的冗余度，性能優于其它4種常用的無監督特征選擇方法。在計算復雜度方面，UDFS方法、MFSS方法和SR-FS方法采用矩陣直接迭代逼近最優解，計算時間與空間復雜度較高[23]。而分治-收縮閾值迭代算法將矩陣整體優化問題拆分為多個性質相同的向量優化問題，然后再進行迭代求解，占用內存較小且計算效率高。因此，FRSA方法有較低的計算復雜度。

4 結束語

在本文中，利用無標簽數據特征之間潛在的關聯性，提出了一種基于特征正則稀疏關聯的無監督特征選擇方法(FRSA)。利用L1-稀疏規則算子在特征選擇時對權重矩陣施加正則化約束，最小化其非零行數，加強了特征權重矩陣的行稀疏性，提升了所選特征子集的魯棒性。通過稀疏關聯性質克服了特征權重易向自身傾斜的不足，合理地為每個特征分陪權重。實驗結果表明，FRSA方法可以有效地評估每個特征的重要性，選擇出重要特征，剔除冗余特征，降低原始高維數據的冗余率，提高聚類準確率，并且具有較低的計算負責度。在實際應用中，獲取的數據不夠完善不具有多樣性[24]，后續工作可以進一步擴展方法適用于不完整數據。另外，正則化約束項[25]對權重矩陣的作用直接影響到FRSA方法的性能，如何構建更有效的正則化約束項也是下一步研究重點。