基于BP神經網絡的離港航班滑出時間預測
黃龍楊,夏正洪
(中國民用航空飛行學院 空中交通管理學院,四川 廣漢 618307)
0 引 言
滑出時間是指離港航班從停機位推出開車并滑行至起飛的時間間隔,它是評估繁忙機場場面運行效率的主要性能指標[1]。目前,多數機場仍然采用基于經驗的滑出時間來對離港航班進行管制指揮,而實際滑出時間與經驗滑出時間往往相差甚遠,航班的過早推出或不恰當的滑出時機都將導致出現不必要的擁堵、延誤和燃油消耗,并且將嚴重影響機場場面運行效率。因此,科學準確地預測離港航班的滑出時間,在此基礎上實現對離港航班的推出和滑行時機進行控制,對于提升機場場面運行效率以及節能減排至關重要。
國外關于滑出時間預測的研究始于21世紀初,現有成果分析了離港航班滑出時間主要影響因素[2],主要包括離港隊列長度、滑行距離、機場場面交通流、跑道運行模式、滑行過程中的轉彎個數、是否是低能見度天氣等。離港航班的滑出時間預測方法大致可分為3類:①基于排隊論的滑出時間預測方法[3]。②基于快速仿真的滑出時間預測方法[4]。③基于歷史數據挖掘的滑出時間預測方法,主要用到的算法包括貝葉斯網絡[5]、支持向量機[6,7]、強化學習[8]、深度學習[9,10]等。國內關于離港航班滑出時間預測的研究還處于起步階段,部分學者針對單跑道機場離港航班滑出時間進行了預測研究[3-7]。但是,現有預測結果的精度有待提高,未考慮多跑道運行模式對滑出時間的影響。由于跑滑系統結構及交通流特點不同,國外已有研究成果不能直接應用于國內大型樞紐機場的離港航班滑出時間預測中。
因此,本文提出了一種雙跑道運行模式下的離港航班滑出時間預測方法,該方法綜合考慮了機場場面交通流、運行模式、平均滑出時間、滑行距離等多種影響因素,在對比分析相關性的基礎上,構建了基于BP神經網絡的離港滑出時間預測模型,以期通過對滑出時間科學準確的預測,優化離港航班的推出開車時刻,從而提升機場場面運行效率,減少不必要的燃油消耗和污染排放。
1 滑出時間影響因素及相關性分析
1.1 影響因素
大型樞紐機場離港航班的管制流程如下:首先塔臺放行席位管制員根據預計起飛時間依次向離港航班發布ATC(air traffic control)許可,然后由地面管制席位管制員發布推出開車許可,記錄離港航班的實際撤輪檔時間(actual off block time,AOBT),并給出離港航班的滑行路線至跑到外等待點加入等待隊列,如果在滑行的過程中存在滑行沖突,則還需要進行場面的沖突調配,最后由塔臺管制席位管制員發布進入跑道起飛的指令,并記錄其實際起飛時間(actual take off time,ATOT)。因此,離港航班滑出時間(taxi out time,TOT)等于該航班離港實際起飛時間與實際撤輪檔時間之間的差值
TOT=ATOT-AOBT
(1)
通過文獻追蹤可知,離港航班的滑出時間影響因素較多,受機場場面交通流的影響,航班之間會爭奪跑道、滑行道資源,這必然會導致某航班的等待,從而使得它的滑出時間與其無障礙滑出時間[4]有較大的偏差。同時,滑出時間還受到流量控制、惡劣天氣、航空公司、管制員、旅客、轉彎個數等因素的影響,但是這些因素或不可量化,或影響較小,故在本文不予考慮。因此,離港航班滑出時間的主要可量化因素包括:同時段推出的離港航空器數量、同時段滑行的起飛航班數量、同時段滑行的落地航班數量以及滑行距離4種。考慮到機場地面交通流有明顯的小時變化特征,本文創新性地引入半小時平均滑出時間、小時平均滑出時間兩個可量化的影響因素。
1.2 相關性分析
基于我國中南某機場2019年5月26日至6月8日的實際運行數據,可計算得出每一架離港航班的實際滑出時間、平均滑出時間、同時段滑出的離港航空器數量、同時段推出的航空器數量、同時段滑行的進港航空器數量,再結合機場場面地圖可以求出滑行距離,然后分析實際滑出時間與這6種影響因素之間的相關性如圖1所示。
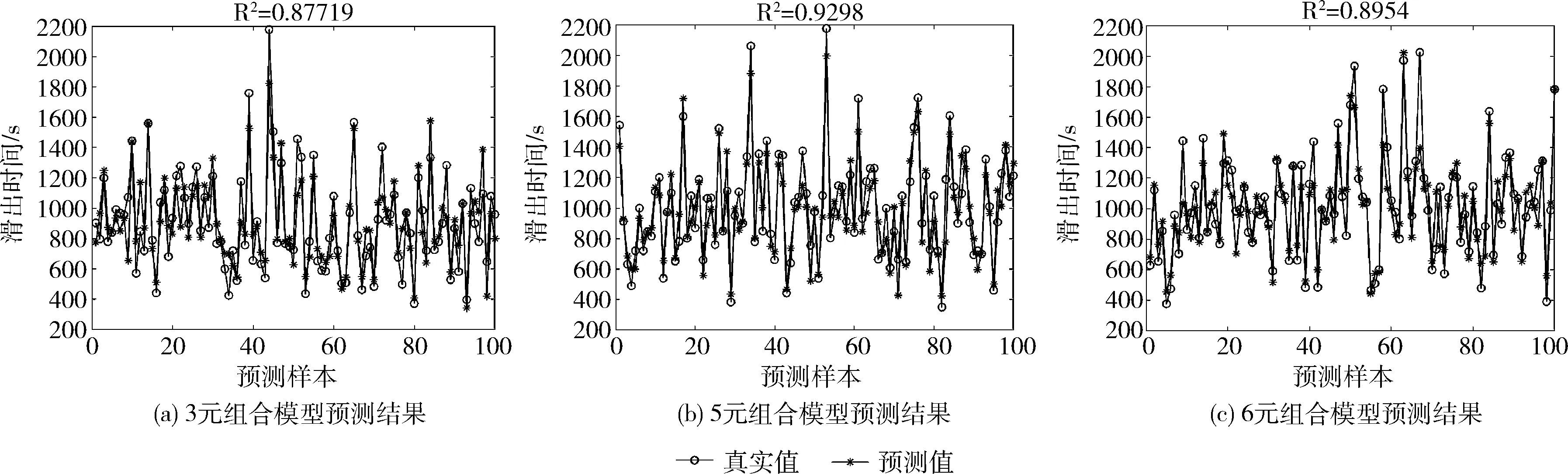
圖1(a)是滑出時間與同時段滑行的離港航班數量的相關性,其相關系數為R=0.7084。根據相關性強弱判定規則[11]可知:同時段滑行的離港航班數量與滑出時間呈現強相關性(R>0.6)。圖1(b),圖1(c)分別表示滑出時間與同時段滑行的落地航班數量、同時段推出的離港航空器數量,其相關系數分別是R=0.6595和R=0.6122,表明以上兩個因素與滑出時間強相關。圖1(d),圖1(e)分別表示以半小時為時間片的離港航班平均滑出時間、以1 h為時間片的離港航班平均滑出時間與滑出時間之間的相關性,其相關系數分別為R=0.5842和R=0.5012,表明以上兩個因素與滑出時間呈現中度相關的關系(0.3 圖1 離港航班滑出時間影響因素相關性分析 根據相關性分析可知,滑出時間與機場場面交通流呈現強相關性,因為離港航班與離港航班、離港航班與進港航班會因為爭奪滑行道、跑道資源而導致滑出時間增長的情況。根據調研可知,進港高峰時段采用雙跑道相關平行進近模式,進港航班可經由15號和16號跑道落地。此時,若其停機位在西側停機坪,則滑行路線會在滑行道A、B上與15號跑道起飛的離港航班滑行路線有交叉沖突;若其停機位在兩條跑道之間的機坪,則滑行路線會在C、D上與離港航班的滑行路線有交叉、匯聚,由于優先級的原因管制員將指令離港航班在交叉道口等待避讓滑行沖突。在非進港高峰時段采用雙跑道隔離運行模式,此時16號跑道落地的航班與15號跑道起飛的航班之間可能在滑行道G、D上產生交叉沖突;同時,使用15號跑道起飛的航班之間滑行路線可能有交叉、匯聚。因此,該機場雙跑道運行模式下進離港航班之間、離港航班之間都會相互影響,導致離港航班滑出時間、平均滑出時間增加,嚴重影響機場場面的運行效率。 (1)同時段滑行的離港航班數量x1,單位架次。表示航班j的實際起飛(tATOT(j))時間剛好落在航班i的實際推出開車時間(tAOBT(i))和實際起飛時間(tATOT(i))之間的所有離港航班數量 (2) (2)同時段滑行的進港航班數量x2,單位架次。表示航班j的實際落地時間(tALDT(j))剛好落在航班i的實際推出開車時間(tAOBT(i))和實際起飛時間(tATOT(i))之間的所有離港航班數量 (3) (3)同時段推出的離港航班數量x3,單位架次。表示航班i的實際推出開車時間(tAOBT(i))剛好落在航班j的實際推出開車時間(tTOBT(j))和實際起飛時間(tATOT(j))之間的所有離港航班數量 (4) (4)以半小時為時間片的平均滑出時間x4,單位秒(s)。根據機場地面交通流呈現典型的時變特征,在離港早高峰、晚高峰以及進港高峰等典型繁忙時段,離港滑出時間會顯著增加,且由于該機場離港滑出平均時間約為16 min,因此半小時平均滑出時間將成為離港滑出時間的一個重要解釋變量。 (5)以1 h為時間片的平均滑出時間x5,單位秒(s)。綜合考慮交通流、惡劣天氣、流量管制、跑道運行模式以及人為因素的影響,該機場離港航班滑出時間會遠大于平均值,甚至大于30 min,因此以1 h平均滑出時間作為自變量將更好地解釋離港航班的滑出時間。 (6)離港航班滑行距離x6,單位米(m)。大型樞紐機場往往存在多個停機坪區域,離港航班從各停機位推出并滑至跑到外等待點的標準路線略有不同,導致其滑行距離及滑出時間存在較大差異。因此,離港航班滑行距離也是滑出時間的一個可量化的解釋變量。 BP神經網絡是目前使用最廣泛的神經網絡結構,具有任意復雜的模式分類和多維函數映射能力,被廣泛應用于模式識別、分類、預測等領域[12]。為進一步分析討論不同相關性的影響因素對滑出時間的影響程度,本文將神經網絡的輸入分為3種情況,見表1。 表1 BP神經網絡輸入分類 表1中,3元組合預測模型僅考慮強相關的影響因素對滑出時間的影響;5元組合預測模型僅考慮強相關和中度相關的影響因素;6元組合預測模型將綜合考慮所有的可量化影響因素。BP神經網絡的隱層均采用10個神經元,輸出即為滑出時間預測結果。基于以上分析,構建了基于BP神經網絡的離港航班滑出時間預測模型如圖2所示。 圖2 基于BP神經網絡的滑出時間預測模型 基于BP神經網絡的滑出時間預測步驟如下:①在Matlab中載入所有訓練樣本數據,并將其進行歸一化處理;②構建BP神經網絡并根據網絡參數設置原則設定其參數[12],最大迭代次數1000次,學習率為0.01,目標收斂誤差為0.001;③對樣本數據進行訓練,并更新權值和閾值直到網絡趨于穩定;④從訓練樣本中隨機選擇100個數據作為測試集數據,代入神經網絡進行預測,將結果進行反歸一化,并計算預測結果的性能指標。 本文的研究對象是我國中南某樞紐機場,其跑滑系統結構如圖3所示。東跑道3400×45 m,西跑道3800×60 m,東西跑道之間間距約為1590 m,可根據交通流情況選擇隔離運行模式或者相關平行進近模式。 圖3 中南某機場跑滑系統結構 本文所用數據來源于該機場2019年5月26日至6月8日的實際運行數據,數據集共有記錄12 323條,其中包含5690架次離港航班和6633架次進港航班,每條記錄由飛機呼號、機型、實際起飛時間、實際撤輪檔時間、實際落地時間、跑道號、停機位等關鍵信息組成。通過對數據整理分析,得到該機場場面交通流小時分布如圖4所示。 圖4 機場場面交通流小時分布 可見,該機場場面交通流呈現典型的小時變化特征:從凌晨1點到6點,起降架次迅速減少到最低值(約18架次);隨著早高峰的到來,起降架次迅速增加并在10點達到次高點(約51架次);隨著進港航班架次增加,起降架次的峰值在13點達到峰值(約55架次),之后基本穩定在48架次左右。 (1)刪除數據集中的重復記錄。將所有數據按跑道號進行進港、離港航班分離,所得的數據分別以起飛時間和落地時間做升序排序。由于跑道運行模式為隔離運行或相關進近,即不可能在同一時刻有兩架起飛或落地,因此對于起飛時間或落地時間相同的記錄僅保留一條,其余數據則視為異常數據刪除。 (2)刪除數據集中實際起飛時間、實際撤輪檔時間、實際降落時間、跑道號等關鍵信息為空的異常數據。 (3)刪除數據集中滑出時間異常的數據。通過數據分析可知,數據集中有92.5%的航班采用15/16號跑道起降,僅有7.5%的航班由于瞬時風向、風速原因而采用33/34號跑道起降。這種換跑道運行方向的情況往往會導致單架離港航班的滑出時間嚴重偏離平均值,應視為異常數據刪除。 (4)整理后的數據集包含使用15號跑道所有離港航班5428架次,以及使用15號和16號落地的所有進港航班6576架次。 (5)將整理后的數據集中的所有離港航班數據和進港航班數據作為基礎數據,依次求出每一個離港航班的滑出時間、半小時平均滑出時間、小時平均滑出時間、同時段滑行的離港航班數量、同時段滑行的進港航班數量、同時段推出的離港航班數量、滑出距離。最終獲得離港航班滑出時間訓練樣本數據5248條,見表2。 表2 訓練樣本數據 基于Matlab中的神經網絡工具箱進行編程,將樣本數據集進行訓練,然后隨機選擇100個數據作為測試集數據,對本文所構建的模型進行數值模擬,預測結果及誤差分布情況對比如圖5和表3所示。 表3 滑出時間預測結果誤差分布對比 圖5 基于BP神經網絡的滑出時間預測結果對比 從預測值對真實值的擬合程度來看,3種預測模型均能實現對離港航班滑出時間的有效預測,且5元組合預測模型的效果最佳。其中,3元組合預測模型的曲線擬合優度R2=0.8772,模型中僅考慮了強相關的場面交通流,而未考慮平均滑出時間對滑出時間的影響,因此預測結果與真實值偏差稍大。5元組合預測模型的曲線擬合優度高達R2=0.9298,該模型綜合考慮了地面的瞬時交通流,交通流的時變特征,平均滑出時間等多種主要因素,因此預測結果與真實結果之間的偏差最小。6元組合預測模型的曲線擬合程度為R2=0.8954,較5元組合預測預測模型擬合程度反而降低了,說明弱相關性的滑行距離引入后對滑出時間預測結果是不利的。 從預測結果的誤差分布情況來看,滑出時間預測準確率隨誤差范圍偏差的增大而增加,且5元組合預測模型的預測結果最佳。3元組合預測模型結果誤差范圍在±300 s以內占比88%,說明考慮強相關的影響因素的預測結果基本達到預期。在此基礎上加入中度相關影響因素后,5元組合預測模型預測準確率將達到最佳,誤差范圍在±300 s以內占比96%;預測結果偏差最小值為1.02 s,偏差最大值為349.32 s,平均偏差值約為124 s。最后,綜合考慮強相關、中度相關和弱相關影響因素的6元組合預測結果反而有所下降。以上數據比現有國內外所有的離港航班滑出時間預測精度更優[3-7],充分驗證了本文所構建的考慮可量化的滑出時間預測模型的有效性和合理性。 本文基于預測結果的平均絕對誤差百分比(MAPE)、平均絕對誤差(MAE)、均方根誤差(RMSE)對模型進行評價。其中,平均絕對誤差能反映了預測值誤差的實際情況,平均絕對誤差百分比反映了預測結果與真實值的平均偏離情況,均方根誤差反映了預測模型輸出結果離散程度和穩定性。3元組合預測模型的滑出時間預測結果MAPE為14.14%,MAE為120.75 s,RMSE為154.24 s,預測結果已然到達現有參考文獻中的效果。5元組合預測模型的滑出時間預測結果精度最佳,MAPE為10.61%,MAE為90.24 s,RMSE為114.02 s。6元組合預測模型的預測精度較3元組合預測模型高,較5元組合預測模型低,進一步說明了弱相關影響因素的引入會影響模型預測的準確率。 (1)本研究提出了一種基于BP神經網絡的離港航班滑出時間預測方法,發現了離港航班滑出時間與機場場面交通流有強相關性,與平均滑出時間中度相關,與滑行距離相關性較弱。 (2)基于實際運行數據驗證,考慮強相關和中度相關可量化影響因素的5元組合預測模型的滑出時間預測結果精度最高。引入弱相關的滑出距離后,模型的預測結果精度反而有所降低。 (3)下一步的研究工作將重點放在其它機器學習算法在離港航班滑出時間的預測中的應用。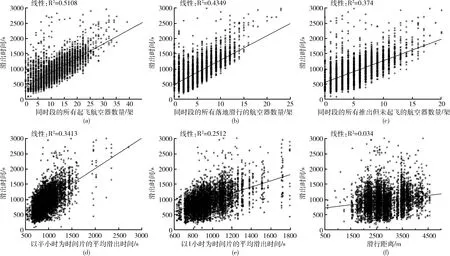
2 滑出時間預測模型
2.1 參數定義
2.2 模型構建

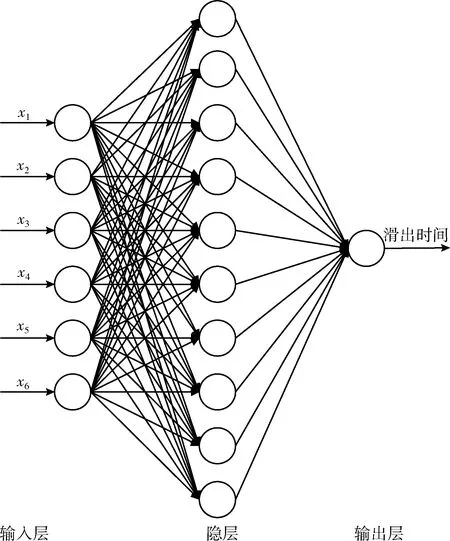
3 基于實際運行數據的離港滑出時間預測
3.1 數據來源

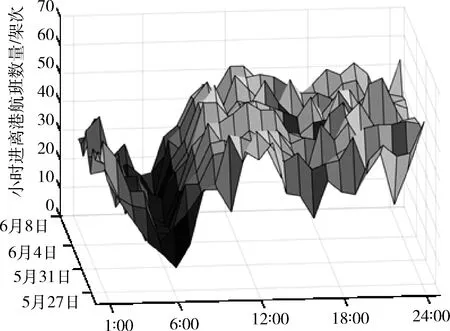
3.2 數據處理
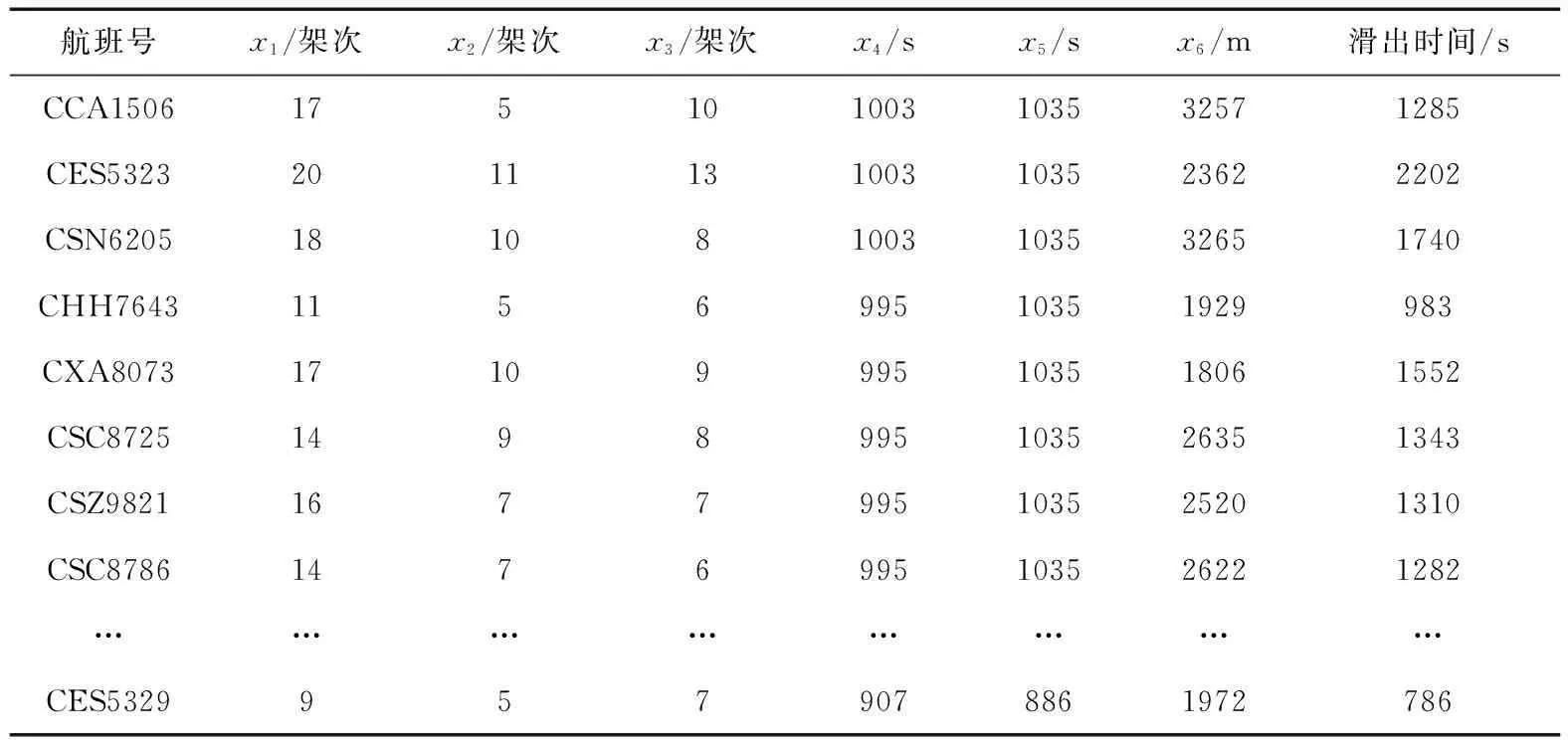
3.3 分析與評價

4 結束語

