基于改進果蠅優化算法的投訴舉報文本分類

范青武，陳 光，楊 凱

(1.北京工業大學 信息學部，北京100124；2.北京工業大學 教育部數字社區工程研究中心，北京 100124；3.北京工業大學 北京城市軌道交通重點實驗室，北京 100124)

0 引 言

通常，投訴舉報受理機構會對舉報信息進行分類，然后根據類別進行派單，所以歸類工作是非常重要的環節，但人工進行歸類會降低工作效率、產生錯誤[1,2]。所以，設計準確高效的投訴舉報信息分類方法成為目前亟待解決的難題。由于文字是投訴舉報信息的主要載體，因此對其進行分類也就是對文本進行分類[3]。

在文本分類問題上，遞歸神經網絡[4]雖然具有較強的學習能力，但其分類精度很大程度上依賴于樣本數量的大小和分布，而投訴舉報文本往往具有樣本數量少、樣本數量分布不均勻等特點，因此這一方法不太適用于此。樸素貝葉斯[5]的分類能力不受樣本數量的大小和分布的影響，但投訴舉報文本通常具有較多的類別特征屬性，這會使樸素貝葉斯的分類性能有所下降。針對以上問題，楊穎等[6]采用融合了Random Subspace技術的支持向量機對投訴舉報文本進行分類，得到了令人滿意的結果。Polpinij J等[7]和Shravan KB等[8]均利用支持向量機進行文本分類，從而克服了由于樣本數量少、樣本數量分布不均勻而造成的分類精度低的問題。Wang Xingkai等[9]通過大量的實驗驗證了支持向量機適用于具有較多類別特征屬性文本的分類問題。由此可見，對于投訴舉報文本分類問題，支持向量機(support vector machine，SVM)表現不俗。可是，很多學者在使用SVM的時候會引入核函數，而核函數參數以及懲罰因子的大小將直接影響其分類精度，如果進行手動調試，不僅費時費力、效率低下，并且準確度不高[10]。對于支持向量機的參數整定問題，實質上屬于一個優化搜索過程，因此采用智能優化算法是最佳選擇[11]。

綜上所述，本文提出一種基于改進果蠅優化算法(improved fruit fly optimization algorithm，IFOA)的文本分類方法，該方法以支持向量機作為文本分類器，同時利用IFOA對分類器參數進行動態尋優，進而構建出IFOA-SVM文本分類模型。

1 果蠅優化算法改進策略

果蠅優化算法(fruit fly optimization algorithm，FOA)是潘文超受到果蠅群體覓食行為的啟發而提出的一種群體智能優化算法[12]。FOA具有結構簡單、計算效率高、易于實現等特點，但其也存在一些缺陷，如搜索半徑固定、種群多樣性低等[13]。因此，本文通過分析FOA的缺陷，針對性地提出了相應的改進方法。

1.1 正切函數編碼法

在FOA當中，種群是由若干果蠅個體所組成的，每只個體都具有一個位置坐標。假設種群當中有4只個體，它們的位置坐標分別是(a,b)、(-a,b)、(a,-b)和(-a,-b)，將其帶入目標函數function并計算個體適應度值fitness，方法如下

(1)

由式(1)可知，這4只個體的適應度值大小是一樣的。如果此時該適應度值是整個種群當中最優的，那么這4只個體所處的位置也就都屬于最優位置。也就是說，整個種群會朝著這4個位置當中的任意一個所處的方向飛行，從而造成位置上的欺騙性。

針對以上問題，對于果蠅個體的位置坐標X，IFOA采用一組角度向量來表示，如下

X=[θ1,θ2,…,θi]

(2)

式中：i表示變量維度，θi表示相位角。由于tan函數在[-π/4,π/4]的范圍內是單調遞增的，并且其值域是[-1,1]，因此θi的取值范圍是[-π/4,π/4]。由此，個體的味道濃度判定值S由式(3)來表示

S=tan(X)

(3)

1.2 雙種群策略

在FOA當中，整個種群會被視為一個整體，種群當中的每只個體都會按照相同的規則進行視覺搜索，這會導致種群整體的搜索能力降低。若此時，目標函數全局最優解的位置比較偏僻或最優個體的位置不理想，那么整個種群可能都會陷入局部最優位置，從而導致算法的最終尋優結果也是局部最優解。

針對以上問題，IFOA在每一次迭代后，會根據個體適應度值的大小將最優位置和最差位置進行記錄，同時計算所有個體與這兩位置間的距離，若其與最優位置距離較近，則將其劃分為搜索能力較強的子群，否則就將其歸到搜索能力較弱的子群當中，同時針對種群的特性分別賦予其不同的搜索策略。

1.3 自適應搜索半徑

由1.2小節已知，IFOA具有兩個小的子群。對于搜索能力較強的子群，搜索半徑應逐步減小，繼而實現在全局最優位置附近進行局部搜索、精確搜索；而針對搜索能力較差的子群，應擴大其搜索范圍，從而增強其全局搜索能力。

綜上所述，為了實現搜索半徑自適應地進行調整，對其進行如下調整

(4)

式中：gi為當前所處的代數，gmax為最大迭代次數，fitnessi為當前個體的適應度值，fitnessi-1為上一代個體的適應度值，Rbest為搜索能力較強的子群的搜索半徑，Rworst為搜索能力較差的子群的搜索半徑，R為初始搜索半徑，m和n均為自適應半徑的參數，i為迭代次數。

2 IFOA-SVM文本分類方法

基于IFOA-SVM的投訴舉報文本分類方法由文本預處理、SVM分類模型構建以及模型的參數尋優這3個部分組成，具體步驟如圖1所示。

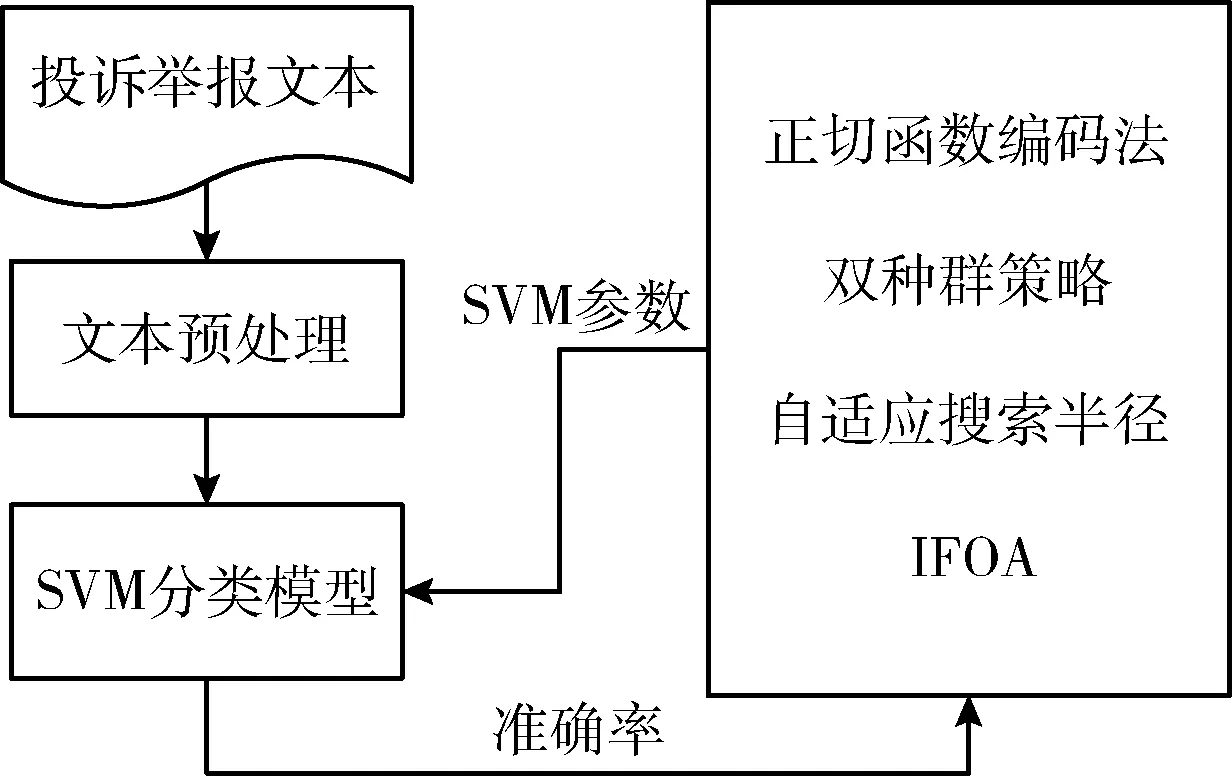
圖1 基于IFOA的投訴舉報文本分類步驟

2.1 文本預處理

對投訴舉報文本進行預處理的步驟由詞語切分、去除停用詞、文本表示以及特征提取組成。

首先，對于投訴舉報文本的詞語切分，本文采用python中的分詞工具包jieba。

其次，本文利用復旦大學停用詞表來去除投訴舉報文本中的停用詞。

然后，針對投訴舉報文本表示，本文采用向量空間模型(vector space model，VSM)法。VSM是由Salton等[14]于20世紀70年代末提出的，是一種簡便、高效的文本表示方法，其表達式如下

Di=D(t1,w1;t2,w2;…;tn,wn)

(5)

式中：Di為某條投訴舉報文本的空間向量，i為文本的編號，tn為投訴舉報文本當中某個詞語所對應的子向量，wn為子向量的權重，n為子向量的標號。

此外，為了進一步突出文本的特征、降低詞向量的維度，本文采取詞頻-逆向文檔頻率(term frequency-inverse document frequency，TF-IDF)算法對文本模型進行特征提取。TF-IDF由G.Salton等提出[15]，其計算方法如式(6)所示

Pi=tfij·idfi

(6)

式中：Pi為每一個詞語的綜合頻度，tfij為某個詞語在一篇文檔中出現的頻率，idfi為包含某個詞語的文檔占整個文本集的比例，i為詞語的標號，j為文檔的標號。

經過特征提取后，投訴舉報文本就被表示成經過降維的詞向量，如式(7)所示

D’i=D’(t1,w1;t2,w2;…;tq,wq)

(7)

式中：D’i為某條投訴舉報文本所對應的降維空間向量，i為文本的編號，tq為投訴舉報文本當中某個詞語所對應的子向量，wq為子向量的權重，q為子向量的標號。此時，q的值小于式(5)當中n的大小。

2.2 SVM文本分類模型

SVM是學者Vapnik提出的一種機器學習方法，因其對小樣本、高維度、非線性等分類問題具有良好的學習和泛化能力而被廣泛應用[16]。

假設一組給定的投訴舉報文本集，其所對應的降維向量x的表達式如下

x={(x1,y1),(x2,y2),…,(xn,yn)}

(8)

式中：xn為某條投訴舉報文本所對應的降維空間向量，yn為該條文本所對應的類別，n為文本的編號。

SVM利用最優超平面來區分投訴舉報文本的類別，其滿足條件如下

wT·x+b=0

(9)

式中：w為超平面的法向量，wT為法向量的轉置向量，b為偏移量。

yi·[w·xi+b]≥1,i=1,2,…,n

(10)

式中：i為子向量的標號。

因此，引入Lagrange函數，將以上問題轉化為求解對偶問題。由此，得到超平面函數l(x)，如下所示

(11)

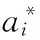
可是，如果此時投訴舉報文本屬于線性不可分類的對象，那么線性分類器將陷入無限循環。此時，引入核函數，將輸入的詞向量映射到一個高維的Hilbert空間當中。

由于高斯徑向基函數(radial basis function，RBF)具有較強的映射能力[17]，故本文選取RBF作為SVM的核函數，如式(12)所示

(12)

式中：σ為RBF的寬度參數。

引入了RBF后，空間向量仍存在一些線性不可分的部分。因此，引入松弛變量ei，從而使約束條件轉化為下式

[w·xi+b]-1+ei≥0,i=1,2,…,n

(13)

此外，為了控制SVM的整體錯誤率，引入懲罰因子C，從而轉化為在式(13)的約束下求解下式的最小值

(14)

以上步驟是SVM構造一個用于對兩個類別的投訴舉報文本進行分類的分類面，但投訴舉報文本的類別數目卻遠不止兩類，因此采取一對多(one-against-rest)的分類策略，即對于類別數目為n的投訴舉報文本集，構造n個分類面。

2.3 SVM參數尋優

通過2.2小節的論述可以得知，找到參數C與σ的最優值是實現精確分類的關鍵所在。Wang Qing等[18]采用蟻群算法對SVM的參數進行動態尋優；陳志珍[19]利用粒子群算法動態優化SVM的參數。但以上文獻也分別指出，蟻群算法和粒子群算法容易陷入目標問題的局部最優解。林濤等[20]利用經過改進的FOA對SVM的參數進行動態優化，從而提高了SVM的分類精度；王巖等[21]和Luo Shiyu等[22]也通過大量的實驗驗證了FOA在動態優化SVM的參數方面具有較強的收斂能力。然而，以上文獻也均提到了FOA存在一定的缺陷。綜上分析，本文利用IFOA對SVM的參數進行動態尋優。

利用IFOA對SVM參數進行動態尋優的步驟如下：

(1)初始化IFOA的參數，包括種群規模p、最大迭代次數gmax、初始搜索半徑R、變量維度、自適應半徑參數m和n。隨機生成每一只果蠅個體的初始相位角坐標X，由于此時需要對兩個參數進行尋優，因此X的形式為一個p行2列的數組，如式(15)所示

(15)

式中：rand為大小在0至1之間的隨機數。

(2)計算所有果蠅個體的味道濃度判定值S，此時S的形式同樣為一個p行2列的數組，如式(16)所示

(16)

(3)將每一只果蠅個體的味道濃度判定值S當中的兩個元素分別作為C和σ，依次輸入至SVM分類模型當中，同時利用測試文本集對模型進行分類測試。此時，IFOA的目標函數是以C和σ為自變量的分類準確率函數，如下式所示

(17)

式中：P(C,σ)為輸入參數大小分別為C與σ的情況下的分類準確率，TP為SVM分類模型在輸入參數大小分別為C與σ的情況下預測結果為c類，并且實際屬于c類的文本數量；FP為SVM分類模型在輸入參數大小分別為C與σ的情況下預測結果為c類，但實際不屬于c類的文本數量。

(4)使用準確率函數計算出SVM分類模型的分類準確率，作為果蠅個體的適應度值fitness，如式(18)所示。之后，挑選出整個種群當中適應度值最大以及最小的個體，分別作為最優個體和最差個體，記錄其位置以及適應度值

fitness=P(C,σ)

(18)

(5)計算所有果蠅個體與最優個體和最差個體間的距離，若其與最優個體間的距離比最差個體間的距離近，則將其劃分為搜索能力較強的子群，否則將其劃分為搜索能力較差的子群

(19)

式中：distancebest為其它個體與最優個體間的距離，X(best,1)與X(best,2)為最優個體的位置，distanceworst為其它個體與最差個體間的距離，X(worst,1)與X(worst,2)為最差個體的位置。

(6)搜索能力較強和搜索能力較差的果蠅子群分別按照不同的半徑在最優個體的指導下進行視覺搜索，更新位置

(20)

(21)

上面幾個式子中，Xbest(p,1)與Xbest(p,2)為搜索能力較強的子群當中個體的位置坐標，Rbest為搜索能力較強的子群的搜索半徑，Xworst(p,1)與Xworst(p,2)為搜索能力較差的子群當中個體的位置坐標，Rworst為搜索能力較差的子群的搜索半徑。

(7)計算位置更新后果蠅個體的味道濃度判定值，同樣將其中的兩個元素分別作為C和σ，依次輸入SVM分類模型當中，同時再次利用測試文本集對模型進行分類測試，計算出分類準確率，作為新的個體適應度值。最后，記錄新的最優和最差個體的位置及適應度值，若該最優個體的適應度值小于上一代的，則最優個體的位置以及最優的適應度值仍延用上一代的。

(8)進入算法的迭代過程，重復步驟(2)至步驟(7)，若達到最大迭代次數，則算法結束，輸出末代最優個體的味道濃度判定值，分別作為最佳的C和σ。

翻轉課堂譯自“Flipped Classroom”或“Inverted Classroom”，也可譯為“顛倒課堂”，是指重新調整課堂內外的時間，將學習的決定權從教師轉移給學生。在這種教學模式下，課堂內的寶貴時間，學生能夠更專注于主動的基于項目的學習，共同研究解決本地化或全球化的挑戰以及其他現實世界面臨的問題，從而獲得更深層次的理解。教師不再占用課堂的時間來講授信息，這些信息需要學生在課前完成自主學習，他們可以看視頻講座、聽播客、閱讀功能增強的電子書，還能在網絡上與別的同學討論，能在任何時候去查閱需要的材料。教師也能有更多的時間與每個人交流。

3 實驗與分析

3.1 標準語料庫分類實驗

3.1.1 實驗方法

為了探究本文方法的分類效果，本文采用復旦大學語料庫[23]作為文本分類實驗對象，對該方法進行驗證，選取其中最具有代表性的5個類別的文本，即Space、Art、Environment、Politics和Sports，其中每個類別的文本數量均為150篇。

此外，本文還選取了果蠅優化算法優化支持向量機參數(FOA-SVM)、粒子群算法優化支持向量機參數(par-ticle swarm optimization-SVM，PSO-SVM)、天牛須搜索算法[24]優化支持向量機參數(beetle antennae search-SVM，BAS-SVM)以及其它幾種常見的未經過參數優化的傳統機器學習方法，即SVM、邏輯回歸(logistic regressive，LR)、K最近鄰(k-nearest neighbor，KNN)、樸素貝葉斯(naive Bayesian，NB)和隨機森林(random forest，RF)作為對比。其中，FOA與IFOA的種群規模均為20、最大迭代次數均為200、初始搜索半徑均為2，變量維度均為2，同時IFOA的自適應半徑參數m和n分別為16與32；PSO的種群規模為20、最大迭代次數為200、學習因子均為1.5、變量維度為2、搜索范圍在0到2之間；BAS的天牛步長為1、變步長參數為0.95、常數c為5、變量維度為2。其它幾種傳統的機器學習方法均直接采用python軟件當中機器學習工具包的默認參數。

對于訓練文本集和測試文本集的劃分，為了消除方法所具有的隨機性，本文采取5折交叉驗證法，將每個類別的文本平均分成5份，隨機選取4份作為訓練文本集，1份作為測試文本集，因此每一種文本分類方法都將進行5次獨立重復實驗，最終結果以這5次實驗的平均值為準。

實驗PC機所用的操作系統為Windows 10，處理器為Inter(R)Core(TM)i5-5200U @ 2.2 GHz，內存為4 GB。

3.1.2 評價指標

對于優化算法性能的評價標準，本文采用實驗結果的平均值，也就是優化算法最優解的平均值。實際上，就最優解而言，其值的大小也就是最優參數下SVM分類模型的分類準確率。因此，目標函數優化結果的平均值越接近1，說明SVM分類模型在最優參數下的分類準確率越高，從而可以驗證優化算法的尋優精度也就越高。

對于文本分類結果的評價標準，常用的指標主要有3個，即準確率、召回率和F(F-measure)值[25]。假設TP為預測結果為c類，實際屬于c類的文本數量；FP為預測結果為c類，實際不屬于c類的文本數量；TN為預測結果不為c類，實際不屬于c類的文本數量；FN為預測結果不為c類，實際屬于c類的文本數量。

(22)

式中：P代表準確率的大小。

召回率表示整個對象集當中所含指定類別的對象占實際目標類中對象的比例(百分比)，其計算方法如下

(23)

式中：R代表召回率的大小。

F值則代表準確率與召回率的調和均值，其計算方法如下

(24)

由于準確率和召回率是文本分類精度的最直接體現[26]，因此本實驗采用準確率和召回率來衡量文本分類的效果。

3.1.3 實驗結果

表1為復旦大學語料庫分類實驗的優化算法性能；表2、表3分別為復旦大學語料庫分類實驗的準確率和召回率的大小。

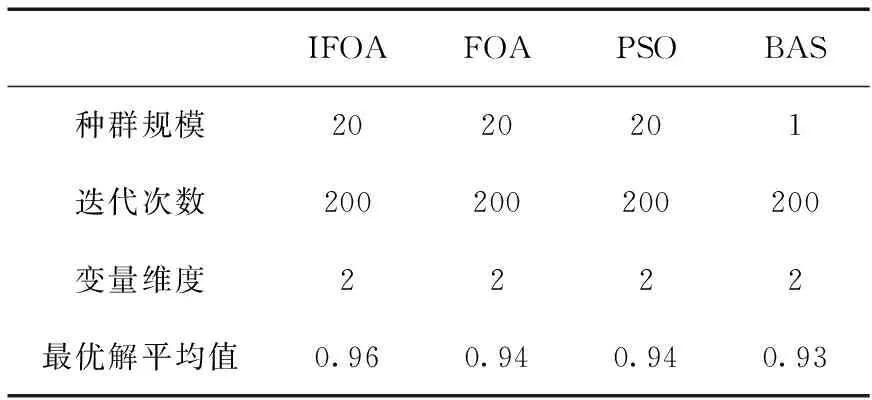
表1 復旦大學語料庫分類實驗優化算法性能

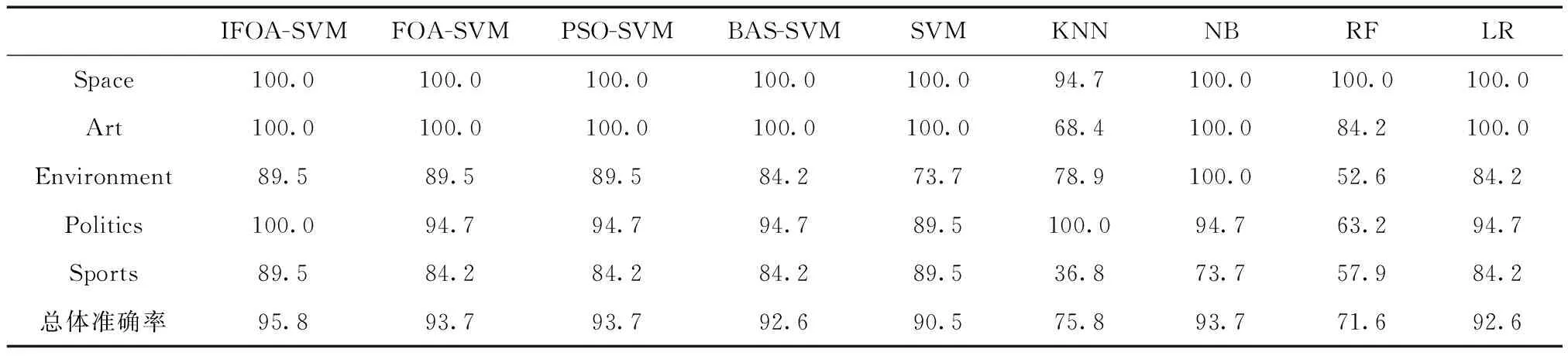
表2 復旦大學語料庫分類實驗準確率/%

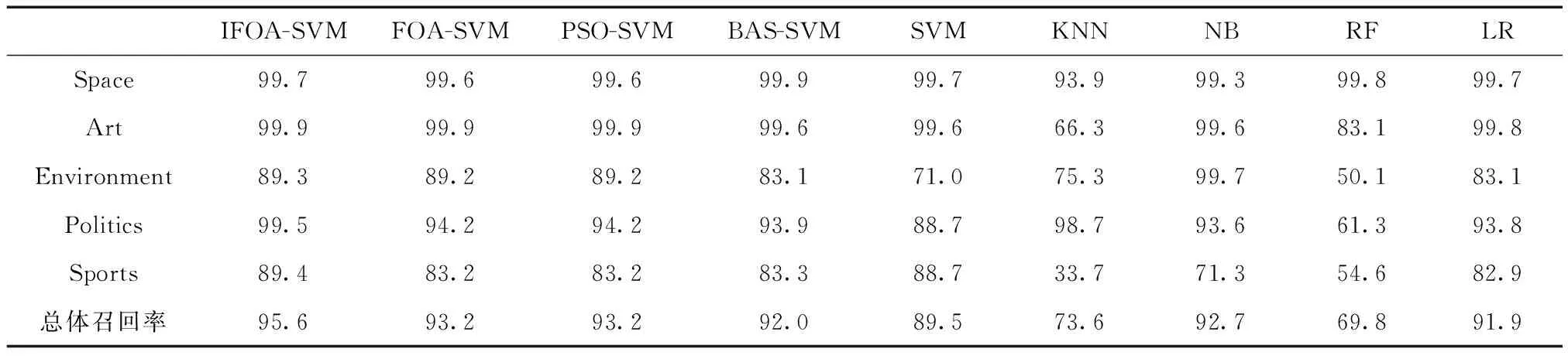
表3 復旦大學語料庫分類實驗召回率/%

3.1.4 結果分析

首先通過觀察表1中的數據，可以得知在4種優化算法的最優解平均值當中，IFOA的結果達到了0.96，相比于FOA、PSO和BAS的而言更加地接近1。由此可見，對于標準語料庫分類實驗，IFOA在動態優化SVM參數方面具有更強的收斂能力。

其次，通過表2和表3可以直觀地看出，相比于其它的文本分類方法而言，IFOA-SVM在每個類別文本分類的準確率和召回率上均是最高的，同時其整體的分類準確率和召回率也都是最高的。因此，對于標準語料庫分類實驗，IFOA-SVM具有較強的分類能力。

3.2 投訴舉報文本分類實驗

3.2.1 數據說明

本文依托某大型環境污染投訴舉報平臺，經過去重合并、去除無意義條目后，從中獲取了4000余條有效的投訴舉報文本，其數量分布情況見表4。之后，由經過嚴格培訓的專業人員根據環保部于2017年發布的污染源類型名稱表對每一條投訴舉報文本進行人工標注，同時對標注結果進行一致性檢驗。

表4 投訴舉報文本數量分布

3.2.2 實驗設計

對于投訴舉報文本的分類實驗，實驗方法、算法的參數設置、所選取的對比方法以及PC機的型號均與3.1.1小節當中所描述的完全一致。

3.2.3 評價指標

對于優化算法性能的評價標準，本實驗仍然采用優化算法最優解的平均值。對于投訴舉報文本分類實驗的評價標準，本實驗則同樣采用文本分類結果的準確率和召回率。

3.2.4 實驗結果

表5為投訴舉報文本分類實驗的優化算法性能；表6、表7分別為投訴舉報文本分類實驗的準確率和召回率。

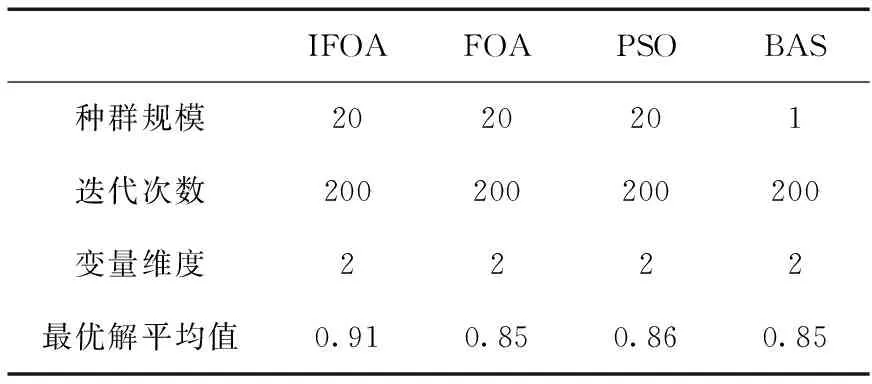
表5 投訴舉報文本分類實驗優化算法性能

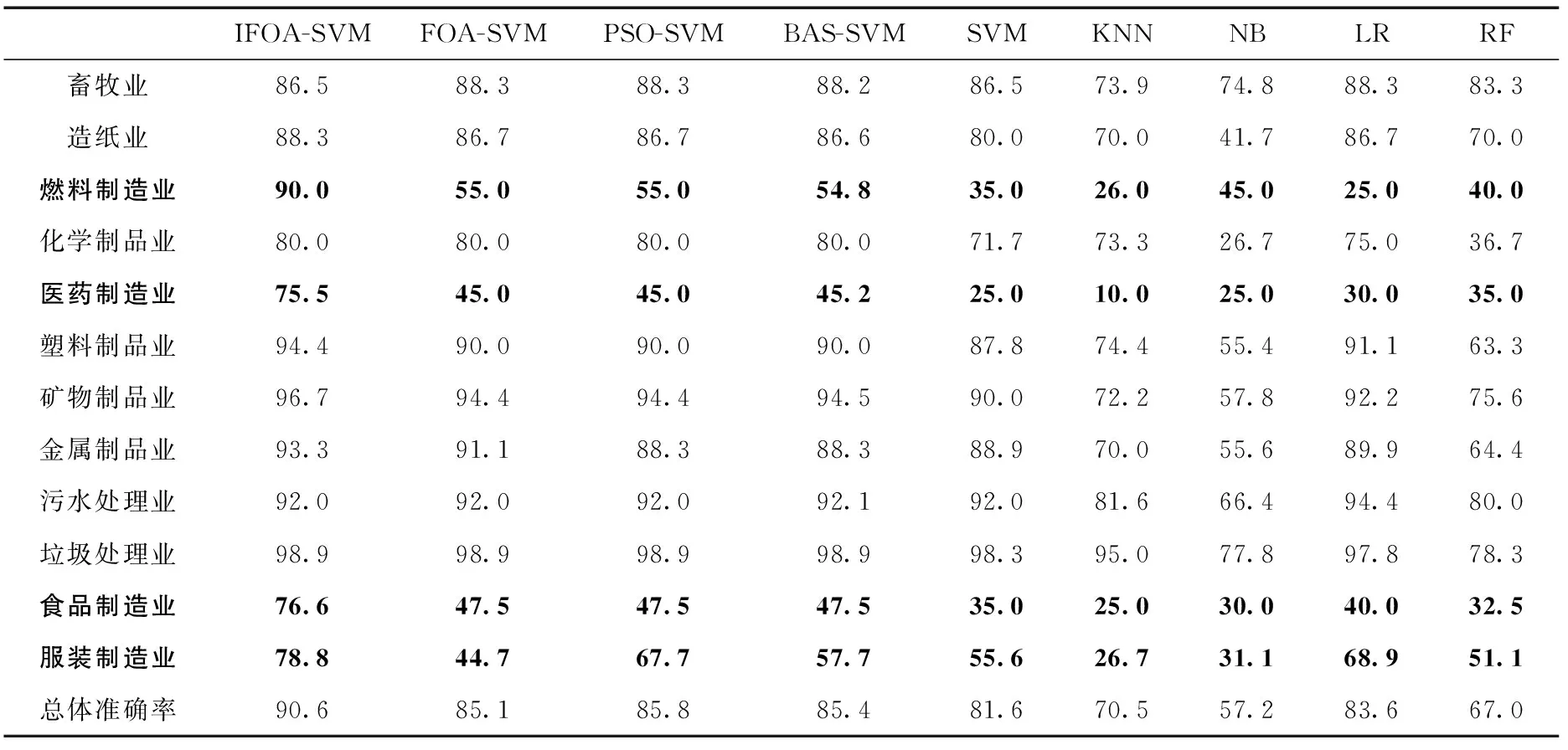
表6 投訴舉報文本分類實驗準確率/%

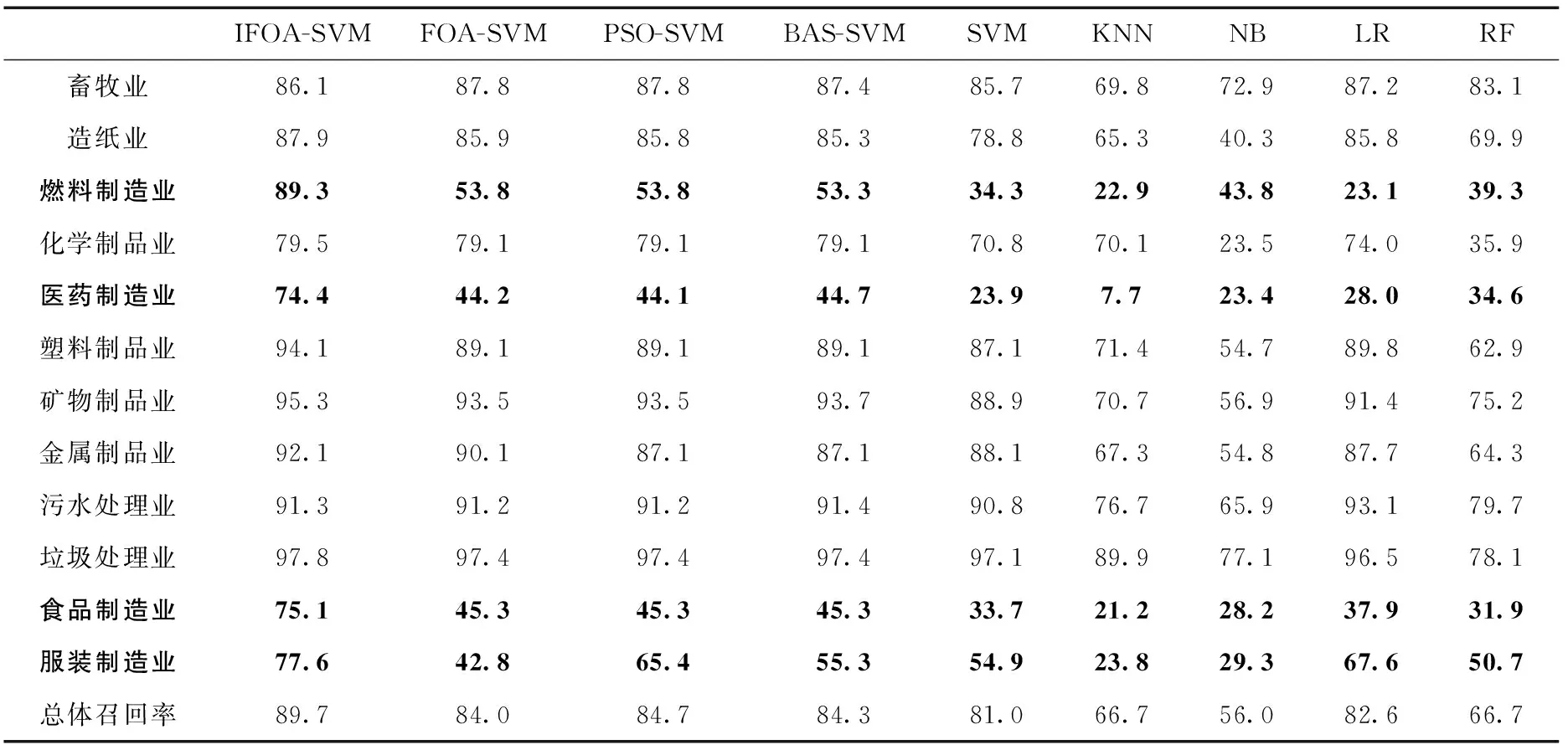
表7 投訴舉報文本分類實驗召回率/%

3.2.5 結果分析

首先，從表5當中可以得知，在4種優化算法的最優解平均值當中，IFOA的結果達到了0.91，相比較于其它3種優化算法而言更加地接近1，由此驗證了對于投訴舉報文本分類實驗，IFOA在優化SVM參數方面同樣具有較強的收斂能力。

其次，通過表6和表7我們可以清晰地觀察到，相比于其它的文本分類方法，IFOA-SVM除了在畜牧業和污水處理業這兩類投訴舉報文本的分類準確率和召回率上略微遜色以外，在其它類別文本上的分類結果均是最好的，同時其整體的分類準確率和召回率也都是最高的。其中，針對燃料制造業、醫藥制造業、食品制造業和服裝制造業這4類極難正確分類的投訴舉報文本，其它幾種分類方法的準確率和召回率都很低，有的甚至只有10%，可以說另外那90%的文本都歸到了錯誤的類別，而IFOA-SVM的卻全都超過了75%，有非常顯著的提高。

實際上，通過表4當中的數據可以得知，對于燃料制造業、醫藥制造業、食品制造業和服裝制造業這4類投訴舉報文本，它們的樣本數量相比與其它類別的文本而言普遍很少，所以在對其進行分類的時候非常容易把它們錯誤地歸到樣本數量多的類別當中，而IFOA-SVM卻依然能保持一定的分類準確率和召回率。

綜上，對于投訴舉報文本分類實驗，IFOA-SVM不僅僅具有較高的分類準確率和召回率，其適應性與泛化能力也極強。

4 結束語

投訴舉報文本具有長度短、類別特征不明顯、樣本數量少且分布不均衡等特點。因此，利用傳統的機器學習方法對其進行分類會產生精度低等問題。由此，本文提出了一種基于IFOA-SVM的文本分類方法，即利用IFOA來對SVM的參數進行動態尋優，以此來提高SVM的分類精度。

文本分類實驗結果表明，IFOA的尋優能力相比于FOA而言的確有所提高，并且IFOA-SVM方法相比于其它幾種常見的文本分類方法而言具有更高的分類準確率和召回率，可以滿足實際需求，適用于投訴舉報文本分類這一問題。

對于投訴舉報文本分類問題，文本的預處理對于其分類精度也是至關重要的。因此，本文的下一步工作將聚焦于文本的預處理方法，通過對方法的改進來進一步提高文本分類的精度。