山區高墩雙塔斜拉橋約束體系研究
黃永福HUANG Yong-fu;李杰LI Jie;鄒惠瓊ZOU Hui-qiong;尹開川YIN Kai-chuan
(云南省交通規劃設計研究院有限公司,昆明 650041)
0 引言
我國西部多為山區,地形地勢復雜,地震烈度較高,給修建跨越山谷河流的橋梁建設帶來較大的技術難題和施工風險。隨著“一帶一路”發展戰略的推進和深入,西部地區作為陸上絲綢之路的必經之地,必須加速基礎設施建設,帶動地區社會經濟,以適應國家發展戰略。
斜拉橋作為典型的索結構橋梁,在200m~1000m跨度范圍內具有較好的經濟性。山區斜拉橋跨越深山峽谷,往往具有塔高和墩高的特點,導致結構的整體剛度小、主梁重心相對于墩底較高,給斜拉橋整體穩定性、抗震性能帶來了極為不利的影響,如何提高整體剛度并減小結構地震響應關系著橋梁結構的安全。通過加大索塔截面尺寸,可以有限地增加整體剛度,一定程度上解決了穩定性問題,但帶來的是建設成本的大幅上升和結構地震內力的增大,降低結構安全性。大量研究表明[1]~[4],選擇合理適用的斜拉橋約束體系,是改善高塔斜拉橋穩定性、抗震性能最為直接和有效的措施。
斜拉橋常用的約束體系有[5]:①全漂浮體系,即索塔與主梁之間無任何約束裝置;②半漂浮體系,索塔與主梁之間設置豎向支承,在縱橋向為自由狀態;③固結體系,或稱剛構體系,即塔墩梁固結;④支承體系,即塔梁固結,并支承于橋墩上。中等及大跨度斜拉橋多采用全漂浮體系或半漂浮體系,但由于山區斜拉橋墩高、結構柔的特點,這幾種常規約束體系不能較好地滿足大跨度斜拉橋的設計要求。
以一座典型山區高墩雙塔斜拉橋為例,在常規約束體系的基礎上,提出彈性約束體系,與半漂浮體系、單塔固定體系、雙塔固定體系對比,通過結構穩定性能、抗震性能分析,驗證彈性約束體系的合理性,為高塔斜拉橋約束體系選擇提供參考。
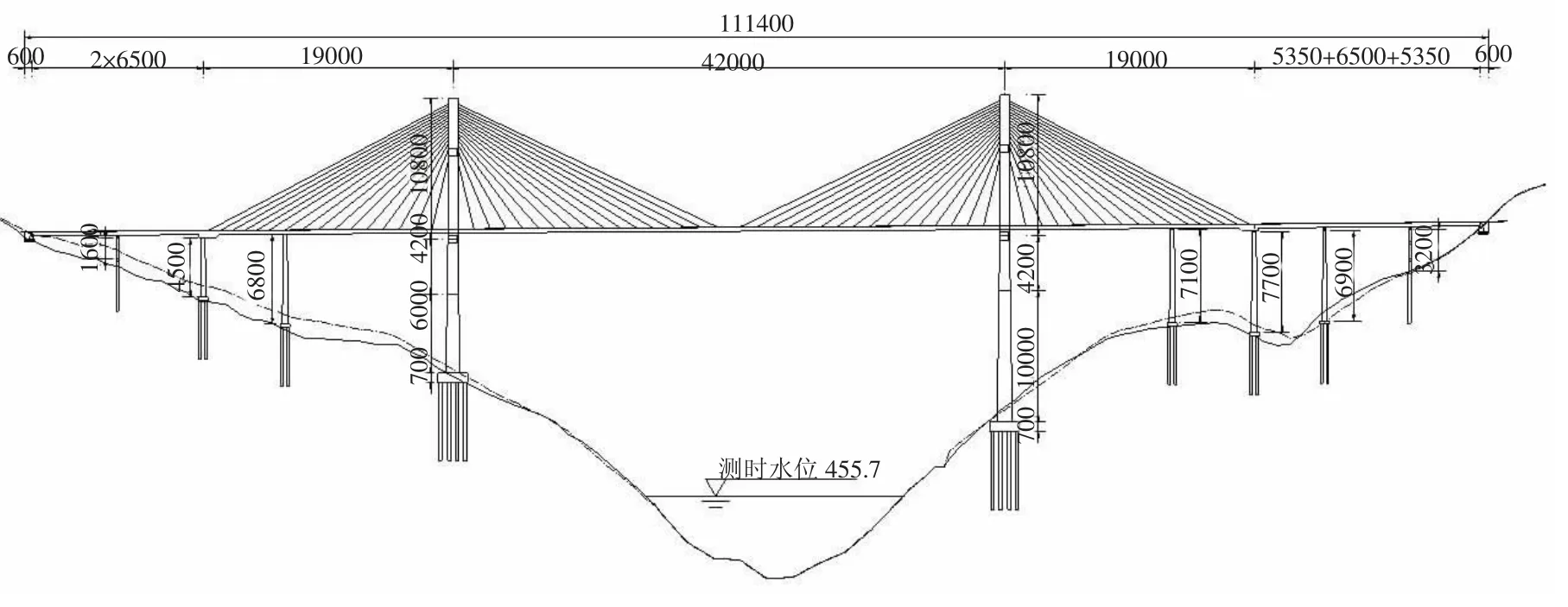
圖1雙塔斜拉橋總體布置圖(cm)
1 工程案例
該雙塔斜拉橋主橋為(190+420+190)m雙塔三跨鋼混組合梁斜拉橋[6],邊跨設置輔助墩,跨徑組合為(62.4+127.6)m。主梁為由工字型鋼縱梁、橫梁、小縱梁、混凝土橋面板及連接件組成的格構式鋼混組合梁,主梁全寬29m;斜拉索為扇形平行雙索面,索面間距為26.5m,標準拉索間距為12.4m;索塔采用花瓶形索塔,由上塔柱、中塔柱、下塔柱、塔墩、上橫梁、下橫梁和群樁基礎組成,兩岸索塔高度分別為210m和250m。橋梁總體布置如圖1所示。
為了綜合評價半漂浮體系、單塔固定體系、雙塔固定體系、彈性約束體系四種體系對于高塔斜拉橋受力的優劣,將從結構穩定性、抗震性能兩個方面進行闡述與論證。
2 結構穩定性分析
斜拉橋的索塔、主梁承受著巨大的軸力和彎矩,在施工階段和運營階段可能出現失穩現象,穩定問題可分為第一類穩定(彈性穩定)和第二類穩定(非線性穩定),彈性穩定可以作為結構穩定性的初步評估。
彈性穩定是一種理想情況,當結構承受臨界荷載時,若收到微小擾動,結構將喪失穩定,可能進入新的平衡狀態。根據最小勢能原理,彈性穩定在數學上可用以下平衡方程來表達:
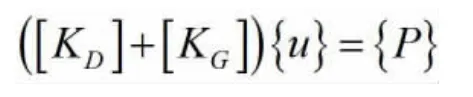
式中,[KD]為結構彈性剛度矩陣,[KG]為結構幾何剛度矩陣,{u}為位移矩陣,{P}為荷載矩陣;當荷載達到臨界荷載λ{P}時,幾何剛度矩陣也增大λ倍,在微小擾動{△u}下,即便荷載λ{P}保持不變,仍然可保持臨界平衡狀態,于即有
因此,臨界荷載系數λ在數學上變為求解特征值問題。
采用SAP2000有限元程序,建立空間計算模型,主梁、索塔、橋墩均采用梁單元模擬,斜拉索采用僅受拉桁架單元模擬;考慮成橋索力、主梁軸力、索塔軸力對結構剛度的影響(P-Delta效應);承臺近似按剛體模擬,其質量堆聚在承臺質心,承臺底部固結;主梁壓重、加勁肋等重量及二期恒載以點質量或線質量形式施加在主梁上;彈性約束兩端錨固在主梁和索塔橫梁上,單個索塔的彈性約束剛度取2×104kN/m,支座均按實際的固定或滑動模擬。四種約束體系彈性穩定分析結果如表1所示。
由表1結果可知,半飄浮體系縱向無約束,彈性穩定系數僅為4.58,雖然可以滿足設計規范最小值4.0的要求,但結構剛度低,穩定性差,安全富余度太小;單塔固定、雙塔固定或設置彈性約束后,彈性穩定系數有了明顯的提升,對縱向剛度有較大的影響,能很好地滿足設計規范要求。對于山區高墩雙塔斜拉橋,建議采取縱向約束措施,提高橋梁整體穩定性能。
3 抗震性能分析
橋位區地震烈度為Ⅶ度,地震動加速度峰值為0.15g,場地類別為Ⅱ類。根據本橋場地地震安全性評價報告[7],主橋工程場地水平地震動參數見表2。
表2中,T1為設計反應譜第一拐點周期,T2為設計反應譜第二拐點周期,βmax為動力放大系數反應譜平臺值,γ為設計反應譜下降段衰減指數,Cs為阻尼調整系數,Cd為場地系數,Amax為峰值加速度。
首先進行動力特性分析。采用Litz向量法進行特征值分析,取前300階振型,通過計算,振型累積貢獻系數達到99%以上。表3列出了各約束體系的前10階振型的動力特性。
從表3中可以看出,由于四種體系在縱橋向采取了不同的約束方式,其動力特性主要的區別也表現在縱橋向。第一階振型均為縱飄,半飄浮體系一階周期為11.55s,為四種約束體系中最大值,因此結構剛度最小;雙塔固定體系一階周期為4.51s,為四種約束體系中最小值,因此結構剛度最大;彈性約束體系和單塔固定體系介于以上二者之間。
采用反應譜分析方法[8],振型組合采用CQC,方向組合采用SRSS,得到四種體系在50年2%概率水準下的地震響應。
從圖2可知,雙塔固定時,1號索塔剪力遠大于其他工況,塔墩底達到1.68倍,塔柱底達到2.55倍,對1號索塔截面抗剪承載力要求大大提高;單塔固定時,2號索塔(即固定約束的索塔)索塔剪力遠大于其他工況,塔墩底達到1.43倍,塔柱底達到2.17倍,對2號索塔截面抗剪承載力要求大大提高;彈性約束體系索塔內力比半飄浮體系大4%~17%,因此該彈性約束的設置對索塔內力影響較小,認為在可接受的范圍內。

表1各約束體系穩定系數

表2工程場地水平地震動參數
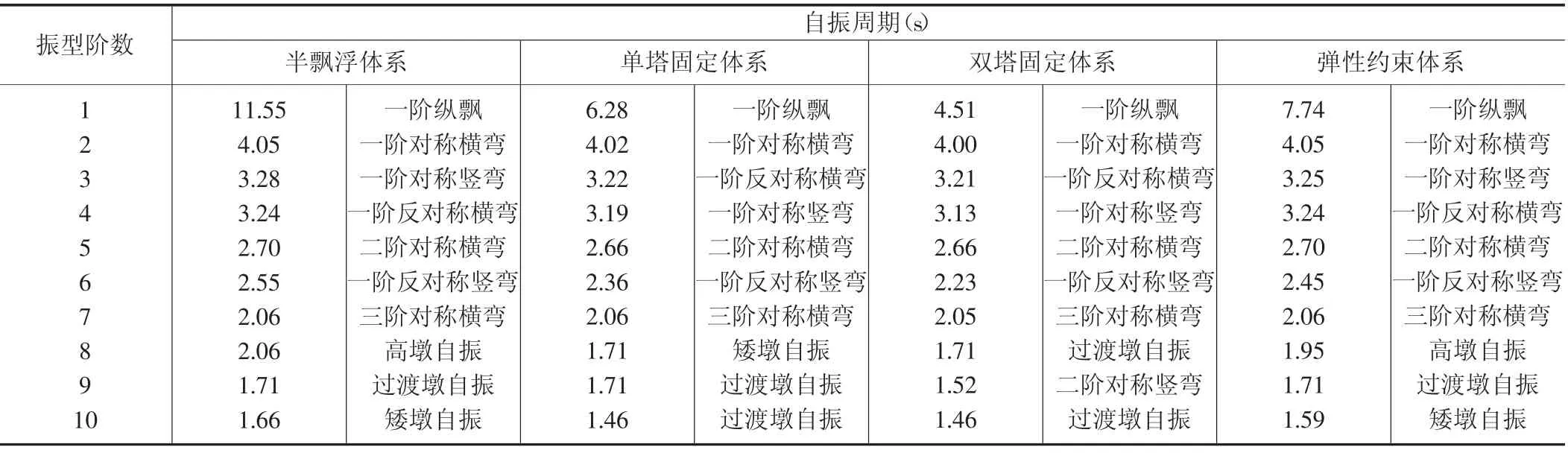
表3各約束體系動力特性

圖2各約束體系索塔縱向剪力
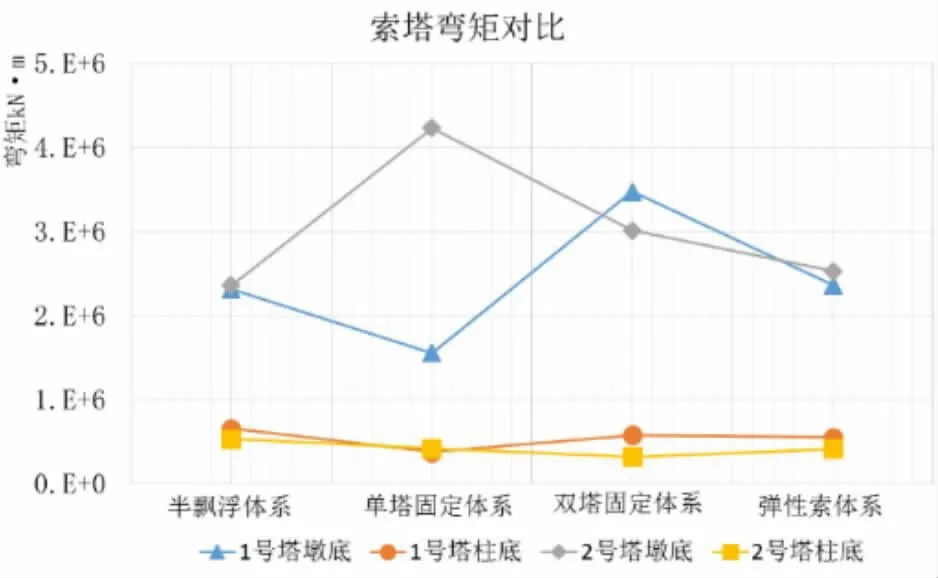
圖3各約束體系索塔縱向彎矩
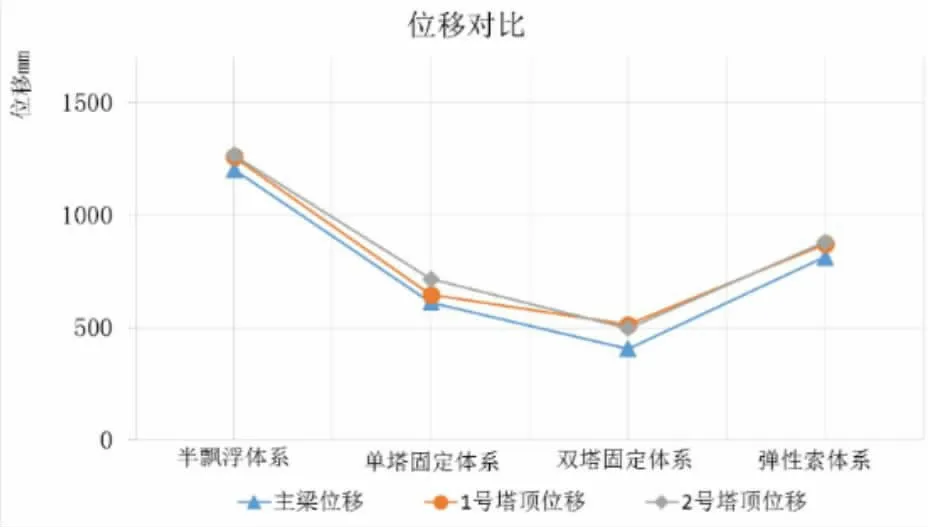
圖4各約束體系索塔縱向彎矩
從圖3可知,雙塔固定時,1號索塔彎矩遠大于其他工況,塔墩底達到2.23倍,塔柱底達到1.54倍,對1號索塔截面抗彎承載力要求大大提高;單塔固定時,2號索塔(即固定約束的索塔)索塔彎矩遠大于其他工況,塔墩底達到1.79倍,塔柱底達到1.3倍,對2號索塔截面抗剪承載力要求大大提高;彈性約束體系索塔塔墩底內力與半飄浮體系基本相當,但塔柱彎矩減小了16%~22%。彈性約束將塔頂一部分地震力下放至塔梁交界處,減小了地震力傳遞的力臂,因此彎矩可能降低,實際分析結果與定性分析結論基本一致。總體而言,該彈性約束的設置對索塔抗彎計算有利。
從圖4可知,雙塔斜拉橋塔頂位移與主梁位移基本相當。半飄浮體系由于未設置縱向約束,塔和梁的縱向位移最大,達到雙塔固定體系的3倍,為彈性約束體系的1.48倍,從結構動力特性分析也可推斷出這一趨勢。
此外,由于后三種體系設置了縱向約束,約束裝置上將產生水平地震約束力。根據計算結果,單塔固定約束縱向剪力為19200kN,雙塔固定約束縱向剪力為18850kN,彈性約束縱向力為5470kN。無論是單塔固定還是雙塔固定,塔梁之間均產生了非常大的水平約束力,目前支座等裝置的水平承載力很難滿足受力需要,其次巨大的地震力將導致主梁鋼結構及索塔橫梁產生局部破壞,從而使得約束體系失效。
綜上所述,單塔固定還是雙塔固定產生了較大的索塔內力及約束裝置地震力,實際工程中難以克服,因此均不是合理的約束體系;半飄浮體系在索塔內力方面表現良好,但產生了較大的縱向位移,梁端需設置大型伸縮縫,加上伸縮縫壽命較短,造價較高,后期維護成本不菲;而彈性約束既保證了索塔內力較優,又限制了梁端過大的位移,實現了力與位移的平衡。因此從結構抗震的角度,設置彈性約束是受力合理、經濟性好的選擇。
4 結語
通過結構穩定性能分析及抗震性能分析,設置縱向彈性約束有效地提高了橋梁整體穩定性能,提升了結構抗震性能,是山區高墩雙塔斜拉橋結構體系的合理解決方案。

