基于改進遺傳算法的混流手機殼產線動態平衡研究

顏家新YAN Jia-xin；黃麗HUANG Li

（①攀枝花學院智能制造學院，攀枝花 617000；②攀枝花學院經濟與管理學院，攀枝花 617000）

0 引言

個性化的購買趨勢使傳統高度自動化的生產模式難以適應市場需求，促使制造企業選擇多品種、小批量的柔性生產方式。然而，柔性化的生產模式會增加生產系統的組織、調度和最優控制的難度，如果不能制定合理的生產作業計劃，則會導致生產效率低下，難以保證交貨期[1]，將會嚴重影響企業效益。因此，混流制造系統調度問題的研究和探索十分必要。

混流裝配線投產排序是通過滿足某些約束條件來解決一些復雜組合優化問題，是柔性制造系統中排序的一種典型問題。投產排序的目的是通過根據不同產品訂單的工藝路線或交貨時間從而合理制定分配資源、優化性能指標為企業制定出最優的投產排序方案，從而為企業帶來最低的生產成本和最高的經濟效益。因此，設計出能夠適應市場內外環境變化、持續保持動態平衡的裝配線，已成為現代企業急不可待的需求之一。

學者楊武成[2]針對第一類混流裝配線平衡問題，兼顧工作站數、工人數和工作站負荷均衡，引入了新變量和不對稱約束來構建新的數學模型。提出了一種改進的雞群算法求解，研究結果表明：在算例驗證中，對比傳統的模型，新模型多找出8 個算例的最優解，且尋優速度更快。

學者劉禹[3]針對現有生產平衡技術中研究較少的第二類生產線平衡問題，將工業工程方法與改進遺傳算法相結合，提出一種用改進遺傳算法來分析、解決生產線平衡問題的方法技術，并把這種方法應用到實際生產線平衡問題的改善上，取得了較好的效果。

學者張曉文[4]針對初始生產線平衡的串-并聯生產系統，采用可靠度恢復因子描述設備維護前后的可靠度演變，建立了一種基于可靠度的以總成本最小為優化目標的串-并聯生產系統機會維護模型，采用蒙特卡洛仿真的方法獲得最優的預防性維護和機會維護的閾值，從而得到滿意的維護計劃。

在裝配線的動態平衡問題中考慮串-并聯生產系統的研究很少，而本文的研究又為裝配線的動態平衡問題提供了考慮串-并聯生產系統的新方向。本文針對混流裝配線串-并聯生產系統的多目標優化問題，建立了以降低生產節拍和工作站負荷為目標的優化模型，運用了雙種群遺傳算法的模型求解方法，實現了針對生產線生產節拍和工作站負荷的優化目標。

1 案例分析與改善

1.1 問題描述

成都J 有限公司手機殼裝配線為研究對象，該公司的總裝線為一條混流生產線，在該總裝線上裝配型號A、B、C 為三種結構相似的手機殼。公司每天兩個班次，每個班次的有效工作時間為8H；手機殼的每日計劃總產量為2500 件，其中，手機殼三種型號的計劃產量為A:B:C=1000:1000:500。各工作站作業任務和串并聯關系見表1，各工作站產品作業時間見圖1。

表1 各工作站作業任務和串并聯關系

其中，手機殼裝配線初始平衡的有效工作時間T=2×8×3600=57600s；日需求Dq=2500 件；K=16 個工作站，每個工作站的作業時間見圖，根據生產線平衡公式得出，T=25s/件；線平衡率P=58.11%；線平滑指數SI=1.52；根據以上數據裝配線的初始平衡在一個基本滿意狀態。

1.2 數學建模

設定相關參數符號如下：

N：裝配任務總數；

i：產品作業任務編號，I 總的產品裝配作業任務數（i=1，2，…，I）；

Q：產品品種編號（Q=1，2，3）；

Wq：第q 種產品的需求比例；

K：工作站數；

CT0：裝配線理論生產節拍；

Ak：第k 個工作站被占用時為1，未占用時為0；

Tiq：作業任務第q 種產品作業時間；

F：工作站中各工序為串聯時為1，并聯時則為0；

設定決策變量如下：

Xik作業任務分配到第個工作站時為1，否則為0。

模型假設：

①每個作業任務的加工緊前緊后關系已知；

②每個作業任務的加工標準工時已知；

③不同品種的相同裝配任務均安排在同一個工作站；

④確定每個作業任務的裝配時間，裝配線上不同產品具有相同作業任務，但是裝配時間可能不同；

⑤原有的舊裝配線基本平衡，且各作業人員能勝任所分配的裝配任務；

⑥混流裝配線上裝配的產品類型不同，但是裝配的產品具有相同的工藝和結構。

式（1）是保證N 項裝配任務都只被分配到其中的一個工作站k。

式（2）是表示作業任務必須滿足裝配任務順序約束；

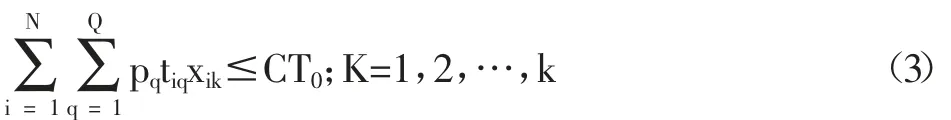
式（3）是表示K 個工作站的作業總時間均不能超過擬定的生產節拍CT0；

式（4）是表示在新的平衡中，i 裝配任務被分配到工作站K 的決策變量是0/1 型。

設置綜合評價函數：

在分析混流裝配線中出現的實際問題后，建立出工作地的工作負荷均衡和工作地實際生產節拍最小化兩個優化目標的數學模型。

①目標函數一：在滿足理論生產節拍的基礎上，且工作地數已知的情況下，要使實際生產節拍足夠小。其數學模型如（5）所示。

②目標函數二：采用各工作地負荷均衡指數SI 來進行判斷，即取每個工作地裝配時間加權值的方差。在滿足生產節拍的同時，各工作地負荷均衡指數SI 要盡量小。其數學模型如（6）所示。

綜合評價函數：運用加權法對多目標優化問題中的多個目標按其重要程度賦以適當的權重系數，把復雜的多目標優化問題轉變為單目標問題進行求解，這樣不僅能夠降低求解的難度還能保證生成解的質量。式（7）式表示最小綜合評價值Z，其中a，b 為權重系數，滿足a+b=1。

計算目標權重：

①優化目標重要程度的判斷矩陣構建：

生產節拍最小化能夠提高裝配線的裝配效率，它是保證產品能夠按時交付的關鍵目標。因此，生產節拍比工作站平滑指數重要。根據這兩個目標之間的重要程度可以構造出多目標的判斷矩陣如表2 所示。

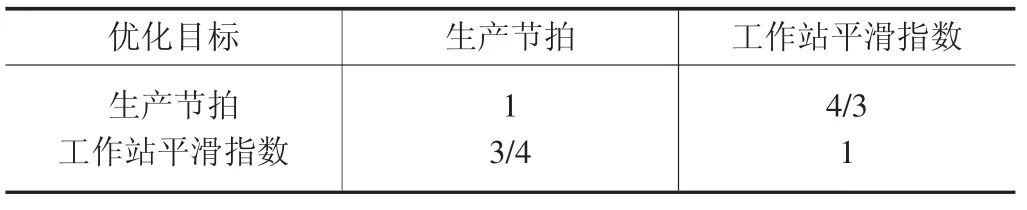
表2 多目標判斷矩陣

②目標權重的計算：依據上述多目標的判斷矩陣，可以計算得出兩個優化目標的權重。運用MATLAB 的eig 函數計算判斷矩陣的最大特征值和最大特征向量。

A=[1 4/3；3/4 1]；

[x，y]=eig（A）；%求得x 為特征向量矩陣，y 為特征值矩陣。

[mm]=find（y=max（max（y）））；%找到y 中對應最大的特征值所在列m。

w=x（:，m）/sum（x（:，m））%w 即為矩陣A 的權重。

計算結果：最大特征值為2，特征向量的分量值對應著每個優化目標的權重。w=[0.5714；0.4286]。

③一致性檢驗：判斷矩陣由分析者憑個人知識及經驗建立起來的，難免存在一些誤差。為使判斷結果與實際相吻合，需要對判斷矩陣進行一致性的檢驗。但由于二階矩陣完全一致故不需要一致性檢驗。

因此生產節拍、工作站平滑指數優化目標權重為：

a=0.5714，b=0.4286

1.3 算法設計

雙種群遺傳算法的特點是具有兩個子種群。并且這兩個子種群分別單獨進化，他們只是在保留各種群最優染色體后，依著規定的規則相互之間進行交流。這種方式的優勢在于：每個子種群的即可以單獨進化去確保其各自種群的特性，而在子種群間互相交流則確保了可行解快速的收斂的同時，也擴大了搜索范圍，增強了種群的多樣性，也避免了陷入局部最優的困境。

雙種群遺傳算法流程如圖2 所示，改進遺傳算法解決混流生產線平衡問題時，設置以下參數：

圖2 算法流程圖

①種群數量N。參考文獻[3]推薦的初始種群規模在20-160 之間。

②交叉概率C。即種群中染色體進行交叉的概率。

③變異概率M。即種群中染色體發生變異概率。文獻[3]推薦的經驗值為0.005-0.2。

④遺傳代數G。

⑤綜合評價函數Z。為式（7）中的值，目標函數值越小越符合條件。

⑥選擇策略S。為了避免在遺傳中對最優解的破壞，選擇保優策略。選擇策略為在每代遺傳中保留10%的最優父代替換新一代中相應個數的最差染色體組成新種群。這樣既保留了父代最優解，同時也保證了能夠產生足夠多的子代進行交叉、變異，最大程度的保證了新一代染色體的優秀度。

⑦交換和保留策略E。找到種群1 中經過交叉、變異之后的最優染色體，并標記位置和存儲綜合評價指標Z；找到種群2 中進過交叉、變異之后的最優染色體，并標記位置和存儲綜合評價指標Z。將種群1 的最優染色體和種群2 的最優染色體進行交換。比較兩種群最優染色體的Z值。將最小Z 值的染色體視作最好的染色體并保留下來。

1.4 算例分析

企業調整生產計劃，改進現有的產品裝配工藝，將原來的裝配作業元素除塵優化，新加入裝配作業元素自動除塵、復判，且手機殼三種型號的日均產量調整為A:B:C=500:1500:1000，三種產品總需求量為3000 片。改變后該生產線總共有21 個工序，16 個工作站。表3 為三種產品經過21 道工序所對應的加工時間。表4 為兩個種群具體算法參數設置。

表3 各工序加工時間

表4 各種群算法參數

1.5 優化結果

適應度進化曲線如圖3 所示。從曲線的走勢來看收斂性良好，在運行到第26 代即找到了近似最優解。

圖3 適應度進化曲線

最優排布如圖4 所示。圖中字段列表示工作站的編號。gs 列中數字表示該工作站包含幾個工序。Ct 列代表計算出的該工作站的生產節拍。Job 代表生成的工作站里包含的工序，其中數字代表在表3 中工序的順序。flag 代表該工作站的串并聯關系。為0 時代表為并聯，為1 時代表為串聯。

圖4 最優染色體

2 方案評價

各工作站作業時間如圖5 所示。結果表明裝配線平衡率提升了8.43%，各工作站生產負荷減少了0.9305。

圖5 工作站作業時間

經過混流裝配線平衡后的各工作站生產節拍比平衡前更加均衡，尤其對于每一個工作站的生產負荷來看分配更均衡。這樣提高生產線的整體運行效率，在一定程度上降低了生產線運作成本，提高了J 公司的運作管理水平。

3 小結

以成都有限公司為案例，均衡分配工作站裝配任務，重新規劃布局。提高企業混流裝配線生產的柔性、提高企業生產效率、縮短轉產時間、降低企業生產成本，使企業在現今市場更具有競爭力。

然而，本文是以最小工作節拍和最小工作負荷為優化目標，針對不同優化目標的組合的生產線平衡問題還有待于進一步研究。本文沒有考慮串并聯生產系統對人的影響，針對串并聯生產系統對人因的影響還有待于進一步研究。