地鐵鋼彈簧浮置板阻尼參數試驗及其對行車的影響研究

程曜彥,方宏凱,李新國

(同濟大學教育部道路與交通工程重點試驗室,上海 201804)

鋼彈簧浮置板軌道自1977年由Grootenhuis[1]首先提出并成功應用于德國科隆地鐵，作為目前在城市軌道交通減振降噪研究領域應用最為廣泛、效果最受認可的減振結構，一直是該領域研究的熱點。鋼彈簧浮置板減振軌道結構由一定質量、剛度的混凝土道床板和鋼彈簧組成的質量-彈簧減振系統，相比于其他軌道減振型式具有固有頻率低、減振效果良好的特點，試驗和研究表明其減振效果可達20～30 dB[2]。

在鋼彈簧浮置板的減振性能研究方面，國內外學者相關研究成果如下：Cui等[3]采用無限長Timoshenko梁模擬鋼軌，結果表明浮置板軌道對頻率高于 15 Hz的振動衰減作用明顯；吳天行[4]、李增光等[5]和王炯等[6]在頻域內建立了車輛-軌道結構系統的數值計算模型，對比了浮置板軌道的減振、隔振性能；吳磊[7]在提出地鐵車輛-鋼彈簧浮置板軌道動力學耦合模型及其數值計算程序的基礎上，較為全面地研究了鋼彈簧浮置板減振降噪性能。

鋼彈簧浮置板道床對于小于20 Hz的低頻段尤其是結構固有頻率附近頻段，其減振效果較差甚至產生振動放大效應，這些低頻振動對于一些高精密儀器和生產設備的正常工作具有很大的影響。研究發現，在剛度不發生改變的情況下，適當增加阻尼耗能可以有效地減小結構低頻段的振動[8-10]。鋼彈簧隔振器的阻尼是影響浮置板軌道減振效果的關鍵參數，因此，選擇合適的測試方法及傳感器參量來準確測試鋼彈簧阻尼隔振器組件阻尼，是明確浮置板軌道減振效果的前提，也可用來驗證產品是否滿足設計要求[11-14]。在軌道結構減振系統中添加阻尼，可以抑制系統振幅，使列車通過浮置板時較為平順，但阻尼過高會降低系統的減振效率，同時，阻尼比的測試也是軌道動態性能測試的一個必測項目[15-19]。因此，阻尼相關參數的選擇對于列車平穩運行及環境振動有著重要影響。

綜上所述，鋼彈簧浮置板軌道結構的阻尼設置在振動傳遞中作用關鍵。盡管針對這方面的研究已經成為近年來最熱門的問題之一，但是目前對于鋼彈簧浮置板隔振器的阻尼取值方面的研究仍然不夠成熟。結合鋼彈簧隔振器阻尼錘擊試驗及車輛-軌道-橋梁系統耦合數值分析兩種方法，分析了鋼彈簧隔振器阻尼參數設置對鋼彈簧浮置板軌道系統動力響應及地鐵車輛行車平穩性、安全性的影響。

1 鋼彈簧隔振器阻尼比測試

1.1 測試原理

鋼彈簧浮置板減振軌道結構是將一定質量和剛度的混凝土道床板浮置于由鋼彈簧和鋼套筒組成的隔振器上構成質量-彈簧-隔振系統，其主要由基底、浮置板、隔振器、軌枕、扣件以及鋼軌等組成，可有效隔振、減振。如圖1所示。

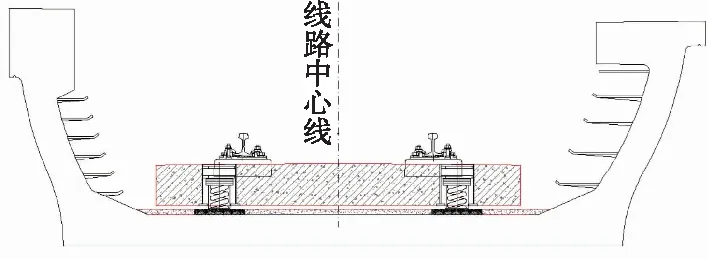
圖1 鋼彈簧浮置板結構橫斷面

隔振效果通常用隔振系數η和隔振效率E來衡量，計算方法如式(1)所示。

(1)

式中，ξ為阻尼比；λ為激振頻率與固有頻率之比。

鋼彈簧隔振器阻尼比的測試原理為將一鋼彈簧隔振器放置于水平地面上，在隔振器正上方居中放置質量為m的混凝土質量塊，組成等效的單自由度質量-彈簧-阻尼系統。如圖2所示。

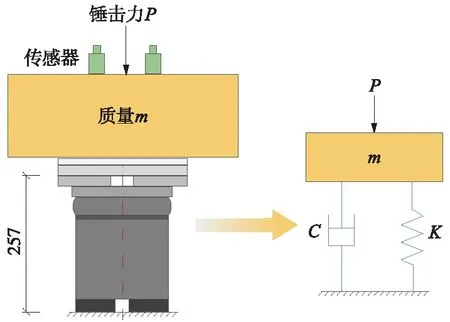
圖2 鋼彈簧隔振器阻尼比測試原理(單位：mm)

該系統的自由振動方程，如式(2)所示。

(2)

式中：m為質量塊的質量；c為阻尼器的阻尼系數；k為鋼彈簧剛度。

考慮到測試系統為小阻尼體系，令u(t)=est，并將其代入式(1)，得到式(3)～式(6)。

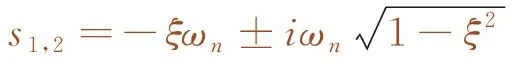
(3)

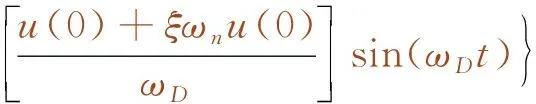
(4)

c=2mωnξ

(5)

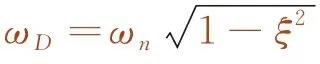
(6)

則任意兩個相鄰振動峰值之比，如式(7)所示。

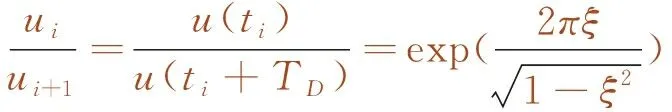
(7)

由式(7)可知，鋼彈簧隔振器相鄰振動峰值之比僅與阻尼比有關，與i無關。

式中，λ為對數衰減率，表示相鄰振動峰值比的自然對數值；由于該系統為小阻尼體系，為獲得更高精度的測試結果，可采用相隔n個周期的振動峰值比來計算其阻尼比。

相隔n個周期對數衰減率λ和阻尼比ξ，如式(8)所示。

(8)

其中，λ為單個波形的對數衰減率；n為自由振動波形個數；ui為第i個波峰幅值；ui+n為第i+n個波峰幅值。

1.2 測試方案

鋼彈簧隔振器阻尼比測試系統主要由1.2 t混凝土質量塊、891-2型拾振器(傳感器)、891型六線放大器及DH5920動態信號測試分析系統組成。如圖3所示。

圖3 鋼彈簧隔振器阻尼比測試系統

根據鋼彈簧隔振器實際受力時的狀態，測試選取質量為1.2 t的混凝土質量塊，置于隔振器正上方；質量塊離開地面一定高度，以保證在錘擊的過程中質量塊不會因接觸地面而影響測試結果；質量塊上表面中心處放置一塊鐵墊板，即錘擊力的施加位置；為保證測試精度，在靠近質量塊中心位置對稱放置4個相同的傳感器，數據處理時取4個傳感器的測試數據的平均值作為測試結果。

在錘擊力施加位置對混凝土質量塊m分別施加4檔不同大小的錘擊力，當被測試系統激振時，在傳感器上獲取加速度、速度、位移對應測試數據，同時統計出4檔錘擊力錘擊時傳感器得到的測試數據分別對應的加速度、速度、位移指標大小范圍，作為區分4檔錘擊力大小的控制范圍，如表1所示。為消除測試時隨機誤差，先設置1組平行試驗。

表1 4檔錘擊力條件下傳感器產生的測試指標范圍

1.3 測試數據的處理與分析

為提高測試數據精度，須消除由于質量塊在各種模態振動、環境振動等產生干擾的信號，因此，將4個傳感器通道得到的原始數據導入MATLAB，并通過巴特沃斯濾波方法，濾除試驗系統固有頻率±20%范圍以外的頻率，以得到較平順的波形。固有頻率計算公式為

(9)

已知測試系統的靜剛度k=5.606 N/mm；試件的質量m=1.2 t；計算ωn=10.88 Hz，濾波之后留下的是頻率在8.704～13.056 Hz之間的曲線部分。

經由Matlab軟件編制的濾波函數程序處理后，得到可進行計算的數據圖像并舍棄第一個峰值，從第二個峰值開始計算，并代入到理論計算部分中的阻尼比計算公式(8)中，即可得到阻尼比實測值。按照測試方案中施加4檔錘擊力錘擊質量塊產生垂向振動時測得加速度、速度、位移的各10組有效數據。選擇自由衰減振動波形中的峰值間隔周期n=1～5進行計算，得到阻尼比數據經MATLAB程序處理結果。如表2所示。

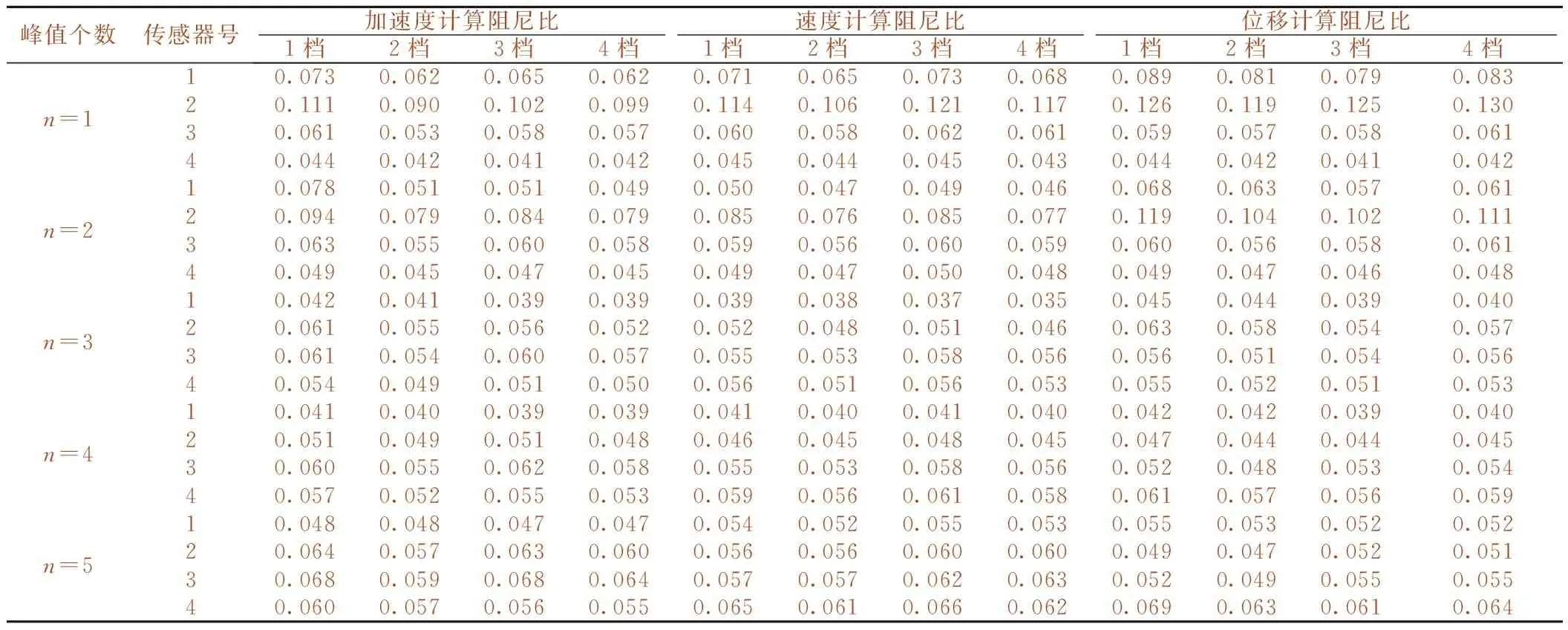
表2 4檔錘擊力加載測得的阻尼比平均值計算結果

(1)通過選取傳感器的測試參量為加速度、速度、位移時測試得到的阻尼比平均值對比，可知1檔時的誤差百分比分別為9.138%，2.131%和5.30%，誤差較大，略去；2檔～4檔時的誤差百分比分別為1.0%～2.8%，1.1%～3.9%，1.5%～2.3%。因此，錘擊力在2檔～4檔內，錘擊力大小對測試結果的影響較小。

(2)通過對比傳感器測試參量分別為加速度、速度、位移時測試得到的阻尼比平均值得到的誤差百分比，n=1，n=2和n=5時的誤差百分比分別為13%～22%、8%～18%、2%～8%，誤差較大，略去。自由衰減振動波形中峰值間隔周期n=3，n=4時，在選擇加速度、速度、位移為測試參量時測得阻尼比最大誤差分別為0.2%，1.6%，2.4%，誤差較小、參數選擇合適。

(3)分別采用自由衰減振動波形中峰值間隔周期n=1～5，來計算選用測試參量為加速度、速度、位移的傳感器測試得到的阻尼比與n的關系如圖4所示。

圖4 測試參數為傳感器測試得到的阻尼比與n的關系

由傳感器的加速度、速度、位移參量測試得到的阻尼比與選擇不同n時計算得到對應阻尼比均值的誤差百分比如圖5所示。

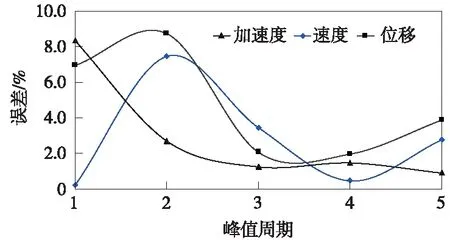
圖5 加速度、速度、位移傳感器測試得到的阻尼比與選擇不同n時計算時得到對應的阻尼比均值的誤差百分比

由圖4與圖5可知，采用加速度、速度、位移傳感器上得到的阻尼比三者之間的關聯性隨著n值的增加較好，尤其是在n=3、n=4時，3種參數的傳感器阻尼比最大相差0.003，阻尼比最大誤差百分比在3%以下。

2 鋼彈簧阻尼對橋上浮置板軌道結構振動傳遞特性分析

2.1 鋼彈簧浮置板-箱梁橋結構模型

橋上浮置板軌道結構模型中鋼軌采用CHN60鋼軌，彈性模量2.1×1011N/m2，密度7.85×103kg/m3，泊松比0.3，鋼軌橫截面積7.7×10-3m2；扣件剛度1.0×107N/m，阻尼5.0×104N·s/m，扣件間距0.6 m；浮置板密度為3 000 kg/m3，彈性模量為3.45×1010N/m2，泊松比為0.17，尺寸為31.8 m×3.4 m×0.3 m；鋼彈簧剛度為6×106N/m，阻尼為1×104N·s/m，鋼彈簧間距為1.5 m；橋梁結構為單跨32 m箱梁，梁體密度為3 000 kg/m3，彈性模量為3.35×1010N/m2，泊松比為0.167；橋墩剛度為3×109N/m，阻尼為1×105N·s/m。如圖6所示。

圖6 鋼彈簧浮置板-箱梁橋結構模型

數值計算軟件采用ANSYS軟件，其中采用歐拉梁模擬鋼軌單元，彈簧單元模擬扣件，實體單元模擬浮置板，鋼彈簧采用彈簧單元模擬，實體單元模擬橋梁。

2.2 鋼彈簧阻尼對橋上浮置板軌道結構振動傳遞特性分析

鋼軌、浮置板以及橋梁的位移導納和橋墩傳遞的力導納可作為輪軌作用力向下的傳遞特征[19-22]分析鋼彈簧阻尼浮置板軌道結構振動傳遞特性。本節計算了浮置板軌道結構的鋼彈簧阻尼分別為10，30，50 kN·s/m條件下1～500 Hz頻段內車輛動荷載作用點正下方的鋼軌位移、浮置板位移、橋梁位移以及橋墩傳遞下的作用力變化情況，不同阻尼作用下的軌道結構的動力響應。如圖7所示。

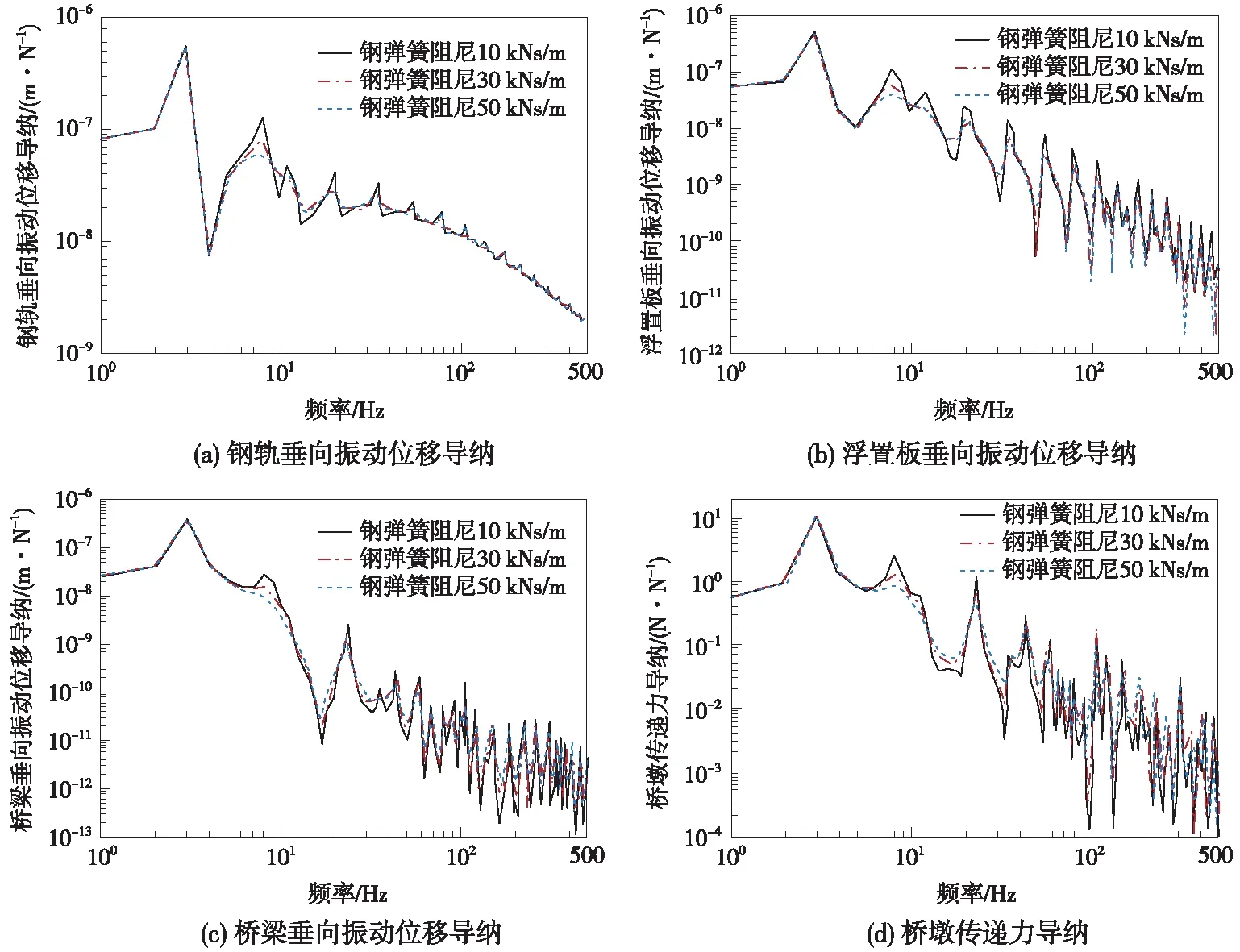
圖7 3種鋼彈簧阻尼作用下軌道結構振動傳遞特性

簡諧激勵為3 Hz時對應的由橋梁共振引起響應幅值及軌道結構的第一共振頻率(8 Hz)對應的響應幅值如表3所示。

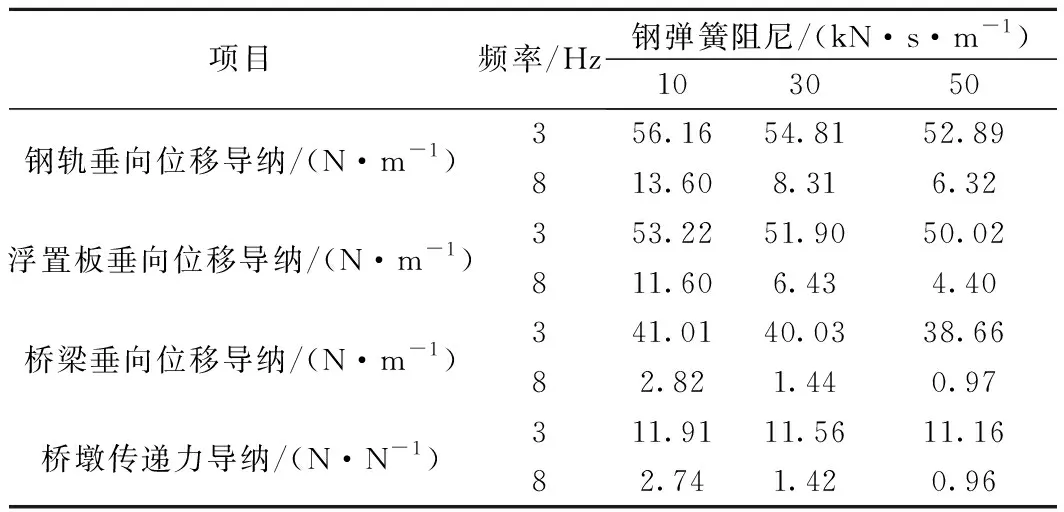
表3 3種鋼彈簧阻尼作用下的振動傳遞特征幅值

如圖7、表3所示，在簡諧激振1～500 Hz時，在鋼彈簧阻尼分別為10，30，50 kN·s/m時，浮置板垂向位移導納在第一共振峰處的幅值分別為11.60×10-8，6.43×10-8m和4.40×10-8m，表明軌道結構在第一共振峰處的振動響應隨著鋼彈簧阻尼的增大顯著減小。

3 鋼彈簧阻尼參數對行車影響分析

3.1 車輛-軌道-橋梁動力耦合模型

車輛-軌道-橋梁動力相互作用系統主要由車輛、軌道、橋梁3個子系統構成，子系統之間通過輪-軌關系、橋-軌關系進行系統耦合，是典型的復雜空間耦合時變系統，如圖8所示。為建立車輛-軌道-橋梁系統仿真模型，在分析了浮置板軌道-簡支箱梁橋振動特性基礎上，利用SIMPACK與ANSYS聯合仿真。

圖8 車輛-軌道-橋梁耦合模型

地鐵車輛多體動力學模型在SIMPACK中搭建，車輛類型為B型；軌道和橋梁子結構分析在ANSYS中完成。假設軌-梁-墩為柔性系統，生成所需要的*.cdb和*.sub文件，再將作為柔性體的結構模型導入SIMPACK，各部件通過非線性彈簧阻尼力元連接。由于多體動力學軟件中幾何外形不參與動力學計算，可在SIMPACK中直接調用默認車體幾何外形。鋼軌建模參考CN-60型參數，且只考慮橋梁段上的軌道為柔性體結構。之后通過*.fbi文件及編寫包含軌道信息的*.ftr文件來搭建柔性軌道，并實現輪軌間數據交互。

計算條件：車速為60 km/h及80 km/h；浮置板鋼彈簧阻尼為10～70 kN·s/m；計算時列車單線靠左側勻速通過橋梁區段。

3.2 鋼彈簧阻尼對地鐵車輛動力響應影響分析

不同鋼彈簧阻尼及行車速度條件下對地鐵車輛動力響應的影響，如圖9所示。

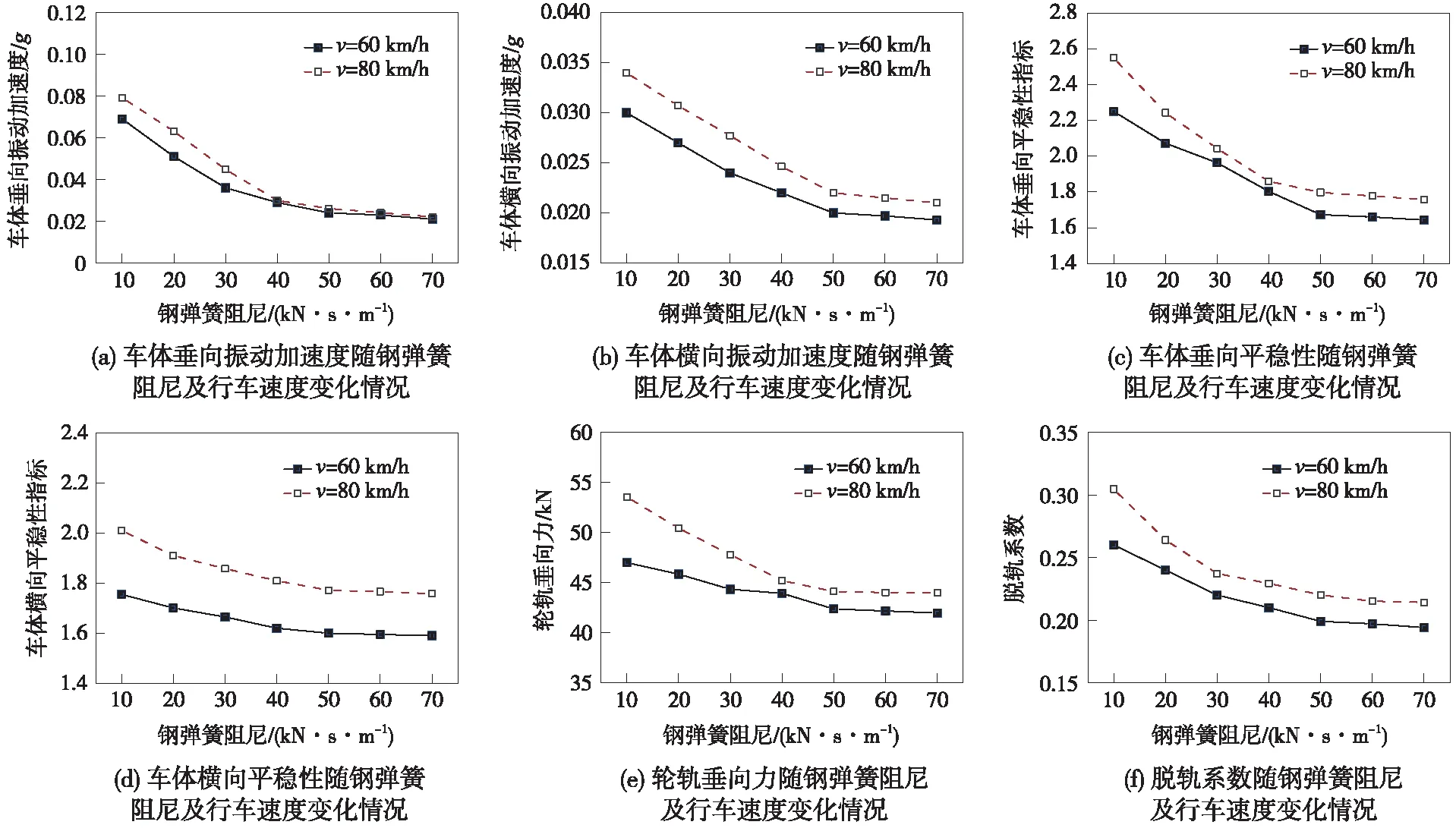
圖9 鋼彈簧阻尼及行車速度對車輛動力響應的影響

在車輛速度分別為60 km/h和80 km/h條件下，改變鋼彈簧阻尼對車輛行車平穩性及安全性評價指標的影響規律大體一致，各指標值均隨阻尼的增大而減小、隨行車速度的提高而增大。

(1)依據車輛平穩性指標隨鋼彈簧阻尼及行車速度變化情況，在行車速度一定的情況下，各指標值均隨著鋼彈簧阻尼增加而減小：在行車速度為60 km/h時，車體橫向加速度和垂向加速度分別由0.031g減小為0.029g、0.069g減小為0.021g，橫向平穩性和垂向平穩性則分別由1.755減小為1.591，由2.255減小為1.643。由此說明，增加鋼彈簧阻尼可提高旅客乘坐舒適度，但是當鋼彈簧阻尼大于50 kN·s/m時，各平穩性指標的變化幅度相差很小。這是由于鋼彈簧阻尼是由具有強烈非線性阻尼特性(遲滯特性)的橡膠、聚合體等彈性元件提供，橡膠的阻尼隨著阻尼的增加，只對高頻振動的傳遞率稍有影響。車輛平穩性指標計算時，對于車輛地板振動加速度大于20 Hz時計權系數取為1，說明大于20 Hz的振動對于車輛平穩性影響較小。因此，當鋼彈簧阻尼高于某個值(50 kN·s/m)時，平穩性指標變化較小。

(2)依據車輛安全性指標隨鋼彈簧阻尼及行車速度變化情況，在行車速度一定的情況下，車輛安全性指標均隨著鋼彈簧阻尼增加而減小：以相對不利的行車速度即80 km/h為例，增大鋼彈簧阻尼，輪軌垂向力逐漸減小，最大為53.2 kN，遠小于170 kN的安全限值，在鋼彈簧阻尼大于50 kN·s/m后輪軌垂向力基本保持不變；車輛脫軌系數隨著鋼彈簧阻尼的增加而減小，在鋼彈簧阻尼大于50 kN·s/m時，脫軌系數在0.2附近變化不大，表明此時鋼彈簧阻尼的變化對車輛脫軌系數的影響已不明顯。這是由于輪軌相互力包含高頻P1力和準靜態P2力，用于脫軌系數計算時的車輪施以鋼軌的橫向作用力Q和車輪作用于鋼軌的垂向作用力P為準靜態力，而鋼彈簧阻尼隔振器的阻尼增加時，由于橡膠阻尼特性只對高頻振動傳遞率稍有影響，當鋼彈簧阻尼大于某個值(50 kN·s/m)時，阻尼對車輛脫軌系統影響不明顯。

4 結論

結合鋼彈簧隔振器阻尼錘擊試驗及車輛-軌道-橋梁耦合數值計算兩種方法，分析了鋼彈簧隔振器阻尼參數對鋼彈簧浮置板軌道系統動力響應及行車平穩性的影響，得到了鋼彈簧浮置板軌道振動傳遞特性及阻尼參數對地鐵車輛行車的影響，結論如下。

(1)根據鋼彈簧隔振器阻尼比測試室內試驗數據，可選取測得加速度、速度、位移數據來計算鋼彈簧隔振器阻尼比；鋼彈簧隔振器阻尼參數試驗表明，錘擊力在2檔至4檔是錘擊力選擇的合適范圍；當n取值為3和4時阻尼比計算結果相差不大，在計算自由衰減振動的鋼彈簧阻尼比時，波形峰值間隔周期n值合適的選擇為3和4；在錘擊法測試鋼彈簧隔振器阻尼比試驗中，選用加速度、速度、位移作為測試參量，計算得到的鋼彈簧隔振器阻尼比結果最大誤差在3%以內，表明選取傳感器3種測試參量阻尼比測試結果基本一致，均可作為測試指標值。

(2)鋼彈簧阻尼變化對軌道結構振動傳遞特性的影響分析表明，在簡諧激振 1～500 Hz內時，軌道結構在第一共振峰處的振動響應隨著鋼彈簧阻尼的增大而顯著減小：在鋼彈簧阻尼分別為10，30，50 kN·s/m時，浮置板垂向位移導納在第一共振峰處的幅值分別為11.05×10-8，6.12×10-8，4.19×10-8m·N-1。

(3)通過對鋼彈簧阻尼參數對行車安全及車輛穩定性影響分析表明，增加鋼彈簧阻尼，列車運行的安全性及舒適度均會提高，但在阻尼系數大于50 kN·s/m時對于行車安全及車輛穩定性的影響不明顯，因此，設計時在保證隔振效果的前提下，綜合考慮建議阻尼設置不宜超過50 kN·s/m。