基于表面V形溝槽的圓柱減阻性能研究

江興隆，歐陽凌浩，李 超

（中國船舶集團有限公司第七一〇研究所，湖北 宜昌 443003）

0 引言

水下拖曳系統是進行海洋探測的重要手段，廣泛應用于海洋環境監測、資源勘探、軍事等眾多領域。進行大深度拖曳時，水下拖曳系統的阻力主要由拖纜產生[1]。拖纜的阻力過大，導致定深變差，影響拖曳系統的工作性能。拖纜在水中的運動，可看為多段不同迎流角圓柱的運動，所以拖纜的減阻可看作多段圓柱的減阻，本文采用表面溝槽的減阻方式來減小圓柱阻力。

Walsh等人[2]最先開展溝槽減阻性能的研究，并發現對稱的 V型條紋溝槽表面在湍流條件下可減阻8%。Bechert和Brused[3]測試了多種形狀的溝槽條紋，V型溝槽減阻效果可達10%。Lim[4]通過在圓柱體上橫向布置O形圈，對圓柱繞流進行控制，最大有9%的減阻效果。Quintavalla S J[5]發現低深徑比溝槽可以顯著降低繞流阻力，且所有溝槽占總圓柱截面積比值會影響臨界雷諾數。Huang S[6]在拖曳水池測量了矩形溝槽圓柱的繞流升阻力。王灃浩[7]設計了一種波狀圓柱，其脈動升阻力系數減小，并通過實驗得到最大減阻效果為20%。廖崇吉[8]進行了溝槽圓柱體的數值仿真計算，在雷諾數Re=40 000時，最大減阻率為16.3%。錢權[9]開展了V型溝槽圓柱繞流數值模擬研究，最大減阻率可達28.4%。齊野含[10]發現溝槽圓柱能夠抑制表面旋渦的影響區域范圍，提高旋渦的流向尺度，并通過水槽試驗驗證了仿真結果。

目前，國內外關于溝槽減阻研究已經有很多，但很少對有一定傾斜角的溝槽圓柱進行研究，表面溝槽對拖纜的減阻也還未形成系統的研究。本文對V形溝槽圓柱的減阻研究，討論了溝槽參數、雷諾數及迎流角對減阻性能的影響，對今后溝槽纜的實際設計使用具有一定的參考價值。

1 V形溝槽圓柱模型

1.1 幾何模型

圓柱直徑D=20 mm，V形溝槽沿圓柱的周向均勻分布。溝槽的尺寸主要由3個參數確定，分別為溝槽深度h、溝槽寬度s、溝槽數量n，得到如圖1所示的模型示意圖。

圖1 溝槽圓柱模型圖Fig.1 Model diagram of groove cylinder

1.2 溝槽深度尺寸確定

Walsh等人[1]對溝槽平板的減阻性能研究可知：無量綱溝槽深度h+≤25時，溝槽具有很好的減阻效果，本文借鑒該研究成果進行溝槽圓柱的參數設計。

無量綱溝槽深度：

壁面剪切速度：

壁面剪切應力：

邊界層厚度：

由式（3）和（4）代入式（2），得：

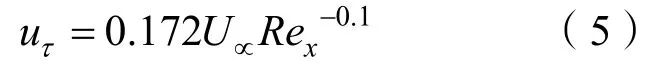
從而得到無量綱溝槽深度為

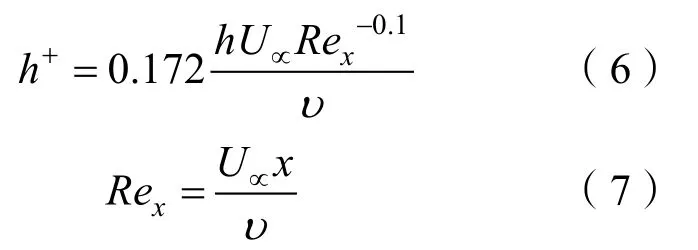
式中：h為溝槽深度；U∝為來流速度；υ為運動粘性系數。

來流速度為2 m/s、h+取為25時，通過式（6）計算得到溝槽深度h=0.21 mm，即h≈0.01D，后續進行數值模擬時，溝槽深度在0.01D附近選取。

2 網格無關性分析

獲得適合溝槽圓柱的仿真模型，確定影響仿真模擬的重要參數，使計算結果準確。在雷諾數Re=40 000、圓柱直徑D=20 mm時，采用光滑圓柱進行仿真計算。

在保證流場不受邊界尺寸影響的前提下，選擇計算域20D×10D，前后邊界面距離圓心5D，上游邊界面距離圓心 5D，下游邊界面距離圓心 15D，如圖2所示。

圖2 計算域Fig.2 Computing domain

采用多面體網格進行全局的網格劃分，該網格可很好地在小尺寸溝槽圓柱表面劃分規則網格。在仿真計算中，采用SSTk-ω湍流模型，該模型算法穩定性好，可很好地模擬精細化局部流場，對物體近壁區的流場有很好的計算精度。該模型要求圓柱壁面到最近的網格節點高度的無量綱數y+≈1，當來流速度為2 m/s時，計算得出第1層邊界層的高度為0.008 5 mm。

圖3 計算域局部網格劃分Fig.3 Computing domain local meshing

分別選取3種網格基準值0.018 m、0.015 m、0.012 m，測得平均阻力值如表1所示。

表1 不同網格尺寸比較表Table 1 Comparison table under different mesh sizes

從表中可看出，網格基準值為0.015 m、網格數目為147萬時，阻力系數為1.19，與Norberg C的試驗結果誤差最小，網格基準值選為0.015 m。

3 數值模擬結果分析

第2章節得到了仿真模型的重要參數，即圓柱展長為D，網格基準值為0.015 m，用于V形溝槽圓柱的數值模擬。

3.1 雷諾數Re

迎流角θ=90°，雷諾數Re分別為 20 000、30 000、40 000、50 000時，模擬光滑圓柱和V型溝槽圓柱的平均阻力系數，得到如圖4所示的變化曲線。

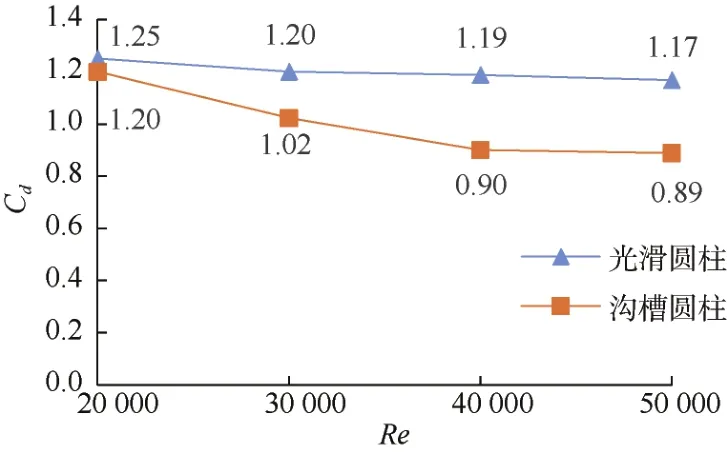
圖4 不同雷諾數下升阻力系數的變化曲線Fig.4 Variation curves of drag coefficient under different Reynolds numbers

圖4中，隨雷諾數的增加，光滑圓柱的阻力系數變化不明顯，阻力系數約為1.2。V型溝槽圓柱的升阻力系數隨雷諾數的增加而呈現減小趨勢，當雷諾數Re>40 000后，升阻力系數的變化較緩，具有很好的減阻效果。

3.2 溝槽參數

在雷諾數Re=40 000、迎流角θ=90°時，分別研究溝槽深度h、溝槽寬度s、和溝槽數量n對減阻效果的影響。

3.2.1 溝槽深度

分別仿真計算溝槽深度h為0.005D、0.007 5D、0.01D、0.012 5D、0.015D時，穩定時間段內V型溝槽圓柱的平均阻力系數，如圖5所示。

圖5 不同溝槽深度下阻力系數變化曲線Fig.5 Variation curves of drag coefficient under different groove depths

由圖5看出，5種溝槽深度下的阻力系數均小于光滑圓柱，說明選取的溝槽深度都具有一定的減阻效果。當溝槽深度大于0.007 5D時，隨h的增加，阻力系數變大；當溝槽深度小于0.007 5D時，隨h的增加，阻力系數變小。可知，當h=0.007 5D時，溝槽圓柱具有最佳的減阻效果。

3.2.2 溝槽寬度

溝槽寬度s分別為0.055D、0.06D、0.065D、0.07D、0.075D時，計算穩定時間段內V型溝槽圓柱的平均阻力系數，如圖6所示。

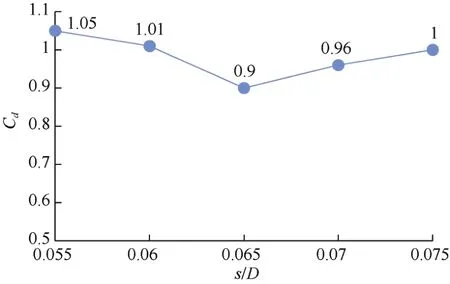
圖6 不同溝槽寬度下阻力系數變化曲線Fig.6 Variation curves of drag coefficient under different groove widths

如圖6所示，5種溝槽寬度的阻力系數均小于1.19，具有一定的減阻效果。當溝槽寬度s大于0.065D時，隨s的增大，阻力系數變大，從圖中趨勢可判斷，s增大到一定值后，可能會起到增阻效果；溝槽寬度s小于0.065D時，隨s的減小，阻力系數變大，光滑圓柱即s=0，不再具有減阻效果。當s=0.065D時，阻力系數最小，減阻效果最佳。

3.2.3 溝槽數量

溝槽數量n分別為24、30、36、40時，計算穩定時間段內 V型溝槽圓柱的平均阻力系數，如圖7所示。

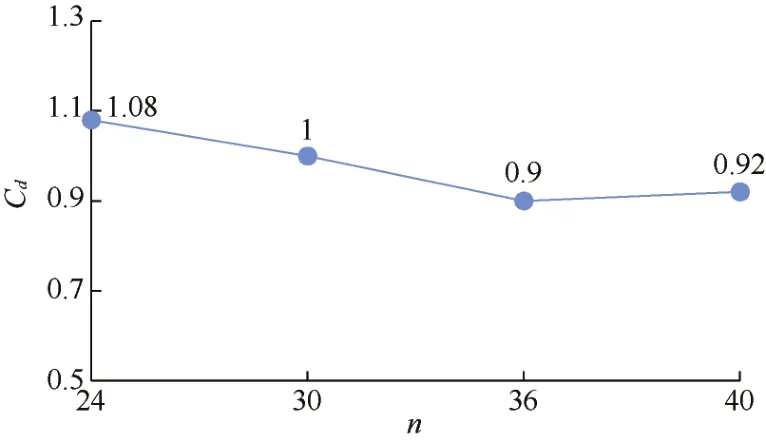
圖7 不同溝槽數量下阻力系數變化曲線Fig.7 Variation curves of drag coefficient under different groove numbers

圖7中，溝槽數量n小于36時，隨著數量n的減小，阻力系數變大；溝槽數量n大于36時，阻力系數略微增加。當n=36時，阻力系數最小，減阻效果最佳。

3.3 迎流角

在迎流角θ分別為 90°、75°、60°、45°和 30°條件下，數值模擬計算光滑圓柱和 V型溝槽圓柱的時均阻力系數，得到5種迎流角下的阻力系數Cd和減阻率η的變化曲線，如圖8所示。

圖8 不同迎流角下減阻性能變化曲線Fig.8 Variation curves of drag reduction performance at different attack angles

圖8中，2種圓柱的阻力系數Cd隨迎流角θ的增加而增大。迎流角θ大于 45°時，光滑圓柱的阻力系數大于溝槽圓柱，溝槽結果產生減阻效果；迎流角θ小于 45°時，光滑圓柱的阻力系數小于溝槽圓柱，溝槽結構增阻，隨θ的減小，增阻效果越明顯。θ=90°時，減阻效果最好，減阻率達24%。

4 水槽試驗結果分析

4.1 試驗件

本次試驗在哈爾濱工程大學的水槽實驗室進行。由于試驗的測力天平的測量量程影響，為盡量減小測量誤差，試驗件的長度取為200 mm。如圖9所示，溝槽數量分別為36個、30個、24個的V形溝槽圓柱，長度為100 mm、200 mm的光滑圓柱，圓柱前端為M8的螺紋，后端為M8的螺紋孔。長度100 mm的光滑圓柱，與試驗件的后端部相連，用于減弱圓柱端部繞流阻力的干擾。

圖9 加工零件示意圖Fig.9 Schematic diagram of machined parts

4.2 試驗方案設計

首先，為消除水下圓柱底端繞流影響，測出1.0 m/s、1.5 m/s、2.0 m/s流速下100 mm圓柱在水下的受力情況。其次，在200 mm光滑圓柱和3種不同溝槽圓柱下端連接 100 mm圓柱，測量1.0 m/s、1.5 m/s、2.0 m/s流速下的阻力值。最后，第2次測得的阻力值減去第1次的阻力值，得到光滑圓柱和溝槽圓柱的真實阻力值。圖10為安裝示意圖。

圖10 試驗裝置的安裝圖Fig.10 Installation diagram of test equipment

4.3 試驗數據分析

試驗得到了光滑圓柱和3種溝槽數量圓柱的真實阻力，計算得到 V形溝槽圓柱的平均阻力系數Cd和減阻率η，如圖11所示。

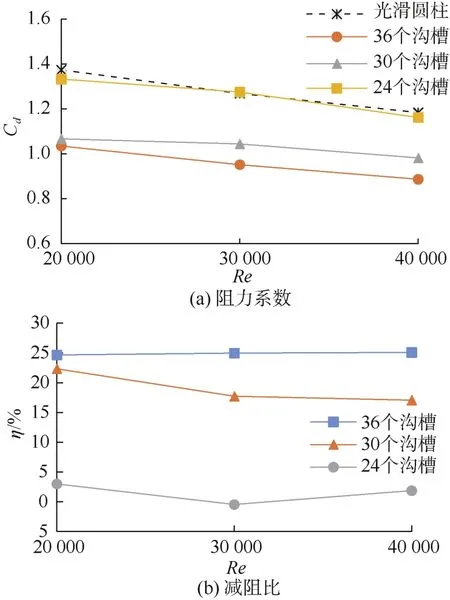
圖11 不同雷諾數下各試驗件的減阻性能變化曲線Fig.11 Variation curves of drag reduction performance of each test article under different Reynolds numbers

由圖 11可知：隨著雷諾數的增加，4種圓柱的平均阻力系數減小，且在雷諾數為40 000時，阻力系數最小。溝槽數量為36時，平均阻力系數最小，即減阻效果最好，減阻率可達25%；溝槽數量為24時，平均阻力系數與光滑圓柱相差不大，且雷諾數為30 000時，出現了增阻現象。

在雷諾數Re=40 000時，比較4種不同溝槽數量圓柱的仿真結果與試驗結果，如圖12所示。

圖12 仿真結果和試驗結果比較圖Fig.12 Comparison between simulation results and test results

從圖12可知，在雷諾數Re=40 000時，除溝槽數量為24個之外，仿真結果與試驗結果非常貼近，證明該數值模擬方法是正確的，具有很高的可信度。

5 結束語

本文研究了不同仿真模型參數對計算精度的影響，以及不同溝槽參數、雷諾數和迎流角下，V形溝槽圓柱的減阻效果，并通過試驗驗證了仿真結果。具體結論如下：

1）采用數值仿真計算的方法，對比分析升阻力系數，確定網格基準值為0.015 m。

2）對比分析了不同溝槽參數的減阻性能，得到溝槽深度h=0.007 5D、溝槽寬度s=0.065D、溝槽數量n=36時，V形溝槽圓柱具有最好的減阻效果。

3）不同雷諾數下，光滑圓柱的阻力系數在1.2附近浮動，V形溝槽圓柱的阻力系數隨雷諾數的增加而逐漸減小，最大減阻率為24%。

4）迎流角為90°時，V形溝槽圓柱的減阻效果最好，隨迎流角的減小，減阻效果變差，迎流角45°不再具有減阻效果。在溝槽纜的設計使用時，V形溝槽應布置在水下迎流角為60°～90°的位置。

5）通過比較試驗與仿真結果，發現兩者結果基本吻合，說明模擬方法正確，仿真結果具有很高的可信度。