密碼累加器研究進展及應用

苗美霞，武盼汝，王贇玲

(西安郵電大學 網絡空間安全學院，陜西 西安 710121)

密碼累加器能夠高效地證明元素是否存在于集合中。具體來講，首先將集合X={x1，…，xn}中的所有元素累加到累加器accX中，然后計算元素xi∈X的證據wi，最后利用證據wi和累加值accX來證明元素xi∈X。密碼累加器與向量承諾[1-2]、零知識集合(ZK-sets)[3-4]等原語有緊密的聯系，三者都能解決(非)成員驗證的問題。但是，三者在驗證內容、隱私性等方面存在一定的區別。向量承諾[1-2]針對有序集合(向量) 提供驗證，即不僅能夠證明元素mi存在于有序集合中，而且能證明mi是第i個位置上的消息，但是其計算復雜性較大。零知識集合[3-4]不僅能夠證明某個元素是否屬于集合，同時不泄漏任何關于集合的信息，如集合的大小。然而，零知識集合的驗證開銷與集合中元素的數量線性相關，效率較低。

BENALOH等[5]于1993年首次提出密碼累加器的概念，但是該構造為靜態累加器，即累加集合固定不變。CAMENISCH等[6]于2002年提出了動態累加器的概念，可以支持累加集合動態地添加和刪除元素。然而，上述兩類累加器僅支持集合中元素的成員證明，即xi∈X，而無法支持非成員證明，即無法提供y?X的證據。為了解決此問題，LI等[7]于2007年首次提出了通用累加器的構造，能夠同時實現成員和非成員證明。

密碼累加器自提出以來，許多學者對其進行了大量的研究并給出了具體的構造方案。基于不同的密碼工具，密碼累加器可分為基于RSA體制的累加器[5-8]、基于雙線性映射的累加器[9-12]和基于Merkle哈希樹的累加器[13]。密碼累加器有著廣泛的應用場景。在訪問控制系統中，將授權用戶的訪問權限聚合到累加器中，授權用戶通過將成員證據作為訪問憑證來訪問系統。在匿名憑證系統中[6]，需要進一步隱藏用戶的身份，將累加器和零知識證明[14]結合是解決這類問題的有效方法。在數據外包存儲中，密碼累加器可用作認證數據結構(Authenticated Data Structure，ADS)[15-18]，用戶利用計算結果和相應證據來證明計算結果的正確性。在加密貨幣中，密碼累加器通過代替Merkle哈希樹來降低通信開銷和提高驗證效率[19]。此外，累加器還可應用于時間戳[5]、隱私保護數據外包[20]、認證字典[21]、編輯[22]、負責任的證書管理[23-24]等場景中。

筆者首先從密碼累加器的構造方案和功能應用等方面對現有方案進行了分類、分析和總結；其次介紹了密碼累加器的主要應用場景；最后指出了現有方案面臨的一些問題以及未來的發展趨勢和研究方向。

1 累加器模型與定義

1.1 系統模型

一般來講，一個密碼累加器主要包括以下3個主體。

(1) 累加器管理員：生成密鑰對，創建并發布累加器。此外，動態累加器可以添加和刪除元素，并創建這些元素的成員證據。通用累加器可以對沒有被聚合到累加器中的元素創建非成員證據。

(2) 用戶：接受累加器管理員提供的證據，證據是他們在累加器系統中的憑證，可以提供給驗證方進行驗證。之后有新的元素添加到累加器時，用戶可以在本地更新證據。

(3) 驗證方：通過用戶提供的證據和累加器公開的累加值，來檢查元素x是否在此累加器中。

下面分別對靜態累加器、動態累加器以及通用累加器進行了定義。用X表示累加器的累加值域，用X={x1，…，xn}表示累加器中元素的集合，用t表示累加元素的上限，t可以是無窮的，表示累加域無界。此外，陷門信息(即私鑰skacc)是可選擇的輸入，因為有些累加器需要陷門信息才能更新累加器或證據，而有些不需要。

定義1一個靜態累加器方案可以描述成一個四元組Π=(Gen，Eval，WitCreate，Ver)。

(1) Gen(1λ，t)：累加器管理員輸入安全參數λ、累加元素上限t，輸出密鑰對(skacc，pkacc)，如果累加器不存在陷門信息，則陷門信息skacc=φ。

(2) Eval((skacc，pkacc)，X)：累加器管理員計算累加值和輔助信息。輸入集合、密鑰對(skacc，pkacc)，輸出累加值accX，并將其公布給用戶和驗證方；輸出輔助信息aux，并發送給用戶，使得用戶可以在本地更新證據。

(3) WitCreate((skacc，pkacc)，xi，accX，aux)：累加器管理員創建用戶xi的證據。輸入密鑰對(skacc，pkacc)、累加值accX、元素xi∈X及輔助信息aux，生成xi的證據wi。

(4) Ver(pkacc，xi，wi，accX)：驗證方驗證元素是否在累加器中。輸入公鑰pkacc、累加值accX、元素xi及其證據wi。如果wi是xi∈X的證據，則返回1；否則，返回0。

在此基礎上，如果累加器可以動態地更新集合X，并可以有效地更新集合中元素的證據，那么該累加器為動態累加器。通過對靜態累加器定義擴展，可以得到一個動態累加器。

定義2動態累加器在靜態累加器的基礎上添加了一個三元組Π=(Add，Del，MemWitUp)。

(1) Add((skacc，pkacc)，accX，aux，x)：累加器管理員添加元素x?X到累加器中，并更新累加值accX。輸入密鑰對(skacc，pkacc)、累加值accX、輔助信息aux和要添加的元素x?X，輸出更新后的累加值accX′=accX∪{x}，并更新輔助信息aux。

(2) Del((skacc，pkacc)，accX，x，aux)：累加器管理員刪除元素x∈X時，更新累加值accX。輸入密鑰對(skacc，pkacc)、累加值accX、輔助信息aux和被刪除的元素x∈X，輸出更新后的累加值accX′=accX{x}，并更新輔助信息aux。

(3) MemWitUp((skacc，pkacc)，x，wi，aux)：添加或刪除元素x后，用戶更新元素xi的證據wi。輸入密鑰對(skacc，pkacc)、x、輔助信息aux和xi的證據wi，輸出xi更新后的證據w′i。

上述累加器可以對元素x∈X構造成員證據，但無法對元素x?X構造非成員證據。而通用累加器既可以對元素x∈X構造成員證據，又可以對元素x?X構造非成員證據。

定義3通用累加器在上述WitCreate算法中，可以添加一個布爾參數type，創建成員證據時type=0，創建非成員證據時type=1。如果通用累加器不具備動態累加器添加或刪除元素的功能，則為通用靜態累加器，否則為通用動態累加器。對于通用動態累加器，則需要在定義1和定義2的基礎上添加NonMemWitUp算法，可以在累加集合更新時，對非成員證據進行更新。

(1) NonMemWitUp((skacc，pkacc)，x，w，aux)：在添加或刪除某個元素x時，用戶更新非成員元素y?X的證據u為u′。輸入密鑰對(skacc，pkacc)、x、輔助信息aux和y的證據u，輸出y更新后的證據u′。

1.2 累加器的性質

累加器有3個安全性質：正確性、健壯性(包括無碰撞性和不可否認性)、不可區分性。3個安全性質定義如下：

(1) 正確性：對于所有誠實生成的密鑰、所有誠實計算的累加值和證據，驗證算法Ver將始終返回1。

(2) 健壯性：傳統上，健壯性指無碰撞性，對于元素y?X，很難找到其成員證據[8]，對于元素xi∈X，也很難找到其非成員證據[7]；健壯性的另一種擴展形式是不可否認性[23]，不可否認性是通用累加器特有的性質，它表示為元素x∈X或x?X計算兩個相互矛盾的證據在計算上是不可能的。

(3) 不可區分性：不可區分性[25-26]與安全隱私相關，指累加器和持有證據的用戶都不會泄露有關累加集合X的信息。

分別對靜態累加器、動態累加器和通用累加器進行形式化定義。具體如下：

(1) 安全性(靜態)：一個靜態累加器是安全的，如果對于所有概率多項式時間(Probabilistic Polynomial Time，PPT)對手Aλ，有

(2) 安全性(動態)：令M為接收輸入(f，aux，g)的交互式圖靈機，其中，aux是有關f的輔助信息，g∈ZA。M維護一個元素集合X，該集合最初為空，初始累加器acc設置為g。M響應兩種消息：對于消息D(add，x)，它確保x∈X，將x添加到集合X中，通過運行D修改acc，然后將更新后的acc發回；對于消息D(delete，x)，它將檢查x∈X，將其從集合X中刪除，通過運行D更新acc，然后將更新后的acc發回。最后，M輸出X和acc的當前值。如果對于所有PPT的對手Aλ，動態通用累加器方案是安全的，則有

(3) 安全性(通用)：一個通用累加器是安全的，如果對于所有PPT對手Aλ，有

2 基于RSA體制的累加器

2.1 靜態累加器

(1) Gen(1λ)：累加器管理員輸入安全參數λ，生成累加器初始值g∈Zn，輸出密鑰對(skacc，pkacc)=((p，q)，N)，其中N由兩個大的強素數p、q組成，且N=pq。

(2) Eval(pkacc，X)：累加器管理員計算累加值。累加值accX=gx1，…，xnmodN，其中X={x1，…，xn}，且xi是素數。

(3) WitCreate(pkacc，xi，accX)：累加器管理員創建用戶的證據。輸入公鑰pkacc、累加值accX和元素xi，生成xi的證據wi=gx1，…，xi-1，xi+1，…，xnmodN。

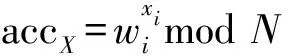
值得注意的是，RSA累加器在計算過程中需要進行模冪運算，集合X中的元素在指數中是乘法關系，所以上述構造的元素必須限制為素數，如果聚合的是非素數，則可能存在某個值是另2個值的乘積，進而敵手可以很容易偽造證據進行驗證。

2.2 動態累加器

在一些需要添加或撤銷成員的應用場景中，如在群簽名、匿名憑證撤銷系統中，群管理員需要動態添加或撤銷成員資格。然而，上述靜態累加器的集合元素固定，不具備添加或刪除的功能。因此，CAMENISCH等[6]為了解決匿名憑證系統的撤銷等問題，將累加器擴展為動態。動態累加器允許累加器管理員動態地添加或刪除元素，并且可以動態地更新累加器和成員證據。在添加元素時，更新累加器、成員證據只需要進行簡單的模指運算，可以很容易實現；而在刪除元素時，CAMENISCH等[6]采用了RSA算法的基本思想來更新累加器，通過使用陷門信息skacc進行求逆運算，可以將元素從累加器中刪除。刪除元素時需要用陷門信息更新累加值，但更新成員證據時無需陷門信息。方案具體如下：

(1) Gen(1λ)：累加器管理員生成公私鑰對，初始空累加值acc0=g∈ZN。輸入安全參數1λ，輸出累加器管理員公私鑰對(skacc，pkacc)=((p，q)，N)，其中N=pq，且p、q為大的強素數。

(2) Add(accX，x，X，pkacc)：累加器管理員添加元素x后更新累加值accX。添加元素x?X到累加器中，X更新為X∪{x}，更新后的累加值為

(3) Del(accX，x，X，(skacc，pkacc))：累加器管理員刪除元素x后更新累加值accX。刪除元素x時，需要陷門信息skacc，通過計算的累加值為

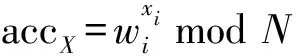
值得注意的是，執行刪除操作時，累加器管理員需要用到陷門信息skacc來更新累加值，此時不誠實的累加器管理員可以通過陷門信息隨意更改累加值、對成員創建假的證據等，所以必須要求累加器管理員是可信的。

2.3 通用累加器

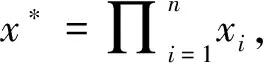
該方案給出了兩種創建非成員證據的方法，一種需要陷門信息skacc，另一種不需要。不需要陷門信息的方法在計算非成員證據時需要找到a、b，使得ax*+byi=1，而x*與累加器成員個數線性相關，計算開銷很大。需要陷門信息的方法在計算證據時，可通過x*′=x*mod(p-1)(q-1)，其中p、q為陷門信息，使得x*′在進行模運算后很小，從而在ax*′+byi=1中，證據的計算開銷僅為O(1)。因此在某些可以使用陷門信息的場景下，選擇需要陷門信息計算非成員證據的計算量小；而對于某些無法使用陷門信息的場景下，不需要陷門信息計算非成員證據是一個很好的選擇。下面給出了兩種計算非成員證據的具體構造。

2.3.1 需要陷門信息

使用skacc計算非成員證據。假設存在受信任的累加器管理員知道skacc=(p，q)、集合X={x1，…，xn}、累加器accX=gx1，…，xnmodN，其中g∈QRN。累加器管理員計算元素yi?X的非成員證據如下：

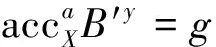
2.3.2 不需要陷門信息

該方案同時支持元素的動態添加和刪除，并實現相應證據的高效更新，具體的非成員證據更新算法NonMemWitUp如下：

NonMemWitUp(x，(a，B)，accX，accX′)：

添加：添加元素x∈XX，且x≠yi，給定更新前后的累加器accX和accX′，則yi∈XX的證據ui=(a，B)更新如下：

(1) 找到兩個整數a0′和r0，使得a0′x+r0yi=1，由于x、yi都為素數，所以a0′、r0可以很容易找到；

(2) 兩邊同乘更新前的證據a，使得a0′ax+r0ayi=a；

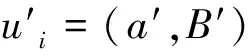
(1) 選擇一個整數r，使得ax-ryi∈Z2l；

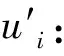
2.4 支持批處理更新的累加器

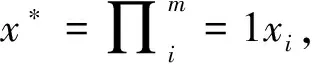
LI等[7]簡要地概述了累加器可以批量添加和刪除元素，并未給出具體的算法，而BONEH等[19]給出了具體的批量添加(BatchAdd)和批量刪除(BatchDel)的算法。在BatchDel中，存在一個ShamirTrick算法，可以將兩個元素的證據聚合在一起。具體的算法如下：

(1) BatchAdd(accX，{x1，…，xm})

② accX′←accx*

(2) BatchDel(accX，(x1，w1)…(xm，wm))

① accX′←w1

②x*←x1

③ fori←2，i≤m

④ accX′←ShamirTrick(accX′，wi，x*，xi)

⑤x*←x*·xi

⑥ return accX′

(3) ShamirTrick(w1，w2，x1，x2)

②a，b←Bezout(x1，x2)

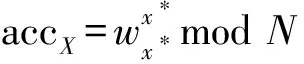
PoE協議輸入：u、w∈G，x∈Z；證明：ux=w。

① 驗證方發送隨機的λ比特的素數l給證明方；

② 證明方計算(q，r)，使得x=ql+r，并將Q=uq發送給驗證方；

③ 驗證方計算r=xmodl，當Qlur=w成立時接受。

此外，為了減小通信開銷，BONEH等[19]也使用了Fiat-Shamir啟發式方法[32]及多輪協議的概括[33]，將PoE協議改成了非交互式協議NI-PoE。并將NI-PoE協議運用到累加器中來提高批處理成員驗證的效率，具體構造如下：

MemWitCreate*(accX，{x1，…，xn})

②wx*←WitCreate(accX，x*)

③ returnwx*，π=NI-PoE(x*，wx*，accX)

VerMem*(accX，{x1，…，xn}，w={wx*，π})

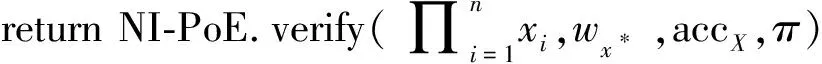
除了成員驗證效率得到了提高，非成員驗證的效率也提高了。當進行批處理非成員驗證時，一種方法是通過NonMemWitCreate*算法將多個非成員元素直接相乘來創建證據，驗證時只需要驗證VerNonMem*算法中的協議運行是否成功。另一種方法是通過AggNonMemWit算法聚合這些非成員證據來創建證據。

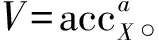
PoKE2協議輸入：u、w∈G；證據：x∈Z；證明：ux=w。

① 驗證方發送g給證明方；

② 證明方發送z=gx給驗證方；

③ 驗證方發送隨機的λ比特的素數l和一個挑戰值α給證明方；

④ 證明方計算(q，r)，使得x=ql+r，并將Q=uqgαq和r發送給驗證方；

⑤ 驗證方檢查Qlurgαr=wzα是否成立。

NonMemWitCreate*(accX，x*，y*)：//accX=gx*，x*=∏x∈Xx，y∈∏yi

①a，b←Bezout(x*，y*)//ax*+by*=1

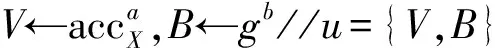
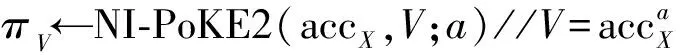
④πg←NI-PoE(y*，B，gV-1)//By*=gV-1

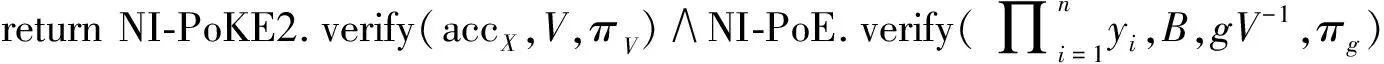
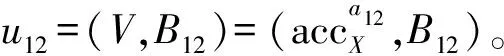
①a，b←Bezout(y1，y2)

③a′←ba1y2+aa2y1

④a12←a′mody1y2

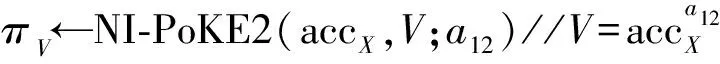
⑧πg←NI-PoE(y12，B12，gV-1)//By1212=gV-1，y12=y1y2，

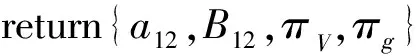
3 基于雙線性映射的累加器

RSA累加器方案中，累加器聚合的元素被限制為素數，需要把元素轉變為素數[34]后才能進行累加。為了解決這個問題，NGUYEN等[9]首次提出了基于強Diffie-Hellman(SDH)假設的雙線性映射動態累加器，此累加器不要求累加值域為素數。DAMGARD等[10]和AU等[11]補充了LI等[7]提出的通用累加器構造，使得雙線性映射累加器同RSA累加器一樣，都具備了動態和通用的功能。然而，上述累加器中累加集合的大小需提前設定，如累加的元素數量上限為q。因此，TOLGA等[35]通過一組累加器突破了上述累加集合大小受限的問題。此外，CAMENISCH等[12]也給出了一種基于q-DHE假設的方案，此方案對證據和累加器的更新無需陷門參與，即支持公開更新。

3.1 動態累加器

RSA累加器的累加域元素要求為素數，為了解決這一問題，NGUYEN等[9]提出了基于q-SDH假設的雙線性映射累加器，其中累加的元素的數量上限為q。相比于RSA累加器采用模冪運算聚合累加元素，此構造以雙線性對運算為基礎。具體構造如下：

(2) Eval(X，pkacc)：累加器管理員計算累加值accX。輸入集合X={x1，…，xn}?Zp{-s}，其中n≤q，使用pkacc而無需私鑰s的情況下計算累加器accX=gu∏x∈X(x+s)。

(3) WitCreate(pkacc，xi，accX，X)：累加器管理員創建用戶xi的證據。輸入公鑰pkacc、累加值accX、集合X和元素xi，生成xi∈X的證據為wi=gu∏x∈X{xi}(x+s)。

(4) VerMem(accX，xi，wi)：驗證方驗證xi是否在累加器中。通過驗證e(wi，gxigs)=e(accX，g)是否成立。如果成立，則輸出1，否則輸出0。

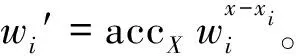
要注意的是，在上述構造中，公鑰大小與累加元素的上限q線性相關，如果q很大，則元素公鑰將會非常大，而在RSA累加器中，公鑰是常數N。此外，RSA動態累加器只有在刪除操作更新累加值時會用到陷門信息skacc，而在此構造中，更新累加值時，包括添加和刪除都需要用到陷門信息。

雙線性映射動態累加器除了該基于q-SDH假設的方案之外，CAMENISCH等[12]也給出了一種基于q-DHE假設的構造。此方案采用了兩個公開的集合V和Vw，分別是被累加到累加器中的元素集合和證據wi被創建時，累加器添加或刪除了哪些元素的集合。當證據需要更新時，可以通過Vw對所有元素的證據公開更新。具體構造如下：

(1) Gen(1λ，t)：輸入參數1λ和累加元素上限t，累加器管理員隨機選擇值γ∈Zq，生成初始累加器accφ=1、初始狀態stateφ=(φ，gγ1，…，gγq，gγq+2，…，gγ2q)和公私鑰對：

(pkacc，skacc)=((g1，…，gq，gq+2，…，g2q，e(g，g)γq+1，pksig)，(γ，sksig))=
((gγ1，…，gγq，gγq+2，…，gγ2q，e(g，g)γq+1，pksig)，(γ，sksig)) 。

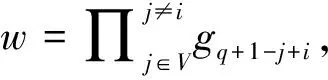
stateU∪{i}={U∪{i}，g1，…，gn，gn+2，…，g2n} 。

(3) Update(pkacc，V，stateU)：用戶輸出accV=∏v∈Vgn+1-v(V?U)。

(4) WitUp(pkacc，wi，Vw，V，accV，stateU)：任何不可信實體都可以進行證據的更新。如果i∈V且V∪Vw?U，計算

輸出wi′=(w′，σi，gi)。

(5) VerMem(pkacc，i，wi，accV)：驗證方驗證i是否在累加器中。不可信實體更新證據wi后，用戶i獲得新的證據wi′后，通過等式e(gi，accV)=ze(g，w)來驗證i是否在累加器中。

在刪除成員時，RSA累加器[6-7]和基于SDH假設的雙線性映射累加器[9-10]更新累加值都會用到陷門信息，并且更新操作都進行了冪運算。而該方案在刪除成員時更新累加器不需要陷門信息，并且更新操作無需進行冪運算，只用進行簡單的乘法運算，因此計算效率大大提升。

3.2 通用累加器

上述累加器無法支持非成員驗證，因此，DAMGARD等[10]首次基于SDH假設將雙線性映射累加器擴展為通用累加器，具體非成員證據的構造和驗證方法如下：

(2) VerNonMem(accX，y，(ay，By))：驗證方驗證元素y的非成員身份。已知公共參數gs，驗證通過檢查e(ay，gygs)=e(accXgBy，g)是否成立。如果成立，則輸出1，否則輸出0。

在該方案的基礎上，AU等[11]也提出了基于SDH假設的通用累加器方案，使得無需使用陷門信息便可進行累加器的更新。

4 基于Merkle哈希樹的累加器

Merkle哈希樹累加器是一類設計簡潔且高效的累加器。Merkle哈希樹中，葉子節點為集合元素的哈希值，內部節點為左右孩子的哈希值，根節點為最終累加值。元素xi的成員證據由xi到根節點路徑上的所有兄弟節點組成，通過重構根節點來判斷元素xi是否存在于集合中。然而，RSA累加器和雙線性映射累加器只需O(1)大小的證據，而Merkle哈希樹累加器需要O(logN)大小的證據，其中N表示累加元素的總數。

CAMACHO等[13]給出了一個通用累加器方案的簡單構造，該方案和LI等[7]的通用累加器方案在功能上是相似的，適用于動態集合并允許非成員身份證明，并且該方案在存在抗碰撞哈希函數的假設下可證明是安全的。該方案實現非成員證明的主要思想為：集合中元素按順序存儲，若某元素的左右相鄰元素為連續元素，則該元素不在集合中。例如，x的左右相鄰元素為xα、xβ，且xα、xβ連續，則x為非成員元素。方案具體構造如下：

(1) Gen(1λ)：累加器管理員輸入安全參數λ，生成初始累加器acc0和M0。初始集合X為空，是M={0，1}λ的子集；然后選擇一個哈希函數H，計算一個隨機索引i∈K，并設置H=Hi；最后將m的初始值設置為H(-∞‖+∞)的根節點Nm，并且累加器管理員公布acc0=ProofNm。

(2) WitCreate(m，x)：累加器管理員創建證據。輸入x∈M和內存m，計算證據w=(w1，w2)如下：

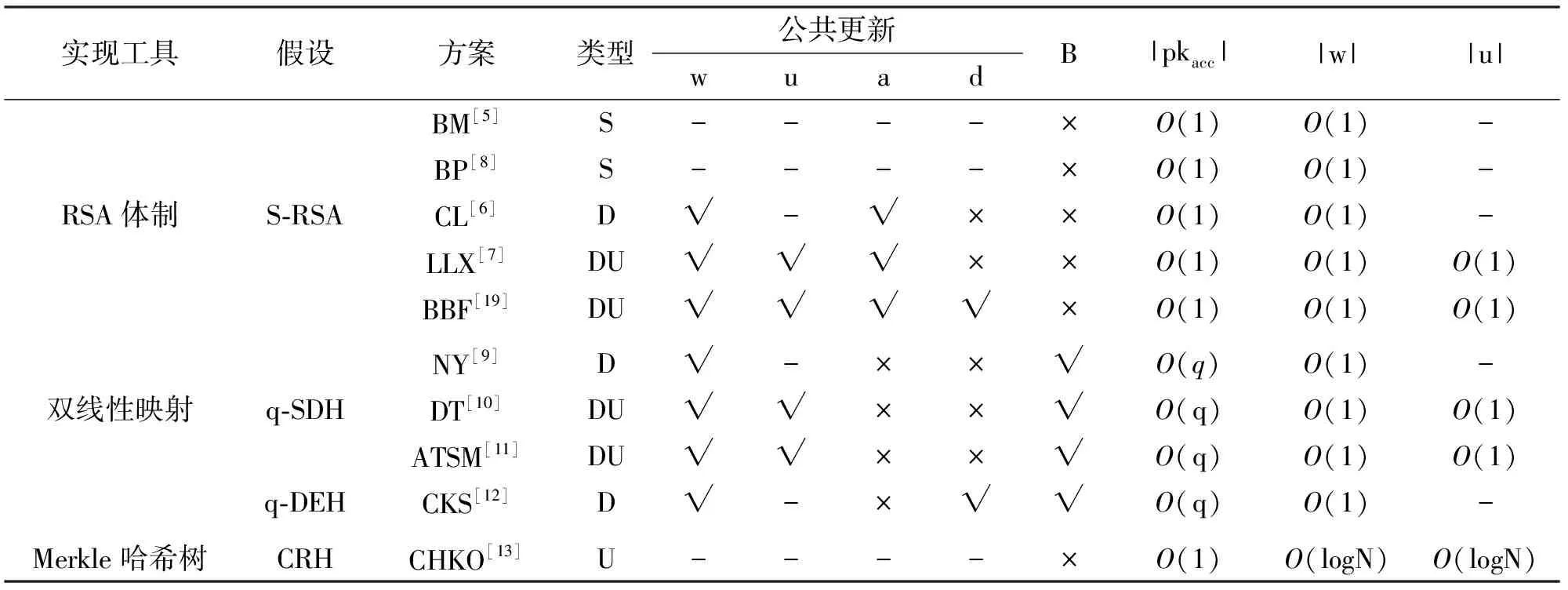
① 如果x∈X，則證據w1=(xα，xβ)，其中x=xα或x=xβ；否則x?X，證據w1=(xα，xβ)，其中xα

② 設置w2是由H(xα‖xβ)生成的m的最小子樹。

(3) Update(m，x)：累加器管理員更新累加器、內存m和證據w。輸入x∈X，acc和m。

① 添加：x?X時，添加x操作如下：將m中適當節點處的值H(xα‖xβ)替換為H(xα‖x)，其中xα

② 刪除：刪除x時，查找包含x的兩個節點，用Vα，Vβ表示。刪除x后，用H(xα‖xβ)代替之前的H(xα‖x)和H(x‖xβ)，并保持樹平衡。更新后的樹為m′、累加器acc′=Proofm′、證據w′=(del，w1，w2，w3)。

(4) CheckUpdate(acc，acc′，w′)：在添加或刪除元素后，用戶檢查累加器管理員提供的更新后的元素，更新正確，則輸出OK。輸入x∈M、更新前的累加器acc、更新后的累加器acc′和更新后的證據w′。如果w′=(add，w1，w2)且符合下列前提，則算法輸出1；否則輸出0。刪除操作也類似，這里省略。

①w1是通過在w2上添加葉子獲得的樹。

② 除了值是H(xα‖xβ)的節點以外，w1、w2樹中其余所有節點都相同。

③ Proofw1=acc，Proofw2=acc′。

④H(xα‖x)，H(x‖xβ)∈Vw2。

(5) VerMem(x，w，acc)：驗證方驗證某個元素是否在集合中。輸入x∈M、證據w=((w1，w2)，u)和累加器acc。檢查(a)Proofu=acc；(b)H(x′‖x″)∈Vu和(c)(x=x′)，(c)(x=x″)或(c′)(x′

首先，在RSA累加器和雙線性映射累加器中，需要累加器管理員生成陷門信息來更新累加器或證據，而Merkle哈希樹累加器[13]不需要陷門信息來更新累加器或證據，因而無需管理員參與。其次，Merkle哈希樹累加器主要基于哈希算法，而RSA累加器和雙線性映射累加器分別需要模指數運算和雙線性對運算，所以Merkle哈希樹累加器計算效率高。然而，Merkle哈希樹累加器的證據大小與集合大小呈對數關系，所以通信代價較高。

5 三類密碼累加器的分析與比較

對上述3類密碼累加器的構造方案進行了比較和總結。RSA累加器基于強RSA假設，具有較短的公共參數，且可以很容易擴展到通用累加器[7]或動態累加器[6]，但此類型下的累加器通常需要昂貴的操作才能將元素以素數形式編碼。雙線性映射累加器有基于q-SDH假設和q-DHE假設的兩種類型，它們不需要素數編碼，但需要最大元素數量的公共參數。大多數RSA累加器和雙線性映射累加器都需要可信累加器管理員生成陷門信息。如在RSA累加器中，任何知道模N=pq分解的對手都可以輕易地作弊。而Merkle哈希樹累加器不需要陷門信息，把這類不需要陷門信息的累加器也稱為強累加器。Merkle哈希樹累加器基于抗碰撞的哈希函數假設，是一類高效簡潔的累加器，但是該類構造不需要可信的累加器管理員，所以需要O(logN)大小的證據(N表示累加集合的元素數量)，而前兩類需要可信設置的累加器只需O(1)大小的證據。此外，RSA累加器和雙線性映射累加器也有一些構造[23，28]。這些構造下，累加器管理員完全不受信任，但這些構造要么證據數量隨集合X的大小呈對數增長，要么依賴尚未在密碼學進行深入研究的代數群。

表1給出了3類密碼累加器構造方案的詳細比較[26，36]。其中，S代表靜態累加器，D代表動態累加器，U代表通用累加器，w代表成員證據的更新，u代表非成員證據的更新，a和d分別代表添加和刪除操作時累加值的更新，acc代表累加值的更新，B代表累加器累加元素是否具有上限，|pkacc|、|w|、|u|分別代表公共參數，成員證據和非成員證據的大小。

表1 不同類型累加器的比較

6 應 用

累加器自提出以來，有著廣泛的應用場景。包括時間戳[5]、群簽名[6，37]、環簽名[38]、訪問控制系統[39]、匿名憑證系統[6]、加密貨幣[19]、認證數據結構(ADS)[15-18]等。此外，還被用在隱私保護數據外包[20]、認證字典[21]、編輯[22]、負責任的證書管理[23-24]等應用中。介紹幾種典型應用：累加器在時間戳、成員資格撤銷中的應用。此外，還會介紹最近比較流行的應用：累加器在區塊鏈[40-42]中的應用。

6.1 時間戳

BENALOH等[5]首次提出了密碼學累加器，并應用于時間戳中。時間戳可以在任何文檔上附加一個“發布”日期，以證明原始文件在簽名時間之前已經存在。在傳統的時間戳系統中，機構需要對文件逐個添加時間戳，驗證方也需要逐個驗證，使得時間戳的生成和驗證代價高。為了提高時間戳系統的效率，BENALOH等[5]設計了基于密碼累加器的時間戳系統，該系統可以批量的生成和驗證時間戳。具體方法為：將某個時刻產生的所有文檔聚合到累加器中，然后對該累加器附加時間戳。驗證t時刻的文檔時，僅需驗證該文檔存在于t時刻的累加器中，并且可以實現多個文檔時間戳的批量驗證，大大提高了時間戳系統的生成和驗證效率。

6.2 成員資格撤銷

靜態累加器[5]可以用來解決時間戳、成員資格測試等集合成員無需變動的問題。然而，存在一些應用場景需要對成員進行添加或刪除操作，如匿名憑證撤銷系統、群簽名方案、身份托管方案等[43-45]會進行撤銷成員的操作。傳統的撤銷方案[43]如下：一種是當用戶嘗試訪問資源時，驗證方通過在數據庫中查找用戶的證書，使得證書被撤銷的用戶無法訪問資源，但此查詢操作與用戶數線性相關；另一種方法是每天為所有合格用戶重新頒發新的證書，使得證書被撤銷的用戶無法使用舊證書訪問資源，此方法中，合法用戶進行證書驗證和管理員重新頒發證書的通信成本高，與成員數線性相關。上述撤銷方案的困難度與合法成員數線性相關。為了解決此類撤銷問題，CAMENISCH等[6]提出了基于動態累加器的成員撤銷系統。在該方案中，群管理員充當累加器管理員的角色，將合法證書聚合成累加值。當撤銷成員時，群管理員用累加器陷門信息更新累加值。由于動態累加器在撤銷證書時，更新累加值和證據的計算量與合格成員數和撤銷用戶數量無關，所以大大提高了成員資格撤銷的效率。

6.3 無狀態區塊鏈

近年來，區塊鏈的擴容技術[19，40，46-47]有很多，其中無狀態區塊鏈[19]是一項很重要的擴容技術。如在比特幣中，當節點A向B發起一筆轉賬時，除了需要通過簽名來驗證這筆交易是否是A發起的，還要驗證A是否有這筆錢。在傳統驗證方法中，驗證節點維護網絡中每個節點的未花費交易集合UTXO[19]，驗證節點通過查看節點A發起的交易是否在UTXO集合中來判斷A是否發起了合法的轉賬。然而，隨著參與比特幣交易的用戶越來越多，UTXO集合越來越大，驗證節點的存儲壓力也越來越大。除了比特幣等基于UTXO模型的區塊鏈面臨這樣的問題，基于賬戶的模型，如以太坊也面臨著同樣的問題。為了解決此類問題，BONEH等[19]提出了基于支持批處理累加器的無狀態區塊鏈。在該無狀態區塊鏈的構造中，驗證節點無需存儲整個UTXO集合，只需存儲該UTXO集合中元素的累加值，用戶節點存儲與自己相關的UTXO及證據。當進行一筆交易時，交易發起者會提供附帶證據的交易給驗證節點，驗證節點通過判斷交易和證據是否通過驗證來確定這筆交易是否合法。此外，批處理累加器可以對交易進行高效批量驗證，不僅減輕了全節點的存儲壓力，而且進一步提高了驗證效率。在此之后，也產生了很多區塊鏈擴容技術[19，40，46，47]。

7 總結和展望

筆者主要圍繞密碼累加器的相關研究內容展開綜述，并按實現方式、功能對累加器進行了分類，詳細描述了基于RSA的累加器、基于雙線性映射的累加器和基于Merkle哈希樹的累加器的經典構造。經過分析，現有的累加器方案仍然存在一些不足，未來的研究方向可以關注以下幾點：

(1)基于雙線性對的累加器解決了累加元素必須為素數的不足，然而，該類累加器的公開參數的大小與集合的大小相同，增加了通信代價。此外，累加器的大小需提前設置，即累加器包含的元素個數固定。在動態應用場景中，元素的個數不斷增加，若參數設置過大，則增加公開參數的傳輸開銷；若參數設置過小，則應用場景受限。因此，如何突破雙線性映射累加器的大小限制成為未來研究的方向之一。

(2)在可驗證外包數據存儲中，使用數字簽名、布隆過濾器、Merkle哈希樹等驗證數據結構驗證外包數據的完整性，具有證據生成和驗證效率高等優點。然而，該類數據驗證結構為私有驗證，即只有擁有私鑰的用戶才能驗證結構，使得使用場景受限。向量承諾、密碼累加器可以實現公開驗證，然而，構造和驗證效率低下。因此，如何構造高效的密碼累加器，應用于動態密文檢索、無狀態區塊鏈、分布式存儲系統是未來研究的方向之一。