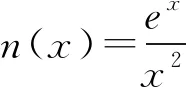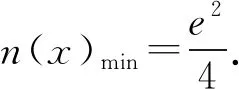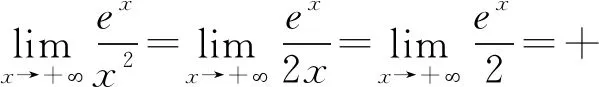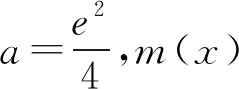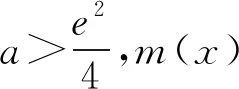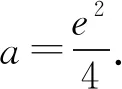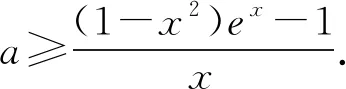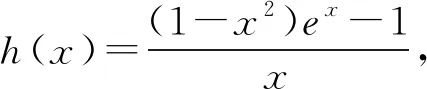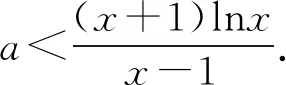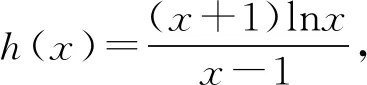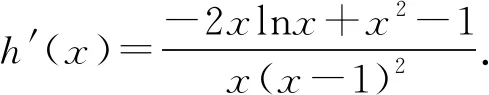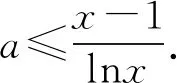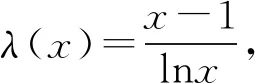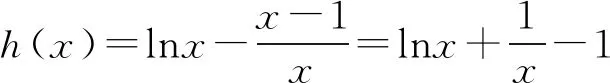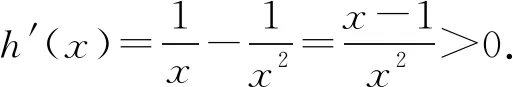一類以導數為背景的高考題的解法研究
李昌成
(新疆烏魯木齊市第八中學 830002)
多年來,數學高考卷無論文科還是理科,無論是地方卷還是全國卷,均以導數作為壓軸題.題目通常難度較大,僅僅依靠高中所學的導數知識,解答經常擱淺.很多函數問題均可等價轉化后,多次構造新函數,再多次求導,利用洛必達法則求端點臨界函數值的“最值”,最后得到參數的范圍.下面我們分類展示一些經典高考題.
類型1 分離參數構造函數后,用洛必達法則保障范圍的完整性.
例1 (2018年全國高考Ⅱ卷理科21題)已知函數f(x)=ex-ax2.若f(x)在(0,+∞)只有一個零點,求a.
解析由零點概念知,f(x)只有一個零點就是f(x)=0只有一個解.即ex-ax2=0只有一個解.
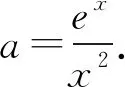
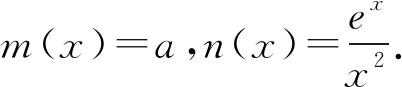
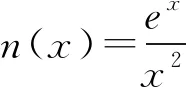
當x>2時,n′(x)>0,
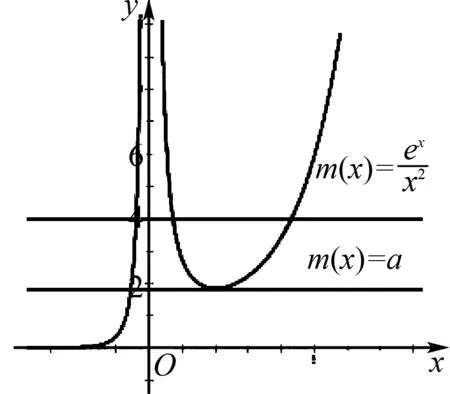
當0 (*) 如圖1,當x→0時,x2→0,ex→1, 圖1 所以n(x)→+∞. 評注這種解法只需要學生對洛必達法則有一定認識就可以掌握,整個流程邏輯嚴謹、思維連貫、順理成章.這類題目的結構相對穩定.值得一提的是,很多學生會將(*)以后的解題過程忽略,這是不嚴謹的,為什么呢?請讀者思考. 類型2 分離參數構造函數,多次求導,用洛必達法則求新函數最小值的臨界值. 例2 (2017年全國高考Ⅱ卷文科21題) 設函數f(x)=(1-x2)ex.當x≥0時,f(x)≤ax+1,求a的取值范圍. 解析當x=0時,a可取任何實數. 當x>0時,f(x)≤ax+1, 對h(x)求導,得 再令g(x)=ex(-x3-x2+x-1)+1, 對g(x)求導,得 g′(x)=ex(-x3-4x2-x). 當x>0時,g′(x)<0, 因此g(x)在(0,+∞)上單調遞減. 所以h(x)的最大值臨界值為h(0). 由洛必達法則,得 所以a的取值范圍是[1,+∞). 評注分離參數后,通過多次求導,逐層判斷單調性,最后借助洛必達法則求得端點值得到參數取值范圍,思路簡潔.本題高考給出的答案高深莫測,邏輯上讓中學生難以接受,尤其是分類討論的標準不易理解.有興趣的同仁可以查閱對比研究. 類型3分離參數構造函數,多次求導,用洛必達法則求最大值臨界值. 例3(2016年全國高考Ⅱ卷文科20題)已知函數f(x)=(x+1)lnx-a(x-1).若當x∈(1,+∞)時,f(x)>0,求a的取值范圍. 解析f(x)>0,即(x+1)lnx-a(x-1)>0. 再設φ(x)=-2xlnx+x2-1, 則φ′(x)=-2lnx-2+2x, 由于x>1,所以φ″(x)>0, 于是φ′(x)在(1,+∞)上單調遞增, 所以φ′(x)>φ′(1)=0, 進而φ(x)在(1,+∞)上單調遞增, 所以φ(x)>φ(1)=0,因此h′(x)>0, 進而h(x)在(1,+∞)上單調遞增, 所以h(x)>h(1). 所以a的取值范圍是(-∞,2]. 類型4分類討論,分離參數構造函數,用洛必達法則求最大值和最小值的臨界值. 例4(2017年全國高考Ⅲ卷理科第21題)已知函數f(x)=x-1-alnx.若f(x)≥0,求a的值. 解析當x=1時,a∈R. 當x>1時,lnx>0, 于是h(x)在(1,+∞)上單調遞增. 所以h(x)>h(1)=0,因此λ′(x)>0. 所以λ(x)在(1,+∞)上單調遞增, 于是λ(x)>λ(1). 所以a≤1. 同理,當0 綜上,a=1. 評注本題與前面幾例比較,有兩個特征:一是受lnx的正負影響,不能直接分離參數,需要討論,但由于問題的“對稱性”僅需完整解答一次即可;二是表面上是求值問題,但實際上還是求范圍問題. 類型5分離參數,“遞進式”求導,用洛必達法則求最大值的臨界值. 例5(2010年全國高考Ⅱ卷理科第21題)已知函數f(x)=ex-1-x-ax2.若當x≥0時,f(x)≥0,求a的取值范圍. 解析當x=0時,a∈R. 令m(x)=(x-2)ex+x+2, 則m′(x)=(x-1)ex+1. 則m″(x)=xex. 因為x>0,所以m″(x)=xex>0. 于是m′(x)在(0,+∞)上單調遞增. 所以m′(x)>m(0)=0. 所以m(x)在(0,+∞)上單調遞增. 所以m(x)>m(0)=0,進而h′(x)>0. 評注本題求導的目的性很明確,就是要讓m″(x)=xex出現,事實上每次求導ex的系數增加1,我們可以簡稱“遞進式”求導.但是沒有發現此規律的同學可能半途而廢. 正如波利亞所說“當你找到第一個蘑菇或作出第一個發現后,再四處看看,它們總是成群生長”.這類給定范圍下的求參數范圍的導數壓軸題,只要被分離部分易于判斷其正負,就能分離參數,構造函數,多次反復求導,我們可以借助洛必達法則模式化做答,不再為思路發愁,不再為所需最值或最值的臨界值迷茫.但是,像“2020年新高考Ⅰ卷第21題:已知函數f(x)=aex-1-lnx+lna.若f(x)≥1,求a的取值范圍.”這類不易分離參數的題目,不適合用這種解法處理.