高考數學圓錐曲線解題技巧研究

姬彩生

(江蘇省徐州市第七中學 221011)

眾所周知，高考中時間緊迫，要想取得理想成績，提高圓錐曲線解題效率尤為關鍵.為避免學生在解題中少走彎路，教學中既要啟發學生認真審題，又要做好相關解題技巧的灌輸，使學生真正消化吸收，在解題中靈活應用.

1 借助相關結論解題

解答圓錐曲線習題時利用相關的結論既能保證解題的正確性，又能節省解題時間，因此，教學中應注重為學生講解有關圓錐曲線的相關結論，要求學生根據所學進行推導.同時，為學生展示結論在解題中的應用，給其留下深刻的印象，提高其利用相關結論的解題意識.

該結論可要求學生自己進行證明.

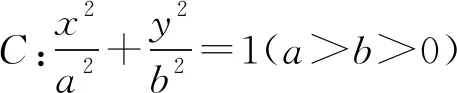
解析根據題意，設直線AP的斜率為k1，因為A(-a，0)，則其方程為y=k1(x+a).

令x=a，則y=2k1a.

則點M的坐標為(a，2k1a).

2 借助幾何知識解題

解答部分圓錐曲線習題時運用幾何知識可簡化解題過程，因此，教學中與學生一起總結與圓錐曲線相關的幾何知識，如線段的平行、垂直，三角形的相似等，并為學生展示幾何知識的應用，使其體會借助幾何知識解題的便利，為其更好地運用于解題中做好鋪墊.

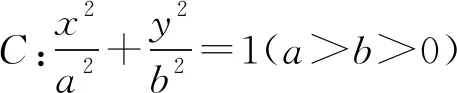
圖1

連接PF1,QM，則PF1∥QM.

所以PF1=b.

由橢圓定義可知PF=2a-b.

又因為點Q為直線PF和圓的切點，

則QM⊥PF.

所以∠F1PF=90°.

即(2a-b)2+b2=4c2.

又因為c2=a2-b2，不難得出

3 借助坐標運算解題

坐標運算是解答圓錐曲線習題的重要思路之一.教學中為使學生掌握運用坐標運算解題的技巧，應做好相關例題的優選與精講，以更好地拓展學生的解題思維，使其具體情況具體分析，選擇最優的解題方法.

設A(x0，y0)，B(x1，y1)，則D(-x1，-y1).

又因為平行四邊形ABCD的四個頂點均在該雙曲線上，所以

①

②

①-②，得

故選A.

4 借助參數方程解題

使用參數方程解答圓錐曲線習題可很好地提高解題效率.教學中應為學生講解直線以及圓錐曲線參數方程，使其明確不同參數表示的含義，更好地把握參數方程本質，尤其為學生示范參數方程在解題中的應用，使其把握相關的應用細節.

解析根據題意可設直線的參數方程為

將其和拋物線方程聯立整理，得

設A,B對應的參數為t1,t2，

高考中圓錐曲線習題類型靈活多變，解題思路也不盡相同.為提高學生解答不同題型的能力，在傳授解題技巧的同時，認真講解解題技巧的具體應用，使學生深入理解，把握相關解題技巧的細節，使其遇到相關題型，能夠快速、高效、正確求解.