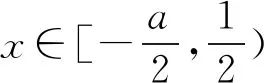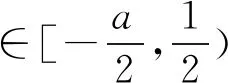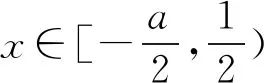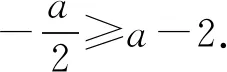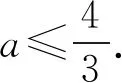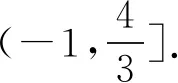從2021、2020兩年高考試題看不等式選講解題方略

游少華

(貴州省遵義市第四中學 563000)

課標卷中的兩道選作題，學生如何選擇，如何解答非常重要，甚至決定學生考試的成敗.這兩道題都體現數學的核心素養——數形結合的思想.但對不等式而言，無論是有變量問題還是定量不等式問題，學生都習慣分類討論求解.分類討論除分類不清外，還存在求交集錯誤問題，不等關系其本質上是函數圖象的上下關系.如果能作圖象解不等式，不但直觀展現大小關系，更能方便看出不等關系的變量范圍.

2021年與2020年兩年的考題都體現這一解題思想.

題1 (2021年全國文理甲卷)已知函數f(x)=|x-2|,g(x)=|2x+3|-|2x-1|．

(1)在圖1中畫出y=f(x)和y=g(x)的圖象；

(2)若f(x+a)≥g(x)，求a的取值范圍．

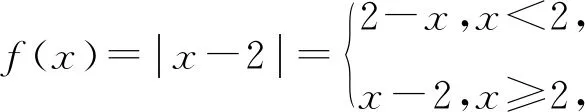
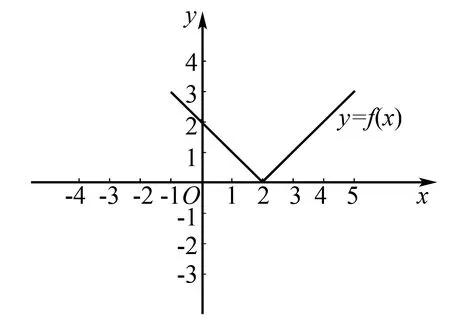
圖2

g(x)=|2x+3|-|2x-1|

畫出函數圖象如圖3：

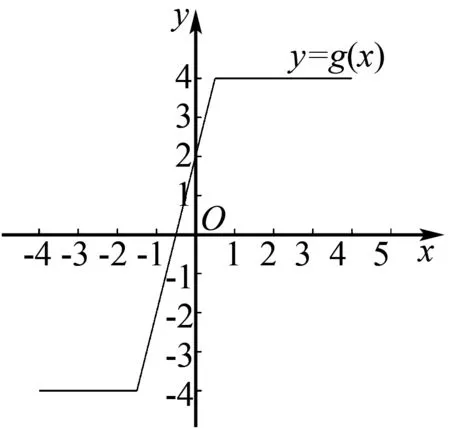
圖3

(2)f(x+a)=|x+a-2|，

如圖4，在同一個坐標系里畫出f(x),g(x)圖象，

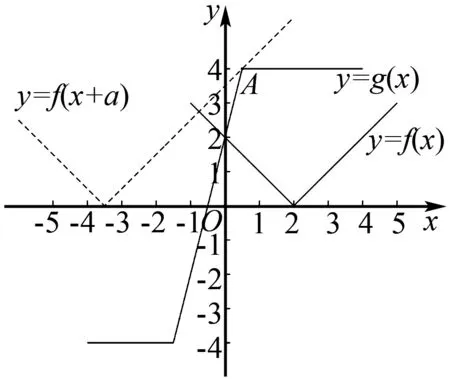
圖4

y=f(x+a)是y=f(x)平移了|a|個單位得到，

則要使f(x+a)≥g(x)，需將y=f(x)向左平移，即a>0.

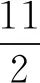
題2(2020年全國文理Ⅰ卷)已知函數f(x)=|3x+1|-2|x-1|．

(1)在圖5中畫出y=f(x)的圖象；

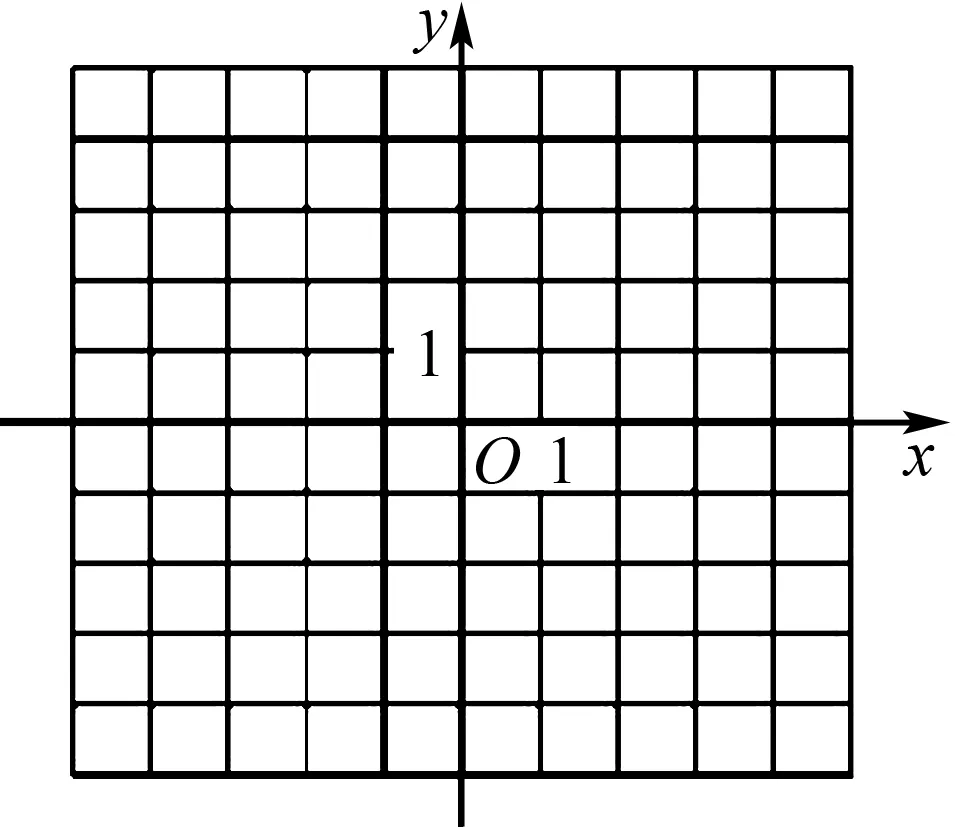
圖5

(2)求不等式f(x)>f(x+1)的解集．

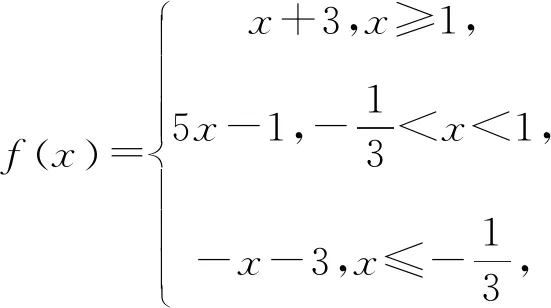
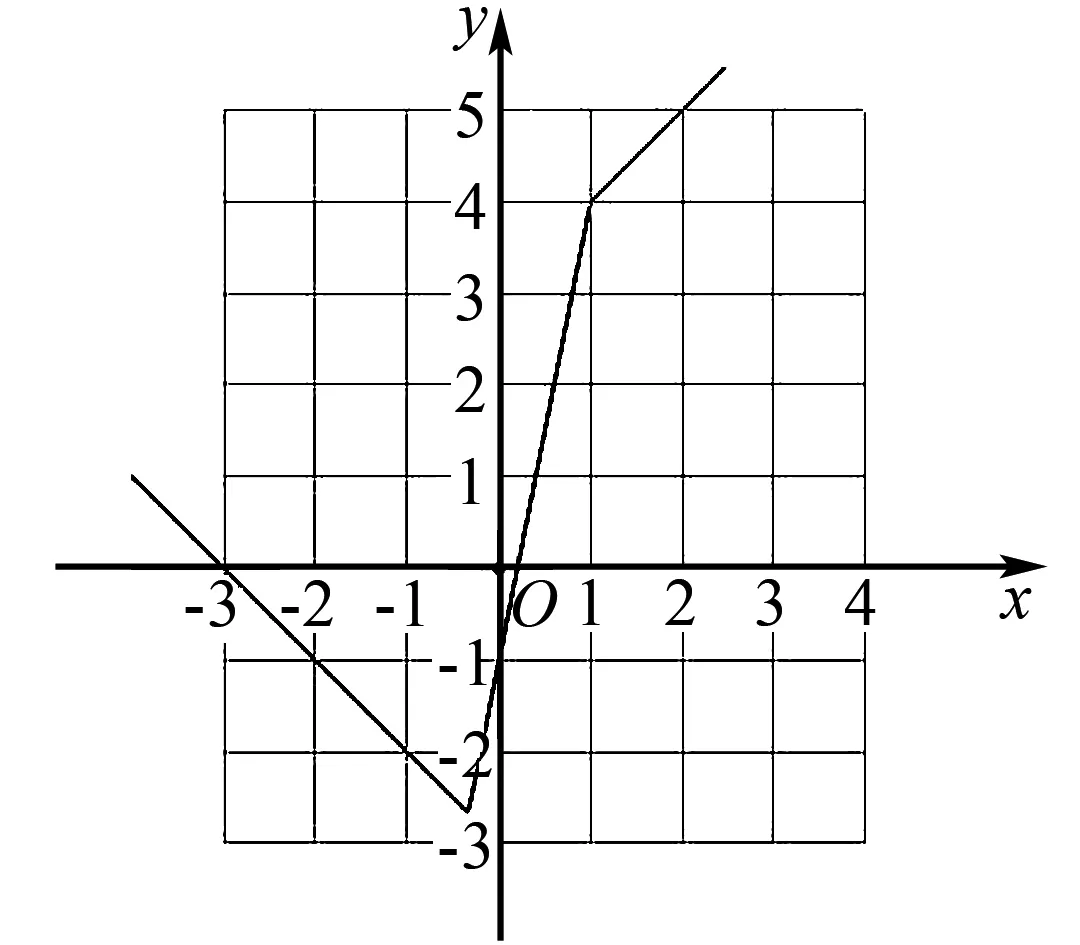
圖6

(2)將函數f(x)的圖象向左平移1個單位，可得函數f(x+1)的圖象，如圖7所示：

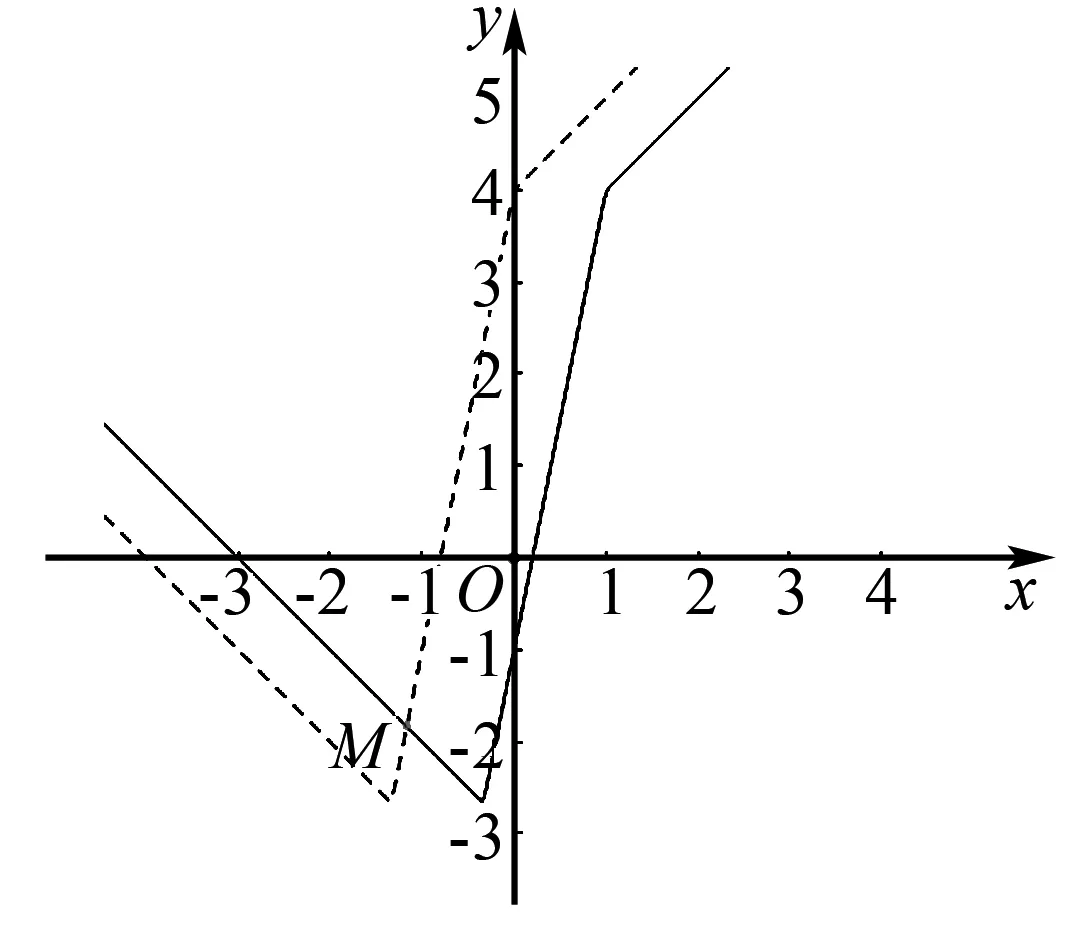
圖7

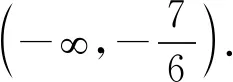
這兩年考題都是平移折線圖看變量范圍，若改為分類討論求解，就很難計算，用圖象能非常直觀地求解.在教學中應引導學生多作圖，多從圖象的上下關系去理解不等關系，學生就能從圖象移動中找到不等關系存在時的變量范圍.其實這種考題不僅在2021年與2020年出現，我們再看前些年考題，其方法都一樣，利用作圖可直接方便求解.

題3 (2018年全國Ⅲ卷文理)設函數f(x)=|2x+1|+|x-1|．

(1)在圖8中畫出y=f(x)的圖象；

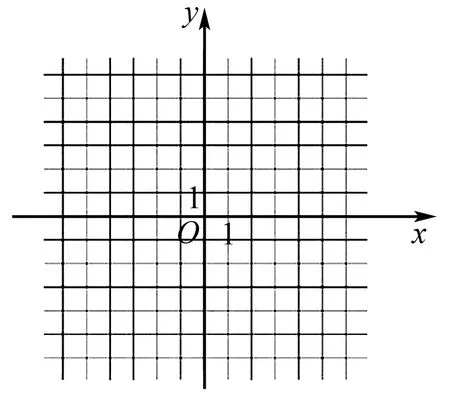
圖8

(2)當x∈[0,+∞)時，f(x)≤ax+b，求a+b的最小值．

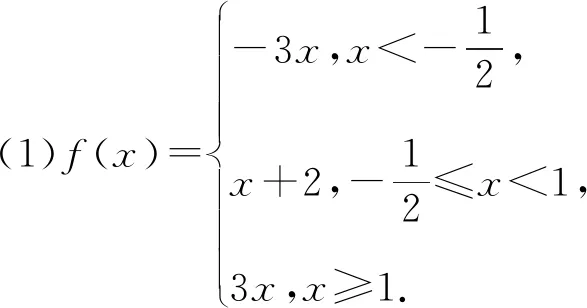
y=f(x)的圖象如圖9所示．

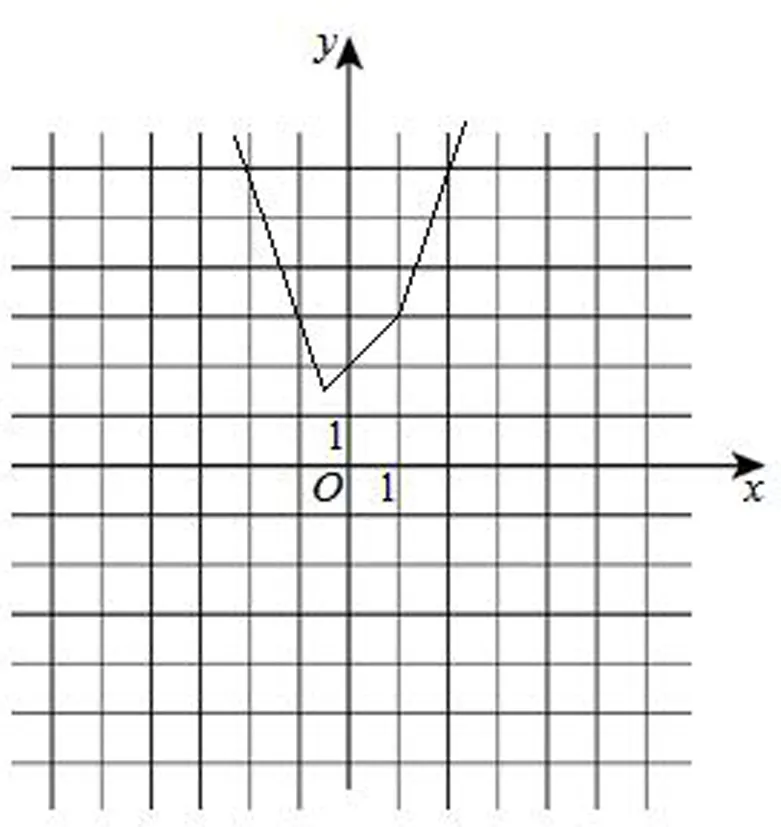
圖9

(2)由(1)知，y=f(x)的圖象與y軸交點的縱坐標為2，且各部分所在直線斜率的最大值為3.

故當且僅當a≥3且b≥2時，

f(x)≤ax+b在[0,+∞)成立，

因此a+b的最小值為5．

題4 (2013年全國Ⅰ卷文理)已知函數f(x)=|2x-1|+|2x+a|,g(x)=x+3.

(1)當a=-2時，求不等式f(x)

解析(1)當a=-2時，不等式f(x)

設函數y=|2x-1|+|2x-2|-x-3,

其圖象如圖10所示，從圖象可知，當且僅當x∈(0,2)時，y<0.

圖10

所以原不等式解集是{x|0