以導圖啟發思維 彰顯數學智慧

張鎮江

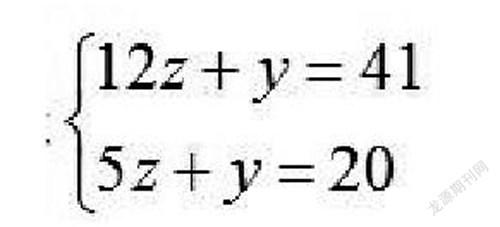
初中學生身心發展規律以及思維水平有了很大進步，為教師繼續展開數學教學奠定了基礎。然而數學知識本身具有一定的抽象性和邏輯性，需要教師在教學中善于結合學生身心發展規律以及數學知識制定相應教學策略，便于學生高效掌握數學知識點。融入思維導圖教學可以化抽象為形象，將數學知識點鏈接在一起，直觀地呈現在學生面前，有利于學生更好地理解相應知識點中的重難點，從而有效完成數學知識框架的構建。

思維導圖是一種知識網絡結構圖。它借助節點和連線來展現知識的網絡狀態。由于它具備強大的知識工具性，因此在初中數學教學中應用廣泛;除此以外，它的存在還適應初中生的身心發展規律以及思維水平特點。一方面，思維導圖憑借圖像、色彩等強大的視覺功效，將抽象的、不易理解的知識形象化展示，便于學生理解和吸收知識。另一方面，在借助思維導圖的學習中，學生可以有意識地嘗試構建相關知識的結構框架，對數學的相關概念進行整理和加工，在數學相關問題的探討中，深入理解數學知識，提高數學思維能力。

一、精準把握數學關鍵詞，構建思維導圖框架

在課堂教學中，教師可鼓勵學生把握知識中的關鍵詞，之后從數學關鍵詞出發構建完整性數學思維導圖。一方面教師以關鍵詞為抓手，以關鍵詞為思考的落腳點，引導學生對數學問題進行思考，在師生互動和生生互動中活躍氣氛，強化數學思維。另外一方面教師還應當注重尊重學生之間的差異性，設計思維導圖任務，讓不同學生結合自我實際能力完成數學思維導圖繪制任務，同時鼓勵學生之間分享與交流，查漏補缺，促進學生數學思維力的有效提升。

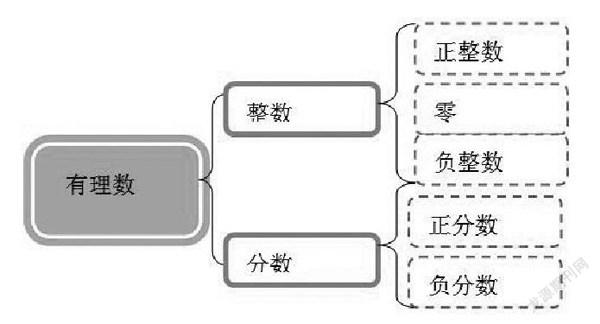
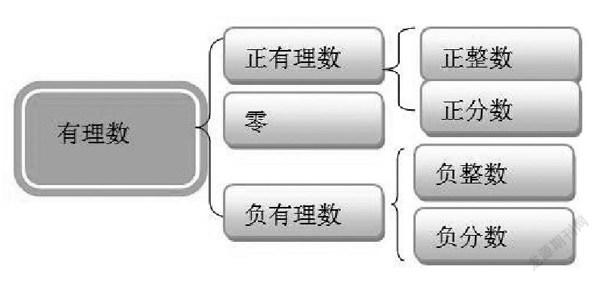
比如七年級第2章第2節《有理數和無理數》教學過程中，為了讓學生更好地掌握有理數的分類。根據定義學生抓住關鍵詞：整數和分數。教師通過和學生探討發現整數可以按照正、負的方式進行分類得：正整數、零和負整數。類比整數的分類方式學生很容易把分數進行分類。在師生探討的過程中教師利用思維導圖的形式將學生得到的結論展示出來，不僅精簡地反映了有理數的分類，同時完善了學生對有理數的認識，之后讓學生通過已有的分類進行思考，怎樣對有理數再分類？學生通過觀察發現整數和分數都可以按照正、負進行分類，從而利用類比的方法對有理數進行了再分類，通過對正、負有理數的深入認識，將正有理數和負有理數劃分不同種類，最終構建屬于自己的數學思維框架圖，具體如下

學生繪制完成有理數分類思維導圖任務之后，發現忽略了無理數，之后對于無理數進行探究，教師給學生以提示，是不是所有的數都是有理數呢？正當學生愁眉不展的時候，教師將兩個小正方形對折剪開，之后重新拼接成為一個大正方形，剪開的邊當作大正方形的邊長，其面積為“2”，大正方形的邊長為e，而e是無限不循環的小數，不能寫成分數形式，教師順利引出無理數的概念，讓學生共同回歸課本，尋找其他的無理數，比如小學時就學過的圓周率也是無理數。學生在數學知識學習中完成數學思維導圖構建任務，同時從數學關鍵詞有理數和無理數出發，進行分類與匯總，形成屬于自己的數學思維框架圖，為學生后續解決數學實際問題做好鋪墊。

二、匯總思維導圖知識，化抽象知識為形象知識

初中階段數學教師教學任務逐步從數學知識傳授轉變為學生邏輯思維力的培養。傳統教學方式直接為學生講述數學知識，會導致學生對于數學知識理解停留在機械式記憶中，無法運用所學習知識解決實際問題。融入思維導圖教學則恰好解決了當前所存在的困難，教師將部分數學知識點匯總到思維導圖中，讓學生對于抽象數學知識形成直觀性的認知，深化學生數學理解，為學生后續解決實質性問題奠定基礎。

例如在課堂教學中講授七上第4章第2節《解一元一次方程》相關知識點時，教師為學生展現方程式（1）2x+1=5，（2）3x-2=4x-3，讓學生分別將“0/1/2/3/4”代入到方程中，發現x=2，x=1，分別使得兩個等式成立，從而引出方程的解的概念。如何求解方程的解？接下來教師展示天平，利用天平表示2x+1=5的方程，結合天平的特點，組織學生將方程兩邊同時減去“1”，使得方程變成2x=4，再利用天平的特點，將兩邊同時除以“2”，最終獲得的x=2答案。當學生完成解方程的過程之后，教師提出問題，能否借助天平的特性來解釋方程的求解呢？我們可以將方程看成天平，方程兩邊的式子同時進行加減相同的數或整式，方程的解不變，這相當于天平的兩邊同時加減相同質量的砝碼，天平仍然保持平衡。同樣的天平的兩邊砝碼的質量擴大或縮小相同的倍數，天平仍能保持平衡，對應于方程的求解，容易推導出等式的基本性質即等式兩邊同時乘上或者除去一個數（除0以外），其結果是等式依然成立。最后環節中教師引領學生將所學習數學知識進行思維導圖繪制，形成直觀性數學認知，具體思維導圖展示如下：

學生匯總思維導圖知識，將解一元一次方程的過程生動呈現了出來，無論兩邊公式如何變化，只要保持同步變化，那么公式就始終保持平衡，將解一元一次方程的抽象過程轉變為直觀形象的知識，深化了學生對數學知識的認知。

三、繪制簡單有效的思維導圖，實現從特殊到一般的學習

應用思維導圖教學時，應當讓學生認識到數學知識之間本身存在一定的聯系性，面對同類型的數學問題則采取同類型的數學方法，引領學生對于數學方法進行歸類與總結，引領學生在數學學習中通過自主創新求得新知識的解決方法。同時教師在教學新知識的過程中，要善于連接舊知識，深化學生對于數學知識的感知，實現從特殊到一般的過渡，激發學生對于數學知識的探究欲望。

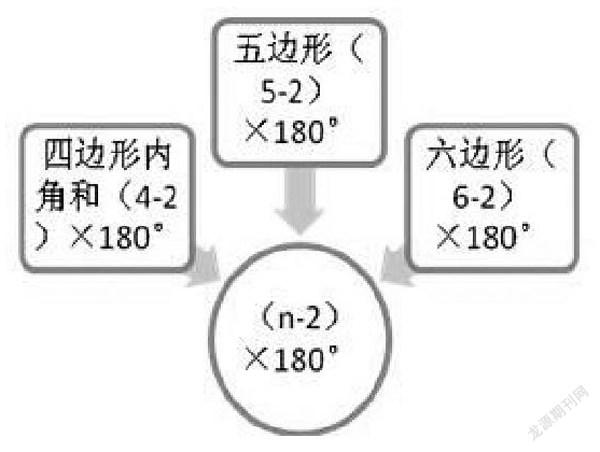
例如在七上第七章《多邊形的內角和與外角和》的教學中，為了解決多邊形的內角和知識的求解，教師提前用卡紙做三角形、四邊形、五邊形……在學生學習了多邊形的定義和多邊形的對角線知識之后，展示教具，學生分組討論如何求多邊形的內角和。通過反饋發現可以利用連接對角線，將多邊形分割成三角形，借助三角形的內角和求多邊形的內角和。從多邊形的一個頂點畫對角線，發現四邊形可以分割成兩個三角形，由三角形的內角和180°易得四邊形的的內角和為360°。之后使用相同的方法繼續探索，發現五邊形可以分割成三個三角形，六邊形可以分割成四個三角形……由此可知五邊形的內角和180°×3=540°。六邊形的內角和180°×4=720°。展示所得結果并讓學生思考六邊形、七邊形……的內角和如何求解？帶領學生總結多邊形內角求和的規律，得到n邊形內角和公式為180°（n-2）。最后將學習的多邊形內角和探究環節繪制成為思維導圖，從思維導圖視角出發，整合多邊形內角和知識，實現從特殊到一般的過渡，通過思維導圖，幫助學生更好地解決了多邊形內角和的求解問題。

四、運用思維導圖解析問題，由淺入深完成學習任務

對學生數學思維的培養已成為當前數學課堂教學中的重要課題。數學思維的建立有助于學生形成完整性數學思維框架。當學生構建了完整性數學思維框架之后，才能夠靈活性運用所學的數學知識解決問題，促進學生數學思維力的提升。初中階段數學知識則是從煩到簡，層層遞進，教師教學中重點關注數學知識難易程度，注重有層次地將數學知識展現出來，讓學生從數學知識學習中形成數學學習興趣，深化對于所學習知識的滲透，感知數學概念以及數學定理的內涵，在層層遞進中完成數學學習任務。

比如在七下第10章第4節《三元一次方程組》的教學中，要求學生會解簡單的三元一次方程組。并在解析中體會消元數學思想。首先創設教學情境“我校籃球隊參加區籃球賽，比賽規則：勝一場3分，平一場1分，負一場0分，我校籃球隊經過激烈的比賽，最終比賽22場，共得47分。比賽中獲勝的場數是負的場數的4倍多2場。求我校球隊的比賽情況”，通過分析發現有三個未知量，且找到了三個等量關系。設勝x場，平y場，負z場，可得

通過探究得出一個三元一次方程組，讓學生進行小組討論可知使用代入法可消去其中一個未知數而得到一個二元一次方程

然后通過加減得到7z=21，根據z=3代入方程組得方程組的解

通過對三元一次方程組的求解，學生發現解題的關鍵還是消元。和二元一次方程組一樣，使用加減法或代入法，將三元的方程組轉變成二元方程組再轉化為一元一次方程。最終求得答案。引領學生在層層遞進中完成三元一次方程組的學習任務，習得初步運算技能。

綜上所述，思維導圖的使用，不僅可以形象地加深學生對相關知識點的認識，而且可以鍛煉學生的邏輯思維能力，同時還能提高學生的數學理解和運算能力，鞏固數學知識學習效果，促使學生在深度掌握數學知識基礎上獲得更多能力的發展。當然，作為一種有效教學工具，運用思維導圖教學還需要教師在實踐中不斷加以研究、完善，使其發揮出最大功效。