相場法研究Fe84Cu15Mn1 合金富Cu 相析出的內磁能作用機理*

蔣新安 趙宇宏 楊文奎 田曉林 侯華

(中北大學材料科學與工程學院,太原 030051)

本文基于連續相場模型,對內磁能作用下Fe-Cu-Mn 合金中富Cu 相析出行為進行了研究,得到不同溫度、不同Mn,Cu 含量條件下的內磁能對富Cu 相的平均顆粒半徑、體積分數、吉布斯自由能的影響.模擬結果表明,Mn 含量越低,居里溫度越高,內磁能對自由能的貢獻越大,且內磁能的貢獻隨溫度升高而減小;內磁能降低了相結構轉變勢壘,促進了相結構轉變.沉淀相體積分數隨Cu 含量增加而增加,通過對比有無內磁能對沉淀相體積分數的影響,內磁能作用導致沉淀相擁有更大的體積分數.因此在內磁能作用下,富Cu 相具有較大的平均粒徑、體積分數和較小的矯頑力,同時預測了合金硬度的變化趨勢.

1 引言

反應堆壓力容器(reactor pressure vessel,RPV)作為核電站的核心設備,其安全使用年限決定了核電站的壽命[1],有研究表明時效或輻射誘導Cu/Mn/Ni 沉淀會導致RPV 鋼硬化造成脆裂[2?4],將嚴重影響核電站的安全使用壽命.一般外界因素如輻照或彈性效應往往掩蓋了磁能對沉淀析出的貢獻[5?9].但是,Gorbatov 等[10,11]研究發現,鐵的磁性狀態在Fe-Cu 合金的分解中起著至關重要的作用,并且為了正確地對Fe-Cu-X 合金中的析出現象進行理論上的描述與分析,應正確考慮磁性及其與溫度有關的貢獻,并從基于密度泛函理論的第一性原理有效對相互作用(effective pair interactions,EPI)統計熱力學模型研究了Fe-Cu-X(X=Ni,Mn)合金體系中的分解,結果表明EPI 表現出對磁性的強烈依賴性,影響不同溫度下的相分離.文獻[12]指出吉布斯自由能(Gibbs free energy,GFE)作為沉淀析出的主要驅動力可以表示為磁性貢獻和非磁性貢獻的疊加.

磁性作為材料的物理性能,實驗手段無法將材料的物理性質脫離材料本體進行單獨研究.但是,以熱力學和動力學為基礎的相場法能夠定量描述固態相變過程中組織及結構、化學、熱力學參數隨時間的演化過程[13?20].因此,采用相場法可以定量的從微觀角度模擬、預測 RPV 鋼中富Cu 相的沉淀演化過程.

Wang 等[21]研究指出,剩磁(remanence)Br和飽和磁感應強度(saturation magnetic induction)Bs的一致變化反映了材料磁化強度的整體變化,磁性的變化往往會導致內部磁場發生變化.內磁能(internal magnetic energy,IME)即內部磁場變化所產生的能量,本工作將IME 耦合到自由能項中,分別研究了不同溫度、不同Mn,Cu 含量條件下的IME 對富Cu 相的平均顆粒半徑、體積分數、吉布斯自由能的影響.本文研究IME 對Fe-Cu-Mn合金富Cu 沉淀過程的演化機理,將對RPV 鋼的合金設計和沉淀相析出機理有重要指導意義.

2 相場模型

對于Fe-Cu(原子含量為15%)-Mn(原子含量為1%)三元合金沉淀演化,引入3 個濃度場ci(r,t)(其中i=1,2,3 分別代表Fe,Cu,Mn)和一個結構序參數η(r,t),這些場的時間以及微觀結構演化是通過Cahn-Hilliard (C-H)方程和Allen-Cahn (A-C)方程[22,23]的數值解獲得:

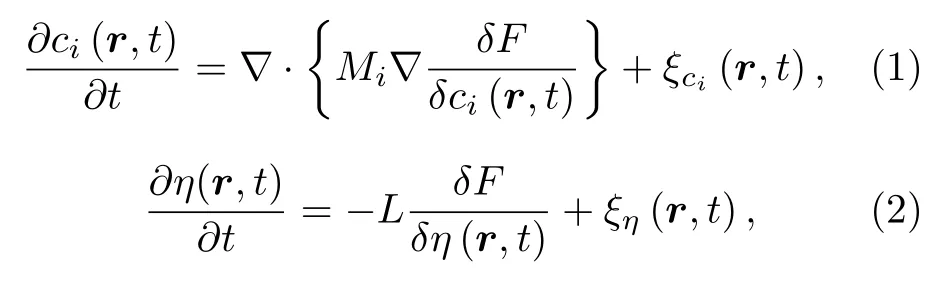
其中,ξc(r,t)和ξη(r,t) 是隨機熱波動項,以促進相分離的發生;Mi(i=Cu,Mn) 是合金成分的化學遷移率;L是表征相變演化的動力學遷移率.Mi與組成元素的原子遷移率有關[24?26]:

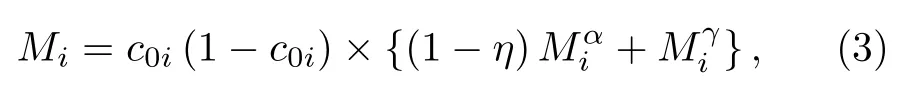
其中,c0i表示合金元素的標稱成分i,分別表示α(BCC)和γ(FCC)相的原子遷移率[27?29]:

其中,R為氣體常數,T為絕對溫度,擴散系數可分為頻率因子和擴散激活能,可以寫為[30,31](具體參數見附錄A)

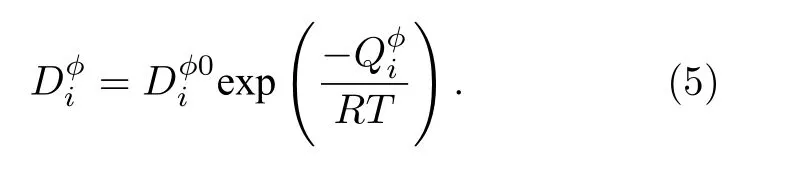
2.1 系統總自由能

為了定量模擬微觀結構變化,需要精確計算微觀結構的總自由能泛函[32],非均勻系統的總自由能F為[33]

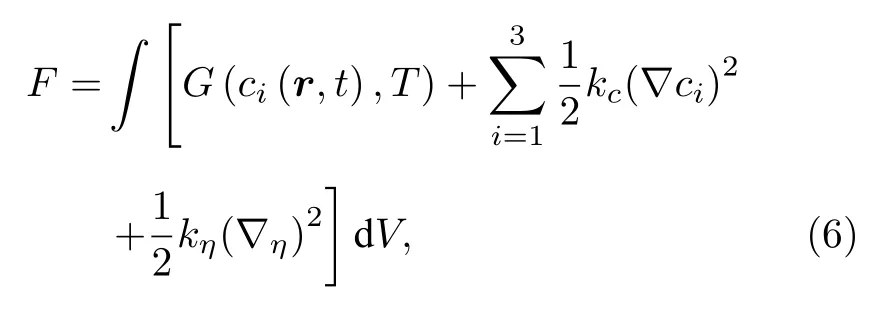
式中,G(ci(r,t),T) 代表系統的體積自由能,ci(r,t)表示在空間位置r和時間t下成分i的局部成分場,兩項中kc和kη分別為成分梯度能系數以及序參數梯度能系數.

系統的體積自由能可以表示為

其中,函數h(η) 被定義為h(η)=η2(3?2η)[34,35],是0—1 之間的單調函數;Gα(ci,T)和Gγ(ci,T) 為ci和T的函數分別表示α相和γ相的吉布斯自由能;Wg2(η)表示BCC 相和FCC 相之間的相變能壘,W是雙勢阱的高度,通常取一個很大的正數,g(η)=η(1?η).

用亞正則溶液近似描述了Fe-Cu-Mn 三元合金體系中相的化學自由能[36],本模擬所使用的吉布斯自由能函數G?(ci,T)(?=α,γ) 為

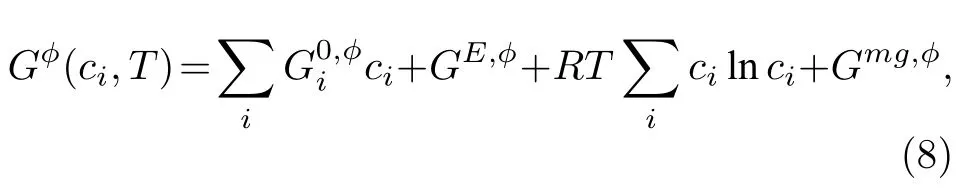
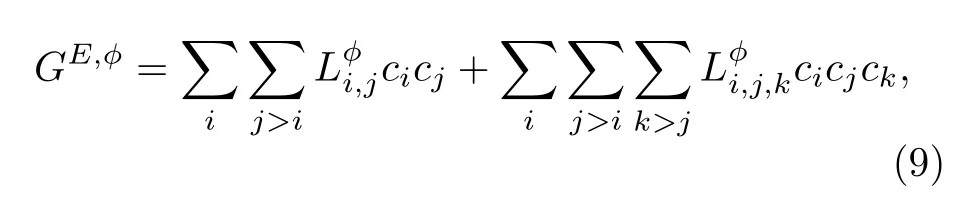
由(3)式可知,吉布斯自由能包括以下幾項:純元素的GFE、混合GFE、過剩GFE 和磁能.當前,大部分研究在用相場法計算合金的自由能時,為了簡化處理都不考慮IME 的影響[6,7,38?40].但是IME 對合金中析出相也會有影響,尤其對于含有鐵磁性元素Fe,Mn 的合金非常有必要研究.

Gmg,?是內磁能對GFE 的貢獻,可以表示為

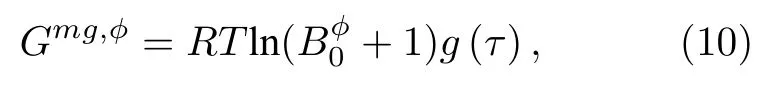
3 模擬結果與分析

在給定的熱力學條件下,亞穩相將轉化為具有最小吉布斯自由能的穩定相[41],圖1 所示為不同溫度條件下,有無IME 作用GFE 隨Cu 含量的變化情況.可以發現,無論有無IME 作用的影響,GFE 隨Cu 含量增大都會呈現出先升高再降低的變化趨勢,文獻[42] 指出Cu 顆粒的沉淀過程可以看作偽失穩分解,富Cu 析出相除了早期Cu 元素的積累外,還經歷了BCC-FCC 的相結構轉變,符合偽失穩分解的特征:1) 物質的一種或多種組分通過擴散過程重新分布,形成富集區和枯竭區;2)富集或枯竭區域發生結構轉變,產生與母相(即基質)不同的晶格結構的新相.如圖1(a)所示,不考慮IME 作用影響時,無論溫度高低,FCC 結構相的GFE 總是低于BCC 結構相,說明此時的沉淀相總是具有最小GFE 的穩定FCC 相,這與相圖結果不符[43,44].因此,又考慮了IME 對雙相GFE 的影響,如圖1(b)所示.在IME 作用影響下兩相自由能存在交點,當Cu 含量分別小于0.72,0.69,0.62,0.49 時,BCC 固溶體GFE 要明顯小于FCC 固溶體,并且BCC 相結構要比FCC 更穩定;當Cu含量分別大于上述濃度值時,FCC 結構相能量要小于BCC,這說明在此實驗溫度條件下,隨著Cu 濃度升高,BCC 結構逐漸向FCC 結構發生轉變;同時由高溫到低溫對比了4 組不同溫度條件下的曲線,臨界點有明顯左移現象,說明相結構轉變對溫度的變化存在依賴性.在溫度為823 K 時,FCC 向BCC 轉變的Cu 含量臨界值為0.69,從理論上講,當體系某點的Cu 濃度超過0.69 時就已經發生了由BCC 向FCC 的轉變,與偽失穩分解的特征相吻合,并且隨著Cu 含量的增加,FCC 結構的能量會更低,形成穩定的FCC 沉淀相,這種現象在文獻[45]中也被證實過.由此可見,IME 對體系自由能和相結構轉變的貢獻不可忽略.

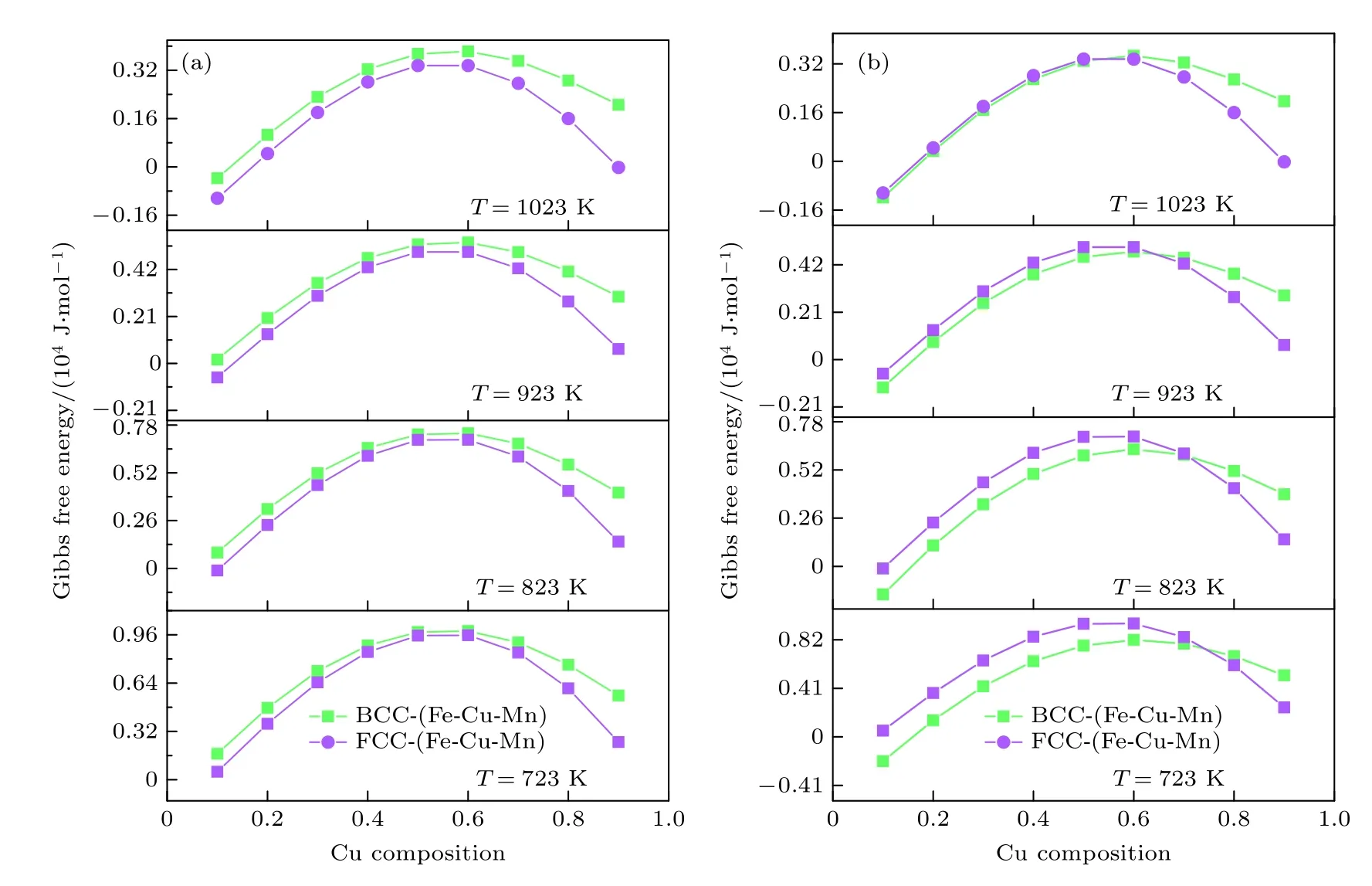
圖1 不同溫度下GFE 隨Cu 濃度變化情況 (a) 不考慮IME 作用;(b) 考慮IME 作用Fig.1.Gibbs free energy versus Cu concentration at different temperatures:(a) The effect of internal magnetic energy is not considered;(b) the effect of internal magnetic energy is considered.

IME 不僅影響相結構轉變的GFE,還對沉淀相長大階段形貌有影響.圖2(a)—(f),(j),(k)分別為無IME、有IME 作用下的沉淀演化過程以及晶粒尺寸對應不同時間步數的曲線.時效初期(t?<7500),Cu 原子隨機分布在Fe 基體中,隨著演化的進行,溶質的過飽和為成核和結晶提供了化學驅動力,Cu 原子聚集形核,并以吸收基體中Cu 原子的方式不斷析出.富Cu 相不斷長大并達到穩定的晶粒尺寸.如圖2 所示,相同時間步數下,無IME 作用下的成分起伏點更多,并且優先析出沉淀相(如圖2(b)紅色標注).當析出相長大到一定尺寸時,有IME 作用下才出現個別沉淀相(如圖2(c),(h)黃色標注).當無IME 作用下的沉淀相數量和尺寸趨于穩定時,有IME 下的沉淀相還處于長大階段.對比可以發現IME 對沉淀相的形核演化過程有一定的阻礙作用.圖2(k)為演化過程中的顆粒半徑變化圖,其中No-IME 表示沒有IME 作用,With-INE 表示有IME 作用,斜率大小代表了尺寸變化率的大小.對比兩個狀態下的平均顆粒半徑,IME作用下的平均半徑大于無磁能作用下的平均顆粒尺寸.并且在長大階段,無IME 狀態下尺寸變化率更高.當沉淀相的平均半徑達到2.69 nm 時,尺寸變化率又趨于平緩,有IME 作用下的平均顆粒半徑以穩定的變化率呈線性增長,達到穩定時尺寸將不再變化.說明IME 對顆粒的長大過程和顆粒尺寸也有較大的影響,并且在IME 的影響下顆粒長大過程更加平穩.

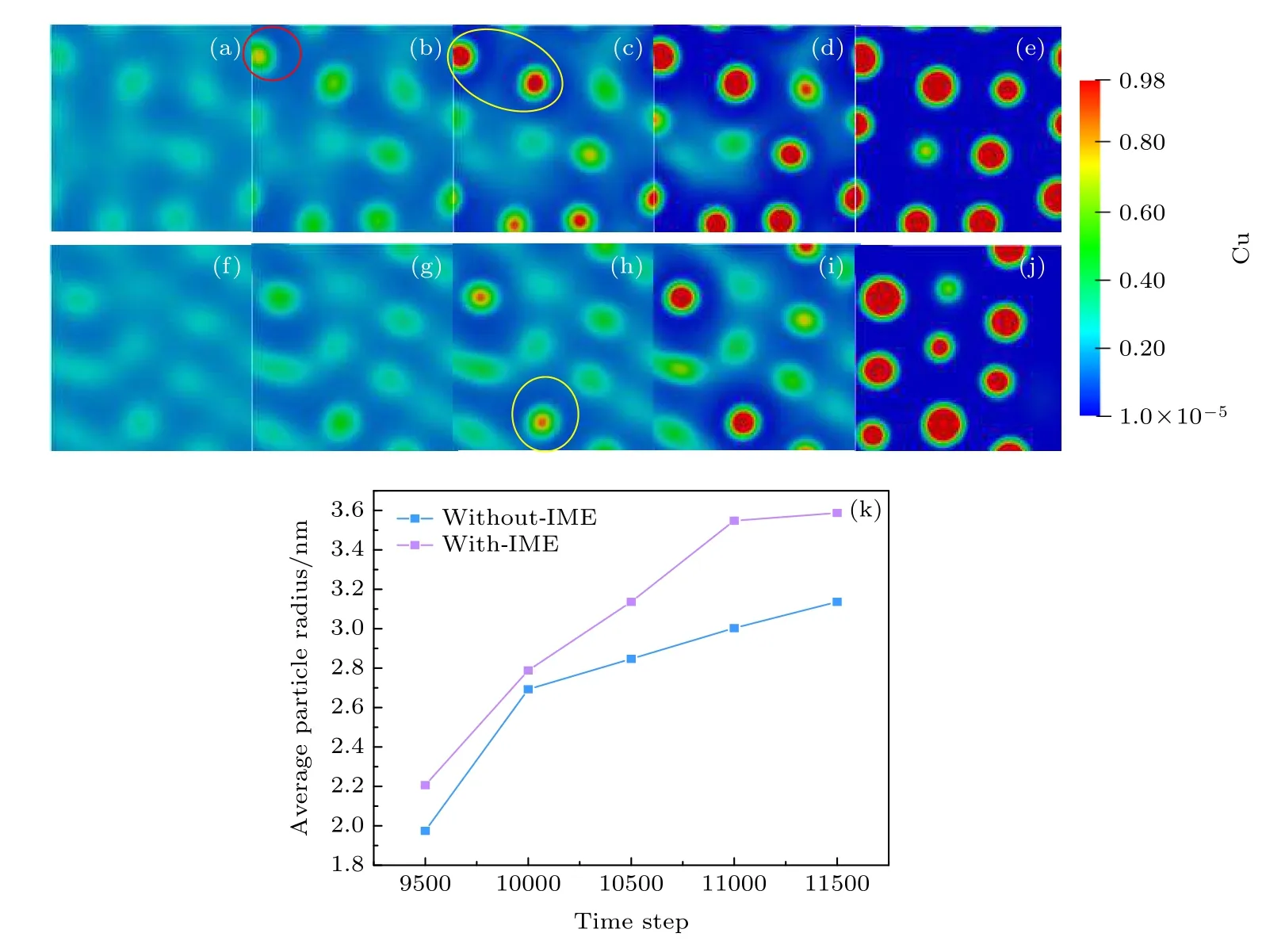
圖2 (a)—(e) 823 K 時無IME 作用下的演化過程 (a) t?=7500,(b) t?=8500,(c) t?=9000,(d) t?=9500,(e) t?=11000;(f)—(j) 有IME 作用下的演化過程 (f) t?=7500,(g) t?=8500,(h) t?=9000,(i) t?=9500,(j) t?=11000;(k) 有IME 與 無IME 作用下的平均顆粒半徑變化Fig.2.(a)–(e) The evolution process without internal magnetism at 823 K:(a) t?=7500,(b) t?=8500,(c) t?=9000,(d) t?=9500,(e) t?=11000;(f)–(j) the evolution process with internal magnetism:(f) t?=7500,(g) t?=8500,(h) t?=9000,(i) t?=9500,(j) t?=11000;(k) the change of average particle radius with and without internal magnetism.

合金元素取代Fe 原子會導致局部磁態以及晶體結構的轉變[46],而作為順磁性元素Mn 還會加速沉淀動力學[11,47,48].由于Cu 在Fe 中的溶解度不高,并在Fe 基體中快速擴散[49],因此最初富含Cu 的沉淀相,通常與Mn 形成合金.并且最初Mn偏析導致界面能的降低,因此會迅速形成高密度的富銅析出相[50].如圖3(a)所示,演化初期,Cu 和Mn 元素在相同的位置出現了成分起伏,磁化強烈影響最鄰近原子的相互作用,特別是在Mn-Mn 和Cu-Cu 對的情況下,它們表現出不同的有序趨勢.雖然Mn 原子在鐵磁性(ferromagnetic,FM)狀態下相互排斥,但Cu 原子之間卻相互強烈吸引,且Mn 對Cu 原子也有強烈的吸引力,這是Cu 原子在原子團簇中的原因[11,51].Mn 和Cu 相互作用處的濃度略高于基體中濃度,并且此處的濃度不斷增大,但不同的是,Cu 的濃度從最初的成分起伏一直聚集,核心Cu 的濃度遠高于基體中Cu 的濃度,最終達到了99%,如圖3(b)所示.

觀察Mn 的成分曲線可以發現,Mn 元素先出現了成分起伏,核心處Mn 的濃度略高于基體其他區域,濃度達到最大值時,曲線頂點有凹陷趨勢,說明在演化過程中,Mn 則從核心不斷被“排擠”到核心周圍形成環形富集區,如圖3(c)所示.Cu 位于沉淀相的中心,而Mn 則偏析在沉淀相與基體之間的界面形成殼層結構,上述過程如圖4(a)—(c)所示,最終形成以富Cu 相為核心,Mn 元素在外層形成環狀的元素分布,如圖4(d)所示,這種富Cu 沉淀相具有核-殼結構的現象也在文獻[8,11,52?54]中被證實,這也與偽失穩分解特征相吻合,并且隨著Cu 的富集長大,Mn 環尺寸隨之變化,如圖3(d)所示.

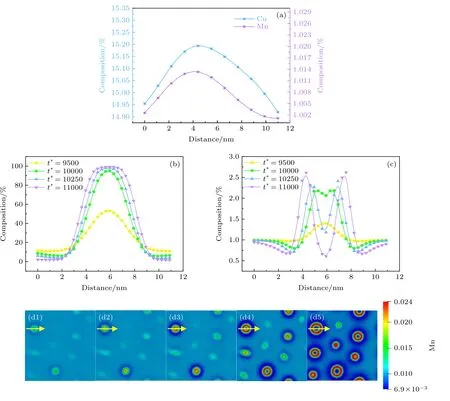
圖3 溫度為823 K 時IME 作用下Mn 與Cu 沉淀析出的成分曲線(原子含量) (a) 早期(t *=2500)時Cu 與Mn 的成分曲線;(b) 不同時間步數Cu 的成分曲線;(c) 不同時間步數Mn 的成分曲線;(d) Mn 環在不同時間步數的演化過程Fig.3.The composition curve of precipitation of Mn and Cu under the action of magnetic energy in 823 K (atomic percent):(a) The composition curve of Cu and Mn in early (t *=2500);(b) composition curve of Cu with different time steps;(c) composition curve with different time step size of Mn;(d) evolution process of Mn ring with different time steps.

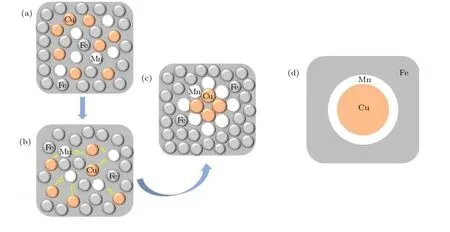
圖4 Cu 原子和Mn 原子相互作用和局部元素分布示意圖 (a)—(c) Cu,Mn 原子相互作用示意圖;(d) Fe,Cu,Mn 局部元素分布示意圖Fig.4.Schematic diagram of Cu atom and Mn atom interaction and local element distribution:(a)–(c) Schematic diagrams of Cu and Mn atom interaction;(d) schematic diagram of local element distribution of Fe,Cu and Mn.

4 討論

4.1 影響IME 的因素

為什么圖1(b)中α相與γ相的GFE 差值隨溫度升高而減小? IME 是如何作用于總GFE? 圖5(a)是α相和γ相居里溫度與Mn 含量的關系,根據(10)式和(11)式所得,α相的居里溫度隨Mn 含量升高而降低,且Mn含量為0.01 時的居里溫度為1027 K,高于實驗溫度.圖5(b)為α相和γ相的內磁能隨溫度以及Mn 含量的變化,可以發現α相的內磁能隨溫度升高而逐漸趨于0,且初始值隨Mn含量升高而降低.根據圖5(a)所示,Mn 含量降低了居里點,當溫度接近并超過居里點時內磁能將逐漸減小且由鐵磁性向順磁性發生轉變[55],故內磁能逐漸趨于0,對總自由能的貢獻也隨之減小.而γ相的居里溫度變化趨勢則與α相相反.在該實驗溫度條件下(Mn 含量0.01—0.03 區間,實驗溫度723—1123 K)遠高于γ相的居里點,故γ的內磁能均近似于0,對總自由能的貢獻可以忽略不計,這也解釋了圖1(b)中α相和γ相自由能在初始值的差值隨溫度不斷增大而減小.結合圖5(b)和圖5(c)發現,隨著Mn 含量升高,總自由能的最高值反而降低,說明在演化后期IME 對總GFE 的影響遠低于純組元GFE 的貢獻.綜上所述,IME 對成核階段的影響作用最大,隨著演化的進行,作用效果逐漸減小.

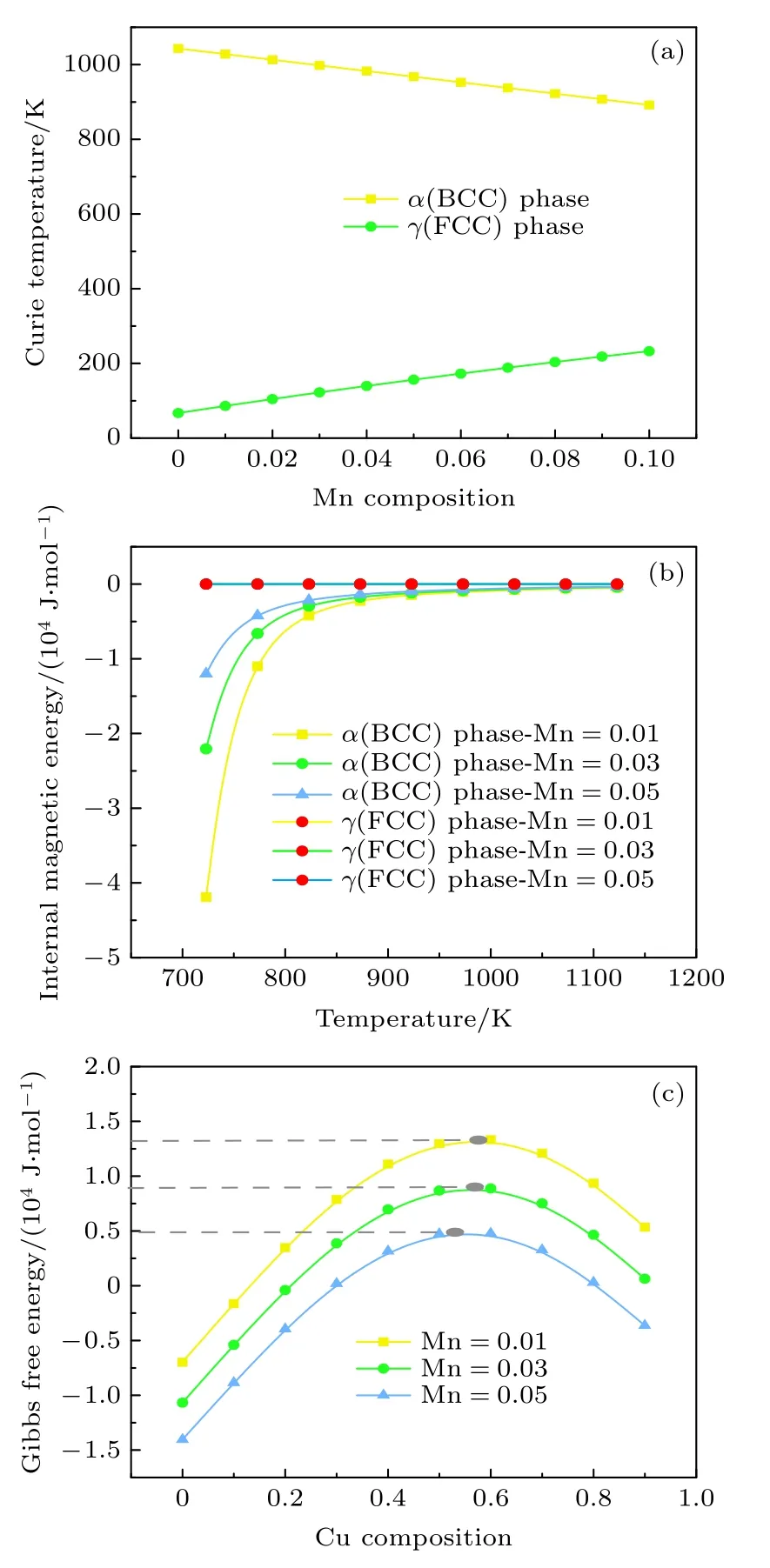
圖5 溫度為823 K (a) Mn 含量與居里溫度的關系;(b) 溫度與IME 的關系;(c) 不同Mn 含量下吉布斯自由能Fig.5.At 823 K (a) Relationship between Mn content and Curie temperature;(b) relationship between temperature and internal magnetic energy;(c) Gibbs free energy with different Mn content.

4.2 IME 影響沉淀相形貌的原因

研究表明,決定合金元素間相互作用特性的重要因素是基體的磁性狀態[46,56].為了減少鐵磁性元素含量對結果的影響,選取了非鐵磁性元素Cu 含量為變量.如圖6 所示,體積分數隨Cu 含量的增大而增大,但值得注意的是,無論Cu 含量為多少,在IME 作用的影響下,總擁有更高的體積分數.并且在Cu 含量為0.15—0.35 范圍內,有IME 作用下的體積分數均大于無IME 作用.因為磁性對Mn 的溶解過程都有重要的作用[46],Mn 在FM 狀態下對Cu 原子也表現出明顯的吸引力[11],如圖3(a)所示,并且在演化過程中Cu 會在Cu-Mn 沉淀相的核心長大,而Mn 則偏析在沉淀相與基體之間,降低了沉淀相與基體相之間的界面能,減少了Cu 遷移的阻礙,進一步促進富Cu 相的析出[57].Mn 原子作為非常穩定的混合啞鈴溶質[58],混合啞鈴旋轉不需要太多能量,因此Mn 溶質通過平移和旋轉的機制進行遷移并進行團簇,而這些團簇又成為其他啞鈴的缺陷[57],Mn 不斷以這種機制在界面處富集,從而影響富Cu 沉淀相的演化過程.Mn在低含量時(<0.05)低溫時IME 對總自由能的貢獻最大,也就是說在演化早期的長大階段,IME 對體系的貢獻最大,影響了后期粗化階段,故在IME作用下擁有更大的體積分數,也說明IME 對沉淀相的體積分數也有積極作用.故IME 對體系的體積分數的貢獻也是不可忽視的.

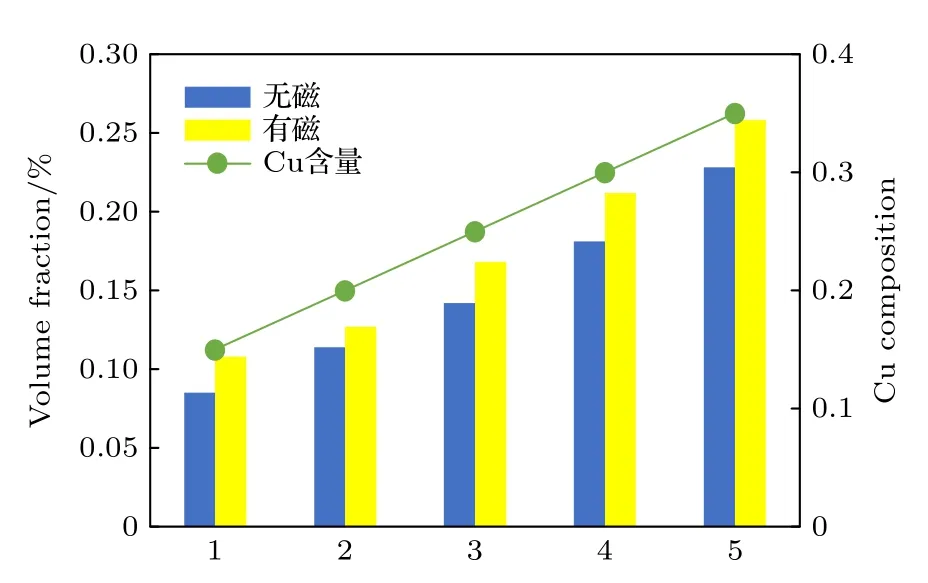
圖6 在有無IME 作用下體積分數隨Cu 含量的變化Fig.6.Variation of volume fraction with Cu content with or without internal magnetic energy.

4.3 IME 對材料硬度的影響

文獻[21]研究發現,與拉伸性能相比,硬度和磁性對RPV 鋼的時效變化更為敏感,然而相結構的轉變會給磁疇壁的移動帶來額外的障礙[59],從而影響合金的IME,這種障礙也會隨著沉淀相的增大而導致矯頑力達到最大值[60?62],富Cu 相會成為疇壁位移的障礙,并且在富Cu 相附近,磁矩會向磁晶各向異性的方向偏轉,這種偏轉疇壁的位移是富Cu 相導致矯頑力(coercivity)Hc增大的主要機制[63].根據上文,IME 會影響富Cu 相的析出,而由于富Cu 相的析出,基體中組成也發生了變化,從而導致Bs的變化,可見IME 通過影響富Cu 的析出而影響整個體系的磁性狀態.其中,矯頑力Hc與平均顆粒尺寸D的關系為[64]

其中,C為材料有關的常數(居里常數),D為沉淀相顆粒的平均半徑.值得注意的是,如圖7(b)所示矯頑力與硬度近似線性的關系,可以估計材料硬度變化[21].相場模擬發現,在IME 作用下富Cu 相具有更大的平均顆粒半徑,如圖2 所示.根據(17)式,Hc與D的關系如圖7(a)所示,相同實驗條件下,考慮C為常數,D1Hc2,由此可得,具有較小平均顆粒半徑的富Cu 沉淀相,擁有更大的矯頑力,又如圖7(b)所示,硬度值隨矯頑力而增大.因此IME 作用下Fe-Cu-Mn 合金的硬度值更小.

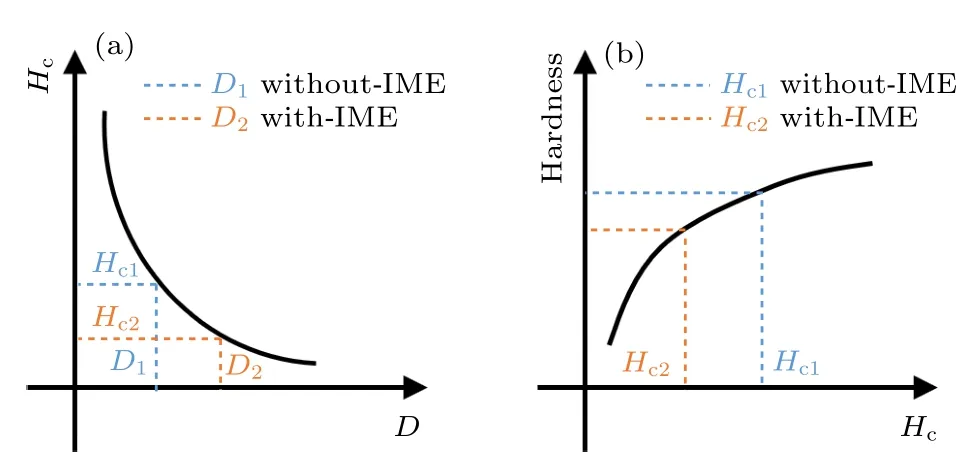
圖7 矯頑力(Hc)與顆粒半徑以及硬度的關系示意圖(a) Hc 與平均顆粒半徑的關系示意圖;(b) Hc 與硬度關系示意圖Fig.7.The relationship between coercivity (Hc) and particle radius and hardness:(a) Schematic diagram of relationship between Hc and average particle radius;(b) schematic diagram of relationship between Hc and hardness.

5 結論

IME 可降低相結構轉變勢壘,使得相結構轉變所需要的能量較低,相較于無IME 作用下的Fe-Cu-Mn 合金更容易發生相結構轉變.

Mn 含量與α相的居里溫度呈反比,當Mn 含量從0.01 增至0.05 時,該合金α相居里溫度從1027 K 降為967 K.在相同的居里溫度下,IME 對總自由能的貢獻隨實驗溫度升高而減小.

在IME 作用下,富Cu 沉淀相擁有更大的平均顆粒半徑以及平衡態時的體積分數和較小的矯頑力,根據矯頑力與硬度的線性關系,IME 作用下Fe-Cu-Mn 合金的硬度值更小

附錄A

純組元i吉布斯自由能和二元和三元的相互作用參數相關參數來源于文獻[65,66].對于Fe-Cu-Mn三元合金體系而言,有3 個二元系Fe-Cu,Fe-Mn,Cu-Mn和1 個三元系Fe-Cu-Mn.因此二元和三元系的相互作用參數具體值為[37,65,66]: