含記憶阻尼函數的周期勢系統隨機共振*

許鵬飛 公徐路 李毅偉 靳艷飛

1) (山西農業大學數學系,太谷 030801)

2) (山西農業大學軟件學院,太谷 030801)

3) (北京理工大學力學系,北京 100081)

研究了外部周期信號和內部噪聲共同激勵下,含記憶阻尼函數的周期勢系統的隨機共振.針對具有多穩態特征的周期勢系統,推導出適用于一般多穩態模型的系統響應振幅和功率譜放大因子.研究結果表明,功率譜放大因子隨溫度的變化曲線出現單峰,說明含記憶阻尼函數的周期勢系統存在隨機共振現象,并且系統的記憶特性和穩態點數量對共振行為有著顯著影響.此外,利用隨機能量法進一步分析了系統的隨機共振現象,發現共振效應隨著記憶時間的增加先減弱再增強.在適當的溫度條件下,存在最優記憶時間可以最大化外部周期力對系統所做的功.

1 引言

隨機共振的概念由Benzi 等[1]在研究古氣象冰川期問題時提出,其理論發展及應用已經在不同科學系統中取得顯著成果[2?4],但較少涉及含記憶阻尼的動力系統.該系統描述了一類處于無序介質或復雜環境下的non-Markovian 過程[5?8],例如處于生物細胞、湍流、生長表面、滲透媒介、黏性材料等背景中的粒子就展示出偏離Brown 運動的反常擴散行為,它的運動速度所產生的記憶效應歸因于空間和時間上的非局域特性.針對這類含記憶效應的隨機系統,廣義Langevin 方程(generalized Langevin equation,GLE)是研究其動力學行為的主要手段之一[9?14].特別地,GLE 中的阻尼項取決于隨時間變化的記憶核函數,其中記憶核的類型主要包括了冪函數型[9]、不同形式的指數函數型[10?12]以及Dirac delta 函數與指數函數的混合型[13,14]等.在隨機模型中,外部噪聲主要源于系統所處的環境或實驗內的噪聲發生器,而GLE 中的內部噪聲通過漲落耗散關系依賴于系統的記憶阻尼核函數[15],即內部噪聲和耗散產生于同一隨機源,從而使系統處于平衡狀態.在GLE 刻畫的動力模型中,噪聲誘導行為以及記憶性對動力學現象的影響已經在不同學科領域內受到研究者們的關注,例如反常擴散[9?11]、信息熵[16]、平均首次穿越時間[17]、隨機共振[18?22]等.其中,在含不同記憶阻尼函數的線性系統中,文獻[18?20]基于GLE分別詳細討論了時滯、固有頻率漲落噪聲及Mittag-Leffler 噪聲作用下的隨機共振現象.在攜有指數型記憶核的雙穩態系統中,Hasegawa[21]和Srokowski[22]均通過GLE計算了系統的功率譜放大因子,并分析了不同條件下記憶效應對隨機共振的影響.在非對稱三穩態系統中,研究表明記憶時間抑制相干共振,卻增強隨機共振[13].由于廣義Langevin 系統存在著顯著的non-Markovian 性質,故導致它的動力學特性復雜多變,分析困難.然而,在GLE 描述的周期勢系統中,尚未出現關于隨機共振現象的研究,尤其記憶效應對共振行為的影響.

另一方面,具有多穩態特征的周期勢模型已在物理、化學、生物、工程等領域內展示出了廣泛的應用,如Josephson 隧道結[23]和分子馬達[24]等.周期勢系統中噪聲誘導動力學的研究也呈現出豐碩的成果,例如:噪聲誘導的粒子輸運[25]、棘輪效應[26]、穩定性[27]、相干共振[28]等.此外,Saikia[29]在二階欠阻尼的周期勢動力系統中引入隨機能量法作為衡量隨機共振的特征指標,發現隨機共振出現在驅動信號的高頻區域內,且兩個動力學狀態的穩定性與隨機共振效應依賴于系統的阻尼參數和信號幅值.Reenbohn 等[30]研究了欠阻尼傾斜周期勢中的隨機共振,并基于兩個具有不同振幅和相位的動力學狀態解釋了共振行為的發生.Nicolis[3]將隨機共振理論拓展至過阻尼多穩態模型中,解釋了系統在初始狀態與最終狀態的躍遷過程中可以同時存在任意數量的中間穩定狀態,發現適當數量的穩定狀態可使周期勢系統響應最大化.在高斯白噪聲和輸入信號共同作用的周期勢模型中,通過矩方法[31]和仿真實驗[32]詳細分析了隨機共振現象.周期勢系統的隨機共振還在多種形式的噪聲激勵下得到研究,例如多值噪聲[28]、Lévy 噪聲[33]、高斯色噪聲[34]等.但上述研究都是依據經典的Langevin方程進行,且多穩態特征導致理論分析尤其缺乏,主要局限在數值和實驗方面的研究.

本文研究了外部周期信號驅動下含記憶阻尼函數的周期勢系統的隨機共振.首先介紹了GLE描述的含記憶阻尼函數的二階動力學模型.然后,在多穩態情形下,率先推導了系統功率譜放大因子的解析表達式,并進一步計算了系統的輸入能量.最后,從這兩個角度研究了周期勢模型的隨機共振現象,詳細分析了記憶效應和多穩態特征對共振行為影響.

2 系 統

本文考慮的模型描述了單位質量的粒子在周期勢U(x) 中的運動,其中系統含有依賴于時間變化的記憶阻尼函數,且受到內部噪聲和外部周期信號的共同作用.該數學模型通過廣義Langevin 方程表示為如下形式[11]:

其中x(t) 代表粒子運動的位移;參數ε0和ω分別表示外部周期信號的振幅和頻率.特別地,內部噪聲ζ(t)的均值為零,其自相關函數與系統的記憶阻尼核γ(t) 之間滿足漲落耗散理論[15],即

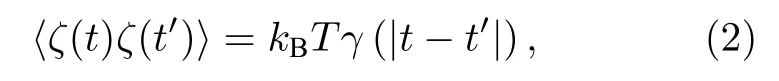
這里kB是Boltzmann 常數,T是環境的絕對溫度.記憶核函數γ(t) 是由一個Dirac delta 函數和一個含記憶時間τc的指數型函數構成[13,14]:

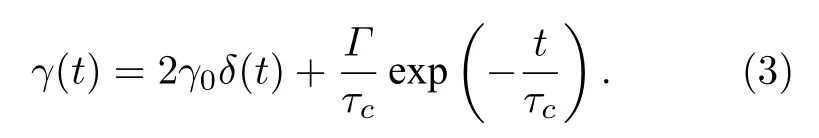
從記憶核函數方程(3)中容易發現方程(2)中的內部噪聲ζ(t) 可看作兩個相互獨立的噪聲項之和,即Delta 關聯的高斯白噪聲和指數關聯的色噪聲.因此,系統(1)式具有短時間的Markovian 特征和相對長時間的non-Markovian 特征,其中記憶效應由方程(3)中隨時間演化而指數衰減的函數項來刻畫,這里參數Γ代表系統的記憶強度.含此類記憶核的廣義Langevin 方程廣泛應用于研究復雜環境下非線性系統的物理現象,典型案例包括在具有均勻靜磁場的平面上,受雙諧方式約束的帶電粒子的軌道磁矩[11];過阻尼雙穩態模型中的隨機共振現象[35];帶電粒子在黑體輻射中的彈道擴散行為[36].當記憶性不存在時(Γ=0),系統(1)式退化成了一個傳統的高斯白噪聲激勵的二階動力系統模型.

針對系統(1)式引入新變量y(t) 和z(t) 進行變換,則原系統等價地描述為具有Markovian 特性的Langevin 方程組:

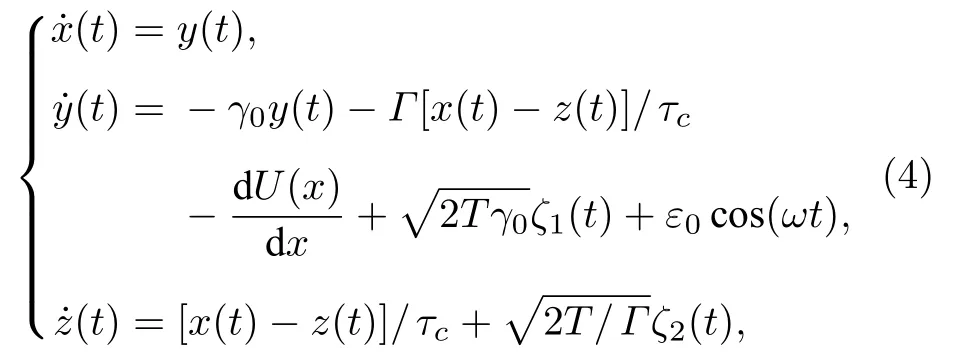
其中噪聲項ζ1(t)和ζ2(t) 是兩個無關聯的高斯白噪聲,滿足統計性質:〈ζi(t)〉=0,〈ζi(t)ζj(t′)〉=δi,j(t ?t′)(i,j=1,2).特別地,方程組(4)中的新變量z(t) 具有如下形式:

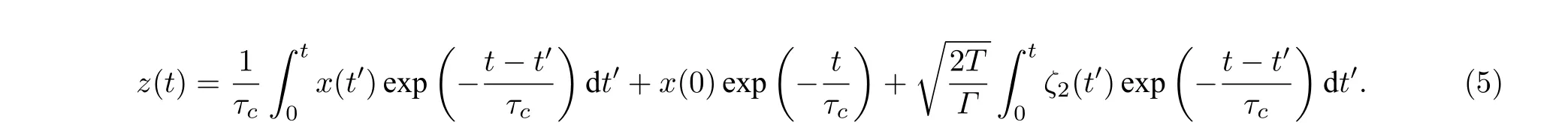
令ρ(x,y,z,t) 表示方程(1)在t時刻處于狀態 (x,y,z) 的概率密度函數,則獲得其滿足的Fokker-Planck 方程:

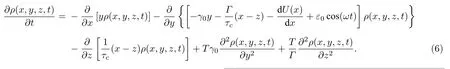
對于(6)式中不含外部周期信號的情形(ε0=0),在細致平衡條件下,獲得平穩概率密度函數ρst(x,y,z)的解析表達式:

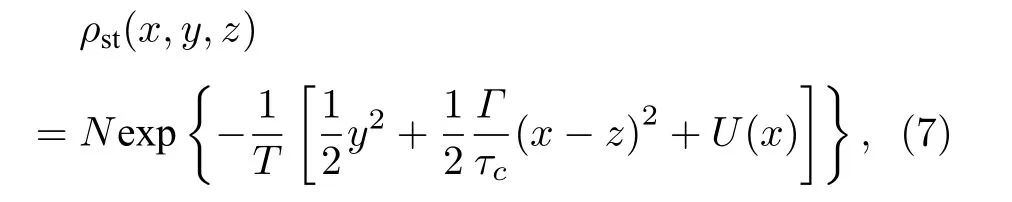
其中N表示全概率歸一化的常數.

當系統(1)式受外部周期信號ε0cos(ωt) 作用時,假定其振幅ε0充分小以致能夠進行小參數展開計算,且信號為閾下激勵.同時,限制頻率ω ?1,使得系統在一個信號周期內有足夠長的時間達到局域平衡態,即滿足絕熱驅動.從而可獲得Fokker-Planck 方程(6)的準穩態解[37],其中廣義勢函數結合方程(7)整理為如下形式:

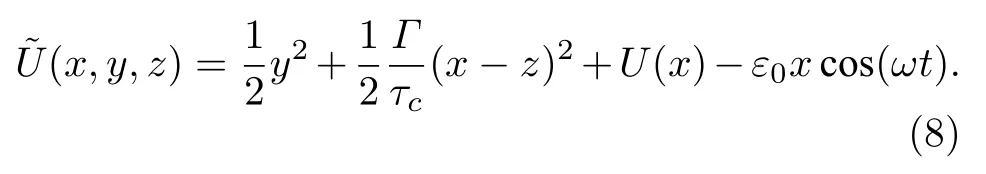
本文考慮系統(1)為周期勢系統,即勢函數U(x)=?cos(m0x),從而確定性系統(4)存在多個穩定平衡點sn(xsn,0,xsn) 和不穩定平衡點是un(xun,0,xun),其中xsn=2nπ/m0,xun=(2n+1)π/m0,m0和n均為正整數.如圖1(a)所示,隨著m0的變化,勢阱的寬度發生變化,設置m0的值可改變給定位移區間內穩態點的個數.圖1(b)給出了離散狀態下該周期勢系統在n個穩定狀態之間躍遷的示意圖.可見,周期勢系統在兩端狀態之間的噪聲誘導躍遷過程中同時存在多個中間穩定狀態,有必要進一步研究穩態點數量、溫度及記憶效應對系統輸出響應的影響.

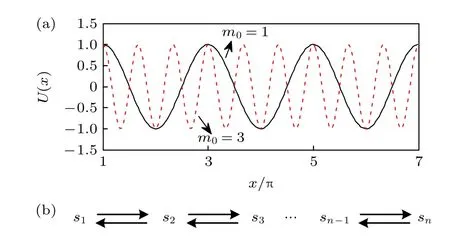
圖1 (a)周期勢函數;(b)離散的多穩態過程Fig.1.(a) Periodic potential;(b) discrete multi-stable process.

3 隨機共振

本節首先依據線性響應理論推導系統關于外部周期信號的響應振幅及功率譜放大因子的解析表達式;再利用隨機能量法進一步計算系統的輸入能量;然后,從這兩個方面分別驗證周期勢模型(1)式中隨機共振現象的產生,詳細討論記憶效應、溫度及系統的多穩態特征對共振行為的影響.

3.1 功率譜放大因子

在絕熱近似條件下[2],系統在每個穩定狀態的吸引域內達到局域平衡所需的時間遠小于系統在不同吸引域之間整體平衡需要的時間,即單個穩態點處的局域平衡時間可以忽略,故連續系統(4)式可近似轉化為一類離散的多穩態Markov 過程.如圖1(b)所示,系統在穩定狀態si處的吸引域內的概率φi可通過方程(6)中的概率密度函數表示為

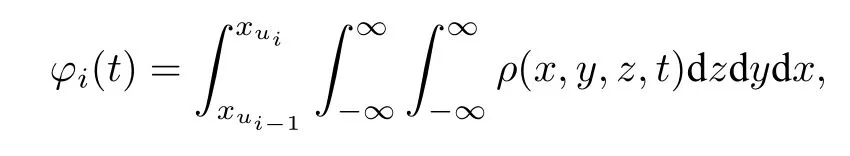
其滿足概率交換的主方程:

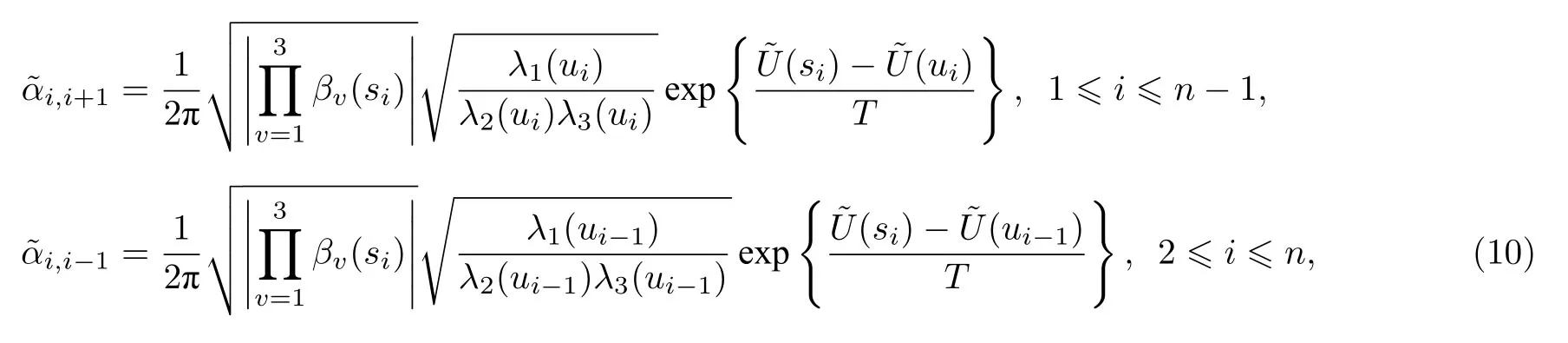
其中βv(si) 表示無噪聲和信號激勵的方程(4)在穩態狀態si(2iπ/m0,0,2iπ/m0) 處的線性化矩陣的特征值;λ1(ui)和λj(ui) (j=2,3) 分別表示無噪聲和信號激勵的方程(4)在不穩定狀態ui((2i+1)π/m0,0,(2i+1)π/m0)處的線性化矩陣的正特征值和負特征值.

根據線性響應理論[39],在長時間極限下,方程(9)的穩態解可分解為如下形式:

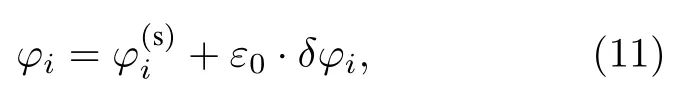
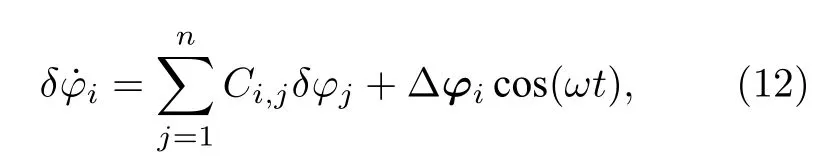
矩陣C和 ?φ分別滿足下列形式:

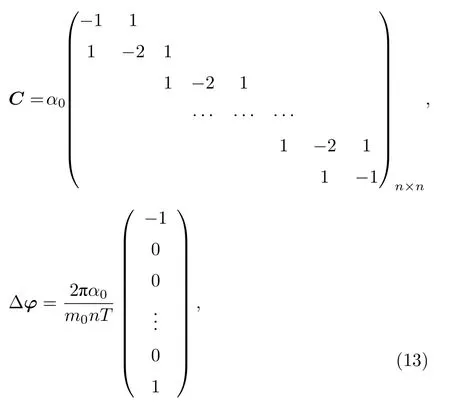
其中α0為方程(9)中無外部周期信號(ε0=0)的概率躍遷速率.

方程(11)中的解δφi可以表示為如下形式:

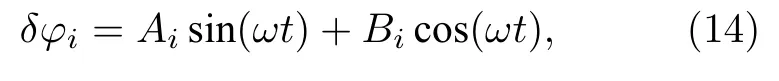
其中Ai和Bi決定了系統關于外部周期信號的響應振幅和相位.替換方程(14)進入方程(12),再比較方程兩邊正弦函數和余弦函數的系數得到Ai和Bi的表達式,從而獲得系統關于外部周期信號的響應振幅ri=即

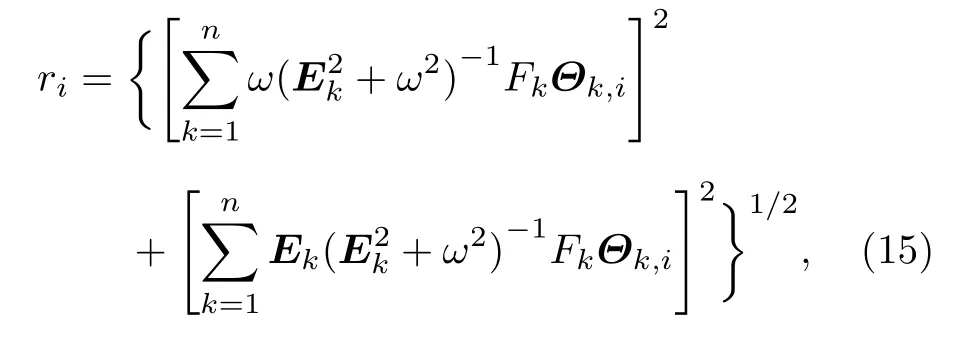
其中Ek和Θk分別表示方程(13)中矩陣C的特征值和特征向量,Fk是方程(13)中矩陣 ?φ在特征向量Θk的展開系數,即具體地,

當系統在穩定狀態時,根據方程(11)表示出依賴時間變化的位移一階矩:

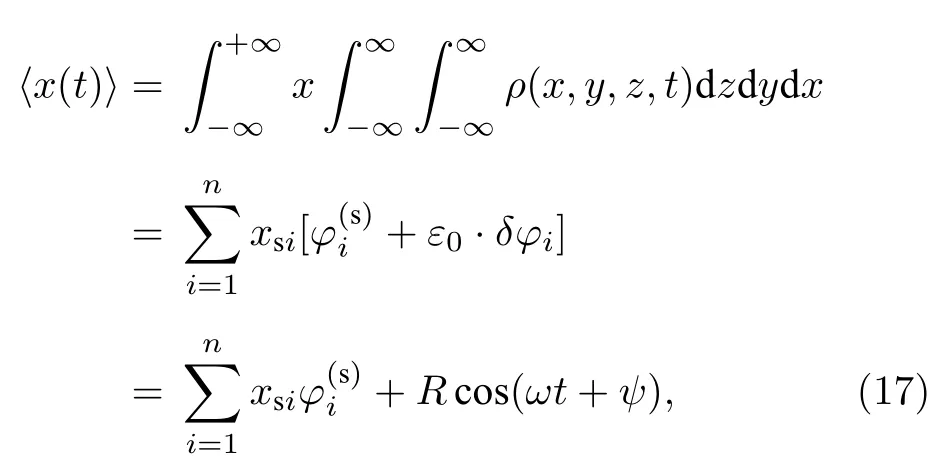
其中R和ψ分別對應系統位移的振幅和相位.進一步,根據方程(15)—方程(17)得到系統功率譜放大因子的解析表達式:

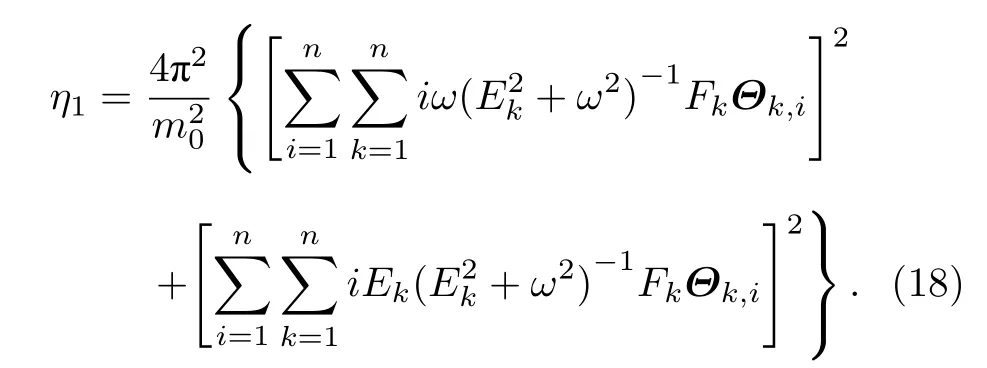
功率譜放大因子(18)式適用于一般的周期勢模型,其依賴于周期勢中連續平衡點的個數,與位置無關.在真實環境中,受噪聲和信號激勵的多穩態系統,其運動軌跡通常局限在一定的范圍內,如圖1(b)所示的多穩態模型.為分析多穩態特征及固定區間內穩態點數量對隨機共振的影響,本節主要考慮周期勢系統(1)式的有限穩態點情形.

根據方程(15)和方程(18),圖2 展示了記憶時間τc對周期勢模型的功率譜放大因子η1和響應振幅ri的影響.在圖2(a)中,η1隨溫度T的變化出現了顯著的共振峰,標志著隨機共振現象的發生.隨著τc的增大,η1的峰值逐漸升高,共振效應增強,且共振峰位置向T減小的方向移動,即噪聲表現出對系統響應的建設性角色得到增強.因此,在周期勢系統(1)中,記憶時間對關于外部周期信號的輸出響應具有積極的增強作用,而相反的情形發生在含記憶阻尼的雙穩態系統中[35],其中記憶性抑制了隨機共振.該現象可通過圖2(b)得到解釋,對于固定的穩態點個數n=30 和不同的τc值,繪制了各個穩態點對應響應振幅ri的變化曲線.在兩個邊界的穩定狀態處(s1和sn),響應振幅得到最大化,并且朝向中間的穩定狀態對稱性減弱,最終達到最小值.這是由于處于中間狀態的系統會等可能地躍遷到兩個相鄰的穩態點處,而在邊界的穩態點處躍遷是不對稱的.另外,各個穩態點的響應振幅均隨著τc的增加而增大,即在適當的記憶時間作用下,外部的弱周期信號在該周期勢系統中得到進一步放大.系統的記憶性是在復雜無序的非均勻環境下粒子運動所引發的,不同的介質能夠使歷史速度產生不同的記憶時間,而在類似于該周期勢的多穩態系統中利用記憶效應將有助于增強隨機共振行為.

為分析隨機共振和驗證理論結果的有效性,數值計算了系統(1)的功率譜密度,如圖3 所示,其中選擇103條樣本軌跡,采樣頻率Fs=100 Hz 以及數據長度N=107.從圖3(a)中看到,功率譜密度在適中的溫度值(T=3)處呈現出顯著的峰值,且峰值對應的頻率值(f=0.00101)近似等于外部周期信號的驅動頻率ω,而在一定的低溫(T=0.4)和高溫(T=50)下峰結構均減弱甚至消失.這說明存在最優溫度可使得系統出現隨機共振現象,從而導致噪聲背景下的信號功率譜明顯增加.由于周期勢系統具有無窮多個平衡點,所以需要足夠大的最優溫度才能確保粒子連續地穿越勢壘,出現與驅動頻率相一致的共振同步現象.此外,在給定的溫度下,圖3(b)揭示了功率譜密度的峰值隨著記憶時間τc的增加而逐漸升高,表明記憶阻尼的存在可優化周期勢系統的信號放大性能,增強隨機共振效應,這與圖2 中的理論結果相一致.

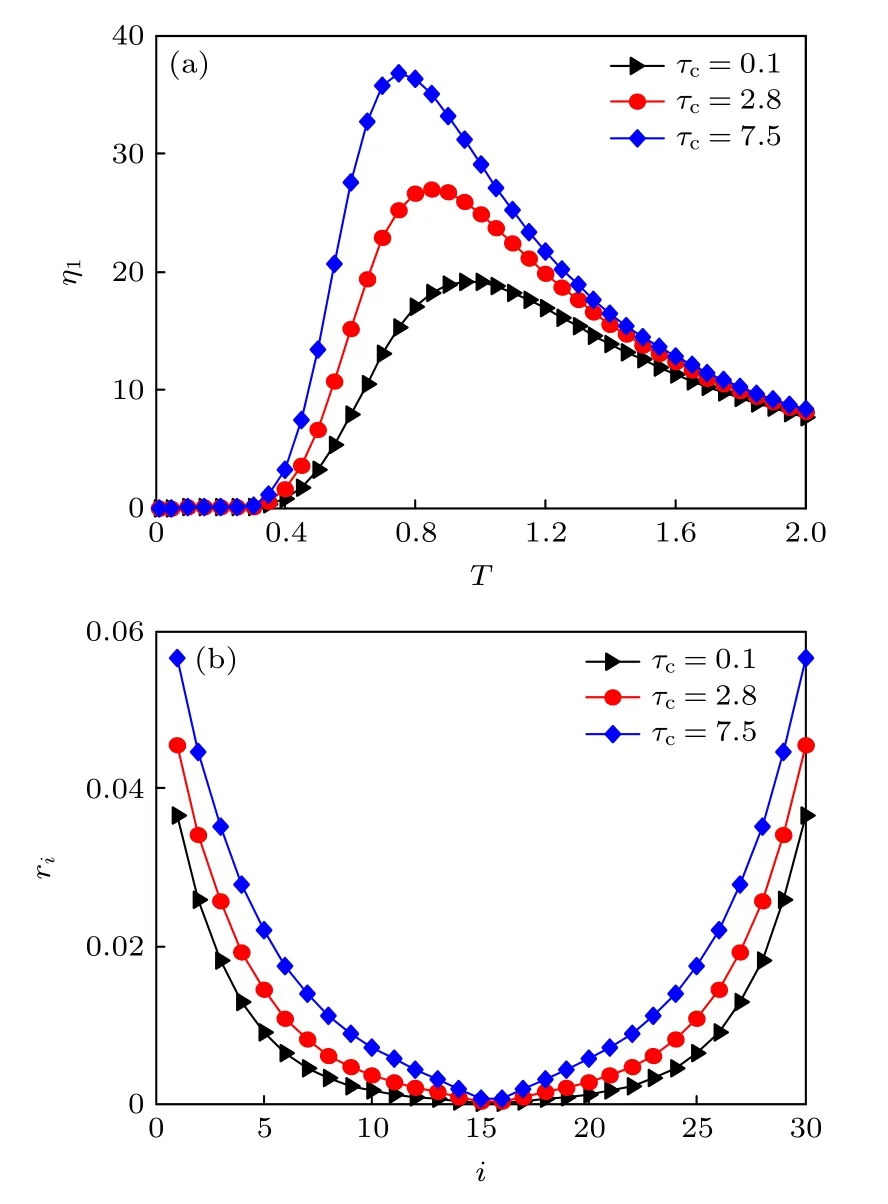
圖2 記憶時間 τc 對隨機共振的影響 (a) 功率譜放大因子 η1 隨溫度T 的變化曲線(n=6);(b)第i 個穩態點對應的響應振幅 ri 的變化曲線.其他參數取值為 Γ=4,γ0=1,ω=0.001 和m0=1Fig.2.The effects of memory time τc on stochastic resonance:(a) Spectral amplification η1 versus temperature T;(b) amplitude of the response ri versus i.Other parameter values are chosen as Γ=4,γ0=1,ω=0.001 and m0=1.

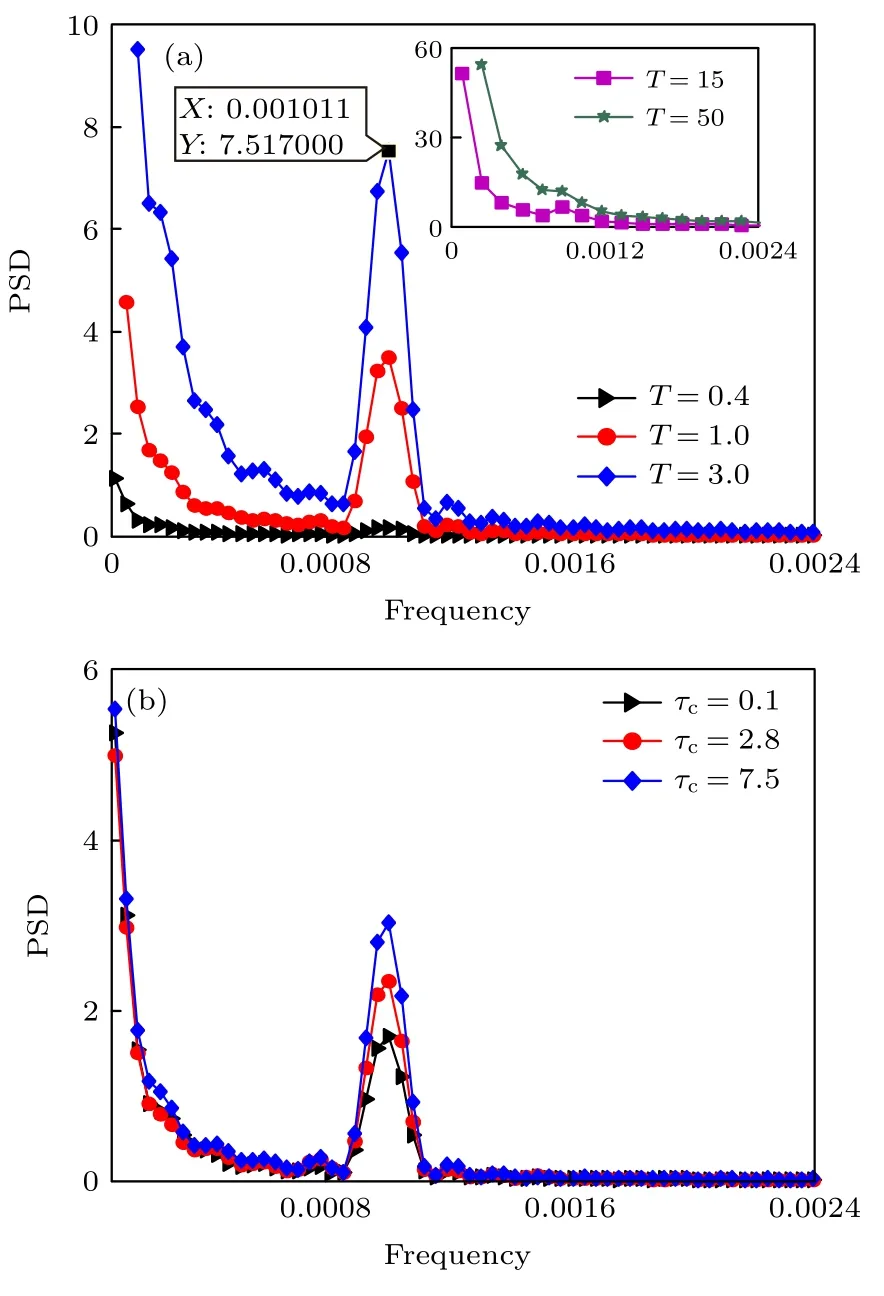
圖3 功率譜密度(PSD)作為頻率的函數曲線 (a)不同的溫度T 和 τc=1 ;(b)不同的記憶時間 τc 和 T=0.75 .其他參數取值為 Γ=4,γ0=1,ε0=0.3,ω=0.001 和m0=1Fig.3.Power spectrum density (PSD) of the system as a function of frequency with different values of (a) temperature T (τc=1);(b) memory time τc (T=0.75).Other parameter values are chosen as Γ=4,γ0=1,ε0=0.3,ω=0.001and m0=1 .

在圖4 中,分析了周期勢函數的穩態點個數n對功率譜放大因子η1以及響應振幅r1和r2的影響.從圖4(a)中可觀察到,曲線η1?T的峰值隨著n的增加顯著上升,且共振峰位置向T增加的方向移動.可見,穩態點數量的增多能夠明顯增強隨機共振現象.由于多穩態系統中兩個邊界穩態點之間的距離隨著n的增加而變大,即粒子運動的位移區間長度 2nπ 變大,因此系統在兩個最外側勢阱之間可產生更大幅度的阱間響應,同時需要足夠大的溫度,這與圖3(a)中的分析一致.故在多穩態系統中,通過適當增加穩定狀態的數量,隨機共振現象將能夠在較大的噪聲強度處發生并顯著增強,從而有效提升強噪聲環境中弱信號的探測能力.在圖4(b)中,繪制了邊界穩態點s1對應的最大響應振幅r1隨溫度的變化曲線,其峰值隨著n的增加而下降,相反于圖4(a)中功率譜放大因子的變化趨勢.這是由于在給定的激勵條件下,隨著兩個邊界穩態點之間的距離變大,粒子到達最外側勢阱的概率逐漸減小,響應振幅減弱.但在圖4(c)中,穩態狀態s2對應的響應振幅r2,其峰值隨n的增加先上升,再下降,即存在最優穩態點個數使得響應振幅最大化.這表明在噪聲和外部周期力的共同作用下,多穩態系統在不同穩定狀態之間的運動出現了更加復雜的動力學現象.值得注意的是,對于固定的穩定狀態數,功率譜放大因子和所有響應振幅均在一致的溫度值處達到局部最大值,如圖4 中標記的峰值.故在給定的多穩態系統中,兩者均可用于衡量隨機共振現象.

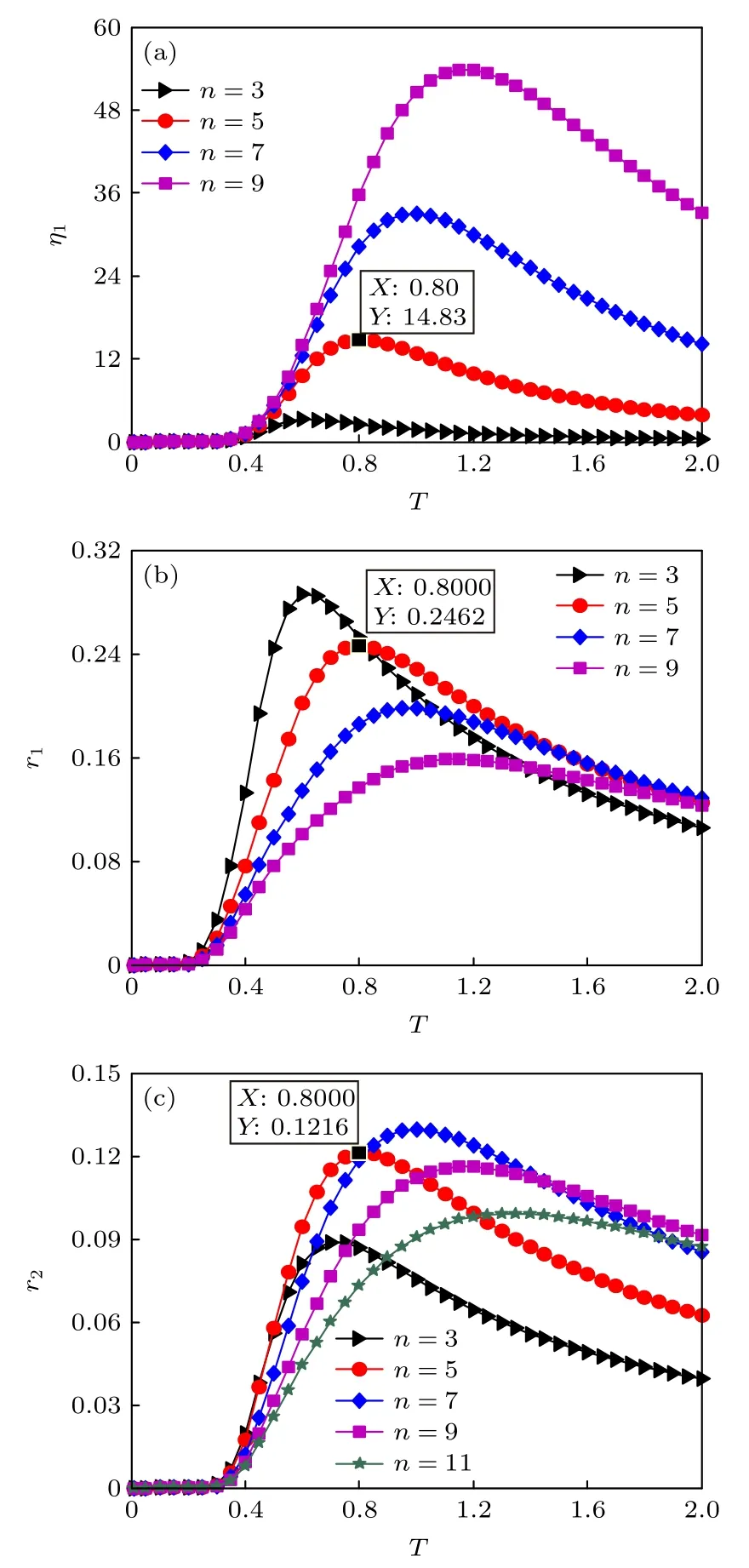
圖4 穩態點個數n 對隨機共振的影響 (a)功率譜放大因子 η1 隨溫度T 的變化曲線;(b)響應振幅 r1 隨T 的變化曲線;(c)響應振幅 r2 隨T 的變化曲線.其他參數取值為τc=3,Γ=5 ,γ0=1,ω=0.001 和m0=1Fig.4.The effects of the number of stable steady states n on stochastic resonance:(a) Spectral amplification η1 versus temperature T;(b) amplitude of the response r1 versus T;(c) amplitude of the response r2 versus T.Other parameter values are chosen as τc=3,Γ=5 ,γ0=1,ω=0.001and m0=1 .

考慮粒子在有限的范圍內運動時,穩態點數量對系統響應的影響.在周期勢U(x)=?cos(m0x)中選擇固定的位移區間,即x ∈[(2i ?1)π/m0,(2i+2n ?1)π/m0],其中i是任意整數,區間長度為 2Lπ (L=n/m0).如圖1(a)所示,通過設置m0的值可控制固定區間內系統穩態點的個數,且勢壘高度保持不變.圖5 描述了在給定的區間范圍內系統的功率譜放大因子η1隨區間內穩態點個數n的變化情況.從圖5(a)中觀察到,對于固定的區間長度L,η1隨區間內穩態點個數的增加展示了一個非單調的變化趨勢.此結果揭示了在粒子運動的區間范圍內,存在最優的穩態數量使得共振強度達到最佳,優化系統關于驅動信號的輸出響應.隨著L的增加,η1的峰值依次升高且位置向n增大的方向移動,即粒子運動的有限區間長度與其內部的穩態點數量對增強系統響應的作用表現出正相關關系.在實際環境中,受噪聲或外部信號驅動的系統,其運動通常局限在一定的區間內,考慮選取最優的穩態數量將有利于增強系統對外部弱信號的響應強度.此外,在固定的區間長度下(L=10),圖5(b)展示了記憶強度Γ對功率譜放大因子的影響.隨著Γ的增加,η1-n曲線的峰值下降且形狀趨于平緩,即隨機共振效應減弱,而共振區域變寬,同時峰值對應的穩態點數量也增多.因此,系統關于外部周期信號的響應不僅依賴于多穩態勢函數,而且與記憶性密切相關.增大的記憶強度對共振行為呈現抑制作用,但在合適數量的多穩態系統中共振現象又能得到增強.在無序的媒介或復雜的環境中,記憶強度反映了介質分子對粒子運動產生的記憶效應,合理協調記憶強度和多穩態勢函數的關系有助于提升系統的輸出.

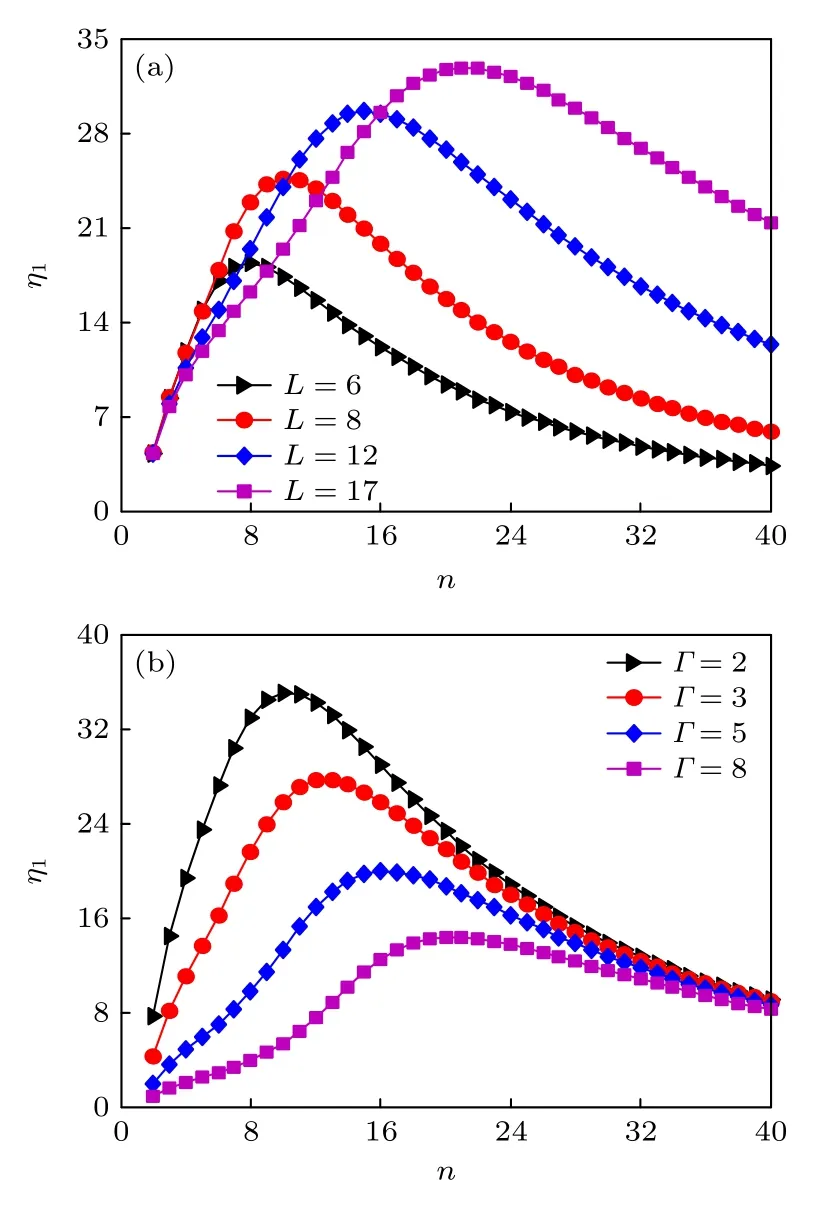
圖5 功率譜放大因子 η1 作為區間內穩態點 個數n 的 函數曲線 (a)不同的區間長度L 和 Γ=3 ;(b)不同的記憶強度Γ 和固定的長度 L=10 .其他參數取值為 τc=4 ,γ0=1,ω=0.002 和T=0.8Fig.5.Spectral amplification η1 versus the number of stable steady states n with different values of (a) interval length L (Γ=3) and (b) memory strength Γ (L=10).Other parameter values are chosen as τc=4 ,γ0=1,ω=0.002and T=0.8 .

3.2 輸入能量

周期勢系統(1)具有無窮多個平衡點,當粒子呈現出更加復雜的運動行為時,可導致系統不滿足如圖1(b)所示的多個穩態之間的躍遷情形,此時研究隨機共振需借助系統的輸入能量進行衡量.在隨機漲落的環境中,分析外部周期力對系統做的功,其隨溫度或噪聲強度的變化可反映出能量在不同狀態之間的轉換.

依據隨機能量公式[29],外部周期信號在一個周期內τω=2π/ω對系統所做的功或輸入能量W可計算為

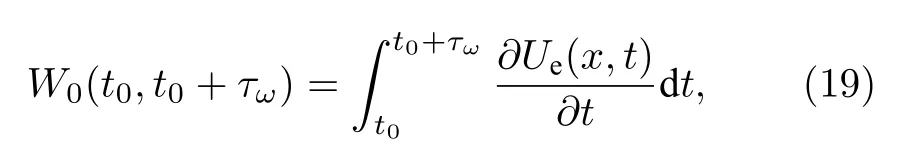
其中有效勢函數Ue(x,t)=U(x)?ε0xcos(ωt),U(x)為圖1(a)中的周期勢函數.

在給定的初始條件下,單一軌跡中N1個信號周期的平均輸入能量為

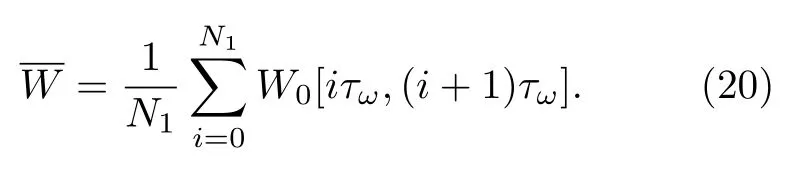
采用四階Runge-Kutta 算法對原系統進行離散化,其中信號的周期個數設置為N1=104,時間步長 dt=0.01 .在103條不同初始條件的樣本軌跡下,對相應的平均輸入能量方程(20)進行平均,最終得到所有樣本軌跡的平均輸入能量

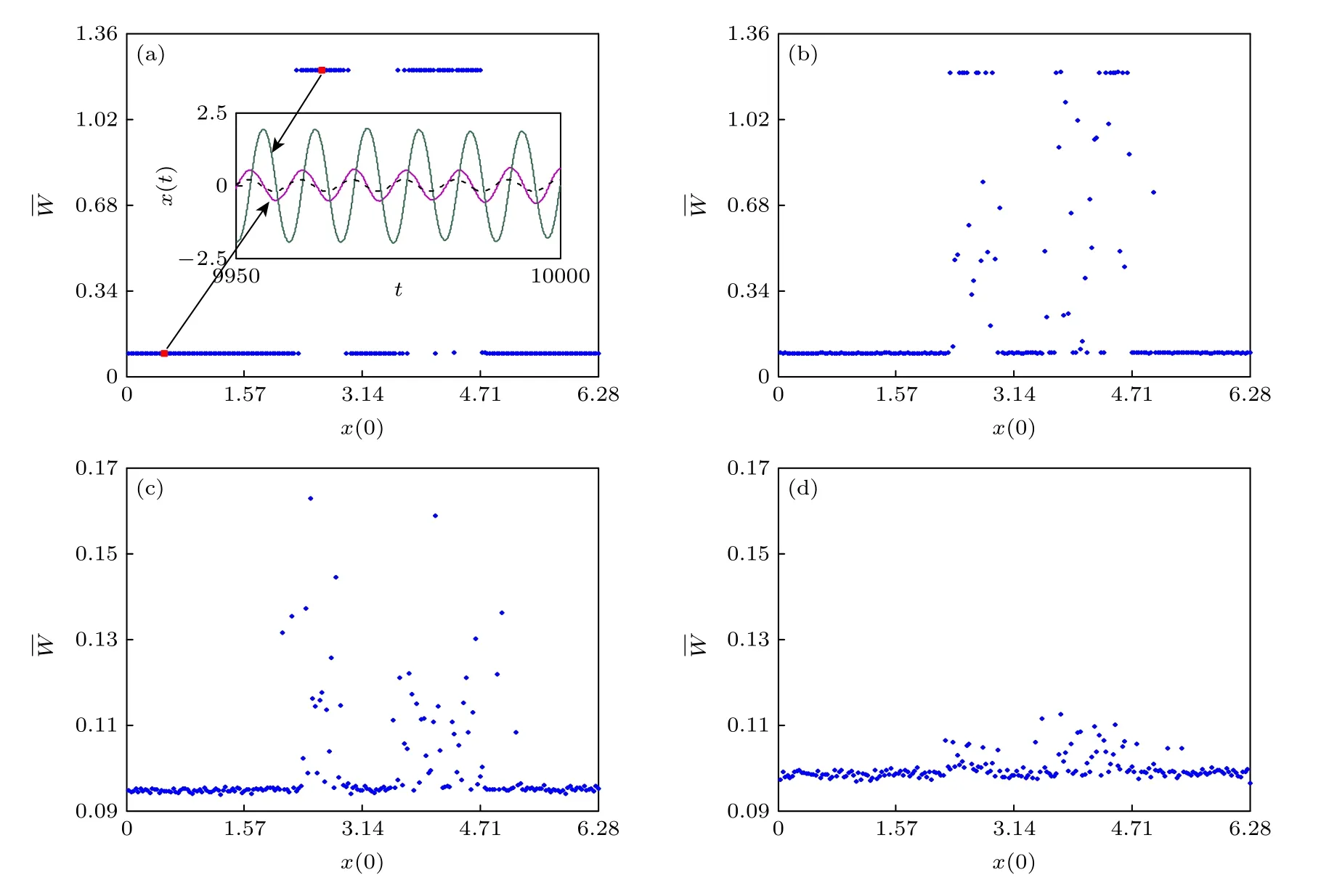
圖6 平均輸入能量 W 作為初始位置 x(0) 的函數隨不同溫度T 的變化情況,黑色線代表系統的輸入信號 ε0 cos(ωt) (a) T=0.001;(b) T=0.003;(c) T=0.009;(d) T=0.018.其他參數取值為 τc=2.3 ,γ0=0.12,Γ=0.02 和ω=π/4Fig.6.Average input energy averaged over an entire trajectory with initial position x(0) for different values of temperature T,where the black line denotes the input signal ε0 cos(ωt) :(a) T=0.001;(b) T=0.003;(c) T=0.009;(d) T=0.018.Other parameter values are chosen as τc=2.3 ,γ0=0.12,Γ=0.02 and ω=π/4 .

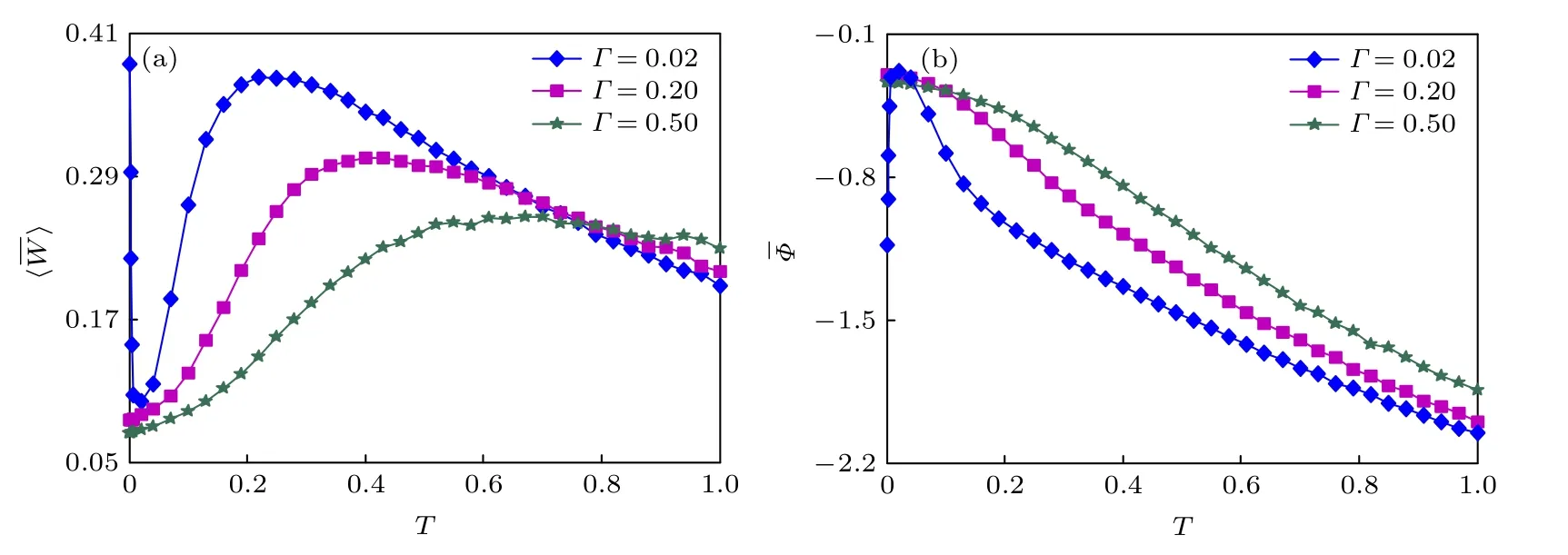
圖7 記憶強度Γ 對輸入能量的影響 (a)平均輸入能量 隨溫度T 的變化曲線;(b)相位差 隨T 的變化曲線.其他參數取值為τc=2.3 ,γ0=0.12和ω=π/4Fig.7.The effects of memory strength Γ on input energy:(a) Average input energy versus temperature T;(b) phase lag versus T.Other parameter values are chosen as τc=2.3 ,γ0=0.12 and ω=π/4 .

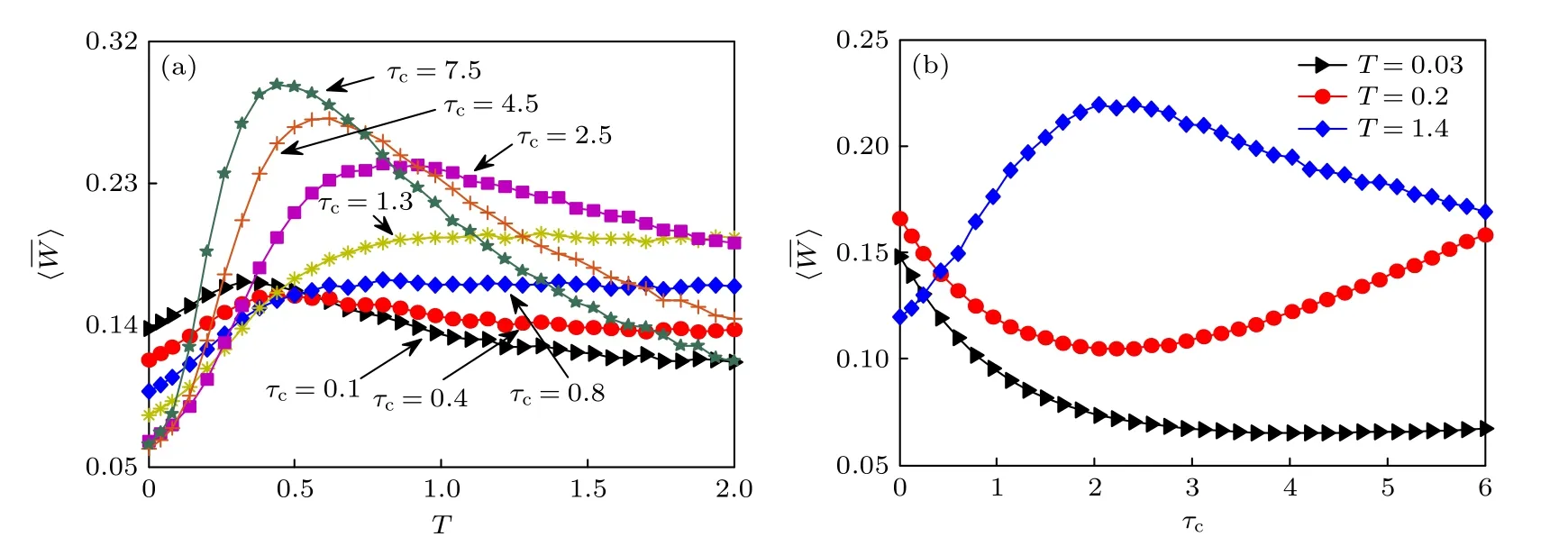
圖8 記憶時間 τc 對輸入能量的影響 (a) 隨T 的變化曲線;(b) 隨 τc 的變化曲線.其他參數取值為 Γ=0.7,γ0=0.12和ω=π/4Fig.8.The effects of me mory time τc on input energy:(a) versus T;(b) versus τc .Other parameter values are chosen as Γ=0.7 ,γ0=0.12 and ω=π/4 .

4 結論

針對廣義Langevin 方程描述的含記憶阻尼的周期勢系統,主要研究了該系統在外部周期力作用下的隨機共振.由于系統的多穩態特征和non-Markovian 性質導致理論分析困難,故引入變量變換將原始的non-Markovian 模型等價轉化為多維Markovian 系統.根據線性響應理論,推導出了適用于一般多穩態模型的功率譜放大因子,揭示了記憶效應和多穩態特征對隨機共振的影響,并得到數值結果的驗證.分析表明,記憶時間的延長和穩態數量的增多均對共振行為有增強作用,但誘導共振產生的溫度變化不同.對于固定的系統位移區間,存在最優穩態點數量使得共振效應最佳,同時記憶強度對系統輸出響應的影響依賴于穩定狀態的個數.然而,當周期勢系統呈現出更加復雜的運動行為時,通過輸入能量發現,記憶時間對隨機共振起著先減弱再增強的作用,即在適當溫度范圍內,合理控制記憶時間可優化外部周期力對系統所做的功.

本文獲得的解析結果為周期勢系統中共振現象的研究及應用提供理論指導作用.具有記憶阻尼的隨機動力系統多用于描述粒子在復雜無序的非均勻環境中運動,接下來可進一步考慮外部噪聲及與內部噪聲的互關聯性對共振行為的影響.由于周期勢系統的多穩態特征,上述隨機共振理論可有效應用于機械故障診斷中微弱信號的檢測.