HY-2B星載GPS數據質量及簡化動力學精密定軌分析

王廣哲 郭金運 郭恒洋 楊洲銘 紀 兵 彭海龍 林明森

1 山東科技大學測繪與空間信息學院，青島市前灣港路579號，266590 2 海軍工程大學導航工程系，武漢市解放大道717號， 430032 3 國家衛星海洋應用中心，北京市大慧寺路8號，100081

HY-2B衛星是我國第2顆極軌海洋動力環境衛星，其將與后續發射的HY-2C和HY-2D衛星組成全球大中尺度海洋動力環境衛星監測體系[1]。高精度的軌道是HY-2B衛星海洋測高和重力場模型反演的基礎[2]，因此有必要對HY-2B衛星的定軌方法和策略進行研究。

低軌衛星精密定軌方法主要可以分為3類：運動學定軌、動力學定軌和簡化動力學定軌[3-4]。利用星載GPS數據進行定軌具有精度高、全天時、連續性的特點，目前已被廣泛應用[5]。衛星天線相位中心偏差(PCO)和相位中心變化(PCV)是影響定軌精度的重要誤差源。在衛星發射前可以得到先驗PCO、PCV值，但因衛星發射過程中受力復雜、燃料消耗等因素的影響，實際值與先驗值之間會發生較大的變化，因此在軌估計PCO、PCV模型對于定軌結果有較大的影響。數據質量是影響定軌結果的重要因素之一，也是高精度衛星定軌的可靠保障。衛星可見性、周跳比、多路徑效應、觀測數據的完整性是衡量數據質量的重要標準。

本文利用Anubis軟件對HY-2B衛星數據進行質量分析及簡化動力學定軌，通過分析不同時間間隔和先驗值組合下的SLR結果，尋找出最優偽隨機脈沖先驗值，并通過載波相位殘差、重疊軌道比較、SLR檢核3種方法檢驗其定軌精度；再使用直接法估計出不同分辨率的PCV改正模型，并加入到定軌過程中，分析其對定軌結果的影響，得到高精度的衛星定軌結果。

1 數據處理策略

利用2020-12-15～21(doy350～356)的HY-2B星載GPS數據和CODE提供的精密星歷EPH、極移ERP、鐘差CLK等參數，定軌弧段為24 h，采用簡化動力學定軌方法[5]解算HY-2B衛星的精密軌道，尋找HY-2B衛星的最佳偽隨機脈沖值，分析不同分辨率PCV對于定軌精度的影響。

基于Bernese5.2軟件對HY-2B衛星進行簡化動力學精密定軌研究[6]，并利用表1中的力學模型消除HY-2B衛星運行時受到的保守力和非保守力的影響。

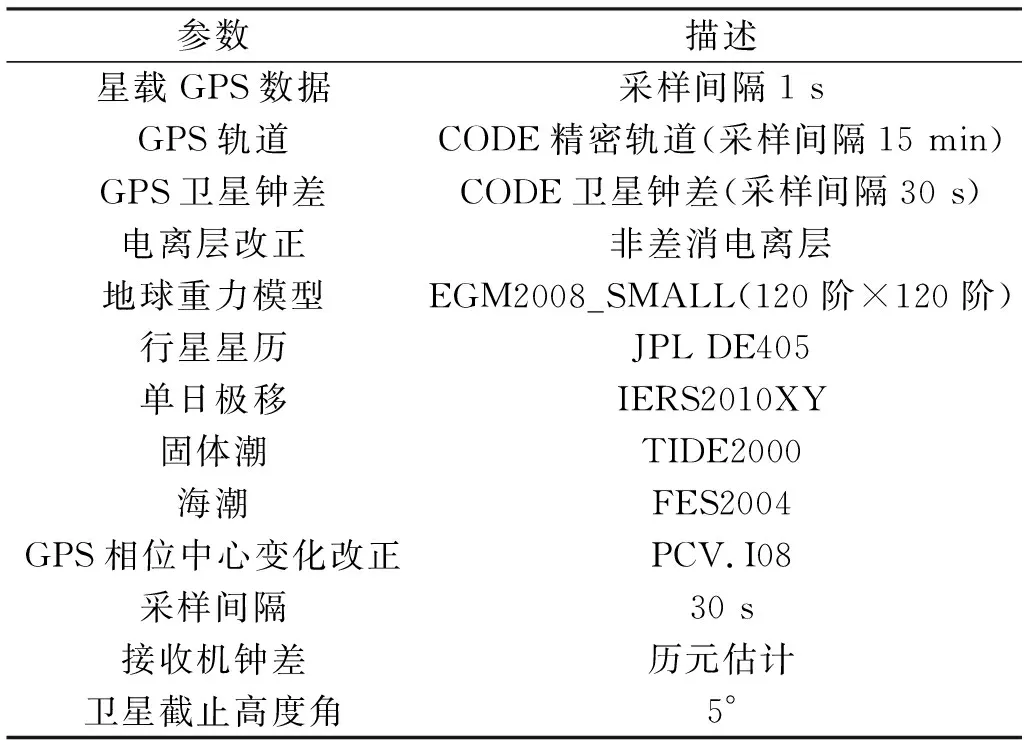
表1 HY-2B衛星簡化動力學定軌策略[7]Tab.1 Reduced-dynamic orbit determination strategy for HY-2B satellite

以HY-2B衛星2020年doy350的星載GPS數據為例研究不同的隨機脈沖時間間隔和先驗標準差對定軌結果的影響。時間間隔分別設置為6 min、9 min、12 min、24 min、60 min，先驗標準差分別取1×10-3m/s、1×10-4m/s、1×10-5m/s、1×10-6m/s、1×10-7m/s、1×10-8m/s、1×10-9m/s、1×10-10m/s，使用不同的時間間隔和先驗標準差組合計算HY-2B衛星軌道，并用SLR檢查定軌精度。

星載GPS數據是GPS衛星天線瞬時相位中心到低軌衛星信號接收時刻瞬時天線相位中心的距離。精密軌道的參考點是衛星質心，由于衛星發射及運動中某些因素的影響會導致相位中心發生改變。本研究重新校準了不同分辨率的PCV，并與不添加PCV的定軌結果進行比較。使用PCV直接法對7 d星載GPS數據進行PCV在軌估計，該方法在定軌過程中把未知參數PCV代入觀測方程，同時估計軌道參數和PCV，根據最小二乘原理，求得多天PCV并取平均作為最終改正值，受接收機鐘差等因素影響較小。

2 數據質量分析

2.1 衛星可見性

圖1(采樣間隔30 s)為HY-2B衛星在2020年doy350～356的衛星可見數。統計可得，觀測到3顆及以下衛星的歷元占總歷元的0.67%，觀測到4顆及以上衛星的歷元占總歷元的99.33%，觀測到5顆及以上衛星的歷元占總歷元的94.54%，觀測到6顆及以上衛星的歷元占總歷元的78.11%。大部分時間HY-2B衛星能夠觀測到6顆及以上的衛星，接收機性能良好且穩定。

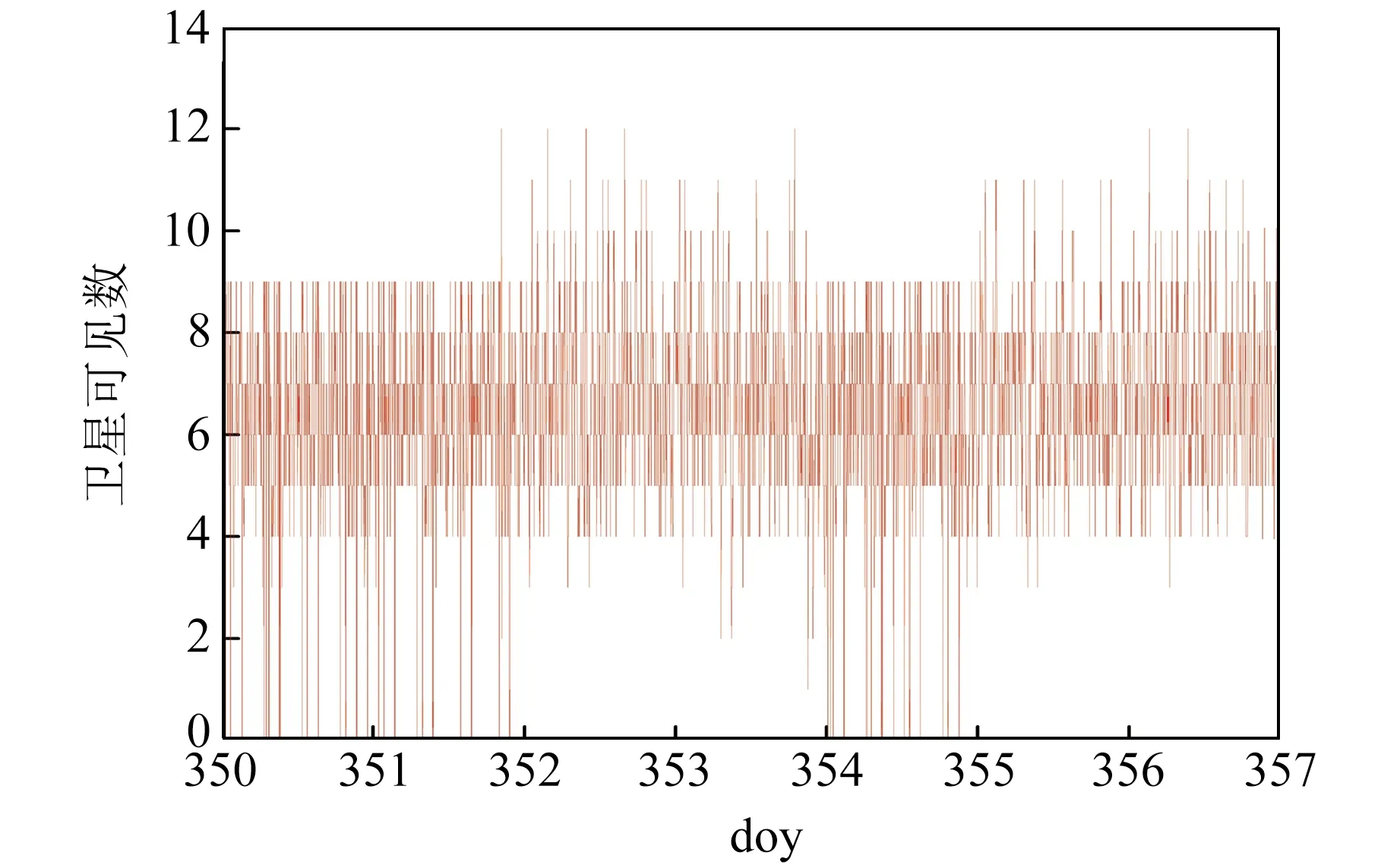
圖1 HY-2B衛星衛星可見數Fig.1 Visible satellite numbers of HY-2B satellite

2.2 周跳比、數據完整率、數據利用率和多路徑誤差

周跳比(o/slps)表示在一定時間內實際觀測到的歷元數與發生周跳的歷元數之比。數據完整率是GPS接收機在一定時間內獲取的實際歷元數與理論歷元數之比。數據利用率是同時觀測到含有4顆以上雙頻觀測值的衛星歷元數和預期歷元數之比[8]。數據完整率和利用率可以反映接收機獲取數據的能力和外部環境的優劣。

表2為HY-2B衛星GPS數據質量評估結果。可以看出，MP1的RMS值均大于MP2，L1多路徑誤差RMS均值為15.7 cm，L2多路徑誤差RMS均值為9.5 cm，周跳比均值為30，數據完整率均值為99.65%，數據利用率均值為98.66%。

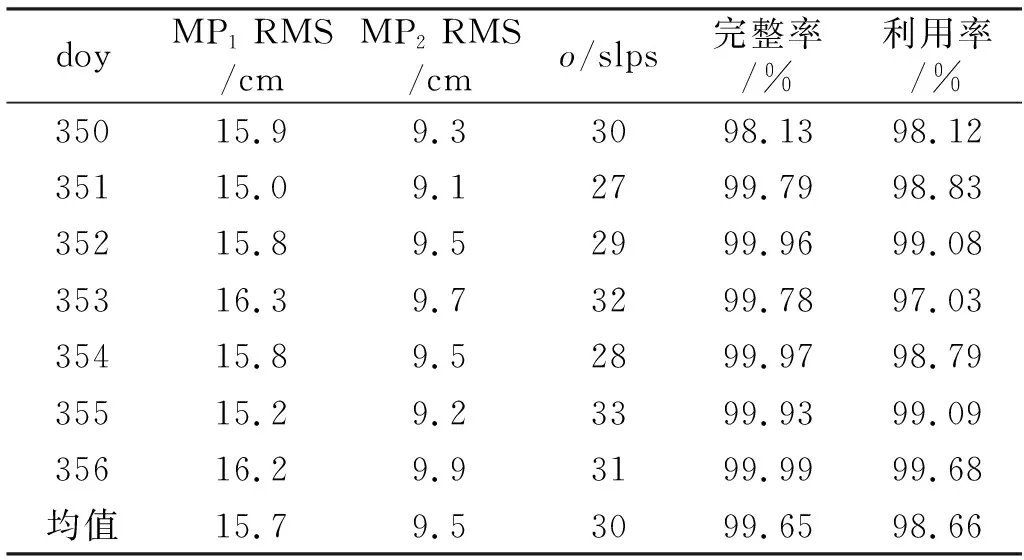
表2 HY-2B衛星數據質量評估Tab.2 Data quality assessment of HY-2B satellite

圖2反映了2020年doy350 G03衛星L1、L2波段的多路徑誤差和高度角的關系。可以看出，隨著高度角的降低，多路徑誤差不斷增加。高度角小于40°時，多路徑誤差顯著提升；高度角較大時，多路徑誤差明顯減小，且MP1大于MP2。

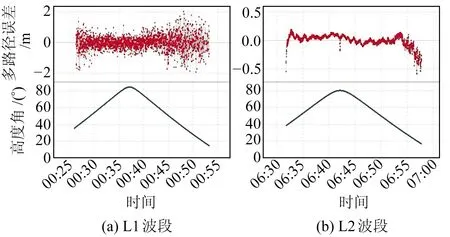
圖2 G03衛星多路徑誤差和高度角的變化Fig.2 Multipath errors and elevation angle changes of G03 satellite

2.3 電離層延遲變化率

當2個頻率的載波數據傳播路徑相同時，電離層延遲可表示為：

式中，f1、f2為載波的頻率，λ1、λ2為載波的波長，N1、N2為整周模糊度，M1、M2為載波的多路徑效應，L1、L2為載波相位觀測值。

利用相鄰歷元的電離層延遲可得到電離層延遲變化率(IOD)，當IOD>4 m/min時，認為電離層發生跳變。圖3、4分別為doy356 07：30～9：00的電離層延遲以及電離層延遲變化率，載波相位觀測數據的中斷導致周跳發生頻率較大，因此在觀測時段末尾會出現一個突變(圖4中棕色到藍色)。可以看出，G01、G08、G18、G24、G29的GPS觀測數據中，周跳的發生頻率較大。

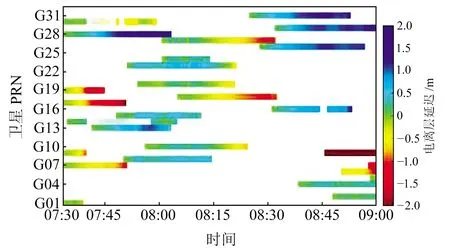
圖3 電離層延遲Fig.3 Ionospheric delay

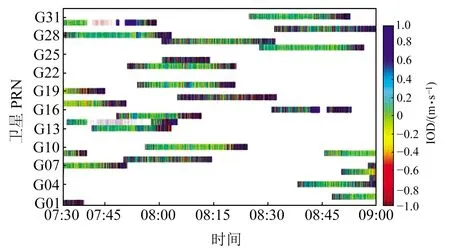
圖4 電離層延遲變化率Fig.4 Ionospheric delay rate

3 HY-2B衛星定軌結果與精度分析

采用載波相位殘差和重疊軌道檢驗對HY-2B衛星定軌結果進行內符合精度評估，采用SLR檢核方法進行外符合精度評估。

3.1 隨機脈沖對簡化動力定軌的影響分析

在不同的偽隨機脈沖時間間隔和先驗值情況下進行定軌，并使用SLR進行檢核得到RMS值，定軌精度如表3(單位 mm)所示。在低軌衛星精密定軌的過程中，隨著衛星高度的不同所采用的時間間隔一般設置為6～60 min。這是因為當時間間隔大于60 min時，整體定軌精度較差，無參考意義；當時間間隔小于6 min時，定軌精度不再提高且所用時間會大幅增加[9]。

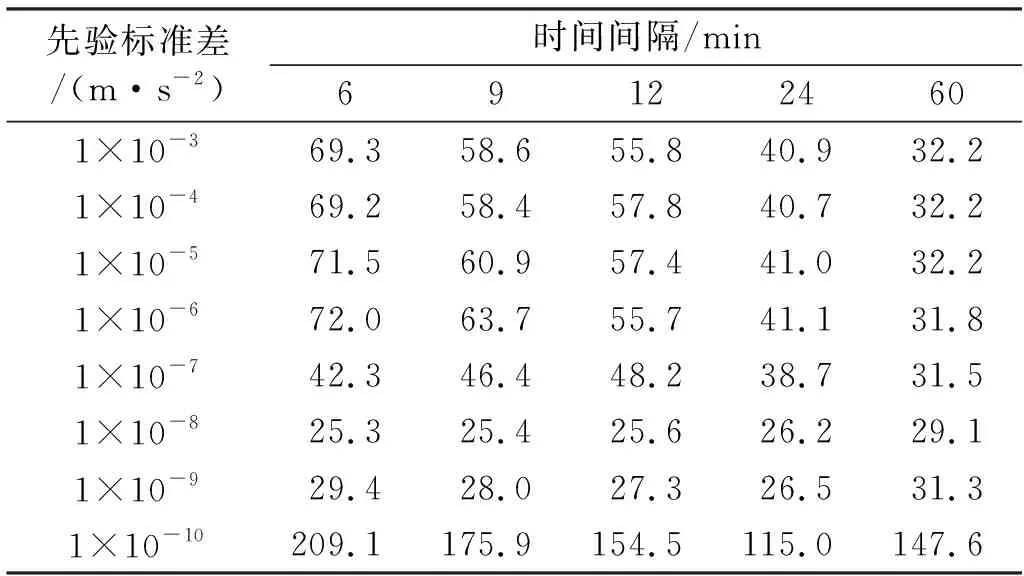
表3 不同偽隨機脈沖時間間隔和先驗值組合下HY-2B衛星定軌SLR檢核RMS值Tab.3 RMS values of HY-2B satellite orbit determination SLR check under different combinations of pseudo-random pulse time intervals and prior values

表3表明：1)在所有時間間隔下，當先驗標準差為1×10-8m/s2時，定軌精度都是最高的。2)在相同時間間隔下，先驗標準差在1×10-3～1×10-6m/s2變化時，定軌精度變化較小；當先驗標準差為1×10-7m/s2時，定軌精度明顯提升；當先驗標準差為 1×10-8m/s2時，定軌精度最高，之后開始下降；當先驗標準差從1×10-9變為1×10-10m/s2時，定軌精度大幅降低。綜合以上結論，本次HY-2B簡化動力學精密實驗采用脈沖時間間隔為6 min，先驗標準差為1×10-8m/s2。

3.2 載波相位殘差分析

用消電離層組合(LC)對HY-2B星載GPS數據進行處理，統計2020年doy350～356的簡化動力學定軌相位殘差值，結果如表4(單位mm)所示。

從表4可以看出，HY-2B衛星7 d的載波相位殘差在7.4～7.9 mm之間，波動很小。說明本次實驗采用的計算模型符合實際情況，HY-2B衛星搭載的GPS接收機能夠獲取穩定的數據，獲得可靠的定軌結果。

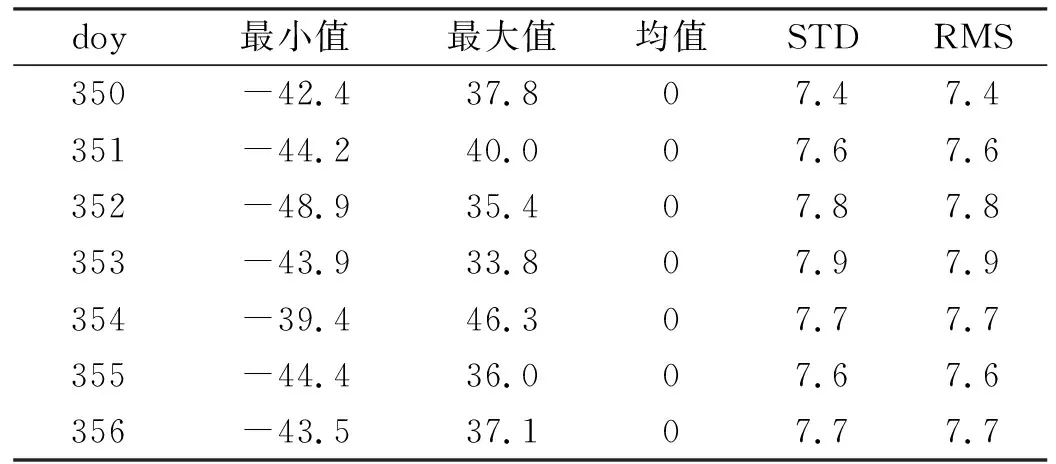
表4 載波相位殘差統計Tab.4 Carrier phase residual statistics

3.3 重疊軌道檢驗

使用2020年doy350～356的星載GPS數據進行簡化動力學重疊軌道的對比，把每天的數據分為2個弧段分別進行定軌，第1段為00:00～18:00，第2段為12:00～24:00，選取13:00～17:00 共4 h的重疊弧段進行比較，結果如表5(單位mm)所示。可以看出，徑向(R)RMS均值為7.6 mm，切向(T)RMS均值為12.4 mm，法向(N)RMS均值為9.8 mm，3D RMS均值為17.5 mm，證明了HY-2B星載GPS數據具有較高的精度和穩定性，定軌精度能夠達到cm級。

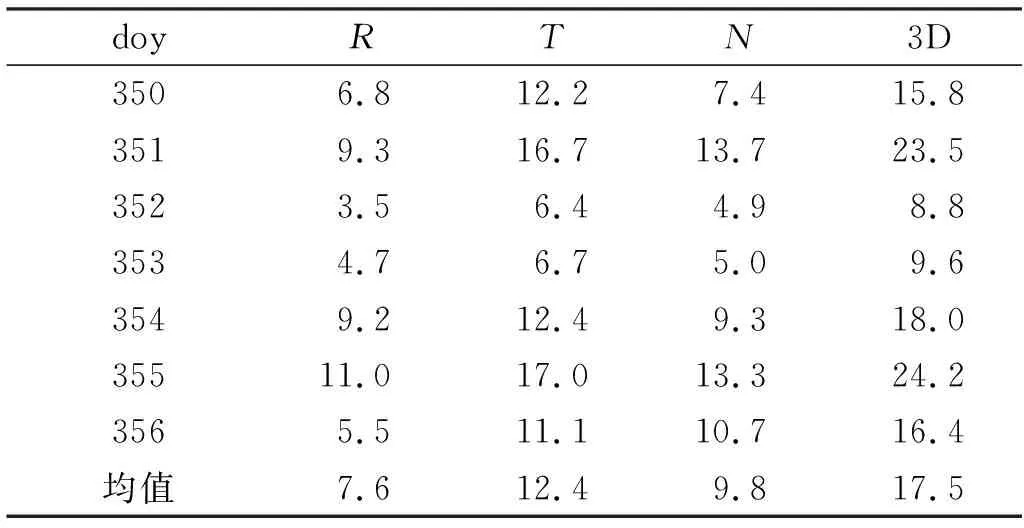
表5 重疊軌道RMS值對比Tab.5 RMS values comparison of overlap orbits

3.4 PCV模型

在Bernese軟件中，天線相位中心變化可以表示為：

Δφ(α,z)=Δφ′(α,z)+Δre

(2)

式中，Δφ(α,z) 是衛星和接收機之間幾何距離的總相位中心校正，α、z是衛星星固坐標系下的衛星方位角和高度角，Δr是平均天線相位中心和天線參考點之間的位置改正，e是接收機天線到衛星方向上的單位矢量。

圖5是在軌估計出的10°× 10°和5°× 5°的PCV格網模型。假設每個格網點都是未知的，直接計算出每一個格網的值，則得到的模型更為精細化，模型圖以斑點狀顯示。可以看出，當高度角較低時，PCV絕對值較小；當高度角為80°～90°時，因只有很少的觀測數據，導致計算的PCV值出現“空洞”。

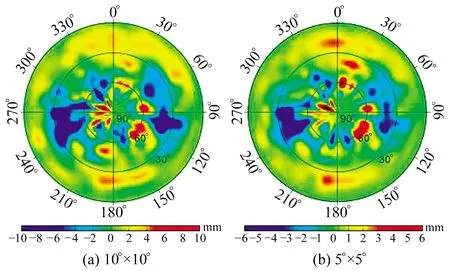
圖5 PCV模型Fig.5 PCV model

3.5 SLR檢核

SLR檢核是目前驗證定軌結果的最精確手段[10]。大多數低軌衛星都搭載了SLR反射棱鏡，測距精度優于1 cm[11]。

利用國際激光測距服務組織(ILRS)提供的HY-2B衛星SLR數據驗證定軌精度。在doy350～356期間，共有16個測站對HY-2B衛星進行觀測，得到935個標準點(normal point, NP)數據，刪除數據很少且質量較差的1873和7403測站，對剩下的NP數據進行計算。從表6(單位mm)可以看出，加上PCV模型后，每天SLR檢核精度均有提升，且對于越差的結果改善效果越好；不加PCV模型7 d RMS均值為27.8 mm，加上10°× 10°和5°× 5° PCV模型后，7 d RMS均值分別為26.9 mm和26.6 mm，精度分別提高0.9 mm和1.2 mm。證明估計出的PCV模型對于定軌精度的提升具有重要意義，簡化動力學定軌結果符合精度要求。

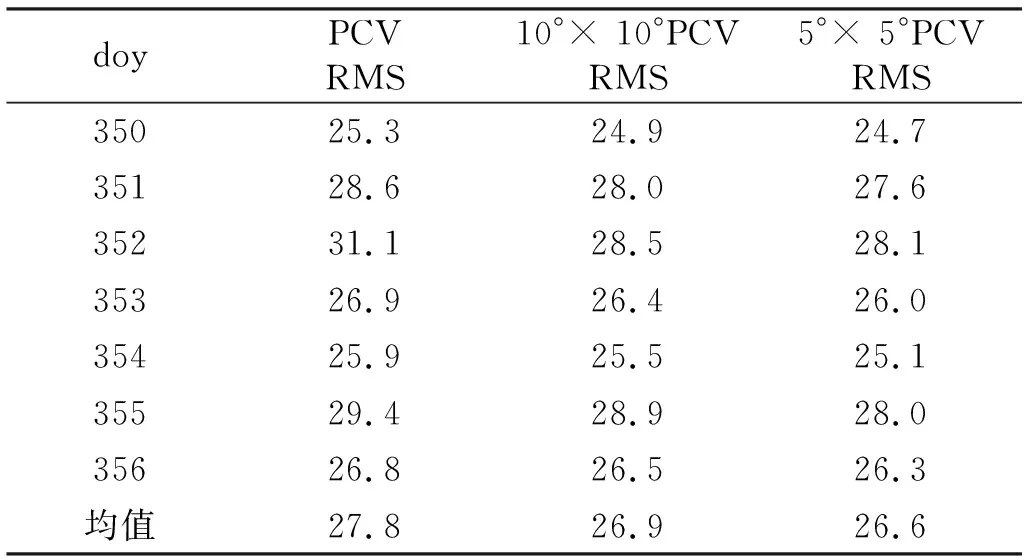
表6 加PCV模型后HY-2B衛星軌道SLR檢核結果Tab.6 SLR check results of HY-2B satellite orbit after adding PCV models

通過以上分析可以證明，HY-2B衛星的星載GPS接收機性能較強、數據穩定、觀測質量較高。

計算剩余14個測站7 d的SLR檢核結果，和測站的NP數據一并列出(圖6，圖中所加PCV模型為5°×5°)。由圖6可見，7090測站NP數據最多，達到229個，占總數據量的25.5%，不加PCV模型時RMS為20.6 mm，加上5°× 5° PCV模型后RMS降低為19.2 mm。7824和7249測站精度較差，兩者共有NP數據12個，占總數據量的1.3%，不加PCV模型時RMS分別為59.2 mm和43.5 mm，加上PCV模型后精度提高到40.2 mm和42.4 mm。精度最高的測站是7941，共有23個NP數據，加入PCV模型后RMS為18.7 mm。大部分測站的RMS低于40 mm，符合預期要求。

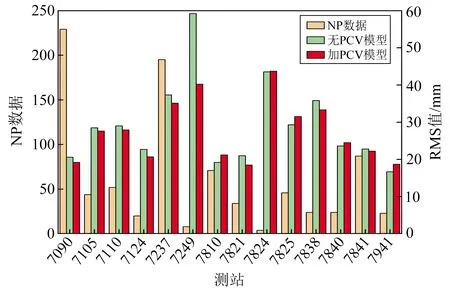
圖6 NP數據與SLR檢核各測站RMS值Fig.6 NP data and RMS values with SLR check of each station

4 結 語

1)HY-2B衛星7 d衛星可見數均值為6.68顆，L1多路徑誤差RMS均值為15.7 cm，L2多路徑誤差RMS均值為9.5 cm，數據完整率為99.65%，數據利用率為98.66%，o/slps為30。證明HY2接收機性能良好，獲取的數據穩定。

2)通過分析不同時間間隔和不同先驗值的偽隨機脈沖參數下的定軌結果，最終選取脈沖時間間隔6 min、先驗標準差1×10-8m/s2作為實驗的脈沖先驗值進行后續定軌任務。

3)HY-2B衛星2020-12-15～21的7 d載波相位殘差在7.4～7.9 mm波動，變化幅度較小。證明衛星觀測數據的擬合性較好，采取的力學模型符合實際情況，在解算的過程中能有效地消除保守力和非保守力的影響，得到穩定的定軌結果。重疊軌道實驗結果表明，R方向RMS為7.6 mm，T方向RMS為12.4 mm，N方向RMS為9.8 mm，3D RMS為17.5 mm，內符合精度達到cm級。

4)利用SLR觀測數據進行外符合精度檢核，無PCV模型改正時，簡化動力學定軌精度達到27.8 mm；加入估計得到的5°× 5° PCV模型后，整體檢核精度提高1.2 mm。證明估計的PCV模型對提高定軌精度具有重要意義。本次實驗的外符合精度也達到cm級，符合預期要求。

致謝：感謝國家衛星海洋應用中心提供數據支持。