挖掘教材,培養學生的“讀思達”能力

胡惠顏 黃愛平

摘要：教材是教師的教、學生的學的主要載體和依據，教學過程中，通過挖掘教材正文的內容、例題、課后的習題等顯隱性資源，有效地培養學生的“讀思達”能力，促進學生核心素養的形成和發展.

關鍵詞：初中數學教材；挖掘運用；“讀思達”能力

數學教材是教材編研人員根據國家對基礎教育的定位、當代科技進步與社會發展狀況的要求，同時結合學科的特點、社會文化、藝術、生活的需求、學生的年齡特點等編寫出來的.教材中的內容、例題、習題都是經過了教材編研人員的精心選擇編制，是教材編研人員集體智慧的結晶，它的作用主要是為教學活動提供一個必要的準則和依據［1］.教師作為教學活動的執行者，必須根據課程標準要求和學生的認知水平，充分把握教材編委們留下的“教材運用創造空間”，挖掘、整合運用教材的顯隱性課程資源，形成新的課程學習資源，明白要教什么、怎么教、教到什么程度，學生學什么、怎么學、學習目標是什么［2］，才能合理高效地運用教材.因此，在“雙減”背景下為了切實提高課堂教學效率，充分挖掘并運用教材，培養學生的“讀思達”能力，顯得尤為重要.

何謂“讀思達”能力？讀就是閱讀.數學的閱讀不同于語文、英語學科的閱讀，不僅要讀懂教材文本中的定義、定理、法則、性質、例題、習題等閱讀材料，還要懂得在閱讀的過程中把文字語言、符號語言和圖形語言進行相互轉換.“思”就是運用數學思想方法進行分析思考、探究理解、感悟.通過課堂教學揭示數學定義、定理、法則、性質的形成和發展過程，引導學生理解、認識數學的本質，掌握數學知識，感悟數學美，獲得數學學習的愉悅感.“達”就是數學語言表述、規范的書面解答.數學語言是指對數學概念、算式、公式、運算、運算定律、法則及解題思路、推理過程等的表述，有文字語言、符號語言、圖形語言，具有嚴密、準確、簡練、抽象、符號化及嚴謹的邏輯推理等特點.蘇聯數學教育家斯托利亞爾說過：“數學教學也就是數學語言的教學.”因此，在日常的課堂教學中，培養學生規范的數學語言表述就要從培養學生的“達”開始.

下面，筆者以北師大版初中數學教材為例，漫談如何挖掘并利用教材的顯隱性課程資源，培養學生的“讀思達”能力.

1 科學設計課堂教學環節

在課堂教學中，培養學生“讀思達”能力的各個環節應當是相互交錯、互相滲透、相輔相成的.以北師大版數學九年級下冊第三章第五節“直線和圓的位置關系”為例，淺析課堂教學“讀思達”能力的培養.

案例1“直線和圓的位置關系”新授課教學片段

第一個環節：引讀導達引思.

引讀：讓學生閱讀書本第89頁的內容.

導達：讓學生動手在紙上畫一個圓，把直尺的一邊看作直線，移動直尺，根據直尺移動時與圓的各種位置情況，畫出圖形.

引思：直線和圓有幾種位置關系？有幾個公共點？最多幾個點？最少幾個點？

導達：

（1）師生共同歸納總結出直線和圓的三種位置關系，并讓學生理解掌握切線的定義.

（2）下列各題是否正確？請說明理由.

①直線和圓最少有兩個公共點；（）

②如果直線與圓相切，那么直線和圓只有一個公共點；（）

③如果A，B是⊙O外的兩點，那么直線AB與⊙O相交.（）

引思：由練習題的解答進一步理解“直線和圓的位置關系”，并引導學生思考能否類比“點和圓的位置關系”進行數量分析.

引讀：讓學生閱讀書本第66頁的“想一想”這部分內容.

引思：類比“點和圓的位置關系”，如果⊙O的半徑為r，圓心O到直線l的距離為d，那么直線和圓的位置關系如何用r與d的大小關系來表達？反之，如何根據r與d的大小關系來確定直線和圓的位置關系？

導達：由上面的思考和類比，利用數形結合思想，鼓勵學生用r與d的數量關系，歸納總結出直線與圓的位置關系的性質和判定.

引讀：讓學生閱讀并完成書本第89～90頁的“想一想”.

引達：讓學生完成下面填空題.

①已知⊙O的半徑為5 cm，圓心O到直線a的距離為3 cm，則⊙O與直線a的位置關系是，直線a與⊙O的公共點有個.

②已知⊙O的半徑為4 cm，圓心O到直線a的距離為4 cm，則直線a與⊙O的位置關系是，直線a與⊙O有個公共點.

③若⊙O的半徑為r，且圓心O到直線a的距離為5，則r的取值范圍是時，⊙O與直線a相交.

④直徑為a的一枚硬幣沿著直線滾動一圈，圓心的運動軌跡長為.

第二個環節：由思、達引讀.

通過第一個環節的教學，學生理解并掌握直線與圓的三種位置關系，理解“圓心到直線的距離與半徑之間的數量關系”和“直線與圓的三種位置關系”的對應與等價關系.在此基礎上，讓學生閱讀書本第89頁的三幅圖（圖1），教師利用多媒體動畫播放：太陽從海平面冉冉升起，上升過程中與海平面呈現的位置關系.

在此基礎上，教師還可以引導學生朗讀唐朝王維的《使至塞上》：“單車欲問邊，屬國過居延.征蓬出漢塞，歸雁入胡天.大漠孤煙直，長河落日圓.蕭關逢候騎，都護在燕然.”讓學生在朗讀中，欣賞“大漠孤煙直，長河落日圓”的美麗景象，體會圖1所蘊涵的數學意境——直線與圓的位置關系，在欣賞美景詩詞中感悟數學美，培養學生用數學的眼光觀察世界［1］.

2 運用教材的“問題解決”內容

北師大版教材的編排特點是螺旋式上升，由淺入深，從易到難，配有大量的議一議、做一做、想一想、數學理解、問題解決、聯系拓廣等［3］.教師作為使用這套教材的執行者，應當充分挖掘并運用教材的這些資源培養學生的“讀思達”能力.

案例2八年級上冊第174頁的“問題解決”

北師大版八年級數學上冊最后一章“平行線的證明”第三節“平行線的判定”，是初中階段數學演繹推理、規范表達的示范課.這節課學生才真正接觸到文字命題題型的證明，是一節幾何演繹推理的入門課.演繹推理對于學生來說是一個嶄新的學習內容，學生會感到困難甚至無所適從.因此，在入門教學時對學生的學習方法進行指導，引導他們進行“讀思達”顯得尤為重要.案例2是這節課課后習題7.4的最后一道題目，是一道幾何文字題.引導學生對這道題目進行“讀思達”，能有效地鞏固“平行線的判定”這節課的演繹推理和數學語言的規范表達.

第一環節：引讀、激思、導達.

引讀：①首先引導學生讀題，對題目的關鍵字、詞、句要標識、標注，加深理解、提煉.本題的關鍵字和詞有直角尺、畫、直線a和b、兩條平行線.②引導學生學會把題目分成題目的情景、所給的條件 、需要說明的問題這三部分.每一部分都要仔細讀，有條件的還要反復讀，才能把握題目的實質.本題的題目情境是木工師傅畫平行線；所給的條件是木工師傅用的工具是直角尺，也就是畫出來的兩條線都是垂直于同一條直線；需要說明的問題是這兩條直線平行.

激思：教師和學生一起分析思考本題的已知條件（已知部分）是什么，結論（求證部分）是什么，再引導學生畫出符合題意的圖形，然后根據圖形，將題目的文字語言轉化為符號語言.

導達：在引讀激思后，讓學生先用數學語言表達出本題，教師糾錯，然后師生共同用嚴謹的邏輯推理和數學語言把本題表述出來.

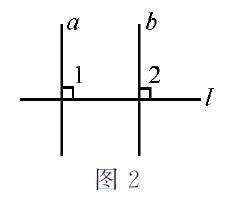
已知：直線a⊥直線l，直線b⊥直線l（如圖2）.求證：直線a∥直線b.

證明：如圖2，

∵ 直線a⊥直線l? （已知），

∴∠1=90°（垂線的定義）.

∵ 直線b⊥直線l（已知），

∴∠2=90°（垂線的定義）.

∴∠1+∠2=180°（等式的性質）.

∴直線a∥直線b（同旁內角互補，兩直線平行）.

第二個環節：由達再引讀拋思.

引讀：在第一環節的“導達”之后，要求學生重新多讀本題幾遍，讓學生明白實際生活中處處有數學問題，要用我們所學到的知識來思考、表達、理解這些數學問題［1］.

3 挖掘教材“脈絡”

深度研讀北師大版教材的編排特點，還可以發現：不同知識點的編排運用“交替式增長”模式，知識內容區間是有“脈絡”的，有前后的關聯也有縱橫交錯的聯系［3］.所以，培養學生的“讀、思、達”能力，就不能只著眼于本節課或本單元知識的“讀、思、達”，要從整套教材出發，把握知識點間的聯系，引領學生從“點”到“面”到“多維”的“讀、思、達”，引導學生反復“讀”，反復“思”，抓住知識間的聯系，實現對知識的重組和深度建構，從而培養學生的“讀思達”能力.

案例3“二次函數”復習課的教學片段

學生在學完“二次函數”這章后，基本上已經掌握了二次函數的概念、圖象及性質，所以，在復習課上可以通過設置一些相關的問題，引領學生“讀思達”.

第一環節：引達拋思引讀.

引達拋思：（1）什么是二次整式？寫出幾個關于x的二次整式.

（2）令你所寫的關于ｘ的二次整式為0，想想這是我們學過的什么內容？

（3）令ｙ等于你所寫的關于ｘ的二次整式，想想這又是我們學過的什么內容？

引讀：在學生回答完這三個問題后，教師引導學生再次回讀教材——①七年級上冊第87至88頁有關整式的內容；②九年級上冊第31至32頁有關一元二次方程的內容；③九年級下冊第29至30頁有關二次函數的內容和第51至52頁有關二次函數與一元二次方程的內容.

第二環節：引思引達再引思.

在學生讀完相關教材內容后，引導學生通過觀察對比思考：整式、一元二次方程、二次函數是有關聯的，有什么關聯？它們之間又有什么內在聯系？通過對這兩個問題的回答促進了學生對二次函數“面”的建構.

第三個環節：引達拋思.

在復習完二次函數圖象與性質后，提出：（4）令你所寫關于ｘ的二次整式大于或小于0，你們又有什么發現？學生通過對這個問題的理解和表達，可以感悟到整式、一元二次方程、二次函數和一元二次不等式之間的關系.然后提出：（5）雖然我們還沒有學習二次不等式的解法，但能否借助二次函數的圖象與性質來解決這個問題？先由學生思考，教師再引導學生根據二次函數的圖象及性質簡要地解答這個問題，實現了二次函數從“點”到“面”到“多維”的拓展，進一步提升了學生的“讀思達”能力.

愛因斯坦曾經說過：知識是會忘記的，留下來的是教育.掌握知識不是教育的最終目的，培養獲得知識的能力才是教育的最大目標［2］.所以，在“雙減”背景下，教師應當充分挖掘并運用教材資源，培養學生的“讀思達”能力，促進學生核心素養的形成和發展.

參考文獻：

[1]中華人民共和國教育部.義務教育數學課程標準[S].北京：北京師范大學出版社，2012.

[2]汪飛飛.從意義創生視角研讀數學教科書：何為、為何與可為——與新手數學教師的對話[J].中小學教師培訓，2019（8）：29-33.

[3]陶德軍.談北師大版初中數學教材的解讀[J].中小學教學研究，2013（6）：60-62.