對幾道經典幾何題輔助線生成的新思考

摘要：幾何題的輔助線生成常常有不同的解讀，有的是技巧性模式化操作，有的則是通性通法，闡明解決一類問題的思考方法．一般地，借助“知識溯源式目標分析法”從目標入手，通過追溯達成目標的基本途徑（即知識源），再結合條件選擇適當的解決問題的方法往往就是通性通法.從“教怎以想”入手，挖掘解題思路生成的通性通法，值得廣大同仁深入探討．

關鍵詞：輔助線生成；通性通法；知識溯源式目標分析法

不少經典幾何題都有較強的生命力，是課堂教學培養學生演繹推理能力的例題常青樹，深得廣大同仁的偏愛．不過，其中有些題輔助線的生成常常被錯誤解讀成模型化硬性操作，只是讓學生生搬硬套，卻忽略了從教“怎樣想”的角度引導學生學會思考，從而使得教學價值打了折扣．下面筆者隨意采擷四例，并從“怎么想到這樣做”解讀輔助線生成的必然性，以期拋磚引玉．

1 例題分析

1.1 輔助線的生成是圖形變換嗎？

例1在Rt△ABC中，∠C=90°，D為AB的中點，DE⊥DF，點E，F分別在邊AC，BC上．

求證：AE2+BF2=EF2．

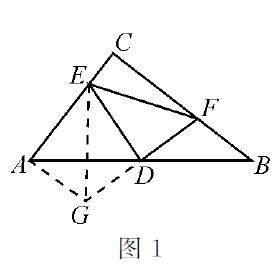
本題是一道經典的幾何題，如圖1，常規思路強調由D為AB的中點想到把△BDF旋轉180°至△ADG的位置，則∠CAG=∠CAB＋∠GAD=∠CAB+∠B=90°．連接EG，由“邊角邊”（DG=DF，∠EDG=∠EDF=90°和DE=DE）易證△EDG≌△EDF，得EG=EF，所以AE2+BF2= AE2+AG2=EG2=EF2．

當然，也有學生從倍長中線角度分析，強調由D為AB的中點想到延長FD至點G，連接AG和EG后仿上也可證得．

顯然，上述兩種解題思路都是指令性的，即看到中點就應該怎么操作，至于為什么這樣添輔助線卻沒有作深入剖析，不利于學生邏輯推理能力的形成與發展．其實，若借助“知識溯源式目標分析法”，從要證結論入手，不僅能闡明輔助線生成的必然性，還能引導學生學會“怎樣想”，進而提升他們分析問題的能力．

所謂“知識溯源式目標分析法”就是由要證結論AE2+BF2=EF2（目標）出發，追溯達成目標的相關知識源．而由目標的結構特征易想到該知識源就是勾股定理，可惜AE，BF和EF不在同一個直角三角形中，需等量轉化或重新構造直角三角形．因為AE是所構造的直角三角形的直角邊，所以想到過A點作AG⊥AE，且截取AG=BF，則問題轉化為證明EG=EF，即證明△EDG≌△EDF．考慮到∠EDF=90°和∠ADE+∠BDF=90°，所以想到證明∠ADG=∠BDF且DG=DF，即△ADG≌△BDF．由∠CAB+∠B=∠CAB+∠GAD=90°，可知∠GAD=∠B，依據“邊角邊”定理易知△ADG≌△BDF，問題得證．

由此可見，以AE，BF和EF為邊構造直角三角形才是圖1輔助線自然生成的本源，是通性通法.因為順延此思路，添出例2的輔助線就順理成章了．

例2在四邊形ABCD中，∠ABC=30°，∠ADC=60°，AD=CD．

求證：AB2+BC2=BD2．

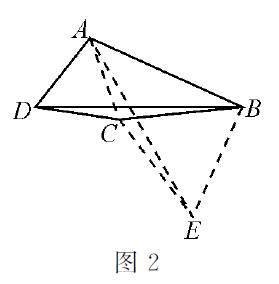
類比例1易想到需構造以AB，BC和BD為邊的直角三角形.如圖2，過點B作BE⊥AB，且使BE=BC，則問題轉化為證明AE=BD，而從兩線段的位置特征想到，適合用全等三角形對應邊相等來證明．為此需連接AC與CE，易證△ACD與△BCE均為等邊三角形，得CD=CA，CB=CE，∠ACD=∠BCE=60°，進而得∠DCB=∠ACE，故△DCB≌△ACE，問題得證．

事實上，對圖2輔助線的生成原本都是從旋轉角度加以解讀，即由等邊三角形ACD聯想到把△BCD繞點C按順時針方向旋轉60°得△ACE，然后再證明△ABE為直角三角形．當然此輔助線的作法也有一定的合理性，意在通過等量變換把三條線段轉化到同一三角形中，不過是一種試探性操作，難免有記憶性的模式化操作之嫌，沒有從輔助線生成本源上引導學生學會“怎樣想”，對思維能力的形成與發展意義不大．

總之，根據倍長（構造中心對稱圖形）和旋轉添加輔助線只是手段，是技巧，而構造直角三角形才是終極目標，是通性通法．

1.2 輔助線的生成是拼圖嗎？

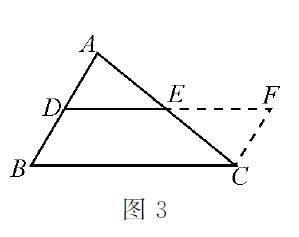
類似地，關于三角形中位線定理證明的輔助線生成，一般都是通過沿三角形中位線把原三角形剪開再拼成平行四邊形，從而啟發學生添出如圖3所示的輔助線．顯然這種鋪墊式添加輔助線的處理方式有牽著學生走之嫌（但也符合學生的認知基礎和認知規律），而借助“知識溯源式目標分析法”分析，不僅可挖掘輔助線生成的本源，還能引導學生學會“怎樣想”，從而完善思維方式．

若從證明目標DE∥BC出發，追溯之前學過的與證明兩線平行有關的知識源主要有“平行線的判定定理”“平行于同一條直線的兩條直線平行（傳遞性）”“平面內垂直于同一條直線的兩條直線平行” 和“平行四邊形對邊平行”.雖然從圖形特征易想到運用知識源“同位角相等（或同旁內角互補）兩直線平行”的判定定理，可惜要證明∠ADE=∠ABC需用到還未學習的定理“相似三角形對應角相等”，且又缺少第三條平行線與垂線，所以只好選擇知識源“平行四邊形對邊平行”加以證明，即過點C作CF∥AB，交DE的延長線于點F（證明略）．

若從要證目標DE=12BC入手，自然想到知識源“線段中點的意義”“直角三角形中30°角所對的直角邊等于斜邊的一半”和“直角三角形斜邊上的中線等于斜邊的一半”（在學習三角形中位線之前只有這三個），但題中缺少直角三角形要素，所以宜選擇第一個知識源處理，即延長DE至點F，使EF=DE，則問題轉化為證明DF=BC，故而也是證明四邊形DBCF為平行四邊形．

由此可見，構造平行四邊形才是證明三角形中位線定理輔助線生成的本源，是通性通法，而拼圖只是手段．

1.3 輔助線的生成是作高嗎？

例3如圖4，在銳角三角形ABC中，BE，CF是邊AC，AB上的高，在射線BE，CF上，分別截取BQ=AC，CP=BA．再過點P，Q分別作PM⊥BC，QN⊥BC，垂足分別為M，N．

求證：PM+QN=BC．

本題的輔助線是過點A作AG⊥BC，垂足為G，如圖5，然后分別證明△ABG≌△CPM，△ACG≌△BQN，得BG=PM，CG=QN．至于怎么想到這樣作輔助線的，一般解讀為由高BE與CF想到作△ABC的第三條高AG（或由垂直比較多的情況下想到作垂線）．這種解釋難免牽強，若從要證目標著手分析，則由三條線段間的數量關系想到通性通法——“截長”與“補短”．

若采用“截長”，不妨在邊BC上截取BG=PM，則問題轉化為證明CG=QN.而由這兩條線段的位置關系易聯想到連接AG，利用全等三角形對應邊相等加以證明．顯然△BQN與△ACG已經滿足BQ=AC和∠Q=∠ACG（∠Q+∠QBN=90°和∠ACG+∠CBE=90°），還需證明另一對對應角相等．注意到∠QNB=90°，所以需證明∠AGC=∠AGB=90°，即證明△ABG≌△CPM．由∠PCM+∠CPM=90°和∠CBF+∠PCM=90°，得∠CPM=∠ABG，由“邊角邊”定理易證兩三角形全等，問題迎刃而解．

若考慮“補短”，不妨延長QN至點H，使QH=CB（如圖6），連接BH，則問題轉化為證明HN=PM．由輔助線的添法和前文作高AG的證法，易證明△BQH≌△ACB（SAS），得BH=AB=CP，∠H=∠ABC=∠CPM.根據“角角邊”可證△BNH≌△CMP，則PM=HN，問題又迎刃而解．

由此可見，作高只是輔助線生成的表象，“截長補短”才是處理三條線段間數量關系類問題之本，是通性通法．當然，對于輔助線生成后究竟如何表述則不拘一格，化繁求簡（如圖5就可表述成“作BC邊上的高”，以求簡化證明過程）．由此出發，添出例4的輔助線也就是手到擒來之舉了．

例4如圖7，在四邊形ABCD中，AB=AD，∠B+∠ADC=180°，E，F分別是邊BC，CD延長線上的點，且∠EAF=12∠BAD．求證：BE-DF=EF．

顯然BE是三條線段中最長的線段，圖8從補短角度入手，延長DF至點G，使DG=BE（如圖8），則問題轉化為證明GF=EF.連接AG，即證明△AGF≌△AEF．根據同角的補角相等，可得∠B=∠ADG.由“邊角邊”定理得△ABE≌△ADG，所以AE=AG且∠BAE=∠DAG，則∠EAG=∠BAD，進而得∠EAF=∠GAF，再依據“邊角邊”定理可證△AGF≌△AEF，結論得證．當然也可在BE上截取BM=DF（截長），連接AM，通過證明△AEM≌△AEF而得結論正確（圖略）．

另外，不少同仁把例4歸納為半角模型，強調旋轉的模式化操作（即把△ABE繞點A旋轉至△ADG的位置），這顯然有未能透過現象看清本質之嫌．

2 兩點感悟

2.1 解題研究要著力于通性通法

毋庸諱言，模型化操作雖然給學生解題提供了可套用的模型，在一定程度上提升了解題速度，但這畢竟是技巧性操作，不僅應用范圍有一定的局限性，而且只是教“怎樣做”，學生并沒有學會“怎樣想”，沒有真正形成分析能力，一旦遇到無模可套的問題便又陷入束手無策的窘境．相反，加強解題通性通法生成過程的研究卻能從根本上豐富學生解題的思維方式，打通分析問題的思維通道，發展調控受阻思維的能力，從而學會分析．當然研究通性通法一定要堅持從目標入手分析（如例1、例2中兩條線段的平方和等于第三條線段的平方），挖掘解題思路生成的知識源，探求處理問題的基本策略（如例1、例2以目標中的三條線段為邊構造直角三角形），優化調控策略（如對于例3圖5中的補短法，輔助線若表述成“延長QN至點H且使NH=PM”，則給證明制造了不小的障礙；但描述為“延長QN至點H且使QH=BC”，則解題思路豁然開朗）．

2.2 解題研究要追求“以題會類”

眾所周知，“以題會類”是習題教學的最高境界.但要真正實現“以題會類”，除了加強通性通法的研究外，還可開展基于知識源配套習題專題整理活動，以提升學生同類題型的系統梳理能力，明確解題的思考方向和思路生成的本源，全面掌握處理同類問題的基本策略，切實提升分析問題的能力．如，在中考復習時可就“線段中點定義”“直角三角形中30°角所對的直角邊等于斜邊的一半”“直角三角形斜邊上的中線等于斜邊的一半”“三角形的中位線等于第三邊的一半”“三角形的重心分中線之比為1∶2”和“直接求兩線段長計算證明”等“線段二倍關系”的知識源，配備相應例題（限于篇幅，例題從略，感興趣的讀者不妨參閱文獻[1]），提升學生處理同類問題的能力，追求“以題會類”的習題教學最高境界．

總之，習題教學是數學課堂教學鞏固知識和提升能力的重要環節，而借助“知識溯源式目標分析法”，從“教怎樣想”入手，挖掘解題的通性通法，或許是提升學生分析問題能力的有效舉措.當然，如何加強習題教學研究是個“仁者見仁智者見智”的永恒課題，單就“如何研究”和“研究什么”就值得廣大同仁深入探討．

參考文獻：

[1]劉華為．通過“溯源”學會“怎樣想”[J].中學生數學，2019（2）：2-4.