單級齒輪傳動系統非線性動力學分析

蔣強

關鍵詞：機械振動;非線性動力學;齒輪傳動系統

中圖分類號：TH132.413;O32 文獻標志碼：A

0引言

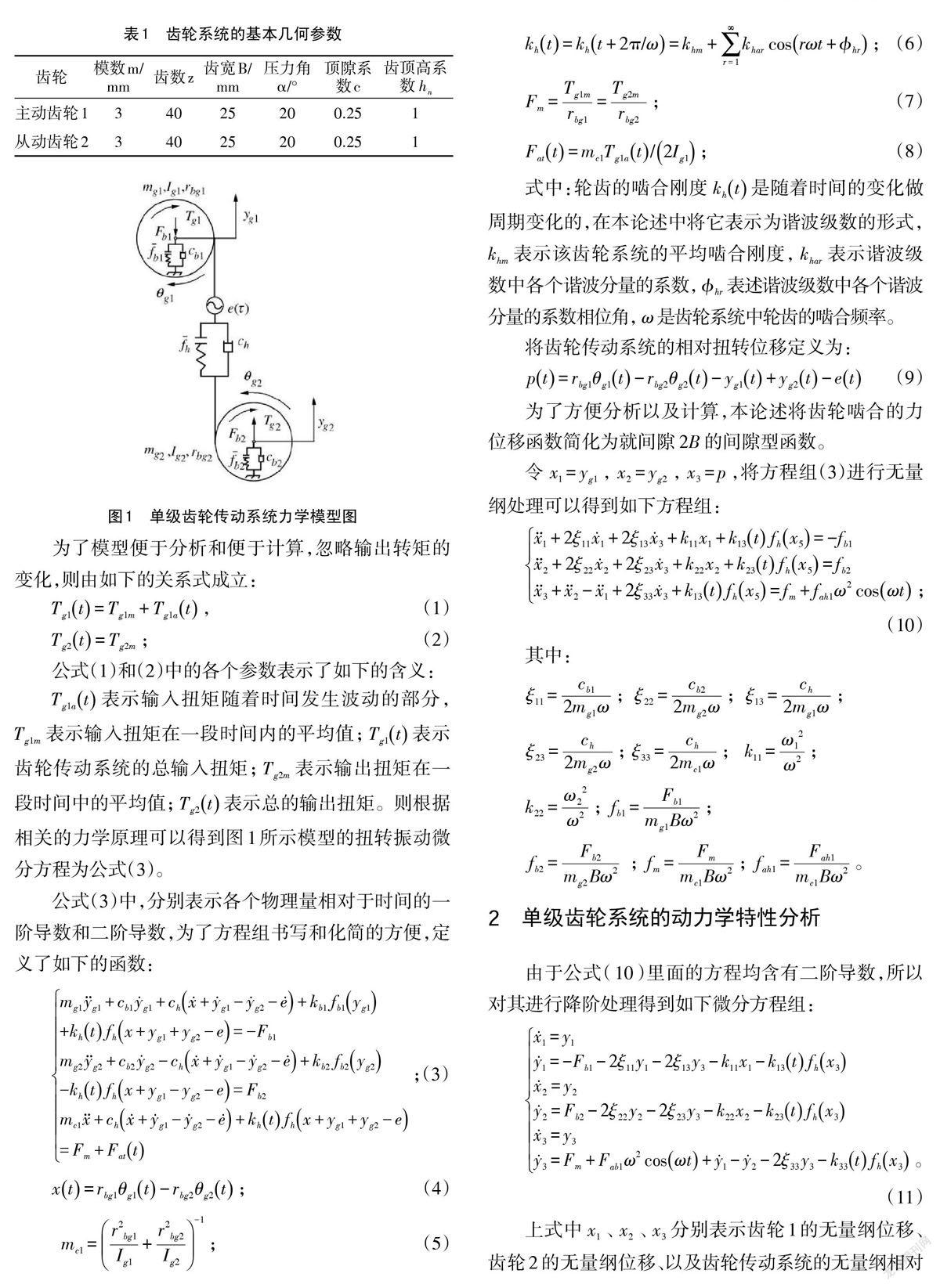
合肥工業大學盧劍偉[1]教授考慮了參數隨機激勵對齒輪系統動力學的影響，選擇用蒙特卡羅法對兩自由度齒輪傳動系統分析，得出了系統的動態特性隨參數隨機擾動的變化情況。胡鵬[2]等選擇直齒齒輪系統建立了純扭動力學模型，分別分析了嚙合剛度、轉速、動態傳遞誤差不同時模型動力學特性的變化趨勢。林騰蛟[3]與王三民[4]教授以綜合考慮剛度激勵、誤差激勵以及嚙合沖擊激勵的弧齒錐齒輪傳動系統為對象，通過分析得到了錐齒輪傳動系統內部激勵的變化曲線。西北工業大學王三民[4]教授又考慮了齒側間隙和時變嚙合剛度，通過分析發現當選取嚙合頻率作為分岔參數時，系統通過倍周期分岔形成混沌;而選取支承剛度作為分岔參數時，齒輪系統通過擬周期分岔振動形成混沌振動。中南大學教授唐進元[5-6]專門針對時變阻尼項和剛度項之間的耦合作用使周期解的平均值發生漂移這一現象提出了改進方法—能量迭代法，并推導出了系統主振動的幅頻響應方程和相頻響應方程。本論述通過對三自由度單級直齒齒輪傳動系統進行受力分析，建立了運動微分方程組并進行數值仿真，通過單級齒輪傳動系統隨著嚙合頻率變化的全局分岔圖、相圖和龐佳萊截面圖進行研究。

其中D表示無量綱以后的間隙。

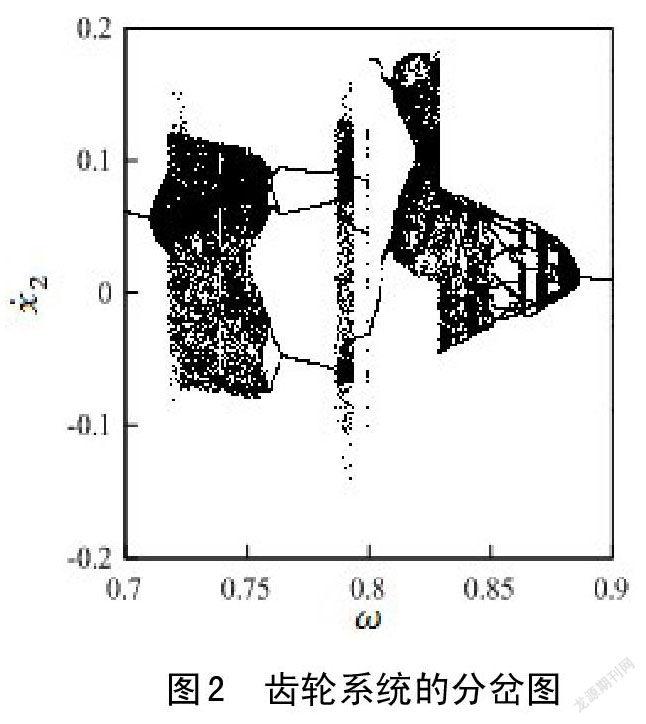
假設齒輪1、齒輪2的速度和位移以及相對扭轉位移和相對扭轉速度均為0，則頻率ω在區間[0.7，0.9]內變化時齒輪2速度的分岔圖、相圖和龐佳萊截面圖分別如圖2和圖3所示。當轉矩波動頻率ω<0.7105時，齒輪系統的運動狀態表現為穩定的周期1運動，此狀態下系統的相圖和龐佳萊截面圖如圖3（a）所示;隨著轉矩波動頻率ω 的增大，當ω=0.7105時，齒輪系統發生了Hopf分岔，系統的運動狀態突變為概周期運動，系統的相圖變為無數個封閉的曲線環，龐佳萊截面圖由一個穩定的不動點突變為一個極限環;隨著頻率的繼續增大，極限環發生了環面倍化，轉矩波動頻率繼續增大到ω=0.7178時，系統的運動狀態再一次發生突變，極限環破裂，系統的運動狀態也突變為了混沌運動;此時系統的混沌運動一直持續到ω=0.7381，在ω=0.7381這一點系統的運動狀態又突變為周期運動，此時周期運動的相圖和龐佳萊截面圖如圖3（c）所示;周期運動所持續的頻率范圍并不大，當頻率繼續增大到ω=0.7395時系統的運動狀態又一次突變為混沌運動;當頻率繼續增大到ω=0.7587時，系統的運動狀態由原來的混動運動經逆Hopf分岔突變為周期運動，在圖3中給出了周期6運動的相圖和龐佳萊截面圖如圖3（d）所示。

緊接著又給出了系統隨支撐剛度和嚙合阻尼的全局分岔圖，如圖4和圖5所示;通過對比圖4各圖可以知道：當其它參數在給定值下保持不變時，隨著主動軸支撐剛度k和從動軸支撐剛度k的同時增大，系統混沌運動的區域在逐漸減小。即隨著嚙合阻尼的逐漸增大，系統的運動狀態變得愈加穩定，因此為了保證系統可以穩定的運動，支撐剛度應該取較大的值。通過對比圖5各圖可以知道：當其它參數在給定值下保持不變時，隨著嚙合阻尼ξ的增大，系統剛開始周期運動的曲線和結束時的周期曲線均在逐漸變長，系統混沌運動的區域在逐漸減小。即隨著嚙合阻尼的逐漸增大，系統的運動狀態變得愈加穩定，因此為了保證系統可以穩定的運動，嚙合阻尼應該取較大值。

3 總結

（1）本論述采用了集中參數法來建立三自由度單級直齒齒輪傳動系統的模型，對單級齒輪嚙合系統進行了受力分析，并進行無量綱化處理，利用龍格庫塔法進行數值求解，得到齒輪系統在不同轉矩波動頻率、支撐剛度下系統的分岔圖、相圖以及poincaré映射圖。

（2）隨著頻率的增大，從動輪的運動狀態中包含了周期運動、概周期運動、混沌運動等;通向混沌的道路有周期倍化、Hopf分岔、橢圓面破裂等。

（3）最后分析了嚙合阻尼和支撐剛度對齒輪系統運動的影響，通過對比得到為了系統可以穩定的運行，嚙合阻尼和支撐剛度均應該選取比較大的值。