非二次條件下一類橢圓系統的正解

吉 蕾

(晉中學院 數學系，山西 晉中 030619)

0 引言

考慮如下一類橢圓系統

(1)

其中：Ω?RN(N≥5)是具有光滑邊界?Ω的有界開集，參數k≥0.

系統(1)源自文獻[1]建立的數學模型.自此，四階橢圓型方程得到了人們廣泛的關注研究，近期相關結果可參見文獻[2-6]等及其相關文獻.文獻[7]研究了系統(1)在一維情形下解的存在性.在非線性項形式更一般時，文獻[8]運用山路引理和強極大值原理得到了系統(1)的正解.山路引理的運用需要假設(AR)條件，但在實際應用中，有很多函數不滿足(AR)條件.文獻[9]中作者提出了非二次條件.因此，本文考慮了非二次條件下系統(1)正解的存在性.

1 預備知識

下面給出本文所用的一些符號和定義，以及用到的命題.

設λ1是問題

-Δu=λu，x∈Ω，u=0，x∈?Ω

Δ2u=λu，x∈Ω，Δu=u=0，x∈?Ω

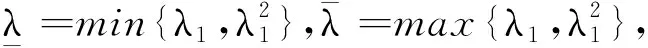
由變分法知，系統(1)的弱解對應于以下能量泛函的臨界點：

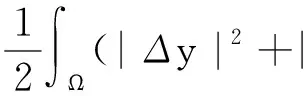
其中：u=(y,z)∈V；F(x,u)為系統(1)的位勢函數，即

?uF(x,u)=f(x,u)=(f1(x,u),f2(x,u)).

且對?u=(y,z)，v=(ξ,η)∈V，

下面給出泛函J滿足(C)c條件的定義及證明中用到的環繞定理：

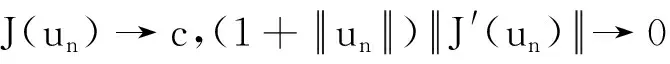
環繞定理[11]設H是實Hilbert空間，泛函J∈C1(H,R)，對?c>0，滿足(C)c條件.若存在閉子集S?H和Hilbert流形Q?H，且滿足：

(ii)S與?Q環繞；

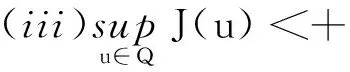
則泛函J有臨界值c≥β.

2 主要結果

定理1假設系統(1)滿足條件(H1)-(H5)：

(H1)f1，f2∈C(Ω×R2,R).當x∈Ω，u=(y,z)∈R2時，f1(x,u)，f2(x,u)≥0.

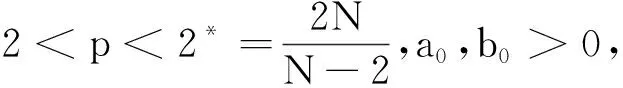
|f1(x,u)|+|f2(x,u)|≤a0|u|p-1+b0.

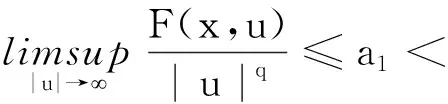
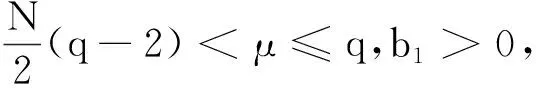
(H5)存在a2，b2>0，使得

關于a.e.x∈Ω一致成立.

則系統(1)至少有一個正解.

推論假設(H1)～(H4)成立，且

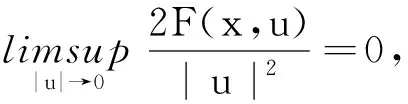
關于a.e.x∈Ω一致成立，則系統(1)至少有一個正解.

注定理中的條件(H4)即為非二次條件.比較上述結果和文獻[8]中的定理，文獻[8]中的條件(H3)即為(AR)條件，容易找到滿足推論條件而不滿足(AR)條件的函數，例如

F(x,u)=|u|2ln(1+|u|2).

3 主要結果的證明

分三步完成定理的證明.

第一步 證明對?c∈R，泛函J滿足(C)c條件.

由條件(H2)，上述泛函J∈C1(V,R)，設c∈R，任取{un=(yn,zn)}?V且

(2)

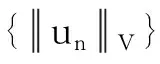
由(2)可得，存在M>0，使得

(3)

又由條件(H4)，存在實數M1>0，當|u|≥M1時，有

(4)

當|u|0，使得

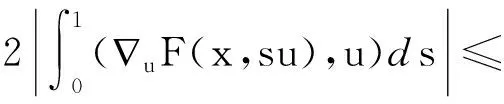
(5)

由(4)、(5)可知存在常數C2>0，使得對?u∈R2和a.e.x∈Ω，有

成立.因此由(3)可推知

(6)

由條件(H3)，存在常數M2>0，使得當|u|≥M2時，有

當|u|0，使得F(x,u)≤C4.對?u∈R2和a.e.x∈Ω，有

F(x,u)≤2a1|u|q+C4.

(7)

一方面，由(3)和(7)可得

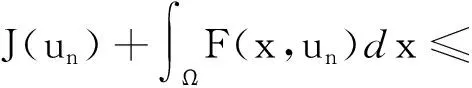
(8)

另一方面，當k≥0時，

(9)

因此由(8)、(9)可得

(10)

于是，將H?lder不等式、Sobolev嵌入不等式和式(6)應用于式(10)，可得

(11)

其中C6>0為常數.

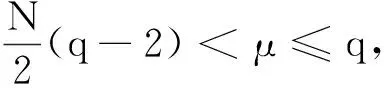
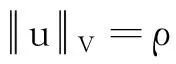
事實上，令

則

對ε0>0，由(H2)和(H5)可知，存在A≥0，B≥0，使得對?u∈R2和a.e.x∈Ω，

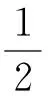
(12)

成立.所以

其中

又由(12)有

所以

(13)

令u0=(φ1,φ1)，則

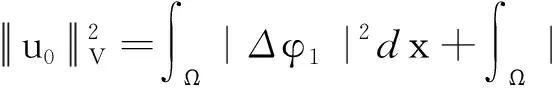
(14)

由(13)和(14)可得，當t→∞時，

第三步 證明泛函J存在非零臨界點，并證明該非零臨界點為系統(1)的正解.

應用環繞定理，令

其中t0>0，使得J(t0u0)≤0.因此泛函J存在臨界值c≥γ>0，設J(u*)=c>0，則J′(u*)=0，即u*為泛函J的非零臨界點，即為系統(1)在V中的非零弱解.設u*=(y*,z*)，根據(H1)可斷言：y*≥0且z*≥0.

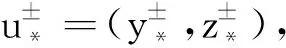
由k≥0得

由定理的結論，很容易推得推論成立.

4 結語

本文通過環繞定理和強極大值原理，當非線性項在無窮遠處滿足非二次條件時，得到了橢圓系統(1)正解的存在性. 此時非線性項更具一般性，所得結論推廣了相關文獻的內容.