彈性地基圓形加肋板靜力彎曲及彎曲自由振動分析的無網格法
彭林欣, 諶亞菁, 覃 霞, 楊健生
(1.廣西大學 土木建筑工程學院,南寧 530004; 2.廣西大學 廣西防災減災與工程安全重點實驗室,南寧 530004; 3.廣西大學 工程防災與結構安全教育部重點實驗室,南寧 530004)
加肋板因其剛度高、重量低的特點,被廣泛應用于房屋建筑、橋梁、船舶、航空及航天等工程領域,常見于地基板、路面板、機場跑道、船舶壁板等部位。因此,針對加肋板結構力學性能的研究受到了學者和工程技術人員的高度重視。一些特殊建(構)筑物,如水塔、煙囪、筒倉等,基礎形式大多采用加肋多邊形板或圓板,設計荷載較小時也可采用不加肋的形式。對于不加肋的平板式基礎,一般取彈性地基上的圓板作為力學模型。國內外學者對彈性地基上圓板計算分析開展了深入研究,如王超剛[1]利用Ritz法研究了中心受集中力作用的自由放置在彈性地基上圓板的彎曲問題,并獲得了該問題的解答。Wang等[2-4]通過引入非軸對稱屈曲模態正確計算了彈性地基圓板的屈曲荷載,并進一步研究了彈性地基上同心鉸接或帶裂紋圓板的屈曲問題。何芳社等[5]將與板相關的各力學量展開為Fourier-Bessel級數,利用解析法對彈性圓板下橫觀各向同性彈性地基的軸對稱問題進行了分析。Starovoitov等[6-7]研究了彈性地基上層合圓板在突發局部荷載作用下的軸對稱振動問題及周期荷載作用下的共振問題。裴昭等[8]研究了橫向軌跡動載作用下彈性基礎上各向同性圓薄板在彈性約束下的動力響應問題。
除了彈性地基上的平板外,國內外學者對彈性地基加肋板亦進行了大量研究。金康寧等[9-10]用邊界元法處理彈性地基上的薄板,用有限元法處理加肋板上的肋梁,利用肋梁結點處力的平衡和位移的協調關系進行耦合求解。蔡健等[11]將彈性地基上的加肋板視為十字交叉梁與平板的組合體系,通過梁、板、地基三者之間的力與位移平衡和協調分析,得出了梁板式筏基與地基共同作用的半解析解。Lee等[12-13]基于Mindlin板理論,采用有限元法分析了彈性地基上加肋板的動力特性。對于加肋板而言,采用有限元法進行分析時需要肋條沿板網格線布置。當肋條位置改變時,板的單元也要重新劃分以保證肋條與網格線的重合。
無網格法[14-15]是近年來興起的一種數值分析方法。不同于有限元法,無網格法的近似函數是建立在一系列離散點上的,不需要借助于網格,克服了有限元法對網格的依賴性。有限元線性單元的直邊不能承受彎曲荷載,分析過程可能會出現剪切閉鎖,無網格法沒有單元概念,可以有效避免剪切閉鎖。在涉及網格畸變、網格移動等問題中無網格法顯示出明顯的優勢,容易進行自適應分析,因而被廣泛應用于碰撞、動態裂紋擴展、金屬加工成型、流體力學以及其它領域中[16]。不少研究者已成功應用無網格法對加肋板進行分析,例如Liew等[17]采用基于一階剪切變形理論的無網格伽遼金法研究加肋折板在不同載荷和邊界條件下的彈性彎曲行為;Tamijani等[18-19]采用無網格伽遼金法分析了曲線加肋板及功能梯度板的自由振動;Sadamoto等[20-21]提出了一種有效的伽遼金無網格扁殼公式用于分析加肋板結構的彎曲問題;彭林欣[22-23]在一階剪切變形理論的基礎上建立了矩形加肋板的無網格模型,并研究了加肋板的彎曲和振動等問題。
目前采用無網格法對地基板的研究較少,大多集中在對板殼結構自身力學性能的分析[24-29],而考慮地基作用的不多。對于此類問題的分析主要有:熊淵博等[30-31]用無網格局部Petrov-Galerkin(MLPG)方法分析了Winkler彈性地基上正交各向異性板的彎曲問題。夏平等[32-34]采用無網格局部徑向點插值方法(LRPIM)研究了雙參數彈性地基中厚板的靜力彎曲問題。Shams等[35]用再生核質點法(RKPM)研究了Winkler-Pasternak彈性地基上碳納米管增強復合材料層合板在面內載荷作用下的屈曲行為。覃霞等[36-39]利用無網格法分析了彈性地基上矩形加肋板以及斜肋板的振動特性,并對彈性地基加肋板肋梁進行優化分析。對于彈性地基圓板,曾祥勇等[40]基于Mindlin中厚板理論,建立了Winkler 地基上圓形厚板彎曲撓度的無單元伽遼金法(element-free Galerkin method, EFGM)求解控制方程;肖勇剛等[41]基于EFGM分析了集中載荷作用下彈性地基圓板的彎曲問題。
綜上所述,鮮見文獻采用無網格法研究彈性地基加肋板線性彎曲的靜力和振動問題,特別是對圓形加肋板。本文利用無網格法的優勢,基于一階剪切理論和移動最小二乘法(moving least squares, MLS),提出分析彈性地基圓形加肋板線性彎曲的靜力和自由振動問題的無網格伽遼金法。首先,采用一系列離散點建立彈性地基圓形加肋板的力學模型,并通過肋條與平板的位移協調條件導出兩者節點參數轉換方程;其次,分別通過最小勢能原理和哈密頓原理建立靜力彎曲和彎曲振動的控制方程;最后,采用完全轉換法處理邊界條件。文中以不同幾何尺寸、材料參數、荷載分布、肋條布置形式的彈性地基圓形加肋板為例,將本文解與ABAQUS有限元解及文獻結果進行比較分析,并研究了影響域及離散節點個數對計算結果的影響。研究表明,該方法能有效地分析彈性地基圓形加肋板線性彎曲的靜力及自由振動問題,且具有計算穩定性好、結果易于收斂等優點。
1 彈性地基圓形加肋板彎曲的靜力與自由振動的無網格列式
無網格法采用點來離散計算模型,避免了單元的劃分。由此,本文基于無網格伽遼金法提出圓形彈性地基加肋板的無網格模型,計算其線性彎曲的靜力及自由振動問題。
1.1 彈性地基加肋板的無網格模型
一彈性地基圓形板如圖1所示,其中R、hp、hs和ts分別為圓板平板半徑、板厚、肋條高和肋條寬,λ為彈性地基系數。在本研究中,圓形平板和肋條為均質材料,彈性模量和泊松比分別記為E、μ。圓形加肋板為圓形平板與肋條的組合結構,兩者在交接處位移協調。彈性地基采用Winkler地基模型,以彈性模擬。本文基于無網格法,分別采用一系列點來離散圓形平板和肋條,平板節點數記為n,肋條節點數為m,平板與肋條采用獨立坐標系,具體如圖2所示。
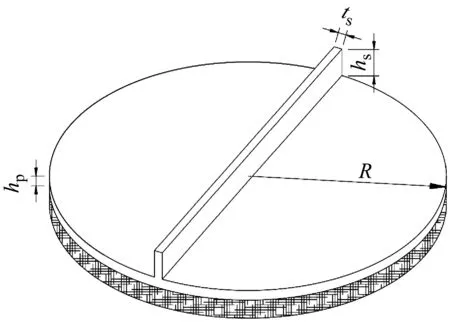
圖1 彈性地基上的圓形加肋板
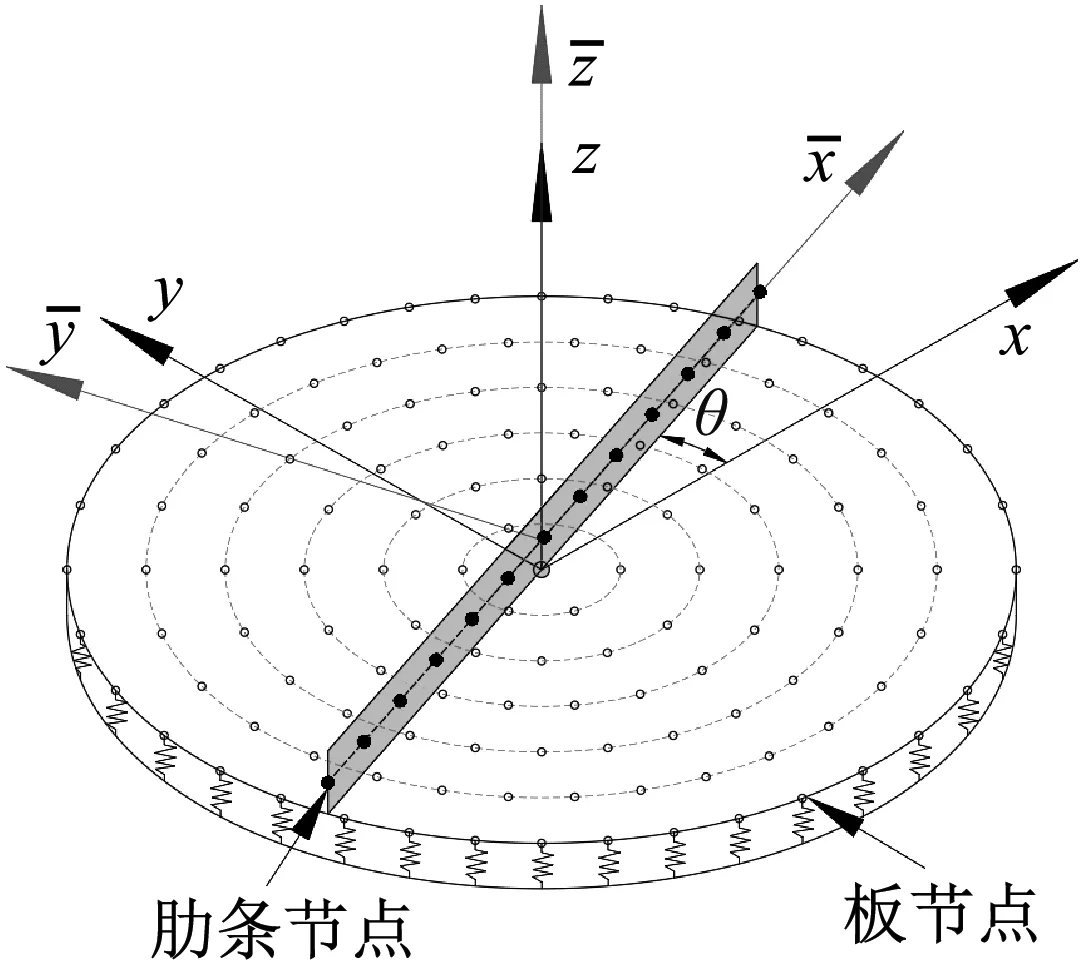
圖2 彈性地基上圓形加肋板的無網格模型
1.2 圓形平板和肋條的位移場
圓形平板包含5個自由度up、vp、p、φpx和φpy,其中前3個分別為沿著x、y、z軸的平動位移,后兩者分別為繞著y、x軸的轉角。采用移動最小二乘法[42]建立形函數,根據一階剪切理論[43],圓形平板的位移場可近似為
(1)
用矩陣形式
(2)
式中:[u0pI,v0pI,pI,φpxI,φpyI]T=ΔpI為圓形平板節點參數;φpx、φpy與p完全獨立。
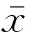
(3)
或寫成矩陣形式
(4)
式中:[u0sI,sI,φsI]T=ΔsI為肋條節點參數;φsI與sI完全獨立。
1.3 圓形平板與肋條的位移協調方程
如圖3所示,肋條任一點S,必定在平板上存在對應點P(在整體坐標系xyz中,P與S的xy坐標相同,P可以是板上任意點,不一定屬于板上的離散點),C點為P、S兩點連線與板面的交點。對于同心肋條三點重合。根據C點的位移協調條件,有:
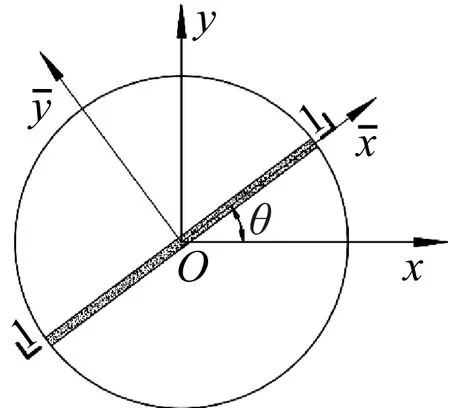
圖3 位移協調示意圖
p=s
(5)
φpxcosθ+φpysinθ=φs
(6)
upcosθ+vpsinθ=us
(7)
由式(5),(6)和(7),可得
(8)
(i=1,…,m)
(9)
(10)
根據移動最小二乘法,式(5),(6)和(7)可寫成
(11)
(12)
(13)
將式(11),(12)和(13)寫成矩陣形式
TpΔp=TsΔs
(14)
其中:
Δp=[u0p1v0p1p1φpx1φpy1u0p2v0p2p2φpx2φpy2…u0pnv0pnpnφpxnφpyn]T,
Δs=[u0s1s1φs1u0s2s2φs2…u0smsmφsm]T,
由式(14)可推出
Δs=TspΔp
(15)
其中:
(16)
對式(15)關于時間求導可得
(17)
綜上所述,通過肋條與平板的位移協調條件可將肋條節點參數轉換成板節點參數,轉換方程為式(15)。當肋條位置改變時,只引起矩陣Tsp的改變,因此只需要重新計算該矩陣。
1.4 圓形加肋板與彈性地基的接觸勢能
假定彈性地基與圓形加肋板緊密接觸,則兩者的位移滿足連續條件。設基床反力系數為λ,則接觸力勢能可表示為
(18)

1.5 彈性地基圓形加肋板彎曲的自由振動控制方程
根據1.2節圓形平板的位移場,其面內應變可表示為
(19)
面外應變為
(20)
其中:
從而可以導出圓形平板的勢能
(21)
其中:
Δp=[Δp1Δp2…Δpn]T,
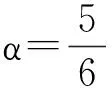
同樣,圓形平板的動能為
(22)
式中:
對于肋條,其應變表示為
(23)
(24)
式中:
從而可導出肋條的勢能
(25)
式中:
Δs=[Δs1Δs2…Δsm]T,
As為肋條截面面積。同樣,肋條的動能表示為
(26)
式中:
疊加式(18)、(21)、(25),整個彈性地基圓形加肋板的勢能可表示為
(27)
疊加式(22)、(26),其總動能可表示為
(28)
由式(15)、(17)給出的轉換方程,整個圓形加肋板的勢能和動能可分別表示為
(29)
(30)
式中:
由Hamilton原理可導出結構的自由振動控制方程
(31)
進而結構的自振頻率由以下方程求出
(K-ω2M)Δp=0
(32)
1.6 彈性地基圓形加肋板的靜力彎曲控制方程
如圖4所示,一彈性地基圓形加肋板受面外荷載q(x,y)作用,該外力做的功為
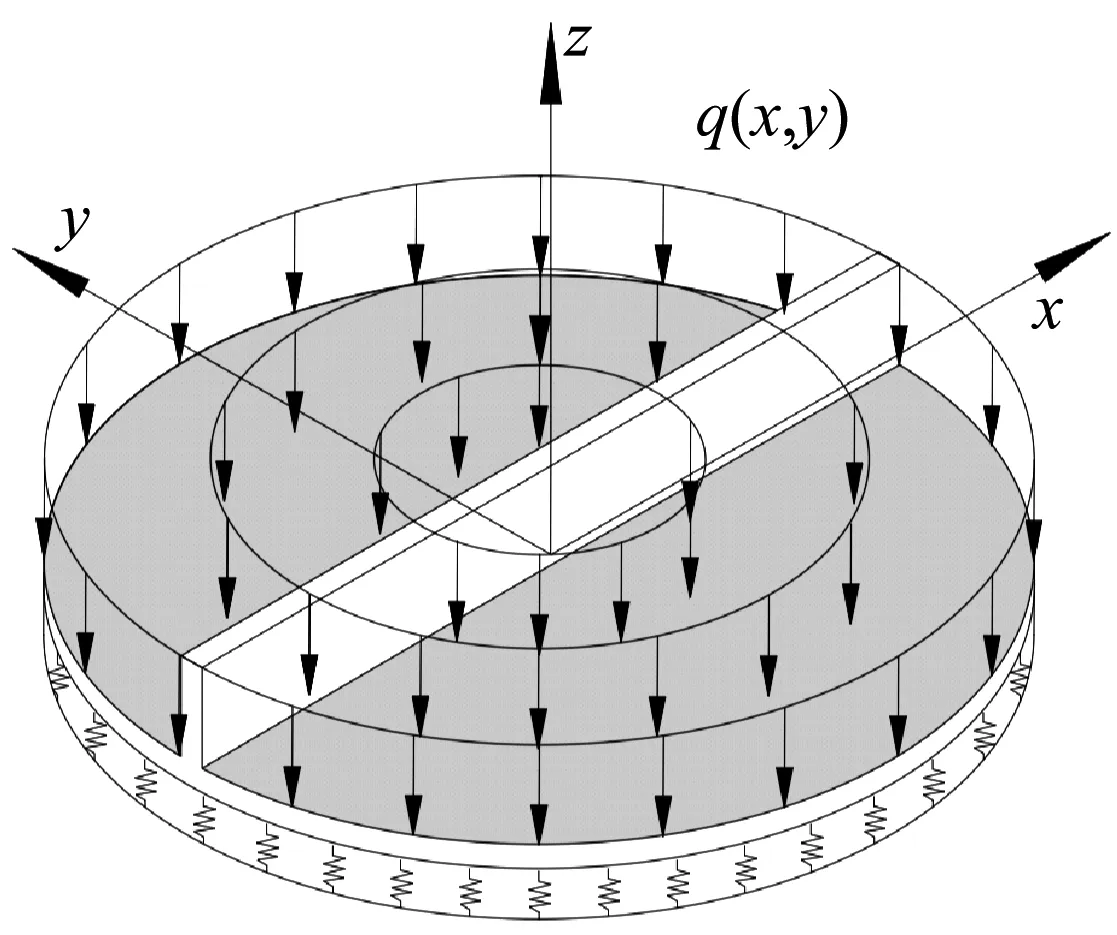
圖4 彈性地基圓形加肋板受面外荷載作用
=?q(x,y)pdxdy
(33)
根據MLS可寫成
(34)
其中:
疊加應變勢能和外力勢能(外力做功的相反數),有總勢能
(35)
由最小勢能原理δΠ=0可導出彈性地基圓形加肋板的靜力彎曲控制方程如下
KΔp=f
(36)
2 算例分析
2.1 收斂性分析
采用不同節點離散方案分析本文方法的收斂性。對一鉸接彈性地基單肋條圓形加肋板做自由振動分析。板與肋條材料相同,材料和幾何參數為E=17 MPa,μ=0.3,R=0.5 m,hs=0.1 m,hp、ts均為0.01 m,λ= 4.0×104N/m3,ρ=1 000 kg/m3。背景網格尺寸均為0.12 m×0.12 m。
2.1.1 節點離散方案
如圖5所示,為確定統一的節點離散方案,將圓板分成n個同心圓,每個圓有6n個節點,肋條有2n+1個節點。影響域擴大系數dmax定義為
其中:r是節點的支撐半徑;dmax表示影響域的大小。在本算例中,dmax取值為4.0。用不同的節點離散方案獲得的前4階自振頻率如表1所示。其收斂曲線如圖6所示。研究表明,當n大于6時,計算結果趨于穩定,可認為該節點離散方案使計算收斂。
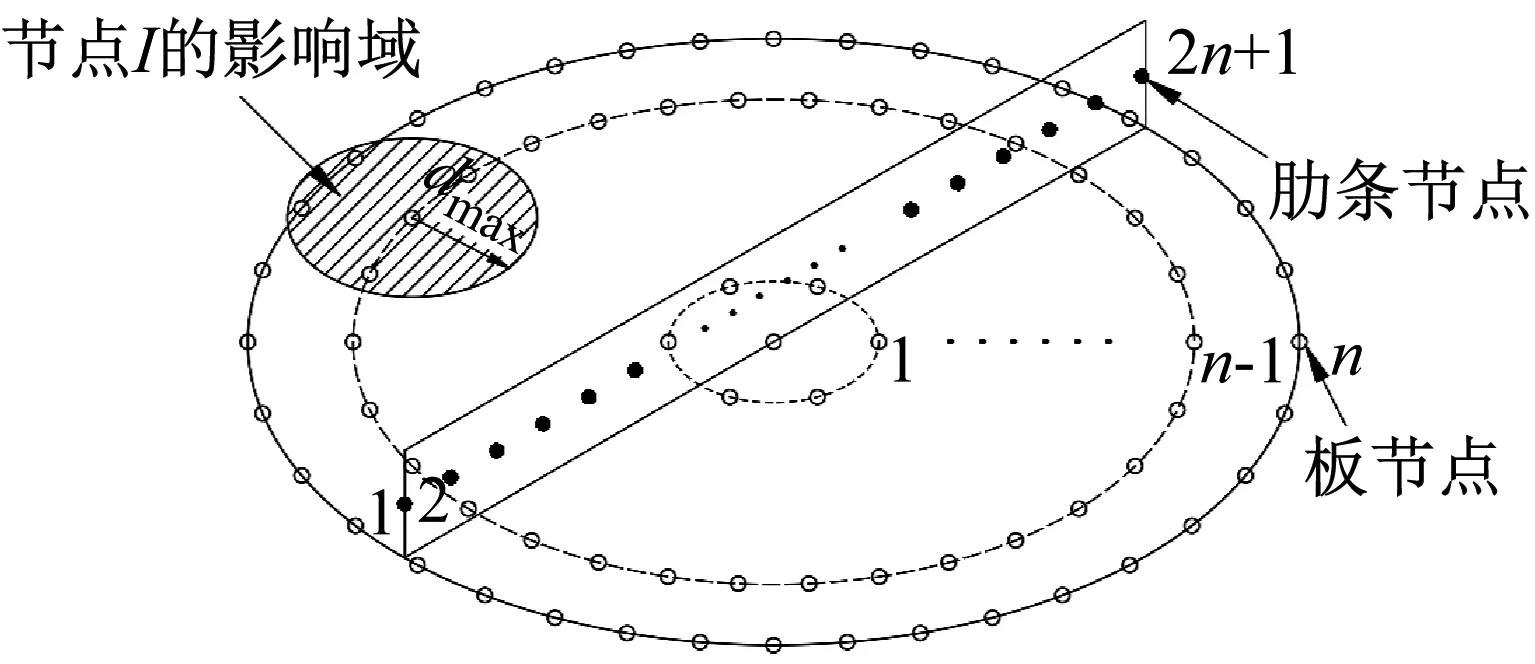
圖5 圓形加肋板的節點離散方案
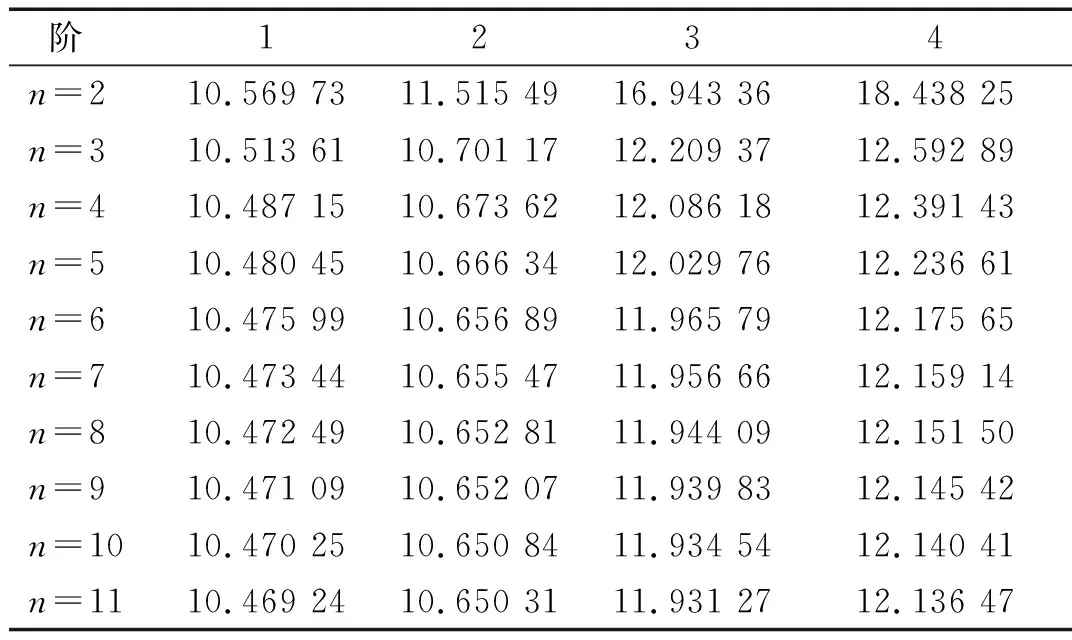
表1 不同節點離散方案下彈性地基單肋條圓板的頻率
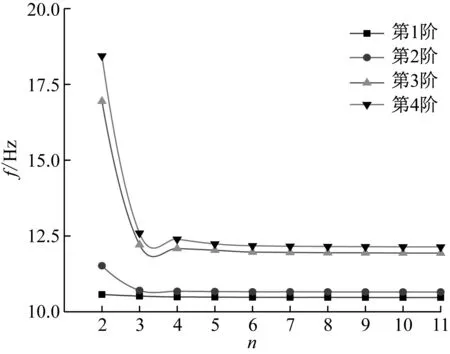
圖6 不同節點離散方案下彈性地基單肋條圓板頻率隨離散階數的變化
2.1.2 影響域
在本算例中,圓板用169個節點離散,肋條用15個節點離散,即n為7。在不同dmax下獲得的自振頻率如表2所示。前4階自振頻率隨dmax的增加而變化的趨勢如圖7所示。研究表明, 當dmax的取值大于3.0時,計算趨于穩定。
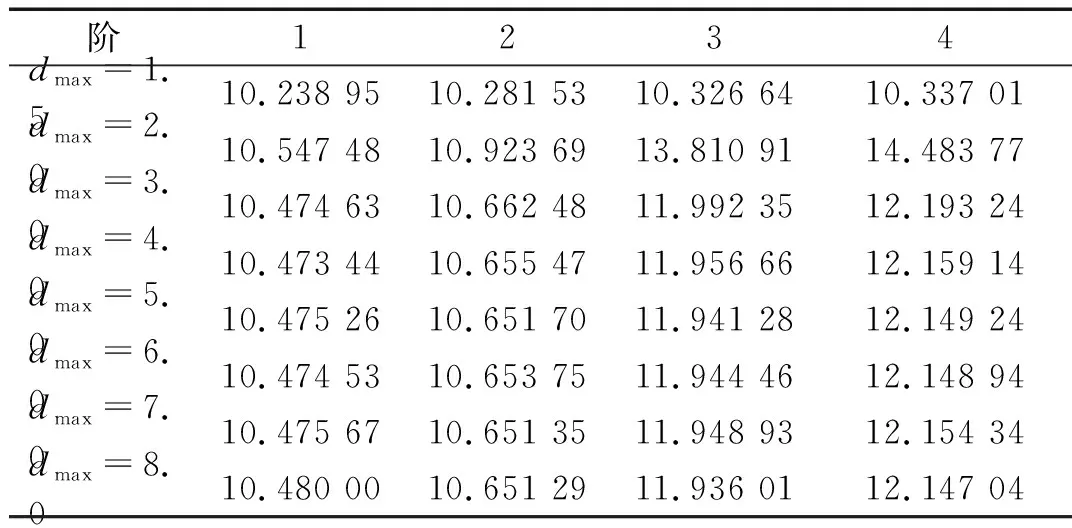
表2 不同dmax下的彈性地基單肋條圓板頻率
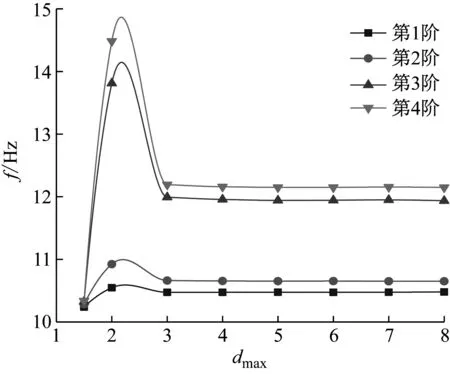
圖7 彈性地基單肋條圓板在不同dmax下的頻率
通過對算例分析可知,本文方法收斂性好。當圓板采用169個節點規則離散(即n=7)及dmax的取值在3.0~6.0之間的節點離散方案可給出滿意的計算結果。
2.2 有效性分析
采用上述無網格方法對彈性地基圓板進行自由振動分析。一彈性地基上的自由圓板的幾何和物理參數為:半徑R=1.0 m,板厚hs=0.1 m,彈性模量E=1.166 7×1010Pa,泊松比μ=0.166 7,密度ρ=2 460 kg/m3,基床系數λ=1.0×107N/m3。將本文方法計算得到的自振頻率與文獻[44]進行對比,結果如表3所示。
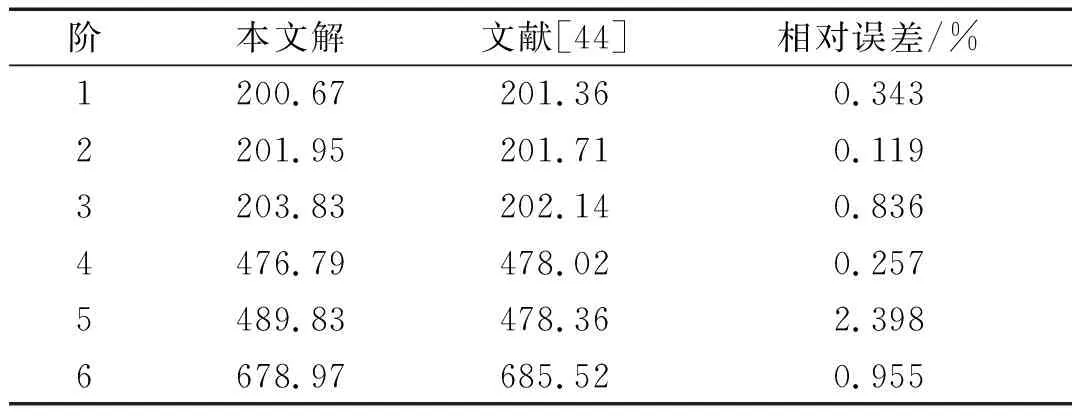
表3 彈性地基上的自由圓板的頻率
采用上述無網格方法對彈性地基圓板進行靜力彎曲分析。彈性地基上圓板作用一軸對稱圓形均布荷載,荷載作用半徑為0.18 m,均布力集度q為1 000 kN/m2,λ=5×104kN/m3,E=2.45×107kN/m3,μ=1/6,圓板半徑為1.35 m,板厚hs為0.25 m。將本文方法計算得到的撓度與文獻[45]的結果進行對比,如表4所示。

表4 彈性地基圓板受載的靜力撓度
結果表明,本文解與現有文獻解非常接近,相對誤差均在工程允許范圍內。從而驗證了本文方法的有效性。
2.3 彈性地基圓形加肋板的自由振動分析
2.3.1 彈性地基單肋條圓板的自由振動分析
在本算例中,一完全固支的彈性地基單肋條圓形加肋板的幾何參數為R=1.0 m,hp=0.012 m,hs=0.1 m,ts=0.01 m。板和肋條均采用相同的材料,E=206 GPa,μ=0.3,ρ=7 850 kg/m3,λ=6.0×104N/m3。圓板用169個節點離散,肋條用15個節點離散。同時,用ABAQUS軟件對圓形加肋板進行三維建模,分析其自振頻率。用S4R單元模擬圓板和肋條。將本文方法計算得到的解與ABAQUS的結果進行比較,結果如表5和圖8所示。用本文方法和ABAQUS得到的彈性地基圓形加肋板的第1階振型圖如圖9和圖10所示。
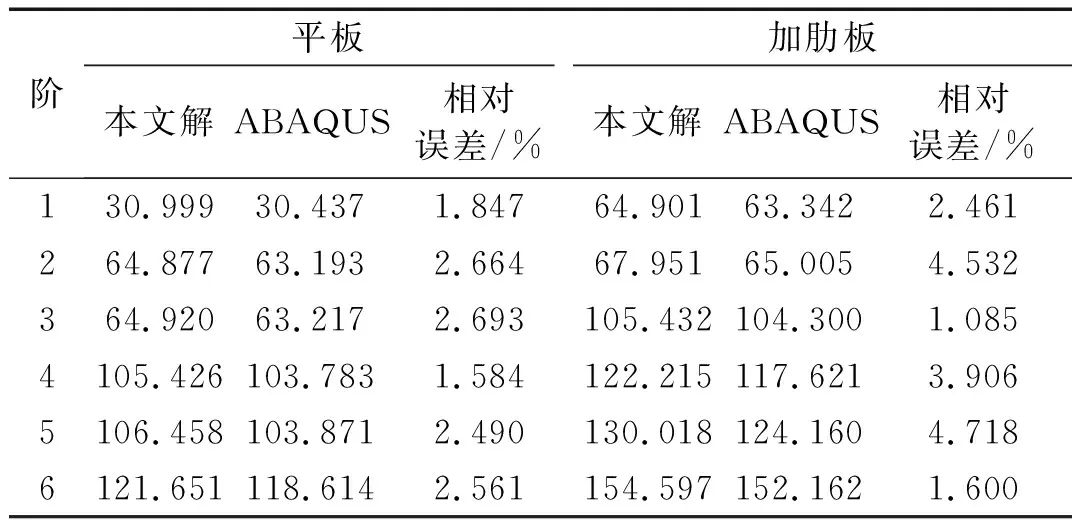
表5 彈性地基圓形平板和加肋板的頻率
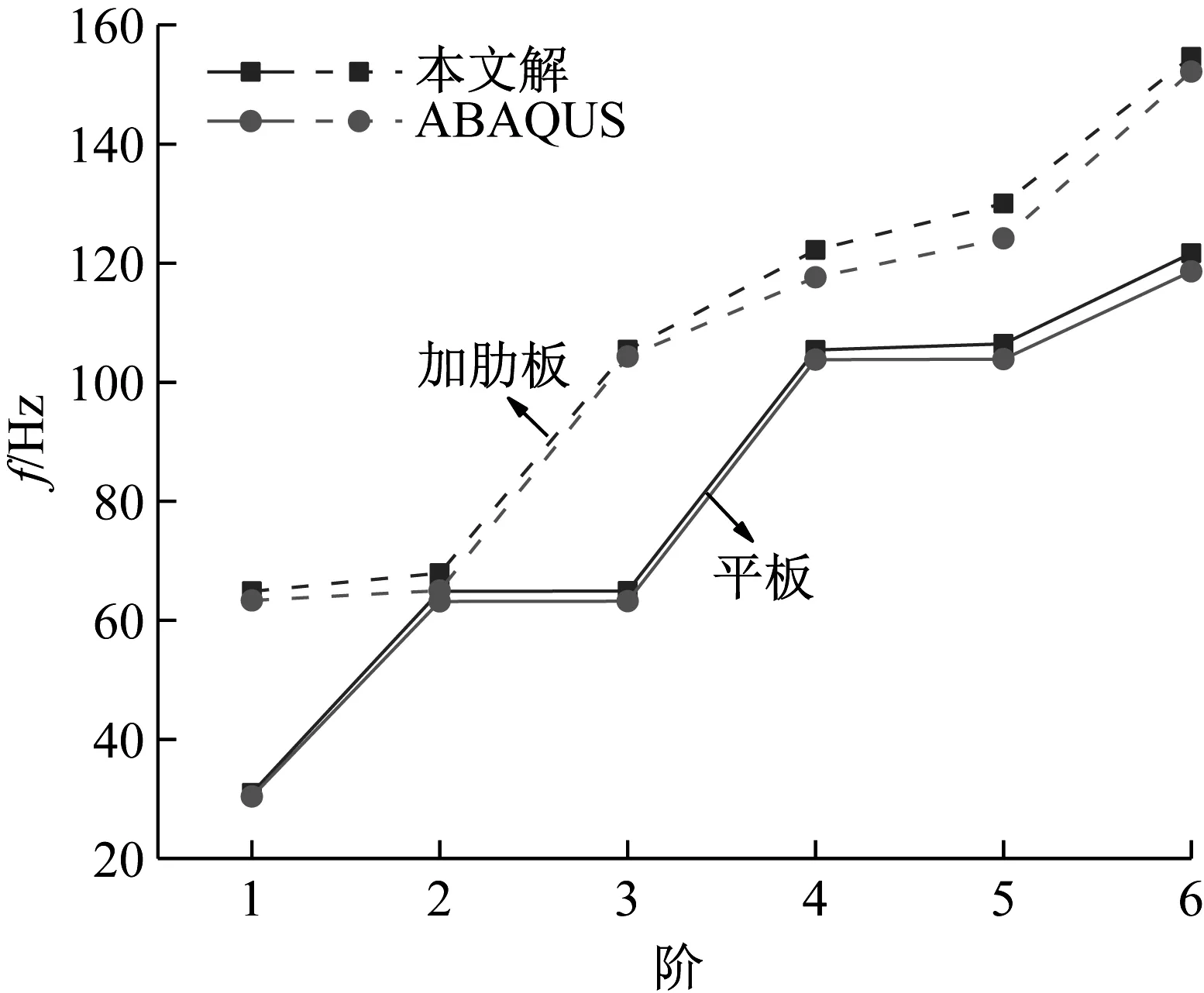
圖8 本文頻率解與ABAQUS的頻率結果對比
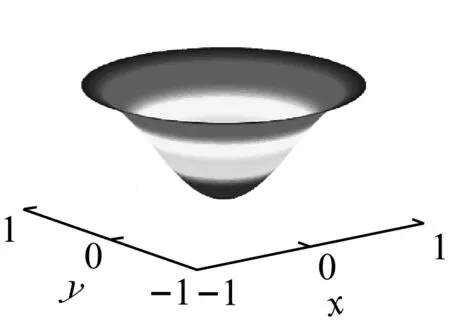
(a) 圓形平板

(a) 圓形平板
結果表明,本文解和有限元解的相對誤差都小于5%, 充分證明了本文方法的有效性和準確性。此外,從數據可以看出,加肋板的頻率明顯大于平板,這表明肋條對平板具有一定的約束作用。
2.3.2 彈性地基雙肋條圓板自由振動分析
一彈性地基上的雙肋條圓形加肋板如圖11所示,其幾何參數為R=1.5 m,hs=0.12 m,hp、ts均為0.015 m,肋條的材料和板相同,材料參數為E=29.8 GPa,μ=0.2,λ=5.0×104N/m3,ρ=2 549 kg/m3。圓板采用169個節點離散,肋條采用15個節點離散。不同邊界條件下彈性地基圓形加肋板的自振頻率如表6所示。將其與ABAQUS的結果進行了比較,相應的結果對比曲線如圖12所示。用本文方法和ABAQUS得到的彈性地基雙肋條圓形加肋板的第1階振型分別如圖13和圖14所示。
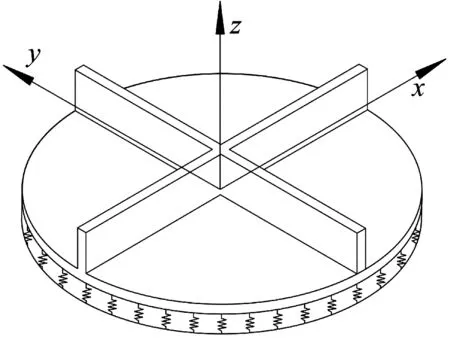
圖11 彈性地基雙肋條圓形加肋板
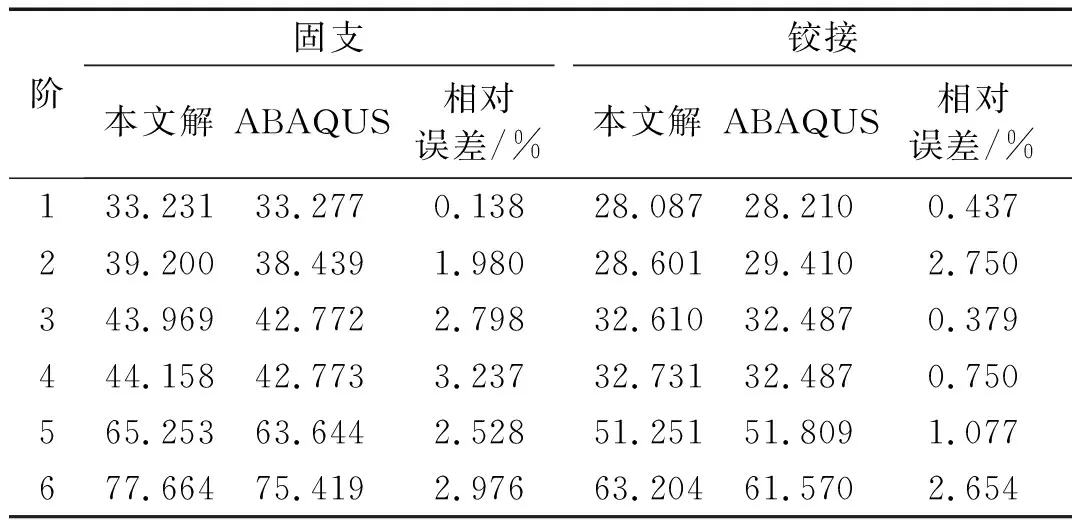
表6 不同邊界下彈性地基圓形加肋板的頻率
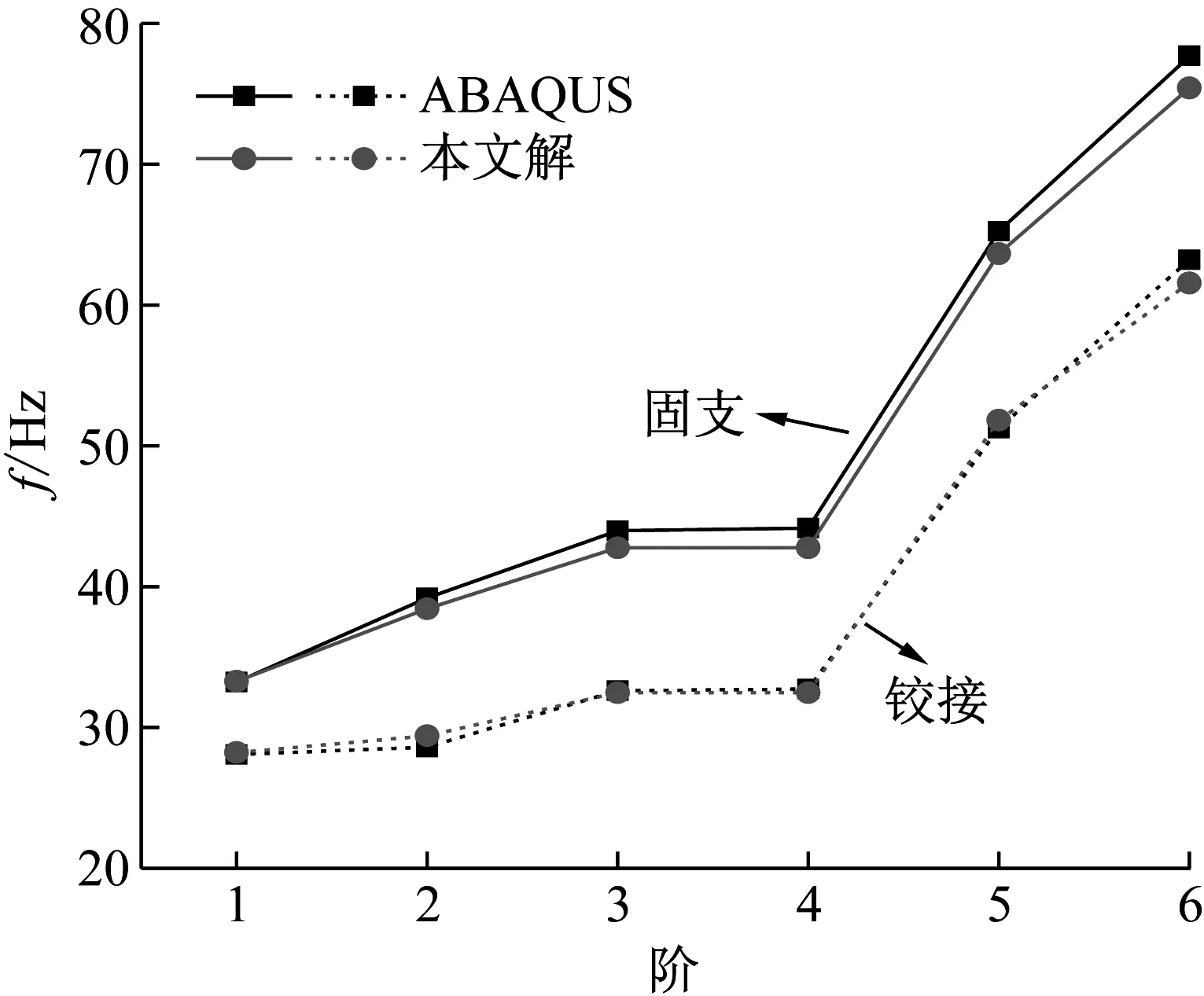
圖12 本文頻率解與ABAQUS的頻率結果對比

(a) 固支

(a) 固支
如果肋條位置發生變化(圖15),本文方法無需重新布置圓板和肋條的節點,僅需重新計算式(14)中的矩陣TP。而在ABAQUS計算中,所有的有限元網格都需要重構。兩種方法計算得到的肋條位置改變時彈性地基圓形加肋板的自振頻率如表7所示,兩種方法得到結果的一致性較好。由于本文方法在肋條位置改變后無需重新布置節點,故適用于肋條位置的優化。在肋條位置的數千次優化嘗試中,省去了繁雜的網格重置工作,從而可見該方法在肋條位置重分布的結構優化計算方面具有很大的優勢。
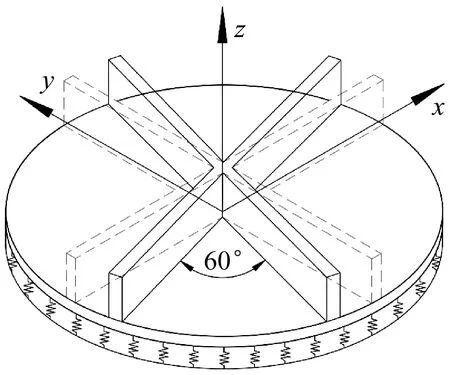
圖15 肋條位置改變的彈性地基圓形加肋板
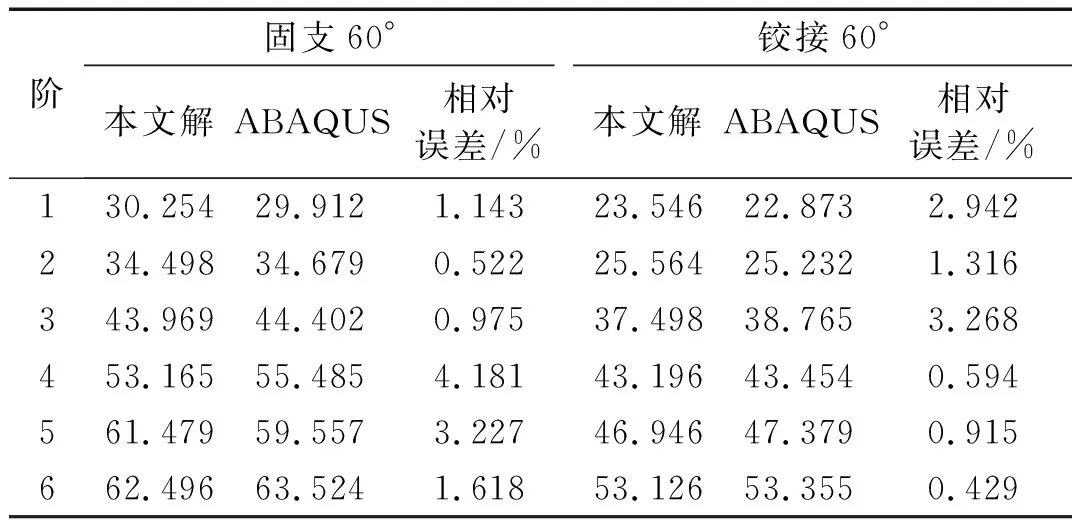
表7 肋條位置改變的彈性地基圓形加肋板頻率
2.4 圓形加肋板的靜力彎曲分析
2.4.1 鉸接單肋條圓板的靜力彎曲分析
一鉸接彈性地基單肋條圓板如圖16所示,其幾何和材料參數為R=1.4 m,hp=0.03 m,hs=0.3 m,ts=0.02 m,彈性模量E和泊松比μ分別為29.8 GPa和0.2,λ=6.0×104N/m3。結構受均布荷載集度大小為3 Pa。平面圓板采用169個節點離散,肋條采用15個節點離散。為了驗證肋條的作用,對相同尺寸的彈性地基無肋條圓板也進行了研究。板沿y=0方向的撓度計算結果如表8所示。用本文方法和ABAQUS得到的位移云圖分別如圖17和圖18所示,相應的結果對比如圖19所示。結果表明,本文解與有限元解非常接近。此外,加肋板的撓度明顯小于無加肋平板,這意味著肋條起到了一定的約束作用。
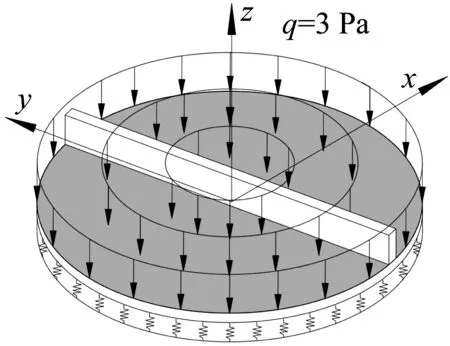
圖16 受均布荷載作用下的彈性地基圓形加肋板
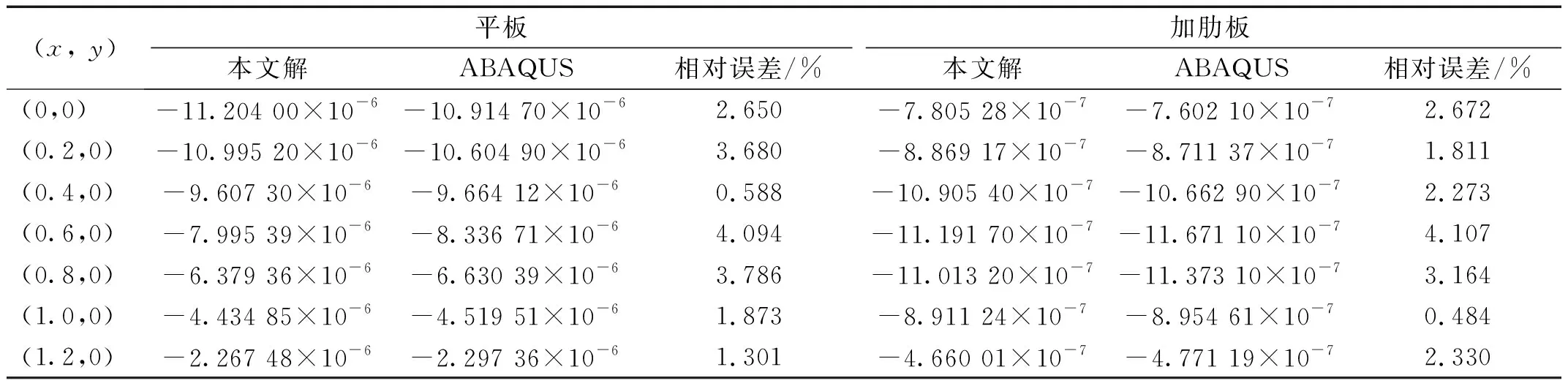
表8 彈性地基加肋板沿y=0方向的撓度

(a) 圓形平板
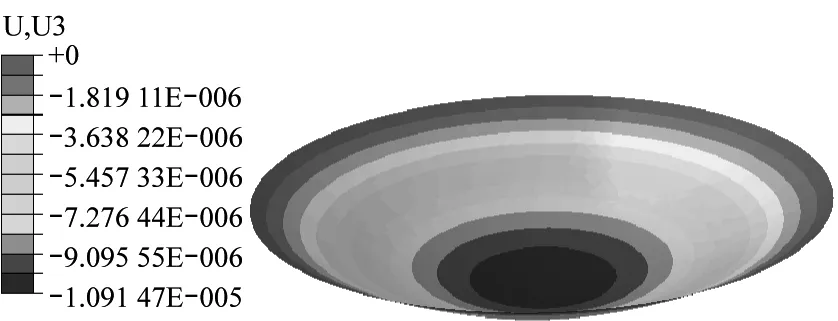
(a) 圓形平板
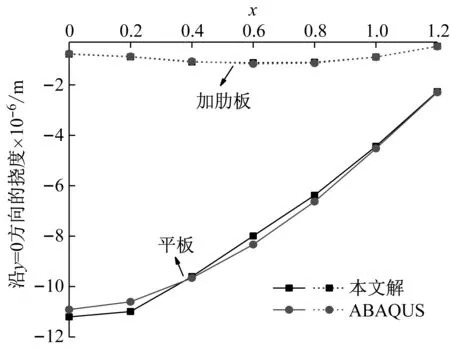
圖19 本文撓度解與ABAQUS的結果對比
2.4.2 彈性地基雙肋條圓形加肋板的靜力彎曲分析
為了進一步驗證本文方法在彈性地基圓形加肋板靜力分析中的有效性,將兩個雙肋條圓板分別固支與鉸接,如圖20所示。它們的幾何參數為R=0.7 m,hs=0.15 m,hp、ts均為0.02 m。材料參數為:楊氏模量E和泊松比μ分別為17 MPa和0.3,λ=4.0×104N/m3。彈性地基加肋板受局部均布荷載q=2 Pa。將169個節點用于離散平板,15個節點用于離散每一根肋條。板沿y=0方向的撓度計算結果如表9所示。用本文方法和ABAQUS得到的位移云圖分別如圖21及圖22所示,相應的結果對比如圖23所示。
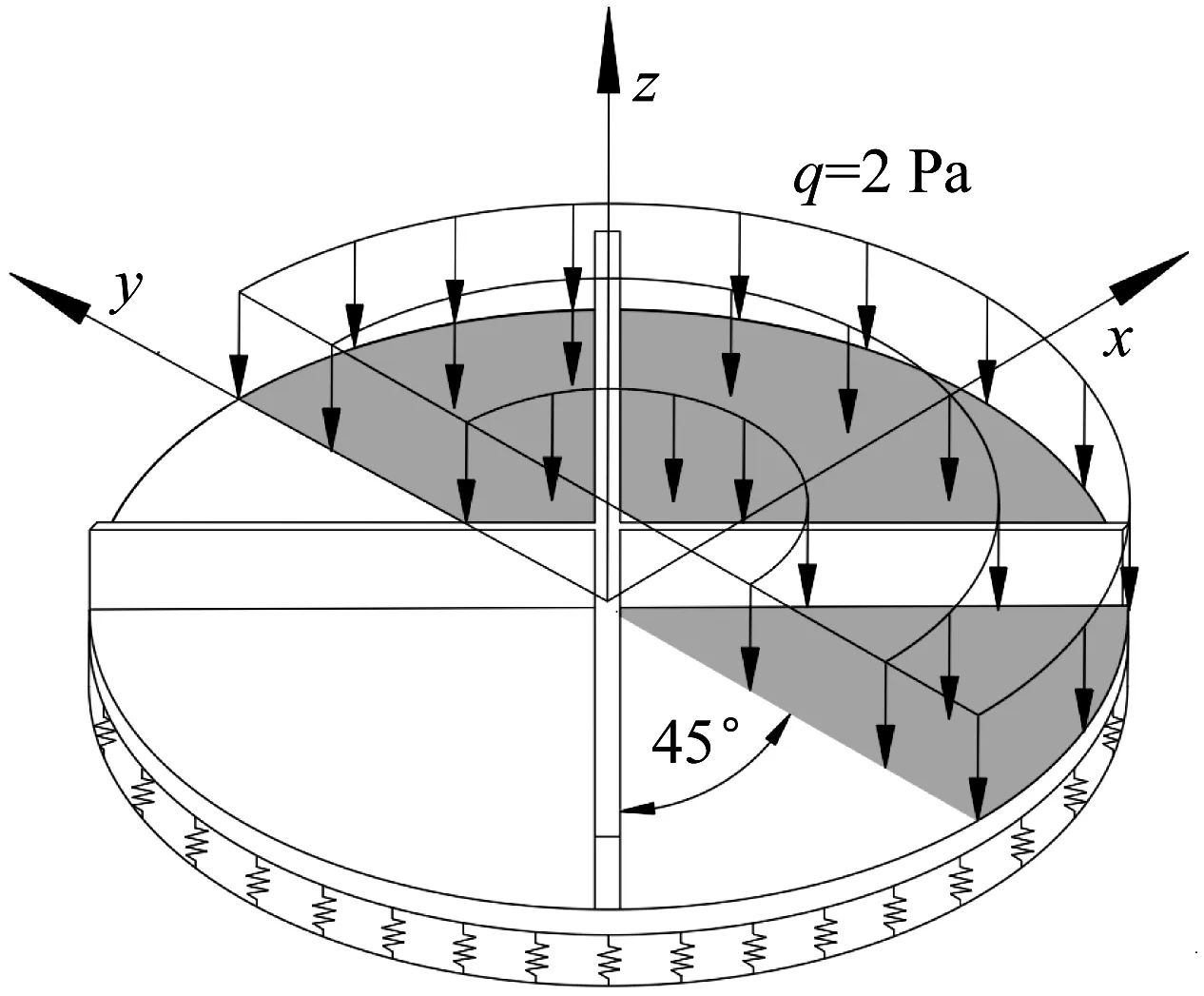
圖20 彈性地基雙肋條圓板受局部均勻荷載
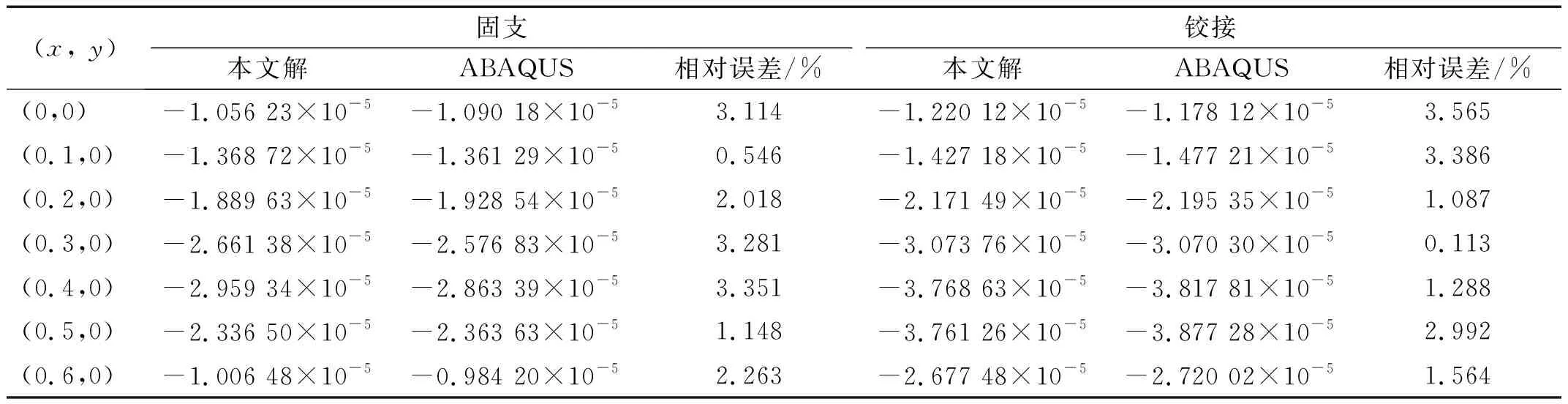
表9 彈性地基加肋板沿y=0方向的撓度
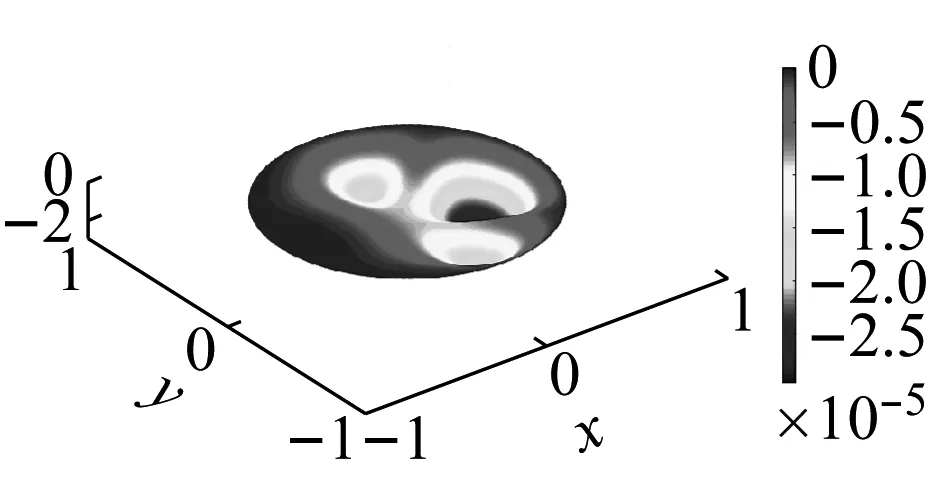
(a) 固支
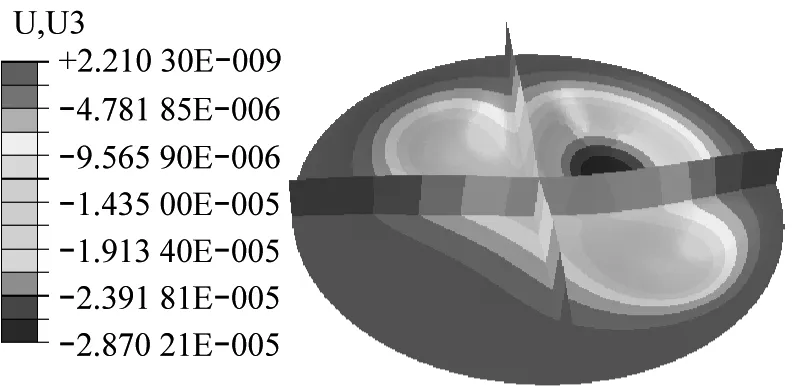
(a) 固支
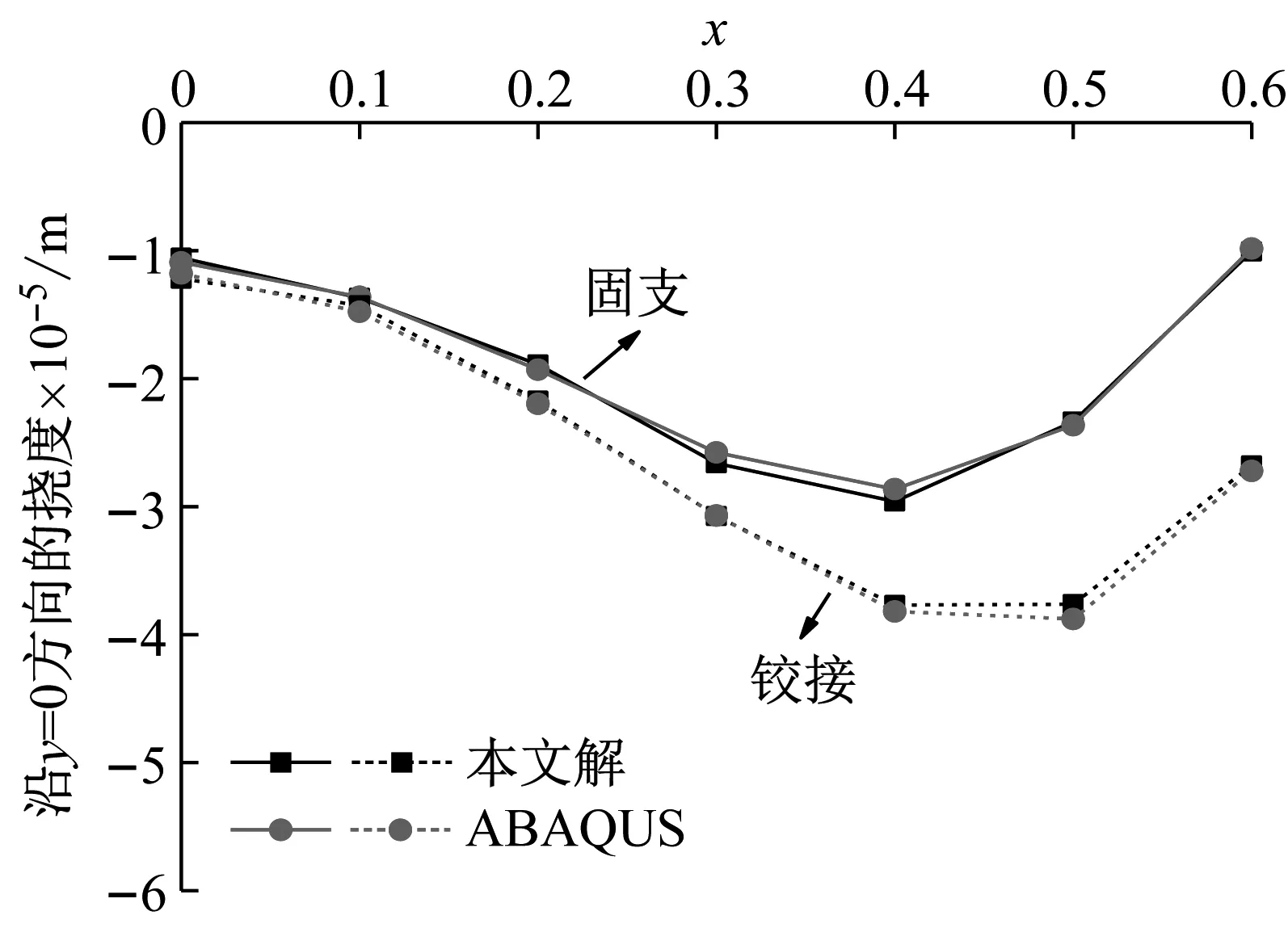
圖23 本文解與ABAQUS的撓度對比
結果表明,本文解與有限元解非常接近。另外,從計算結果也可以看出,完全固支的加肋板撓度明顯小于鉸接加肋板的撓度,這表明了不同邊界條件具有不同的約束作用。
如果肋條位置發生變化(圖24),本文方法無需重新布置板和肋條的節點,只需重新計算式(14)中的矩陣TP即可重新計算板的撓度(表10)。而在有限元法中,所有網格都需要重新劃分。該算例表明,本文方法可用于局部均布荷載作用下的肋條位置優化。
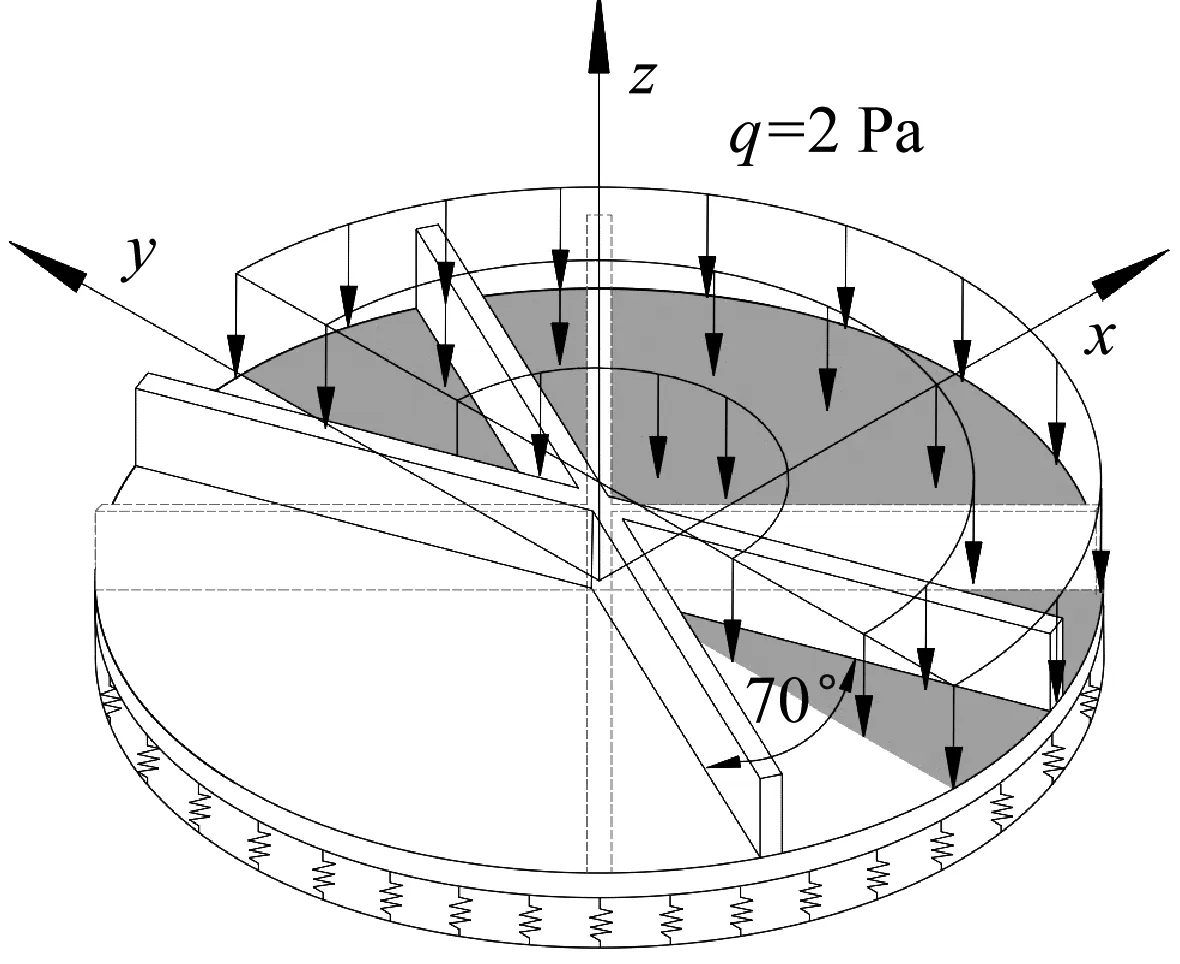
圖24 肋條位置改變的彈性地基圓形加肋板
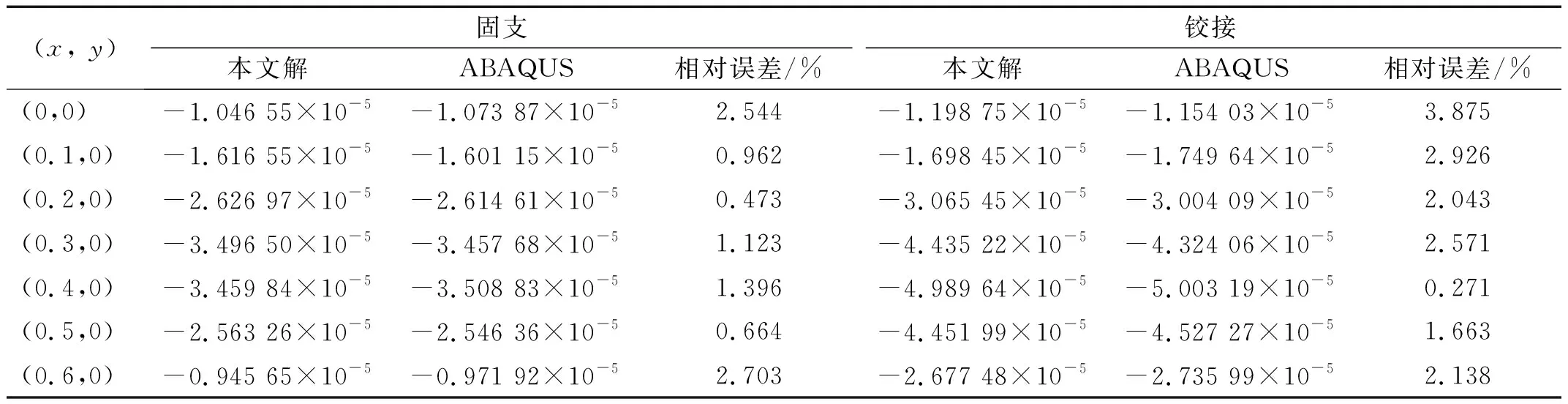
表10 肋條位置改變的彈性地基圓形加肋板的撓度
3 結 論
基于一階剪切理論和移動最小二乘法,提出分析彈性地基上圓形加肋板彎曲的靜力及自由振動問題的無網格法。文中以不同基床系數、邊界條件、肋條布置形式的加肋板為例,將本文結果與有限元、文獻結果對比,得出了以下結論:
(1) 本文方法收斂速度快,計算穩定性好。對于直徑是0.5 m的彈性地基加肋板,在節點數達到169個時,結果收斂;影響域因子dmax大于3.0時,結果趨于穩定。
(2) 本文解與有限元、文獻解吻合好,相對誤差在工程允許范圍內。在不同的基床系數、荷載、邊界及肋條布置方式下,本文方法可有效分析彈性地基上圓形加肋板線性彎曲的靜力和自由振動問題。
(3) 基于加肋板與肋條的離散點,通過兩者在接觸位置的位移協調建立了參數轉換方程,點與點之間沒有任何單元連接,當肋條位置改變時,肋條與板各自的離散點不會發生改變。因此,本文方法可以實現肋條在圓板上任意布置,而不需要網格重置,只需重新計算轉換矩陣,非常適用于肋條優化工作的研究。

