基于阻抗和功率守恒法的地鐵車輛段上蓋建筑車致振動預(yù)測模型研究
陶子渝, 汪益敏, 鄒 超
(1.華南理工大學(xué) 土木與交通學(xué)院,廣州 510641; 2.廣東工業(yè)大學(xué) 土木與交通工程學(xué)院,廣州 510006)
隨著我國城市化的發(fā)展和城鎮(zhèn)人口的快速增長,地鐵車輛段上蓋物業(yè)開發(fā)能高效利用城市土地資源,實現(xiàn)“一地兩用”,從經(jīng)濟(jì)上反哺城市地鐵系統(tǒng)運(yùn)營,已成為我國地鐵車輛段建設(shè)趨勢。
帶上蓋建筑地鐵車輛段需要建設(shè)鋼筋混凝土框架大平臺結(jié)構(gòu)(圖1),首層平臺覆蓋整個地鐵車輛段,通常用作汽車停車場,該平臺既能起到保護(hù)地鐵車輛段正常運(yùn)營,不受上部活動作業(yè)干擾,又能使得地鐵車輛在蓋下運(yùn)行,減輕了自然環(huán)境影響。在首層平臺之上再施工上蓋建筑可與地鐵車輛段的運(yùn)營平行作業(yè),互不干擾,最終形成立體開發(fā)模式。但研究表明,列車運(yùn)行引起的結(jié)構(gòu)振動和噪聲制約著地鐵車輛段上蓋物業(yè)開發(fā)[1-5],地鐵車輛段環(huán)境振動與噪聲問題成為近年來的研究熱點。
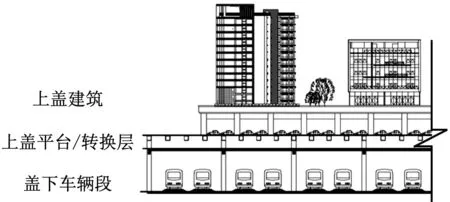
圖1 帶上蓋建筑地鐵車輛段示意圖
現(xiàn)場測試結(jié)果表明[6-8],地鐵車輛段試車線和咽喉區(qū)的列車運(yùn)行對上蓋建筑振動影響最大。試車線運(yùn)行車速較高,一般在20~80 km/h,通常采用了高等級減振措施,如橡膠墊、梯形軌枕等。對于咽喉區(qū),盡管列車以10~20 km/h的速度低速通過,但由于咽喉區(qū)存在大量道岔、接頭、小半徑曲線軌道,且平臺結(jié)構(gòu)柱與軌道之間距離較短(圖1),列車行經(jīng)該區(qū)域時仍將引起上蓋建筑較大的振動響應(yīng)。
研究地鐵車輛段上蓋結(jié)構(gòu)振動預(yù)測模型有利于指導(dǎo)設(shè)計經(jīng)濟(jì)合理的減隔振措施,保證上蓋建筑物室內(nèi)振動與噪聲達(dá)到宜居標(biāo)準(zhǔn)。經(jīng)驗公式是常見的預(yù)測模型之一,美國聯(lián)邦交通管理局對交通運(yùn)輸產(chǎn)生的噪聲與振動評價指南[9]中采用了經(jīng)驗?zāi)P皖A(yù)測列車運(yùn)行引起的振動響應(yīng),雖然該模型方法簡單易行,但預(yù)測精度不高,且模型物理意義不明確。
數(shù)值模型也被應(yīng)用于預(yù)測列車運(yùn)行引起的結(jié)構(gòu)振動,Guo等[10]采用有限元模型分別對停車列檢庫上蓋框架結(jié)構(gòu)和高架模式地鐵車輛段的振動響應(yīng)進(jìn)行了分析,研究均表明車輛段車致結(jié)構(gòu)振動存在超標(biāo)現(xiàn)象。數(shù)值模型能模擬工程復(fù)雜的幾何形狀和邊界條件,但計算耗時長,成本高,處理大型結(jié)構(gòu)或高頻振動問題時,面對巨大的自由度和單元數(shù)目,甚至無法求解。
Sanayei等[11-12]研究列車運(yùn)行引起的結(jié)構(gòu)振動時,基于結(jié)構(gòu)柱軸向波傳播提出了阻抗模型,該模型計算效率高且簡單易行,可有效預(yù)測上蓋建筑柱腳附近的振動響應(yīng),但是對上蓋建筑樓板中心的振動響應(yīng)還無法通過模型計算得出。實測表明,樓板中心的豎向振動可比柱腳附近高出10 dB以上,對居民工作與生活的影響更大。
本文以深圳地鐵某車輛段上蓋4層鋼框架結(jié)構(gòu)為依托,基于波動理論,考慮了軸向波在結(jié)構(gòu)柱和彎曲波在結(jié)構(gòu)梁中的傳播,推導(dǎo)了梁板組合效應(yīng)下梁端驅(qū)動點阻抗;基于阻抗和功率守恒法建立車輛段地鐵運(yùn)行引起的上蓋框架結(jié)構(gòu)柱腳及樓板的振動響應(yīng)預(yù)測模型,并根據(jù)現(xiàn)場實測數(shù)據(jù)對模型進(jìn)行了驗證,研究成果可為地鐵車輛段上蓋建筑車致振動控制設(shè)計提供科學(xué)方法和依據(jù)。
1 工程概況
研究對象為深圳地鐵某車輛段咽喉區(qū)上蓋一座4層鋼框架結(jié)構(gòu),如圖2所示。樓板為壓型鋼板組合板,建筑材料采用的鋼號和混凝土標(biāo)號分別為Q345B和C30。該車輛段運(yùn)營6節(jié)編組的空載A型列車,咽喉區(qū)軌道位于此上蓋建筑正下方,采用有砟道床(圖3)。
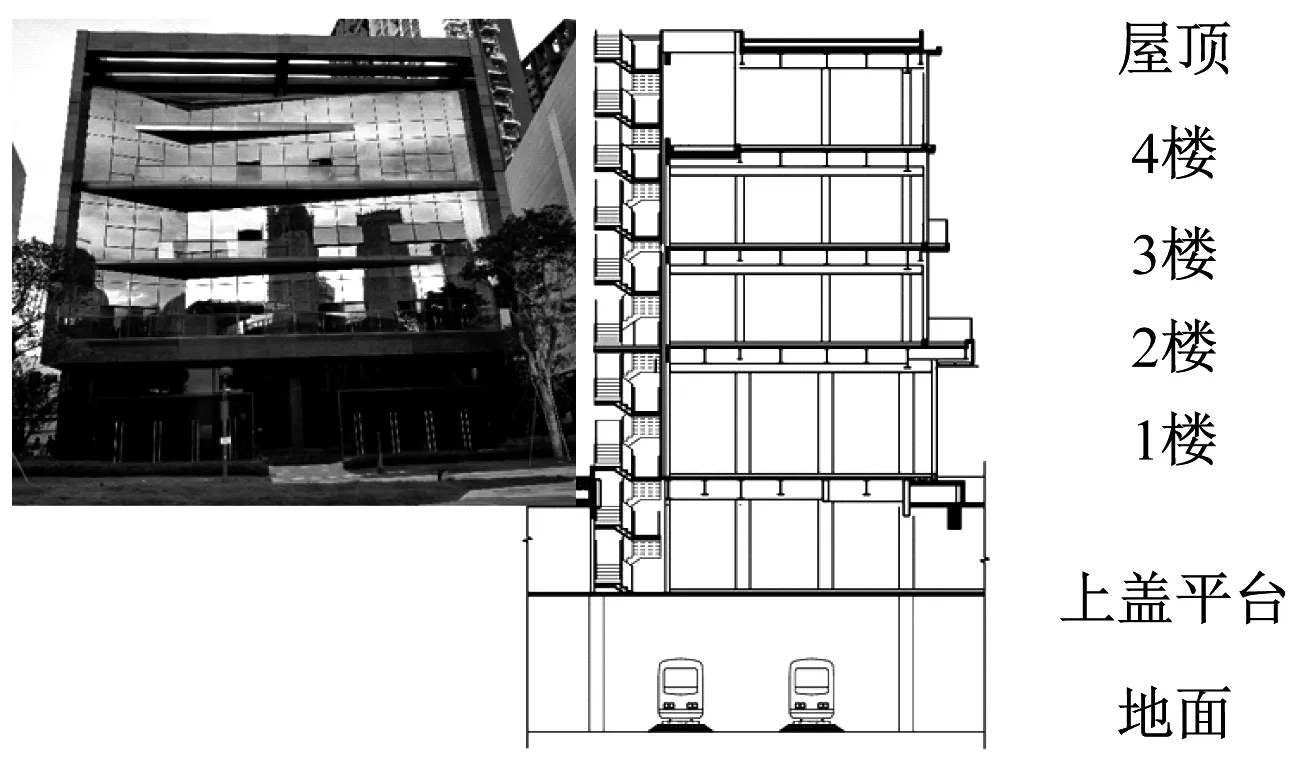
圖2 咽喉區(qū)上蓋4層鋼框架結(jié)構(gòu)

圖3 咽喉區(qū)軌道
4樓平面圖及測試點位,如圖4所示。該樓層布設(shè)了1個柱腳測點(GZ3)和一個樓板測點(測點A),其他樓層(1~3樓)測點布設(shè)位置相同。試驗共采集了18組咽喉區(qū)有效車次通過時的樓板振動加速度,采樣頻率512 Hz,詳細(xì)現(xiàn)場試驗分析可參見Tao等的數(shù)據(jù)。
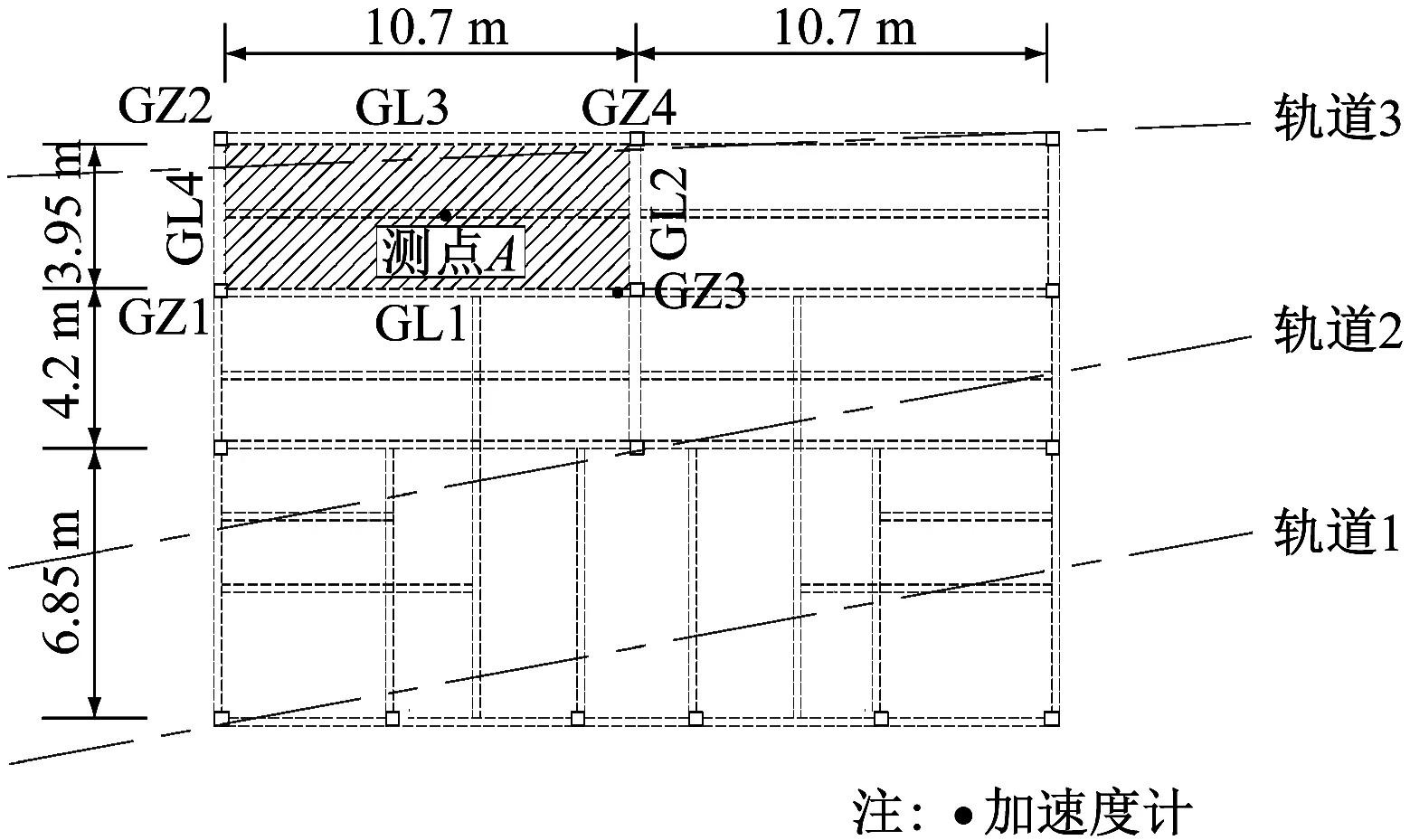
圖4 4樓平面圖及測點布設(shè)
表1列舉了空心鋼管柱GZ1~GZ4沿各樓層的尺寸特性。圖4中陰影范圍表示第二個子模型中樓板時空平均振動的預(yù)測區(qū)域,該區(qū)域的4根主梁截面尺寸詳見表2。鋼和混凝土的材料設(shè)計參數(shù)見表3。
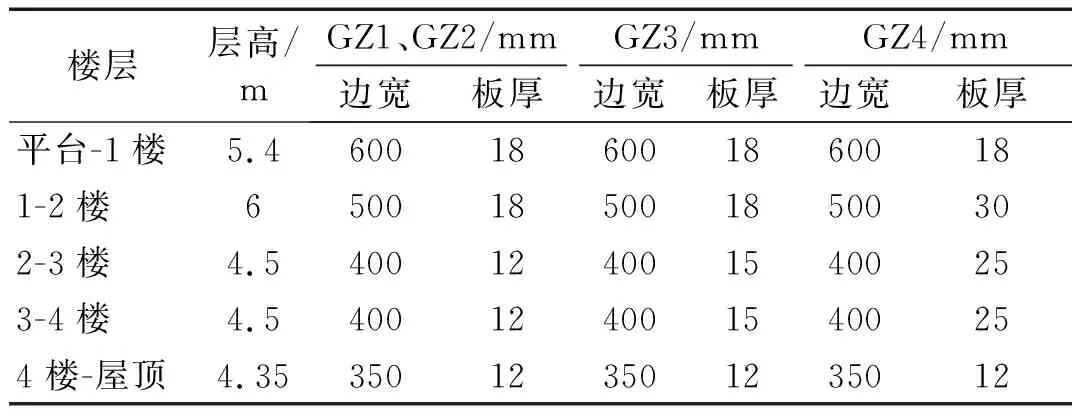
表1 鋼柱截面尺寸表

表3 材料設(shè)計參數(shù)表
2 預(yù)測模型建立
為預(yù)測上蓋建筑樓板車致振動響應(yīng),所提出的振動預(yù)測模型(圖5)根據(jù)波傳播路徑包含兩個級聯(lián)子模型,第一個子模型基于阻抗法以平臺柱腳實測速度作為輸入預(yù)測了上蓋建筑各樓層柱腳振動響應(yīng),第二個子模型以第一個子模型柱腳振動響應(yīng)預(yù)測作為輸入,考慮梁板組合效應(yīng),基于功率守恒原理預(yù)測樓板時空平均振動響應(yīng)。
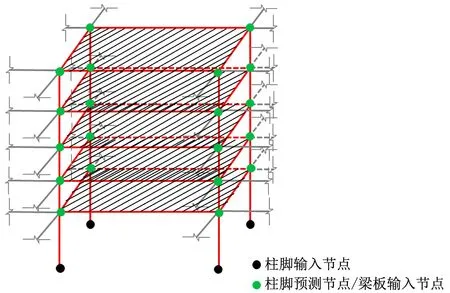
圖5 預(yù)測模型示意圖
2.1 阻抗模型
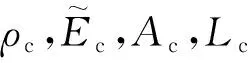
(1)
圖6為該上蓋4層建筑的阻抗模型組裝示意圖,各層樓板用無限薄板的點阻抗(式(2))表征,通過各樓層節(jié)點受力平衡可得出系統(tǒng)方程(3)。若已知柱腳速度輸入vinput,則樓上各層柱腳速度響應(yīng)預(yù)測vi可通過求解系統(tǒng)方程(3)得出。
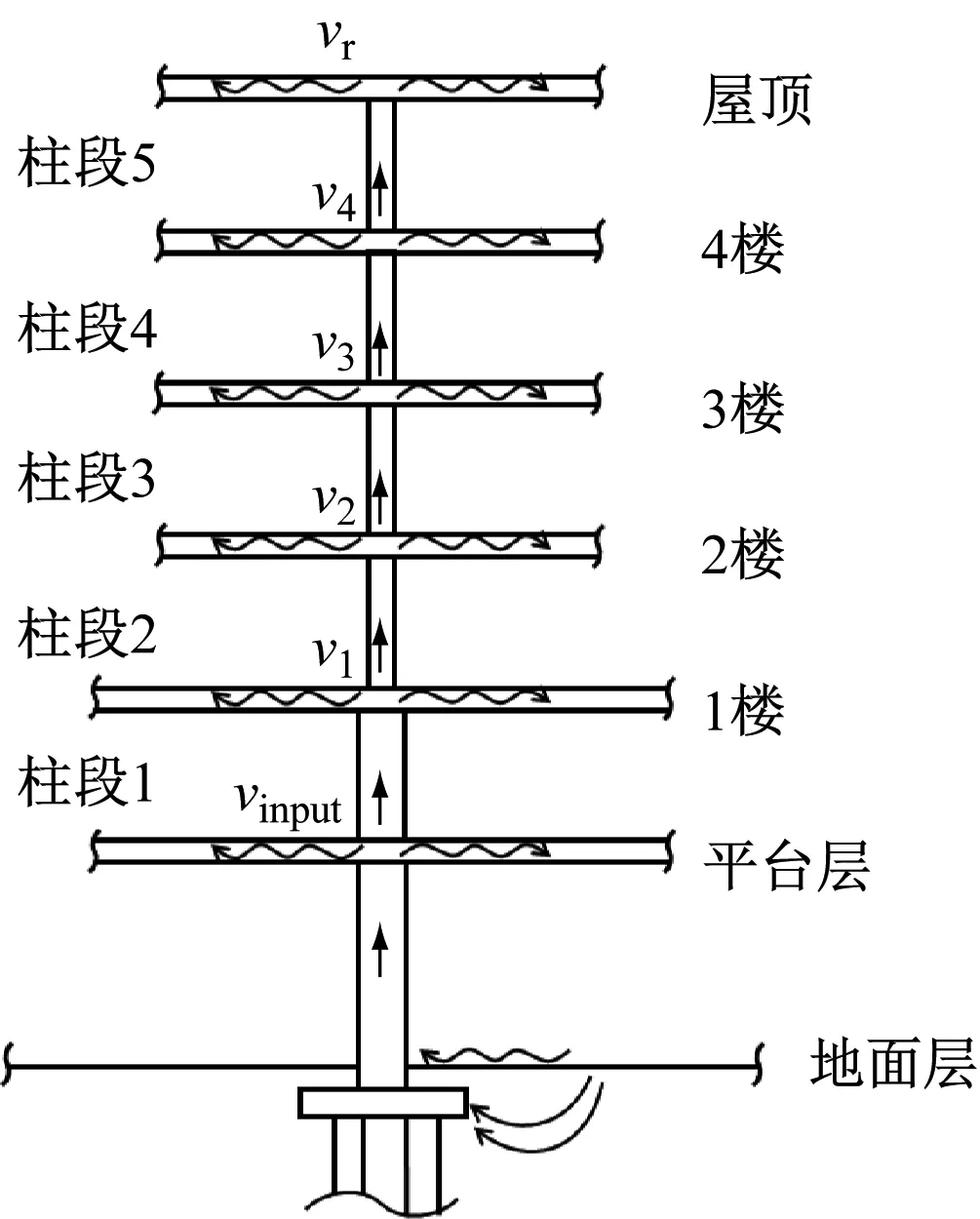
圖6 阻抗模型
(2)
[Z]{V}={F}
(3)
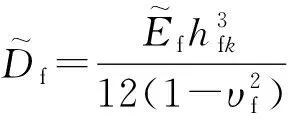
系統(tǒng)方程(3)中,[Z]為系統(tǒng)阻抗矩陣,基于柱段連接方式,其通常為窄帶寬對稱陣,對于本研究中的4層結(jié)構(gòu)其具體展開為
2.2 梁板組合效應(yīng)
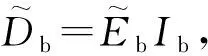
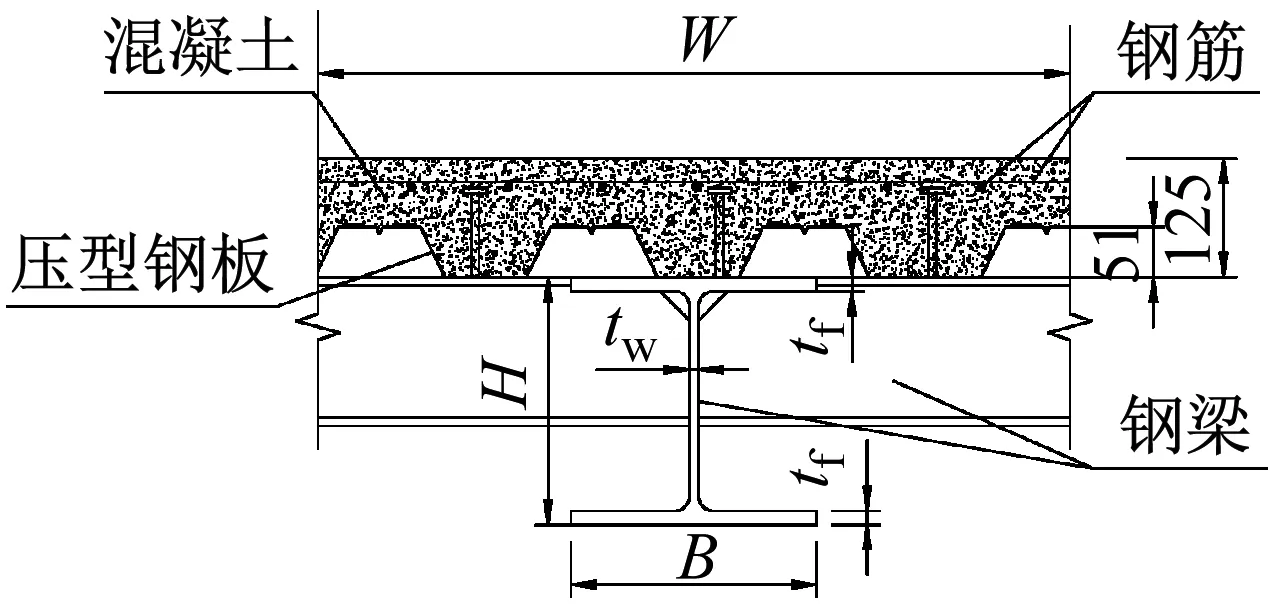
圖7 壓型鋼板組合板(mm)

表4 鋼梁抗彎剛度
2.3 梁的驅(qū)動點阻抗
在考慮梁板組合效應(yīng)下,基于機(jī)械波理論,本節(jié)推導(dǎo)了有限長梁的驅(qū)動點阻抗[13]。圖8為單跨梁端點簡諧激勵下梁內(nèi)彎曲波示意圖,圖中沿x軸正向傳播彎曲波由簡諧激勵產(chǎn)生,負(fù)向傳播波為反射波,其與x=Lb端點處的具體邊界條件有關(guān)。

圖8 單跨梁端點激勵下梁內(nèi)彎曲波示意圖
根據(jù)圖8,梁的豎向位移可以表示為
(4)
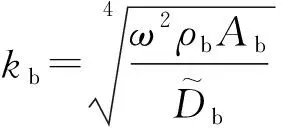
代入x=0處邊界條件,便可求得梁的驅(qū)動點阻抗。由圖4可見,預(yù)測區(qū)域內(nèi),激勵梁端存在兩種邊界條件,例如,GL1在GZ1處受豎向激勵時,該端點可存在轉(zhuǎn)角,而GL1在GZ3處受豎向激勵時,由于對稱結(jié)構(gòu),該端點不可以轉(zhuǎn)動,僅存在豎向位移。表5給出了兩種不同激勵點邊界條件下,梁的驅(qū)動點阻抗表達(dá)式。
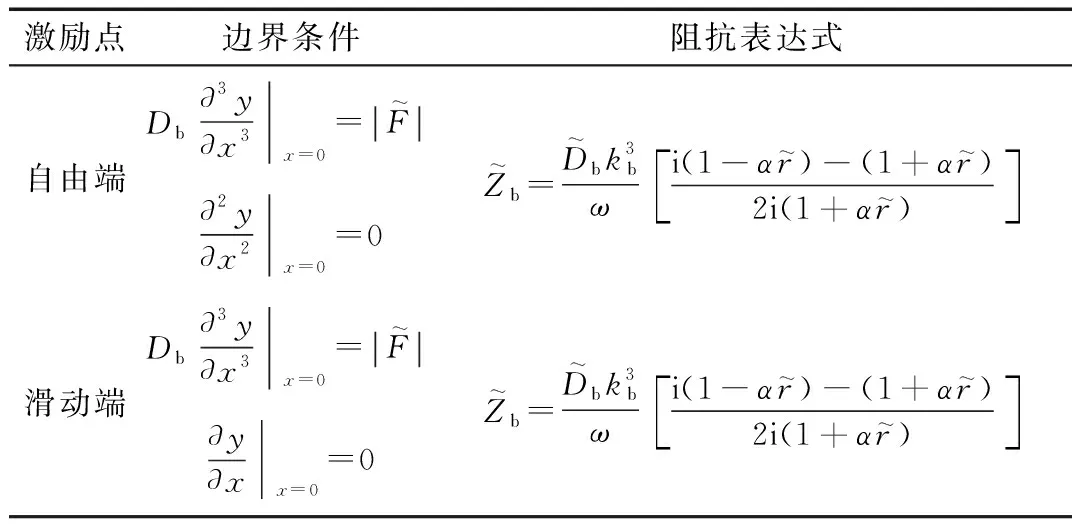
表5 梁的驅(qū)動點阻抗
2.4 功率守恒模型
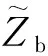
(5)
由功率守恒
(6)
式中:f為由預(yù)測樓板消耗的機(jī)械功率;ρf,Sf,ηf分別為樓板密度,面積及阻尼損耗因子;vf為預(yù)測樓板范圍內(nèi)時空平均速度;∑b,i為預(yù)測樓板范圍內(nèi)來自各梁的功率輸入和。通過聯(lián)立式(5)和(6),即可獲得樓板時空平均速度預(yù)測值。
3 計算結(jié)果分析及模型驗證
3.1 梁端點阻抗比較
以鋼梁GL1為例,圖9比較了不同工況下其激勵端點阻抗。由圖可見,梁板組合效應(yīng)顯著增加了梁端點阻抗。在有限長梁模型中由于彎曲波的反射會引起明顯的共振現(xiàn)象,相比之下,半無限長梁模型則起到了頻率平均作用。滑動端激勵工況下,其梁端點阻抗的共振頻率比自由端激勵時大,這是因為滑動端較自由端限制了轉(zhuǎn)動自由度,導(dǎo)致梁的整體剛度增加,從而自振頻率向高頻移動。
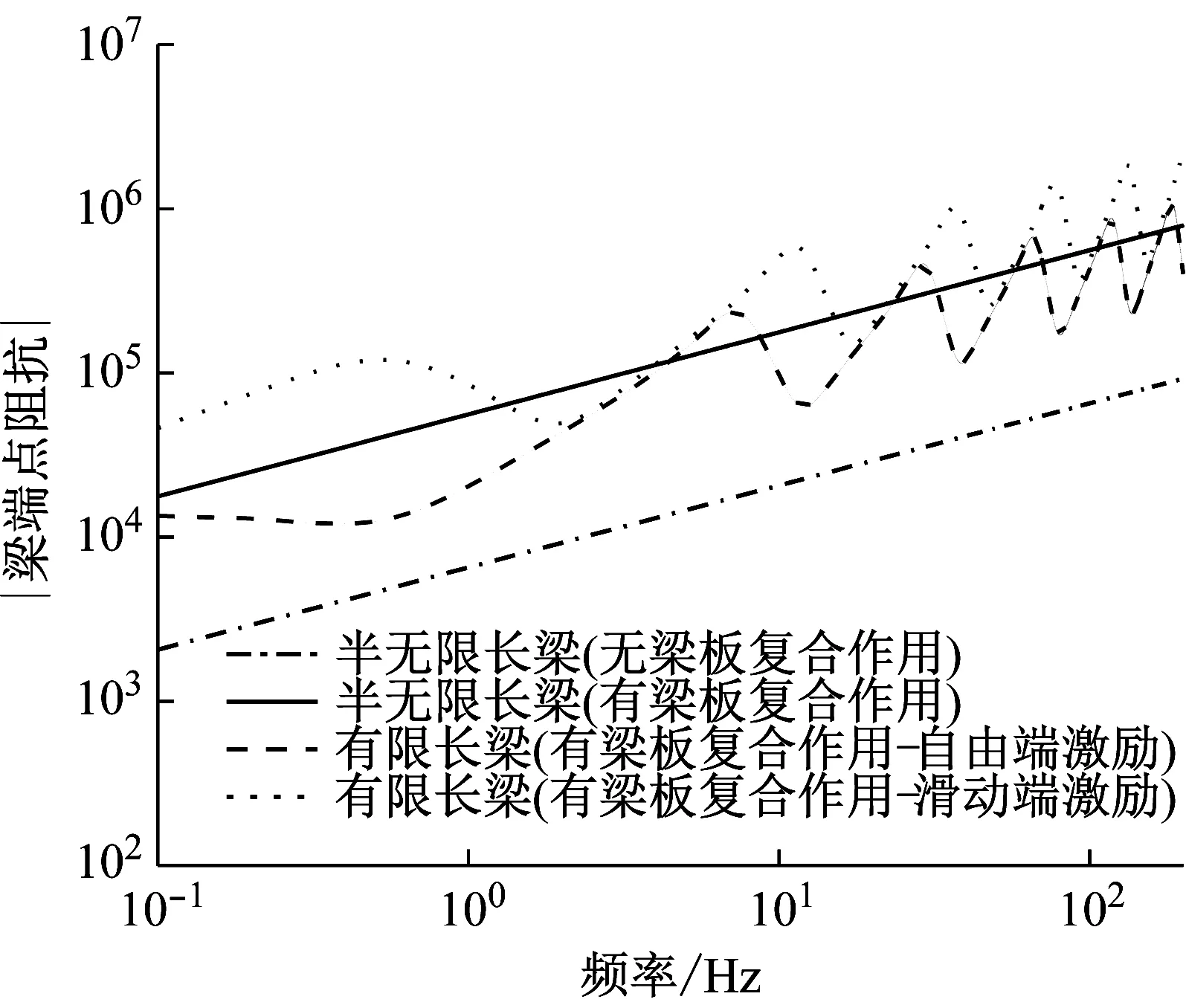
圖9 不同工況下梁端點阻抗比較
3.2 模型驗證
為了驗證預(yù)測模型可靠性,首先將子模型一計算的GZ3各層柱腳振動預(yù)測值與實測值進(jìn)行了對比。圖10為GZ3平臺柱腳實測速度的三分之一倍頻程譜,作為整個預(yù)測模型的最底層輸入。圖11比較了各樓層柱腳實測值及預(yù)測值。從圖中可以看出,該車輛段上蓋建筑車致振動存在10 Hz和31.5 Hz兩個頻率峰值,這與結(jié)構(gòu)自振頻率和列車荷載激振頻率有關(guān)。車致振動向上傳播過程中,高頻分量衰減較低頻快,因此隨著樓層的增加,振動低頻分量的比重也在增加。子模型一能成功預(yù)測上蓋建筑各層柱腳的振動主頻,峰值頻率處振動預(yù)測值與實測值之間差異在5 dB以內(nèi)。
子模型一預(yù)測精度隨著樓層的增加有所降低,這與模型簡化有關(guān),因為實際建筑在屋面層做了屋頂花園,屋頂覆土和植被對較高樓層車致振動響應(yīng)影響較大。
子模型二利用功率守恒預(yù)測樓板區(qū)域時空平均振動響應(yīng)需要知道GZ1~GZ4的柱腳振動速度,以4樓GZ1~GZ4為例,圖12為利用阻抗子模型一預(yù)測的柱腳振動速度,4根柱腳的平臺輸入都使用了如圖10所示實測值,由于該區(qū)域最大跨度為10.7 m,可以認(rèn)為一致輸入是合理的。由圖12可見,4根柱腳之間的振動差別不大,這與Tao等的實測結(jié)果具有一致性。
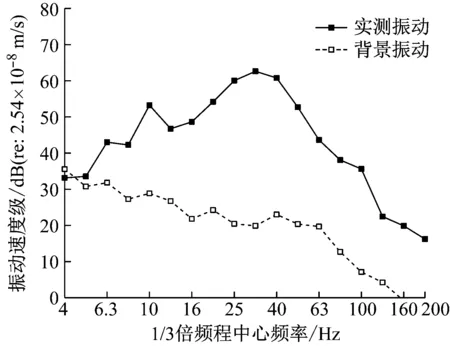
圖10 平臺柱腳實測輸入
(a) 1樓
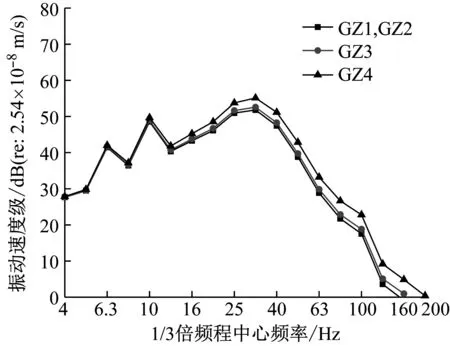
圖12 4樓GZ1-GZ4柱腳振動預(yù)測
以阻抗子模型一的計算柱腳速度作為輸入,功率子模型二可以預(yù)測各層樓板區(qū)域時空平均振動響應(yīng)。圖13將4樓預(yù)測值與測點A位置實測值進(jìn)行了比較,其他樓層預(yù)測與實測的對比結(jié)果類似,限于篇幅,故不一一示出。
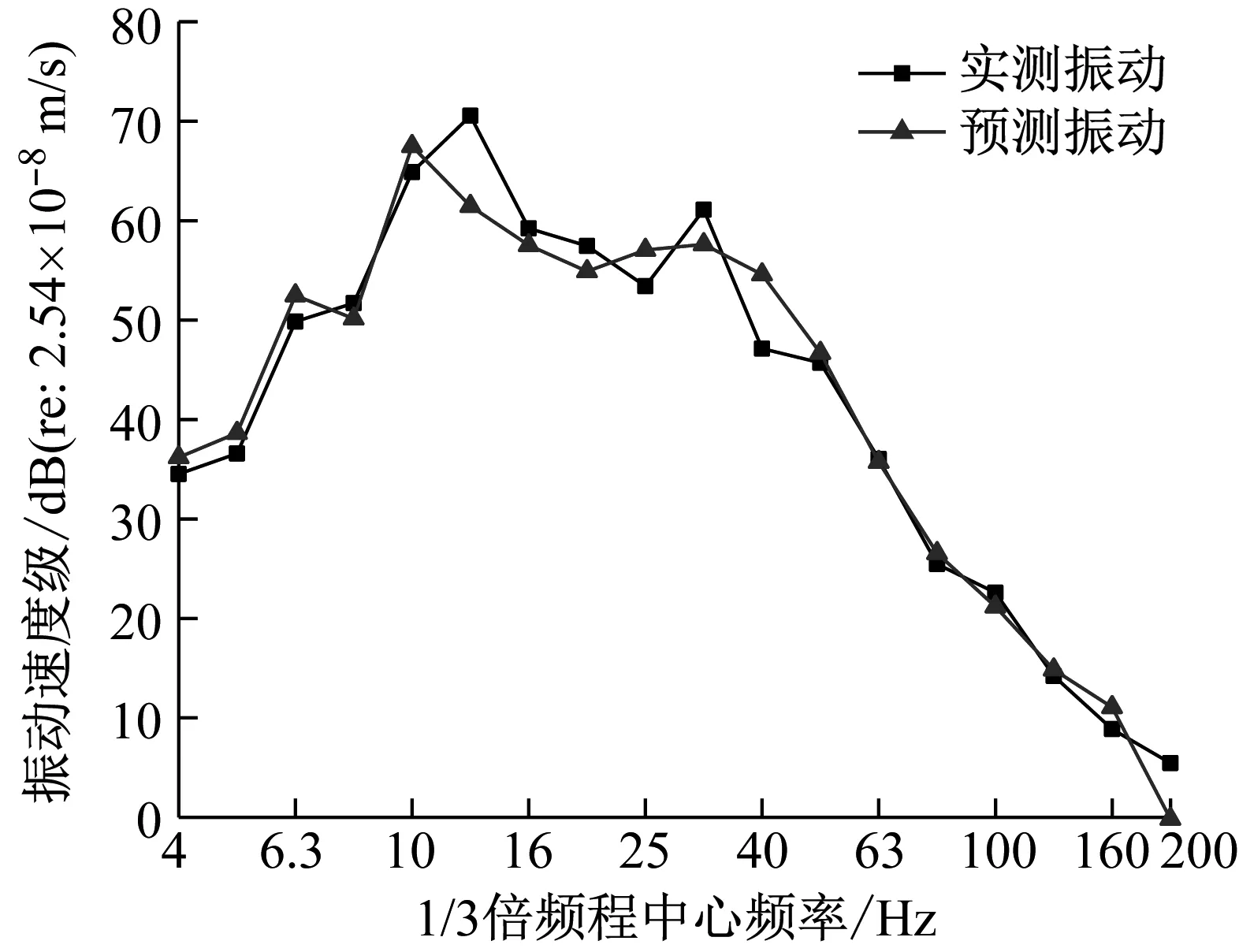
圖13 4樓樓板時空平均振動預(yù)測驗證
由圖13可見,用阻抗子模型一的柱腳預(yù)測值作為輸入,功率子模型二預(yù)測值與實測值分頻差異在7 dB以內(nèi),但是總體振動水平差異在3 dB以內(nèi)。這是因為子模型二利用功率守恒預(yù)測的樓板區(qū)域時空平均振動水平不能表征樓板復(fù)雜的振動模態(tài)振型,但是卻能從成功從能量的角度預(yù)測樓板總體振動水平。
3.3 模型精度及適用性分析
本文提出的車輛段上蓋結(jié)構(gòu)振動預(yù)測模型以波傳導(dǎo)理論為基礎(chǔ),包含級聯(lián)使用的阻抗子模型一和功率子模型二,從圖11和圖13的柱腳和樓板振動預(yù)測值和實測數(shù)據(jù)的對比可以看出,該模型預(yù)測精度良好。另外,該模型計算效率高,建模工作量小,因此適用于實際工程應(yīng)用。值得指出的是,該模型采用點阻抗的研究方法,因此只適用于框架結(jié)構(gòu)的振動響應(yīng)預(yù)測,對于高層剪力墻結(jié)構(gòu),該模型需要進(jìn)一步改進(jìn)和發(fā)展。
4 結(jié) 論
本研究以深圳地鐵某車輛段上蓋4層鋼框架結(jié)構(gòu)為依托,根據(jù)波動理論推導(dǎo)了考慮梁板組合效應(yīng)的梁端驅(qū)動點阻抗,基于阻抗和功率守恒提出了車輛段地鐵運(yùn)行引起的上蓋框架結(jié)構(gòu)柱腳及樓板時空平均振動響應(yīng)預(yù)測模型,并根據(jù)現(xiàn)場實測數(shù)據(jù)對模型進(jìn)行了驗證。該模型包含級聯(lián)使用的阻抗子模型和功率子模型,以平臺柱腳實測速度為輸入,計算時間短,預(yù)測精度較高,建模工作量小,適用于實際工程使用,可以為帶上蓋物業(yè)地鐵車輛段減隔振措施的設(shè)計提供科學(xué)方法和依據(jù)。

