面向薄壁零件的黏滯阻尼器設計及試驗

陳甜甜， 李道靖， 張素燕， 劉 爭， 楊毅青

(1.北京航空航天大學 機械工程及自動化學院，北京 100191； 2.首都航天機械有限公司，北京 100076)

薄壁零件被廣泛應用于航空航天領域，對其加工精度和表面質量要求極高。由于薄壁件剛性差，切削動力學特性隨著加工過程快速變化，導致薄壁件切削穩定性多變，極易發生顫振，難以達到加工要求，極大的影響刀具壽命和加工效率[1]。為了抑制薄壁件在加工中的振動，主要采用工藝優化、主動抑振技術和被動抑振技術等。被動抑振技術具有實施方便、效果明顯等優點，在切削加工過程中被普遍采用，其主要可分為動力吸振和耗能減振。

動力吸振方式形式多樣，主要以調諧質量阻尼器為代表，其中單自由度吸振器因其結構簡單、抑振效果明顯的優點被廣泛采用。為使動力吸振器在質量不變的情況下發揮最佳的抑振效果，要對其剛度、阻尼等參數進行優化，國內外學者在這個方向做了大量研究，提出了一系列的優化準則和優化算法。Den Hartog[2]以抑制主結構振幅為目標，利用“不動點”理論，推導出主結構無阻尼情況下單自由度阻尼器H∞準則的解析解，Crandall[3]以主系統幅頻特性曲線與頻率軸圍成面積最小為目標提出了H2優化準則，Moradi[4]選取了多組銑削參數，以刀具振動最小化為目的對阻尼器位置與剛度優化進行研究。單自由度動力吸振器性能優越，抑振效果明顯，然而其對頻率匹配要求高，只能抑制某一特定模態振動。針對多模態振動抑制的多自由度動力吸振器結構設計和參數優化較為復雜，無法很好的適應薄壁零件切削時出現的多階振動模態和動力學特性快速多變的特點[5-6]。

耗能減振通過增加結構阻尼，利用相對運動耗散振動能量，起到減小振動的作用。根據作用原理可將其分為黏彈性阻尼技術、電渦流阻尼技術、摩擦阻尼技術、沖擊阻尼技術和黏滯性阻尼技術。Kolluru等[7]提出了在工件表層粘貼薄柔性層與質量塊的阻尼減振方案。Shi等[8]設計了一種附著于薄壁零件上的黏彈性阻尼器并成功應用于銑削加工振動抑制。Yang等[9]設計了一種可調剛度電渦流阻尼器，旨在抑制薄壁零件銑削加工中工件的振動。Ziegert等[10]基于庫侖摩擦理論提出了一種指狀摩擦減振銑刀，并從理論和實驗方面論證了該銑刀對高頻振動的抑制效果。Yang等[11]基于沖擊理論，結合懸臂梁模型設計了一種沖擊阻尼器，并將其成功運用到車刀上。Gubanov[12]基于空氣黏滯阻尼效應設計了一種耗能阻尼器，對加工振動抑振效果明顯。耗能減振通過提高系統阻尼抑制系統振動，相較于動力吸振方式，其抑振效果受目標模態動力學參數變化的影響較小，因此適合具備多階弱剛性模態的薄壁件切削振動抑制。

綜合以上，針對薄壁零件切削過程中動力學特性多變的特點以及動力吸振器適應性不足等問題，本文擬研究基于黏滯阻尼原理的被動阻尼減振技術，設計一種被動阻尼器，通過理論建模得出阻尼系數與流體動力黏度以及結構參數之間的關系，以空氣介質為例，通過模態測試和激振試驗對其阻尼特性進行測試。

1 理論建模

1.1 運動方程推導

基于耗能減振原理的被動阻尼器其模型如圖1所示，通過增加主結構的阻尼起到抑振效果，其中，k1、c1、m1分別為主系統的剛度、阻尼和質量，m2和c2分別為阻尼器質量和阻尼。

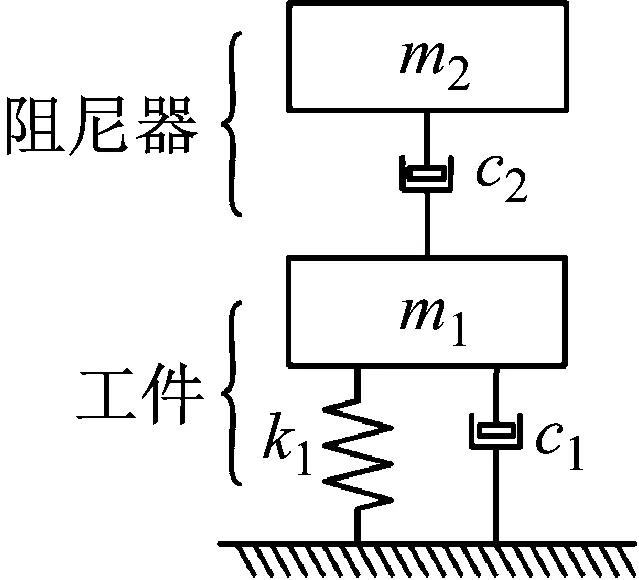
圖1 耗能阻尼器動力學模型

其動力學方程如下

H(ω)=

(1)

假設主系統阻尼c1為零，對式(1)進行無量綱化，可得：

(2)

式中相應參數可表示為

式中：μ為阻尼器與主系統的質量比；ω0為主系統固有角頻率；Ω為無量綱化的角頻率。

則無量綱頻響函數實部G(Ω)為

(3)

根據銑削顫振理論[13]，臨界穩態切深為

(4)

式中：aplim為臨界穩態切深；Kt為切向力系數；Z為銑刀齒數；β0為方向系數平均值；Gmin為頻響函數實部最小值。由式(4)可知，在加工條件一定時，頻響函數實部最小值與穩態切深呈負相關。

根據Sims的不動點理論[14]，式(3)存在三個不動點

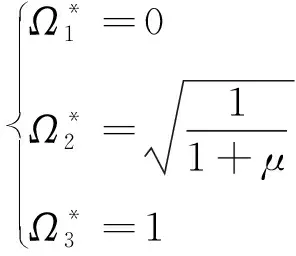
(5)

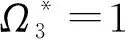
(6)

所以，阻尼器的最佳阻尼系數c2opt取值為

(7)

取μ=1，在不同c2對G(Ω)進行仿真，結果如圖2所示。

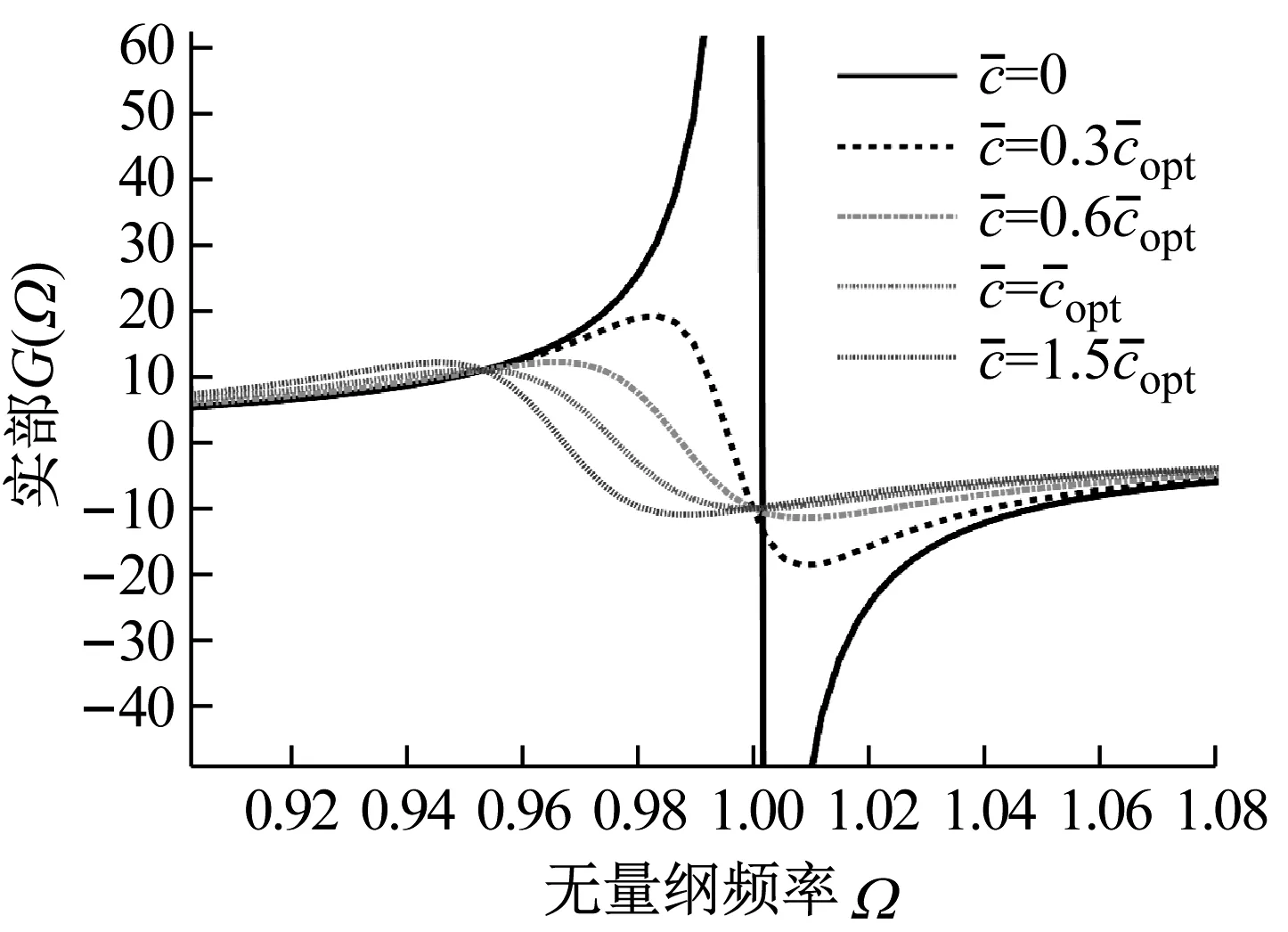
圖2 G(Ω)仿真

由圖2可知，在阻尼器阻尼系數c2小于其最優阻尼系數c2opt時，隨著阻尼器阻尼c2的增大，頻響函數最小負實部增大，系統穩定性提高；當c2達到最優阻尼系數c2opt時，頻響函數最小負實部達到最大值；當c2超過最優阻尼系數c2opt時，頻響函數最小負實部隨著c2增大而減小，系統穩定性降低。因此，對于一個給定的系統來說，當阻尼器阻尼系數c2為最佳阻尼系數c2opt時，系統穩定性最好。

1.2 黏滯阻尼原理

在流體流過圓環縫隙時，如圖3所示，由于流體具有黏度，所以其會提供一個黏性力Ff，當圓環縫隙的外殼與內部發生相對運動時，這個黏性力Ff會阻礙這個相對運動，即對運動提供了一定的阻尼。基于此原理，設計一種被動阻尼器如圖4所示。

圖3 環狀縫隙

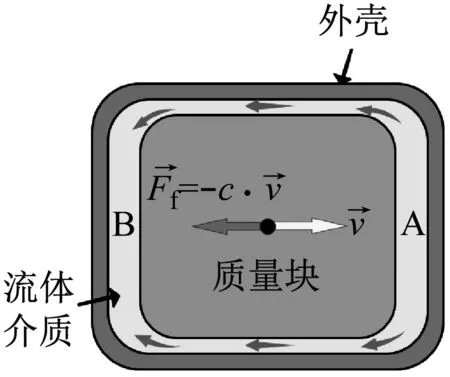
圖4 阻尼器結構

阻尼器由圓柱體外殼、質量塊以及內部均勻填充的流體介質組成。在外殼與質量塊間留有一定的徑向間隙g，當阻尼器隨工件一起振動時，內部質量塊會沿軸向運動。當內部質量塊相對外殼以如圖4所示速度運動時時，會對A處介質產生擠壓，迫使該處介質沿著徑向間隙g流向B處，在這個過程中由于流體介質具有黏性，因此會提供一個作用力Ff，該力會阻礙質量塊的軸向運動且會將質量塊動能的一部分轉化為熱能耗散，從而耗散振動能量，起到抑振的效果。

由流體的縫隙流動相關理論可知[15]，流體在圓環形縫隙中流動時，其流量Q可由下式推出

(8)

式中：h為縫隙寬度；a為環狀縫隙截面周長；μa為流體動力黏度；L為環狀縫隙軸向長度；ΔP為縫隙前后兩側壓強差。

對于環狀縫隙來說，由于其縫隙寬度h較小，因此其可以等效看作平板縫隙流動，即其截面周長為

a=πD

(9)

式中，D為質量塊直徑。縫隙長度L與質量塊長度l相等，即:

L=l

(10)

縫隙寬度為徑向間隙g的一半，即：

(11)

假設質量塊與外殼之間的相對運動速度為v，則流體在縫隙中的流動速度也為v，則流過縫隙的流體流量Q為

(12)

質量塊兩側壓強差給予質量塊的阻力Ff為

Ff=ΔPSd

(13)

因此，可以求出阻尼器的阻尼系數為

(14)

由式(14)可知阻尼器的阻尼系數與流體介質的動力黏度μa和質量塊與外殼之間的徑向間隙g有關。其與流體動力黏度大小成正比，與徑向間隙的三次方成反比，因此從理論上流體的動力黏度越大，質量塊與外殼之間的徑向間隙越小，阻尼器所具有的阻尼系數越大。

結合式(7)與式(14)，可知在選定流體介質后，即可計算出阻尼器徑向間隙g

(15)

2 結構設計

傳統阻尼器裝夾通常使用粘貼或螺栓緊固的方式，其會對工件表面造成一定影響，因此選擇真空吸附的方式對阻尼器進行安裝和固定。選擇的真空吸盤型號為SMC公司型號的ZP2-TB20MTN-H5，轉接頭通過兩個正交孔形成通氣回路，使吸盤與工件表面間的空氣可由該回路被真空泵抽出，從而形成負壓，使裝置能夠牢固的固定在工件表面。為盡量減少零件個數，使整個裝置更加簡潔可靠，使用轉接頭的端面代替阻尼器端蓋。真空轉接頭如圖5所示。

(a) 三維模型

依據1.2節黏滯阻尼原理，設計的阻尼器結構如圖6所示，其由外殼與內部質量塊組成，內部質量塊質量與工件模態質量相同，質量塊與外殼的徑向間隙由式(15)計算得出，內部流體介質選擇空氣。

(a) 三維模型圖

3 模態測試

設計圓筒鋁合金薄壁框(直徑300 mm，高80 mm，壁厚8 mm)作為抑振對象，通過模態試驗和激振試驗測試本文所述阻尼器效果。

采用模態試驗測試本文所述阻尼器的阻尼特性。試驗設備如表1所示。

表1 模態測試試驗設備

測試對象采用三角定位安裝方式，分別于Ⅰ、Ⅱ、Ⅲ三個位置進行壓緊固定，其上被等間距劃分為1～6六個位置，分別對這六個位置的頻響函數進行測試。模態測試安裝如圖7所示。

(a) 工件安裝及測試區域

對工件進行交叉點頻響函數模態測試，測試時力錘敲擊點與阻尼器安裝點保持在位置1不變，加速度計分別安裝在1～6各區域并測試該點頻響函數。測試結果如圖8所示。

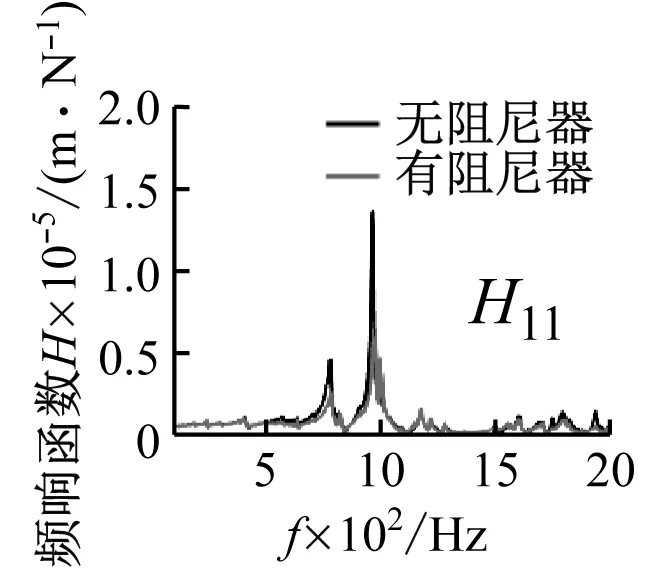
(a) 各位置頻響函數幅值

由圖8(a)可以看出，在安裝阻尼器后，1～6各位置振動模態峰值均有明顯下降，最高可使振動模態峰值下降約60%。由圖8(b)可知，在安裝阻尼器后，各位置頻響函數最小實部均有明顯提高，說明在安裝阻尼器后，系統穩定性具有明顯提升。

對模態測試得到的頻響函數進行參數辨識，在未安裝阻尼器時零件阻尼比為0.403%，通過仿真，所設計的阻尼器理論上應能使零件阻尼比達到0.943%，實際測試中安裝阻尼器后的零件阻尼比平均達到了0.876%，由此可以看出，阻尼器實際達到的阻尼參數與設計參數較為接近。

通過模態測試得到零件安裝阻尼器前后的頻響函數，并將其導入Cutpro軟件中進行銑削顫振穩定域圖仿真。材料為鋁合金7075，其切向切削力系數Ktc為897.48 N/mm2，徑向力系數Krc為205.95 N/mm2，在4齒圓柱銑刀槽銑條件下繪制銑削加工穩定域圖，如圖9所示。從圖中可以看出，在安裝阻尼器后，最小臨界切深提高了約2.08倍，說明本文所提出的被動抑制振動技術能在銑削過程中發揮較好的效果。

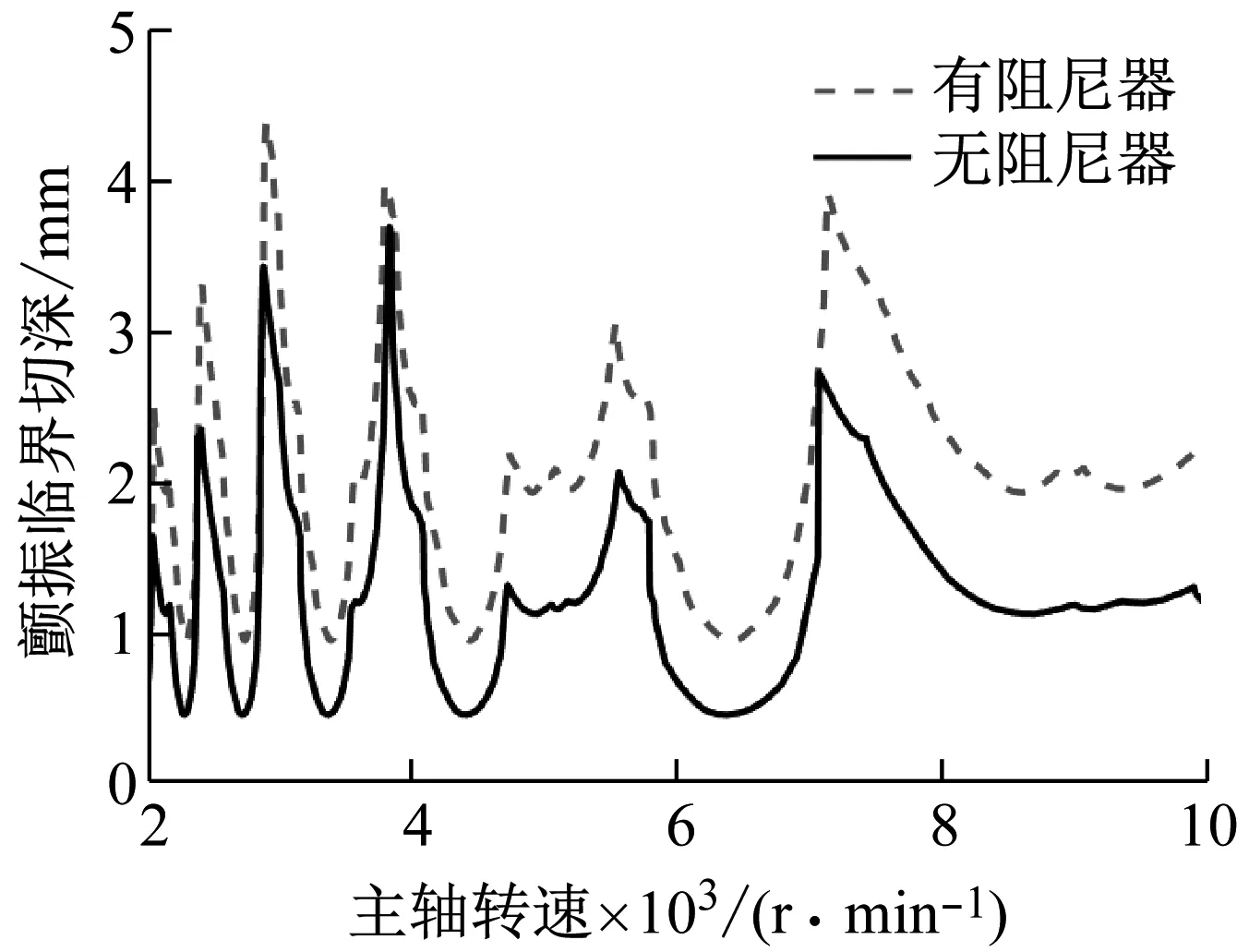
圖9 顫振穩定域預測圖

4 激振試驗

對所述工件進行激振試驗，檢測所設計阻尼器在外界連續激勵振動條件下抑振效果。激振器選擇HEV-20電磁激振器。

在工件安裝后，首先使用掃頻確定工件安裝后的共振峰頻率，然后在共振頻率處對工件進行激振，測試阻尼器的抑振效果。激振試驗各裝置安裝情況如圖10所示。

圖10 激振試驗

由模態測試結果可知，所述工件在圖10所示安裝環境下共振峰在1 000 Hz附近，通過激振器對頻率范圍50～2 000 Hz掃頻得出工件的振動幅值如圖11所示。

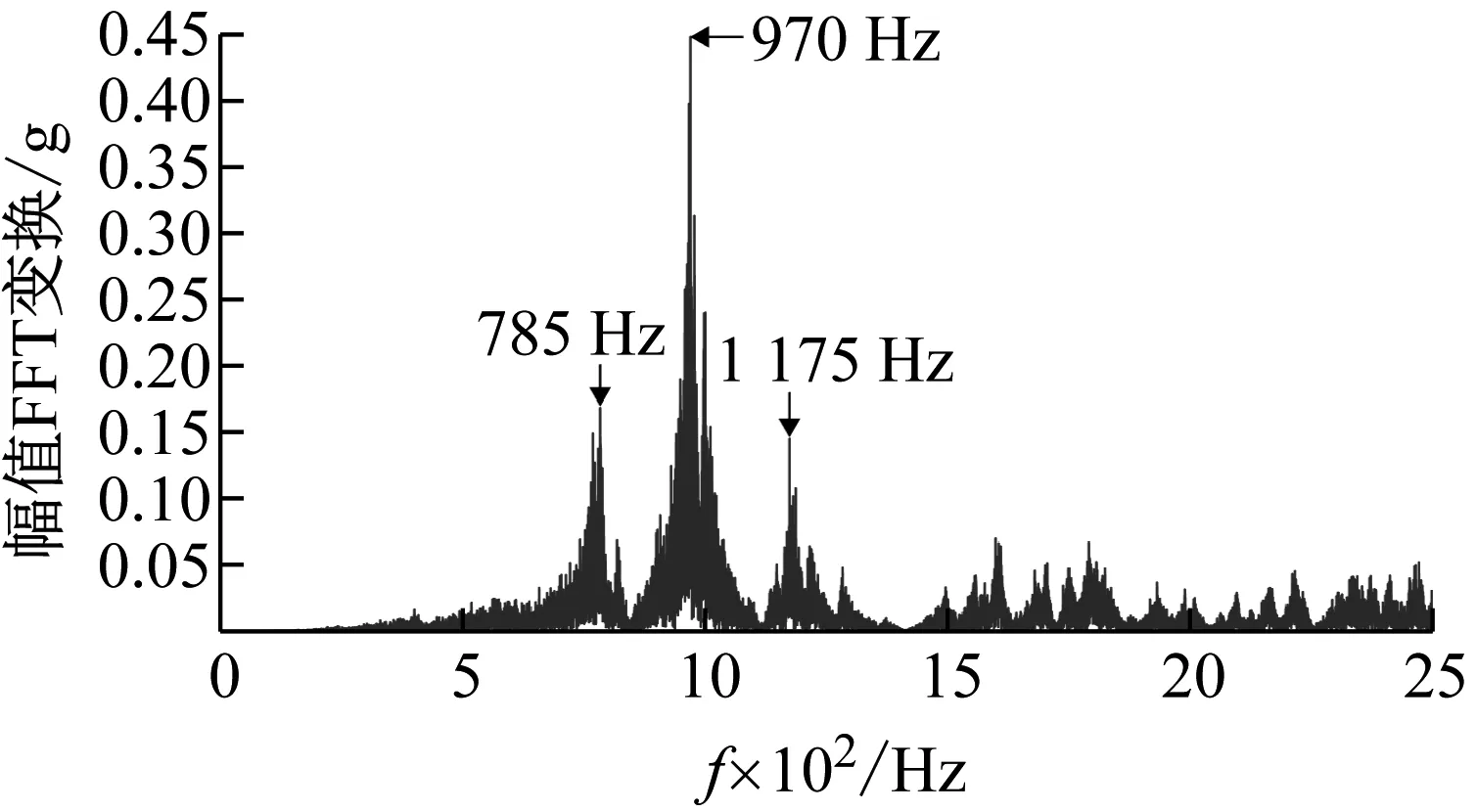
圖11 50～2 000 Hz正弦掃頻時的工件響應

由圖11可知，在圖10所示安裝情況下，工件共有三個較為強烈的共振峰，分別為785 Hz、970 Hz和1 175 Hz。將阻尼器與加速度計固定在點1處，用激振器分別在這三個頻率下對1～6點進行激振，測得安裝阻尼器前后工件加速度對比如圖12所示。

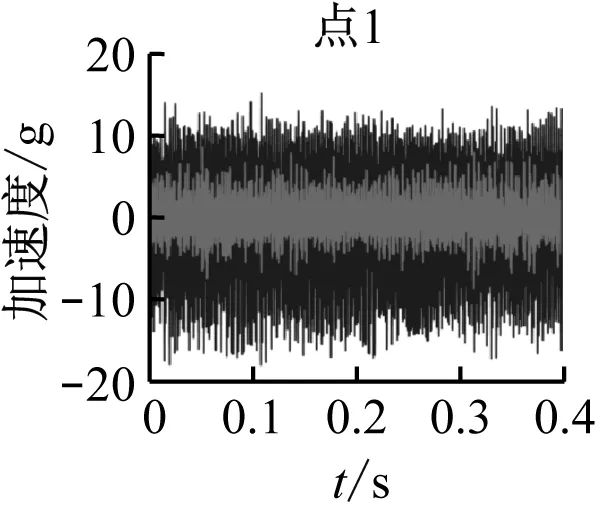
(a) 785 Hz正弦激勵

由圖12可以看出，在安裝阻尼器后對工件振動具有明顯的削弱作用，對掃頻試驗中振動較為明顯的三個頻率785 Hz、970 Hz和1 175 Hz，安裝阻尼器后工件加速度分別平均降低了58%、60%和63%，且安裝阻尼器后工件振動更為穩定，因此可知所述阻尼器能夠有效的抑制工件振動。

5 結 論

薄壁件自身剛性差，切削加工過程中易發生振動。本文設計了基于黏滯阻尼原理的被動阻尼器，其通過真空吸附的方式吸附在圓筒薄壁零件上。在切削過程中，阻尼器將零件的動能轉移到質量塊上，并通過空氣的黏滯阻尼進行耗散，從而起到抑制薄壁件振動的作用，抑制效果明顯，針對薄壁件復雜加工過程具有較強的適應性。結論如下：

(1) 針對圓筒薄壁件的模態測試結果表明，所設計的基于流體黏滯阻尼原理的被動阻尼器具有良好的抑振效果，振動模態幅值最大可降低約60%。

(2) 將該阻尼器應用于圓筒薄壁件激振試驗時，可明顯降低工件振動幅值，激振試驗表明薄壁圓筒零件振動加速度下降36%～67%，具有明顯抑振效果。

(3) 安裝阻尼器后，系統阻尼比從0.403%平均提升至0.876%，提升了約2.17倍，最小臨界切深提升了約2.08倍。